Roberto Renzetti
IL PRINCIPIO DI INDETERMINAZIONE (HEISENBERG 1926/1927)
Nelle cose che siamo andati dicendo, a partire da De Broglie, già era sparita la particella materiale. Occorreva dirlo meglio. Formalizzare. E per questo Heisenberg ebbe delle straordinarie intuizioni che poi purtroppo vennero estrapolate arbitrariamente fino a creare gravi problemi di interpretazione filosofica della meccanica quantistica. Intanto Heisenberg fa una operazione che rivoluziona il modo di osservare; egli non guarda più dall’esterno ma si mette dentro ciò che vuole osservare (non è una cosa da poco!).
Cerchiamo di capire cosa è tale principio di indeterminazione.
Quando vogliamo descrivere che farà un proiettile sparato da un cannone, non occorre che ci mettiamo ad osservare per credere che le cose vadano in un certo modo. Due calcoletti con la fisica di Newton e riusciamo a conoscere, istante per istante, la traiettoria (o velocità) e la posizione del proiettile. La cosa assume una rilevanza diversa nel mondo microscopico, dove i fenomeni vanno trattati con i quanti.
Occorre prima dire in breve il modo in cui noi vediamo gli oggetti, modo simile sia nella visione ordinaria che quantistica della luce. Dato un oggetto da osservare serve una sorgente di luce che, dopo essersi riflessa sull’oggetto da osservare, arriva agli occhi dell’osservatore informandolo che l’oggetto è proprio lì (si noti che questo toccare indiretto degli oggetti per vederli, corrisponde al toccare diretto del non vedente che si aggira in un ambiente che non conosce).
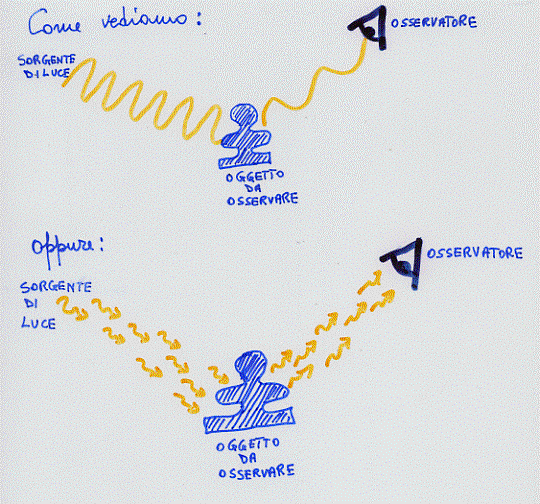
fig. 29
Riferiamoci a dei fotoni che debbano colpire un oggetto perché noi lo si possa vedere (secondo disegno). Le energie in gioco, quelle dei fotoni che colpiscono l’oggetto sono veramente ridicole rispetto all’inerzia dell’oggetto. Possiamo anche prendere un faro usato dalla protezione civile per le inondazioni ed illuminare con esso un granello di sabbia. Tale granello non si sposterà perché colpito da quell’enorme fascio di fotoni. E’ che il granello di sabbia è immensamente più grande del mondo atomico. Scendiamo allora a tale scala. Se volessimo osservare un elettrone dovremmo vederlo. Per fare ciò occorre che almeno un fotone lo colpisca. Ebbene, l’energia di un fotone è dello stesso ordine di grandezza di quella di un elettrone! Ciò vuol dire che, se vogliamo osservare l’elettrone, lo vediamo per un istante infinitesimo, ma poi lo perdiamo perché l’urto del fotone lo ha fatto schizzare via (si riveda l’effetto Compton). Quindi si potrebbe pensare di osservare la posizione di un elettrone ma, questa osservazione, ci toglie ogni possibile informazione su quale traiettoria è seguita da quell’elettrone. Ma si potrebbero usare fotoni meno energetici. Invece di quelli, ad esempio, viola, si possono usare quelli rossi. Benissimo. In tal caso non spostiamo apprezzabilmente l’elettrone dalla sua traiettoria ma non riusciamo a vederlo bene, lo vediamo sfocato. Se ci mettiamo con fotoni ad energia intermedia (verdi) perdiamo un poco di informazione sulla traiettoria e poca sulla posizione dell’elettrone.
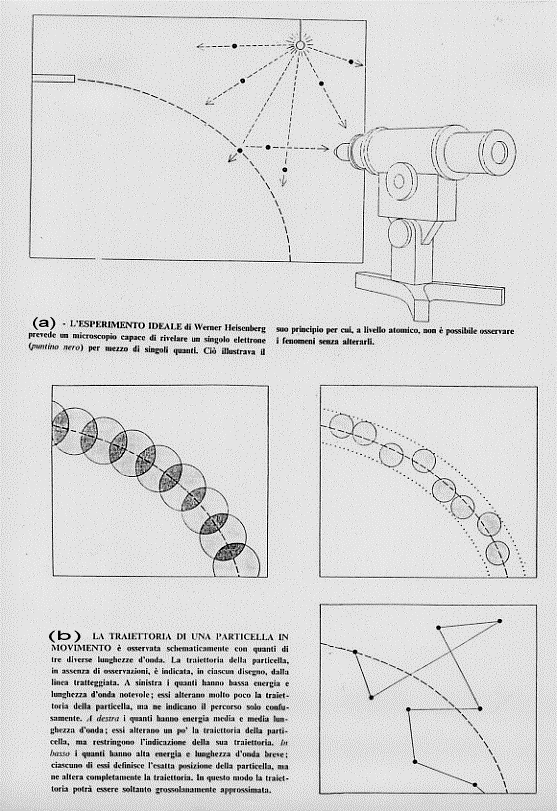
fig. 30
In formula il principio di indeterminazione si scrive:
Δvx . Δvy . Δvz . Δx . Δy . Δz ≥ h/2πm
e qui occorrerebbe discutere di questo spazio a sei dimensioni che si è introdotto, lo spazio delle fasi, ma ci limitiamo solo a considerare il principio di indeterminazione in una dimensione, così il tutto si semplifica:
Δvx . Δx . ≥ h/2πm
dove la formula dice che il prodotto dell’indeterminazione sulla traiettoria (o velocità) per l’indeterminazione sulla posizione non può essere inferiore a quella quantità scritta al secondo membro. Facendo dei conticini facili (si veda ‘atomi e molecole’ al paragrafo “Principio di indeterminazione”) si trova che l’indeterminazione della posizione dell’elettrone in un atomo è ora grande come tutto l’atomo e ciò vuol dire che spariscono orbite e triettorie e la stessa individualità dell’elettone. Ora quest’ultimo può trovarsi dovunque dentro l’atomo ma non sappiamo dove e neppure come si muove.
Conoscere vuol dire misurare, misurare vuol dire perturbare e perturbare ci porta ad essere indeterminati nel mondo microscopico (noto a parte che nell’esperimento ideale di Heisenberg, descritto dalla figura 30, gli strumenti sono classici e non quantistici e qui si apre un altro fronte non secondario di discussione che rimandiamo oltre). Secondo il fisico russo (espatriato in USA) Gamow in un mondo quantistico non si potrebbe accarezzare un gattino senza spezzargli il collo, tali sono le cose straordinarie che accadono e che non rispondono a quello che conosciamo come senso comune. Il principio di indeterminazione, il carattere probabilistico della fisica dei quanti ed il dualismo onda-corpuscolo non sono altro che espressioni diverse di un solo modo, assai complesso, di rappresentare il mondo microscopico esterno. Si è voluto estendere a tutta la realtà del mondo questo principio con affermazioni che implicherebbero il dover abbandonare le nostre libertà metafisiche ed anche su questo torneremo oltre.
IL PRINCIPIO DI COMPLEMENTARITA’ (BOHR 1927)
Tale principio fu enunciato da Bohr in un convegno che si tenne a Como nel 1927. Dico questo perché, avrete letto, la fisica italiana brillava per la sua assenza nell’elaborazione della fisica dei quanti. I lavori di Fermi e del suo gruppo crearono però un tale prestigio intorno alla nostra fisica che scienziati di prim’ordine iniziarono ad avvicinarsi al nostro Paese.
Secondo Bohr, ogni esperienza capace di evidenziare una particella da un punto di vista corpuscolare esclude la possibilità di determinare il suo aspetto ondulatorio. In fisica quantistica niente impedisce di localizzare un elettrone ma, una volta localizzato, esso è determinato come particella. Se vogliamo invece misurare la lunghezza d’onda di un elettrone, ad esempio mediante diffrazione, dobbiamo concludere che l’elettrone è un’onda. Secondo Bohr, onda e particella non sono più concetti incompatibili ma dipendono dai risultati delle misure e dalla strumentazione utilizzata. Il dualismo onda-corpuscolo di materia e radiazione diventa, per Bohr, la complementarità dei due aspetti:
se un esperimento permette di osservare un aspetto di un fenomeno fisico, esso impedisce, al tempo stesso di osservare l’aspetto complementare dello stesso fenomeno.
Quindi il punto di vista “quantistico” è più radicale del pragmatismo dei positivisti logici, i quali sosterrebbero che è senza significato parlare di grandezze che non possono essere misurate. La complementarità asserisce che non è solo privo di significato affermare di conoscere simultaneamente gli esatti valori di velocità e posizione: queste grandezze non esistono!!! E fu proprio Bohr ad elevare il concetto di complementarità a significato filosofico più ampio. Coppie complementari erano: libero arbitrio e determinismo, vitalismo e meccanicismo, causalità e spazio-tempo, vita e descrizione scientifica, ……. (in alcune delle coppie riportate si sente l’influsso delle convinzioni del padre di Bohr, che era un fisiologo).
In definitiva risulta che le leggi della meccanica quantistica, esattamente deterministiche, governano un substrato del mondo che non è per noi direttamente accessibile perché inosservabile. Ciò che è invece osservabile può essere predetto solo probabilisticamente. Al crescere degli oggetti presi in considerazione, le relative lunghezze d’onda di De Broglie diventano più piccole, essi sono più localizzati intorno al valor medio e quindi sono descritti con accuratezza crescente dalla meccanica classica, cosicché i valori medi delle osservazioni quantistiche risultano obbedire alle leggi classiche del moto.
LA CONDUZIONE (Block 1928; Kronig e Penney 1930)
Uno dei fenomeni che non aveva trovato alcuna spiegazione con la fisica “classica” era relativo alla conduzione elettrica:
– al crescere della temperatura un conduttore conduce sempre meno;
– al crescere della temperatura un isolante conduce sempre più.
Vi è poi una questione di fondo:
– perché un materiale conduce elettricità ed un altro no?
Mediante i quanti venne sviluppata la teoria delle bande di energia (una sorta di estensione dell’atomo di Bohr ad un intero cristallo – si veda l’articolo relativo nel sito) con la quale emersero con chiarezza spiegazioni alle due questioni suddette. Ma non basta. La teoria era particolarmente buona perché, oltre a spiegare, dava previsioni e, in particolare, quella di materiali semiconduttori.
LA FISICA NUCLEARE
Nel 1932 iniziò l’impetuoso sviluppo della fisica nucleare (con determinanti contributi di Fermi e della Scuola di Roma in cui ebbero un ruolo fondamentale Amaldi e Rasetti, contrariamente a quanto dice l’ignorante Zichichi). Tale sviluppo sarebbe stato impossibile senza la fisica dei quanti (si veda l’articolo su Fermi e la Scuola di Roma nel sito).
EFFETTO TUNNEL (Wilson 1932)
Tale fenomeno ha luogo in: particolari semiconduttori, transistor, lamine superconduttrici, microscopia elettronica,…… Tento una rapida descrizione del fenomeno.
Supponiamo di avere un recipiente contenitore (bicchiere, tazza, …) ed una pallina. Secondo la visione classica si possono avere solo i due casi di figura 31.
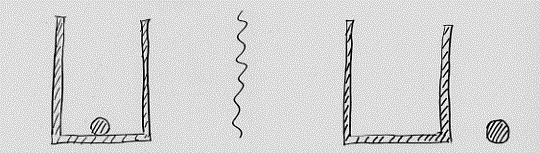
fig. 31
– nel primo caso la pallina è dentro il contenitore;
– nel secondo caso la pallina è fuori il contenitore.
Secondo la visione quantistica, la “barriera” rappresentata dalle pareti del contenitore diventa una barriera di potenziale che ha una qualche probabilità di essere perforata (tunnel):
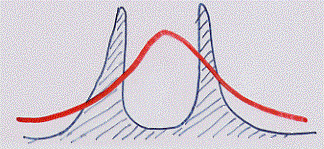
fig. 32
La barriera in nero è una barriera di energia mentre la curva in rosso rappresenta la probabilità di trovare la pallina in un dato luogo. Riferendoci al secondo caso visto precedentemente, la massima probabilità di trovare la pallina è ora dentro la buca di energia ma vi è una probabilità non nulla di averla fuori. La pallina è simultaneamente dentro e fuori. Una volta localizzata sparisce la curva di probabilità (principio di complementarità) e se la trovassimo fuori dalla barriera è come se avesse attraversato un tunnel:
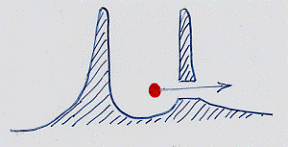
fig. 33
A parte ogni altra considerazione, nasce un problema legato ai tempi di transito attraverso la barriera: la pallina/particella che attraversa la barriera sembra farlo in tempi inferiori a quello che impiegherebbe una particella che non deve attraversare alcuna barriera. Sembrerebbe che si abbia a che fare con un viaggio indietro nel tempo (e le fluttuazioni, a livello macroscopico, non escludono un tale evento – vedi l’Appendice alla Relatività su Le fluttuazioni -). Si viola la relatività? Il discorso sarebbe complesso ed esula da quanto mi sono proposto. Ma chi fosse interessato può trovare una discussione del problema in David Bohm, Wholeness and the implicate order, Routledge & Keagan Paul Ltd 1980 oppure, in modo più semplice, in A. M. Steinberg, P. G. Kwait e R. Y. Chiao in Più veloce della luce ? – Le Scienze n° 302, Ottobre 1993 (pagg. 20-28). In ogni caso, tornare indietro nel tempo significherebbe andare a velocità superiori a quelle della luce. Il fatto è che tali velocità non sono mai state misurate e, finché non lo saranno, non vi è alcuna violazione della Relatività. E’ comunque di interesse riportare due illustrazioni dall’articolo di Le Scienze citato:

fig. 34
In questa figura si vede Alice (nel Paese delle meraviglie di Lewis Carrol) che colpisce dei porcospini con un fenicottero, mandandoli ad urtare contro un muro. I porcospini hanno il viso di Heisenberg. Uno di essi attraversa la barriera e resta stupito osservando il suo orologio di fronte all’altro personaggio stupito, coniglio-Einstein.

fig. 35
In quest’altra figura è rappresentato proprio il momento del passaggio di Alice al di là dello specchio. Si noti che l’orologio è “attivo” mentre Alice è ancora “al di qua”, mentre diventa una sorta di clown quando Alice è passata “al di là”.
ANCORA INTERFERENZA
Una attenta discussione dell’interferenza delle particelle porta a considerare un paradosso.
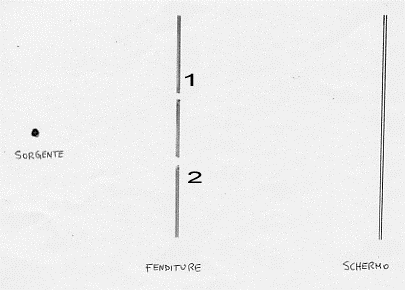
fig.36
Supponiamo di ridurre l’intensità della sorgente in modo che un solo fotone per volta passi attraverso le fenditure (più corretto sembrerebbe il dire la fenditura). Dopo un certo tempo, sullo schermo, si ridisegna la classica figura di interferenza (zone chiare alternate a zone buie). Il paradosso sta nel fatto che ciascun fotone potrà passare solo attraverso una fenditura e non va ad interferire con nessun altro fotone: eppure dopo un poco di tempo c’è interferenza sullo schermo. Un fotone singolo scegliendo una fenditura obbedisce ad una legge statistica conveniente che si realizza solo se esso sa se l’altra fenditura è aperta o chiusa. E’ l’interferenza tra probabilità che origina la figura sullo schermo.
Si supponga ora che vi siano solo due possibilità:
– la particella passa per la fenditura 1 (Universo A)
– la particella passa per la fenditura 2 (universo B).
Ciascuna di queste due possibilità è, secondo Bohr, rappresentativa di un Universo differente. In un mondo la particella passa per la fenditura 1; in un altro mondo essa passa per la fenditura 2. Il mondo reale, quello dell’esperienza, è un mondo completamente diverso da questi mondi semplici. Il mondo reale è un miscuglio di ibrido di questi due mondi semplici possibili ed ogni mondo interferisce con l’altro. Se si potesse osservare attraverso quale fenditura passa la particella si eliminerebbe un mondo scegliendone uno solo: la particella risulterebbe localizzata, non vi sarebbe più interferenza. La situazione dell’esperienza è quindi descritta dalla sovrapposizione di due stati: particella in 1 che rappresentiamo così |P1> e particella in 2 che rappresentiamo allo stesso modo |P2>. Tale sovrapposizione è la funzione d’onda Ψ (t) che avrà la seguente forma (0,707 |A> è un fattore di normalizzazione):
|Ψ (t) > ~ 0,707 |A> ( |P1> + |P2> ).
E’ la nostra osservazione che, eventualmente, elimina una possibilità e quindi l’interferenza (riducendo di conseguenza la funzione d’onda).
E’ facile rendersi conto che nascono molti problemi su cosa sia la realtà ed addirittura il problema dell’esistenza della realtà. La questione venne fuori in tutta la sua drammaticità nel Congresso Solvay di Copenaghen (1927). Lì si scontrarono due schieramenti di fisici:
– Bohr, Born, Heisenberg, Dirac, Pauli, Jordan (la cosiddetta Scuola di Copenaghen);
– Einstein, De Broglie, Schrödinger, Planck, Erenfest, Lorentz, Laue.
Le questioni sul tappeto sono riassumibili in una domanda di base:
esiste una realtà indipendentemente dalle nostre osservazioni?
A tale domanda le risposte possibili sono almeno tre:
1) SI (punto di vista realista o metafisico-ontologico)
2) NO (punto di vista idealista)
3) LA QUESTIONE NON HA SENSO (punto di vista agnostico o operativista).
La fisica newtoniana è consistente con tutti e tre i punti di vista ora accennati. Non obbliga ad un punto di vista particolare. E ciò non significa che la fisica è più generale della metafisica ma solo che la fisica dei quanti impone una scelta tra i tre punti di vista limitando le nostre libertà metafisiche. La Scuola di Copenaghen scelse il 3° punto di vista: accettò come fondamentale il concetto di quanto, bandì dalla teoria tutte le grandezze non osservabili e rinunciò al determinismo. Le leggi probabilistiche della fisica dei quanti furono considerate come una realtà definitiva ed il principio di Heisenberg fu assunto a prova di un determinismo fondamentale nelle leggi della natura.
Ma si andò anche oltre.
Non ci si limitò a dire che non è possibile conoscere simultaneamente posizione e velocità di una particella; si affermò addirittura che in generale una particella non ha né una posizione né una velocità ben determinate. La particella è diffusa in tutta l’onda e quindi si trova, con maggiore o minore probabilità, contemporaneamente in tutta l’onda. La particella ha contemporaneamente, con diverse probabilità, diverse velocità.
Gli altri furono sconfitti. Fu soprattutto Einstein che per anni tentò di ribattere e di portare argomenti a sostegno delle tesi opposte a quelle che vinsero.
Ma vediamo in modo didascalico le differenze esistenti tra le varie interpretazioni della fisica quantistica riferendoci ai vari punti di vista cui abbiamo accennato.
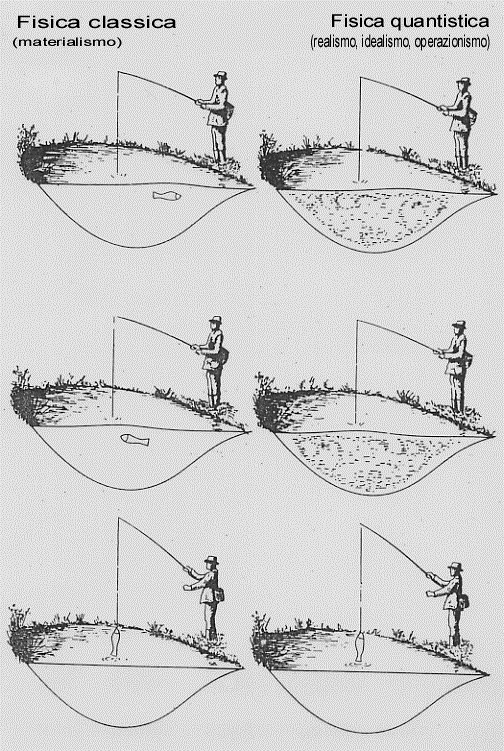
fig. 37.
La prima colonna di fig. 37 raffigura un pescatore che ha a che fare con un mondo classico, mondo che diventa quantistico nella seconda colonna. Nella fig. 38 si hanno diverse interpretazioni quantistiche del mondo quantistico.
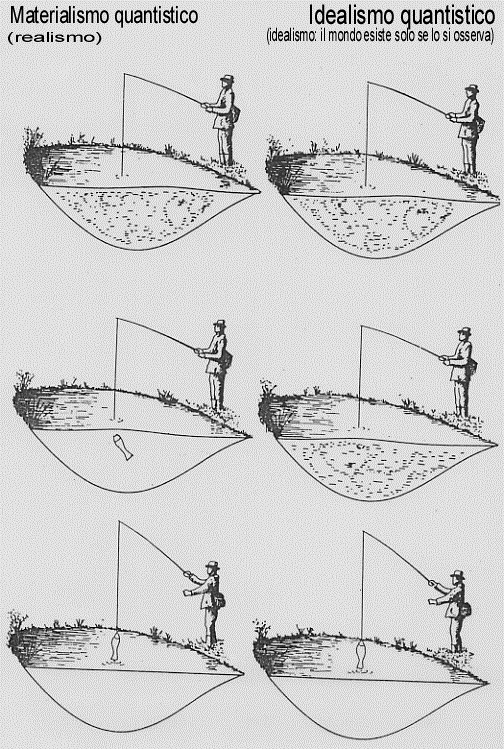
fig. 38
E qui ancora si discute ….. Il punto di vista operazionista prevede invece che queste discussioni fanno perdere tempo (si tratta del portato diretto dell’efficientismo nel mondo della ricerca scientifica). E si potrebbe continuare. Se il pescatore rigetta il pesce in acqua esso ritorna ad essere indeterminato. Ed accade anche che due pesci, due eventi, rigettati in acqua, originano un solo evento indeterminato (fig. 39).
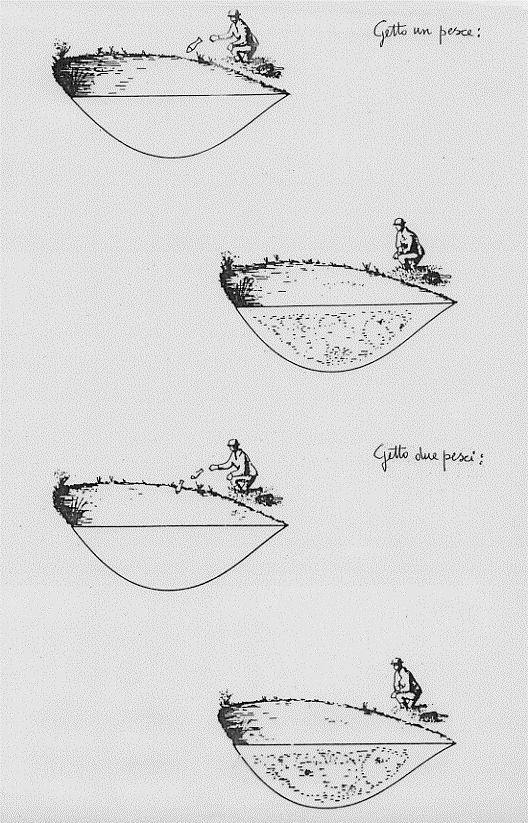
fig. 39
Ma vediamo le cose come furono presentate da alcuni fisici di primo piano.
IL GATTO DI SCHRÖDINGER (1935)
Un gatto viene posto in una scatola chiusa ed isolata visivamente ed acusticamente. Dentro la scatola vi è un fucile con un meccanismo di sparo automatico attivato da fotoni che entrano in O.
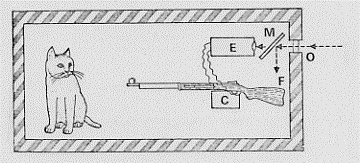
fig. 40
Tali fotoni, a seguito dello specchio semitrasprente M, possono al 50% far sparare il fucile o no. Dopo, diciamo, qualche minuto possiamo chiederci se il gatto è vivo |G.V.> o se il gatto è morto |G.M.>. Il punto di vista realista ci farebbe dire:
“il gatto o è vivo o è morto quando non lo osserviamo”.
La fisica dei quanti ci dice invece che il gatto è simultaneamente vivo e morto. E’ la nostra curiosità, la voglia di aprire la scatola e di vedere che, eventualmente, lo uccide. La funzione d’onda che descrive il sistema è una sovrapposizione di gatto vivo e gatto morto:
|Ψ (t) > ~ 0,707 |A> ( |G.V.> + |G.M.> ).
Per superare la difficoltà bisogna rinunciare all’assunto metafisico che il gatto o è vivo o è morto. Da questo punto di vista occorrerebbe dire o che il gatto non esiste quando non è osservato o che la questione della sua esistenza non può essere posta. Come si vede e come annunciato, la fisica quantistica limita la nostra libertà metafisica.
IL PARADOSSO EINSTEIN – PODOLSKY – ROSEN (EPR 1935)
Di tale paradosso esistono varie versioni. Vediamone un paio. Supponiamo di disporre di una particella (che abbia spin uguale a zero) che decada in due particelle che si muovono in direzioni opposte alla stessa velocità in modulo (nell’esempio fatto in fig. 41 abbiamo un pione positivo che si disintegra in un muone positivo ed in un neutrino muonico):
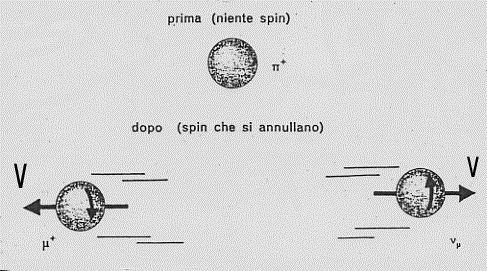
fig. 41
Se, dopo un certo tempo, misuriamo la posizione di una delle due particelle con una qualche precisione, abbiamo determinato anche la posizione della seconda che deve trovarsi alla stessa distanza dalla sorgente. Oppure si potrebbe decidere di misurare la traiettoria di una delle due, ricavando immediatamente quella della seconda. Perciò, secondo EPR, se, eseguendo una misura sulla particella 1, posso determinare con una precisione a piacere la posizione della particella 2 (senza operare direttamente su di essa) devo concludere che la posizione della particella 2 è un elemento di realtà fisica che posso accertare senza disturbare la particella stessa (analogamente per la traiettoria).
Vediamo ora un’altra versione (D. Bohm, 1951). Supponiamo di avere ancora un pione, questa volta il π° (pai zero), quello privo di carica. Esso ha spin zero e lo spin è una quantità che si conserva. Il π° decade in un elettrone (e– ) ed un positone (e+) che schizzeranno via da parti opposte come mostrato in figura 41 (basta cambiare i simboli che denotano le particelle). Per la conservazione dello spin cui accennavo, una misura simultanea degli spin di e– ed e+ deve dare + 1/2 per una particella (ad esempio e+) e – 1/2 per l’altra. Consideriamo ora la situazione sperimentale mostrata in figura 42.
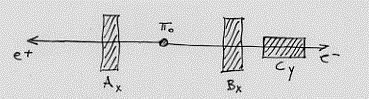
fig. 42
E’ mostrato il pai zero che decade come detto con degli strumenti. Ax e Bx sono due contatori mentre, ad esempio, Cy è un campo magnetico (che ha la proprietà di far ruotare, e quindi cambiare di segno, lo spin). In tal modo lo spin di e– diventa + 1/2. Che succede dello spin di e+ ? Esso dovrebbe essere diventato – 1/2 per rispettare la conservazione dello spin. Ma per saperlo dobbiamo misurare. E quando misuriamo non sappiamo più se lo spin era già cambiato o se lo abbiamo cambiato noi con la misura. Secondo la fisica quantistica operare su e– significa operare sull’intero sistema e non sono valide assunzioni realiste (metafisiche, del tipo quando e+ ha lasciato il contatore Ax prosegue non perturbato in alcun modo, poiché significherebbe ammettere l’esistenza di e+ indipendentemente dall’osservazione. Secondo la Scuola di Copenaghen occorre abbandonare l’atteggiamento realista con tutte le implicazioni filosofiche che ciò comporta. Se poi disponessimo del solo contatore Bx e trovassimo per e– un valore – 1/2 di spin, dovremmo concludere, assumendo una posizione realista, che lo spin di e+ vale + 1/2 già prima dell’operazione di misura. Ma ciò è ancora negato dall’interpretazione della Scuola di Copenaghen.
Vediamo ora il paradosso EPR rappresentato con delle figure (laghetti e pesci):
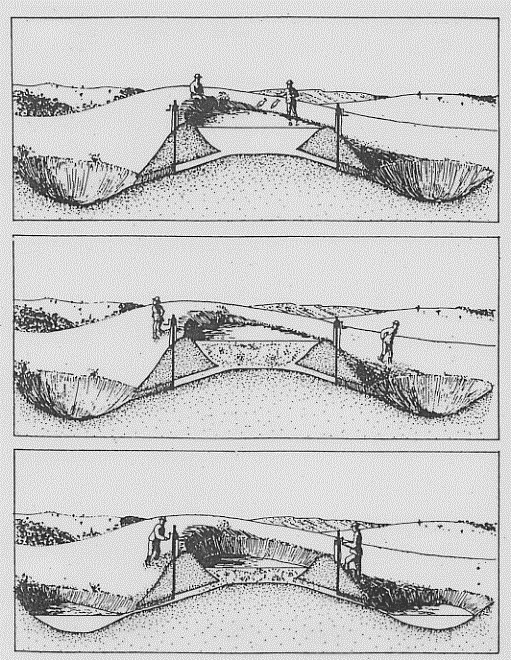
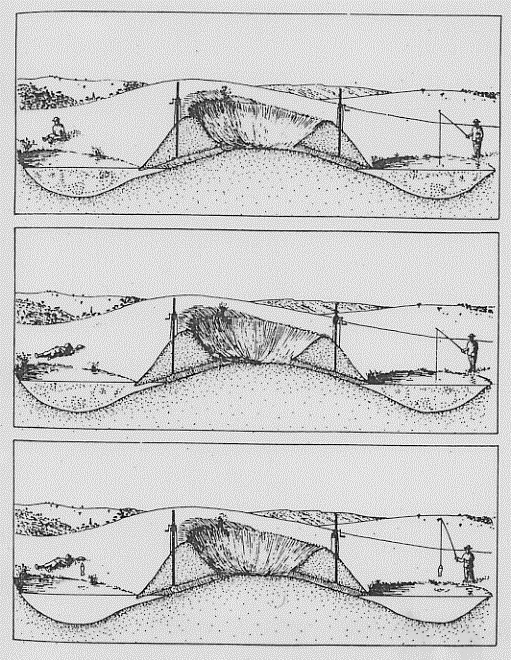
fig. 43
Si gettano due pesci in uno stagno che può essere svuotato in due buche vicine. I pesci, al solito, risultano indeterminati nell’acqua e tale indeterminazione si distribuisce tra i due nuovi stagni. Ma quando un pescatore prende un pesce, anche se l’altro non sta pescando ……gli salta fuori un pesce.
Discutiamo ora un poco l’EPR nella versione di Bohm del 1951 (Bohm ha lavorato su questi problemi dal 1951 al 1980) in cui si sostituiscono le variabili originali (posizione e velocità) con quelle di spin. In questa prima versione si introduce un potenziale quantistico come variabile nascosta. Questo potenziale aveva caratteristiche non-locali (era esattamente definito ed esente da fluttuazioni quantistiche) ed aveva il compito di riunire in sé tutti gli aspetti non classici della teoria dei quanti. Esso non trasporta energia e non si presta ad essere rivelato, però le particelle subiscono i suoi effetti e si servono di esso per comunicare tra loro: la misura effettuata su una particella modifica istantaneamente il potenziale che agisce sull’altra e da ciò deriva la correlazione tra i risultati delle misure. La teoria di Bohm è detta delle variabili nascoste: le misure che noi eseguiamo sembrano seguire leggi probabilistiche solo perché ignoriamo certe proprietà nascoste delle cose che misuriamo.
Questa prima versione della teoria di Bohm fu subito messa in discussione in quanto la relatività impedisce di considerare azioni istantanee a distanza. Il problema era spostato pesantemente altrove. Nel 1980 Bohm fornì una versione delle variabili nascoste che teneva conto delle importanti critiche che erano state rivolte ai suoi lavori del 1951 (soprattutto da parte di Von Neumann). Il livello della realtà nella quale le particelle sembrano essere separate – il livello nel quale viviamo – è chiamato da Bohm ordine esplicito. Il substrato più profondo della realtà, il livello nel quale la separazione tra le particelle scompare e tutte le cose sembrano diventare una parte di un tutto senza discontinuità, è chiamato da Bohm ordine implicito.
Come possono dei segnali andare più veloci della luce?
Se osserviamo su due televisori l’immagine di un pesce in un acquario inviatoci da due telecamere A e B (una disposta di fronte, l’altra di fianco rispetto all’acquario) possiamo supporre che si tratti di due pesci
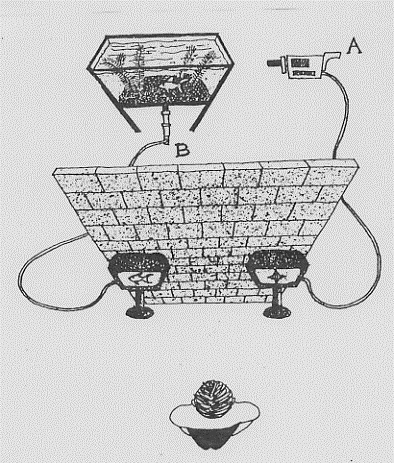
fig. 44
differenti che in alcun modo si comunicano informazioni istantaneamente, anche se le cose non stanno così. Il fatto è che ad un livello più profondo della realtà, quello dell’acquario, i due pesci non sono due entità effettivamente separate. E’ grosso modo ciò che osserviamo quando misuriamo le correlazioni tra le due particelle di EPR. I due televisori rappresentano l’ordine esplicito mentre il pesce nell’acquario rappresenta il livello di realtà dell’ordine implicito. Vi è anche un’ulteriore considerazione: i due schermi TV ci forniscono immagini bidimensionali di una realtà tridimensionale; stesse situazioni, con numero diverso di dimensioni, possono realizzarsi nel mondo subatomico.
Un’altra esemplificazione che fa Bohm è quella dell’ologramma. Un pezzo di una foto
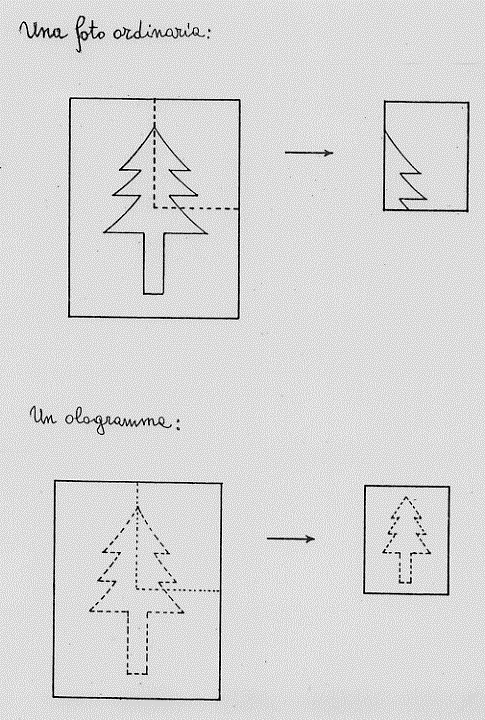
fig. 45
tradizionale, osservata come vogliamo, non ci dice nulla su cosa rappresenta l’intera foto. Un pezzo di un ologramma osservato con luce laser ridà sempre l’immagine dell’intero ologramma (ogni parte dell’ologramma contiene informazioni sull’intero ologramma; allo stesso modo ogni regione dello spaziotempo, per piccola che sia, contiene informazioni sull’ordine implicito dell’intero universo). [Si deve osservare che, ora, la trattazione della teoria di Bohm è fatta tenendo conto delle fluttuazioni quantiche e della quantizzazione dell’azione].
A questo punto mi permetto una piccola libertà: l’irradiato di Renzetti (1998).
fig. 46 – Basta spegnere il geiger per evitare di essere irradiati.
[Sull’EPR si può vedere un articolo di A. Loinger su Il Nuovo Saggiatore, cliccando qui].
BELL E ASPECT (1964 – 1982)
Nel 1964 il fisico irlandese J. Bell riuscì a costruire una disuguaglianza (derivante da semplici regole algebriche) secondo la quale un determinato esperimento con decadimento di particelle e 4 rivelatori avrebbe dovuto fornire un risultato X compreso tra – 2 e + 2 (nella visione realista EPR). Bell sapeva che la fisica quantistica (Scuola di Copenaghen) diceva che questo risultato doveva essere compreso tra (circa) – 3 e + 3:
– visione realista => – 2 ≤ X ≤ + 2
– visione di Copenaghen => – 3 ≤ X ≤ + 3.
Ma Bell non riuscì a realizzare l’apparato sperimentale. Un esperimento in tal senso fu proposto nel 1975 e realizzato nel 1982 da Alain Aspect dell’Università di Parigi Sud. I risultati di tale esperimento hanno mostrato che la natura non obbedisce al teorema di Bell (dettagli divulgativi sull’esperienza di Aspect si possono trovare su: S. Ortoli, J. P. Pharabod – Le cantique des quantiques – La Découverte, Parigi 1984.). E ciò vuol dire non tanto che la meccanica quantistica è corretta quanto che la vecchia visione del mondo non funziona. A questo punto si possono avere almeno 4 possibilità:
La regolazione dei 4 strumenti di misura di Aspect non sono indipendenti a causa di una intrinseca impossibilità. Conseguentemente, se le cose stanno così, ogni esperimento non può che dare un risultato già prevedibile dal momento del big-bang. Conseguentemente ogni affermazione relativa al libero arbitrio è priva di significato.
I rivelatori comunicano istantaneamente tra di loro i risultati delle loro misure. Ma se le cose stanno così allora risultano possibili azioni istantanee a distanza con violazione della relatività (ma abbiamo già osservato che le fluttuazioni e l’effetto tunnel sembrano prevedere fatti del genere).
E’ illegittimo speculare sulla natura della realtà fisica sottostante a questo esperimento. Finché possediamo una teoria che ci fornisce soluzioni che funzionano di cosa ci preoccupiamo ?
Vi sono delle onde che si propagano indietro nel tempo (interpretazione transazionale). All’istante del decadimento la funzione d’onda iniziale si suddivide in due funzioni d’onda una delle quali va avanti e l’altra indietro nel tempo. Le due particelle potrebbero allora comunicare tra loro (si veda punto 2).
Come si vede si risolve una cosa ed il mistero si sposta altrove. Si può quindi dire che, nonostante la confutazione da parte di Bell e Aspect di alcune delle questioni sollevate dall’EPR, i risultati empirici non hanno nulla da dire sul problema; non ci dicono se la completa e corretta teoria sottostante sia probabilistica (Bohr) o deterministica (Bohm). Entrambe le versioni funzionano e, dopo tutti questi sforzi ed analisi, ancora non abbiamo alcuna ragione quantitativa, empirica, per preferire l’una o l’altra. C’è comunque da osservare che Bell, nel ricavare la sua disuguaglianza, ha separato le due questioni che per Einstein dovevano essere inestricabilmente legate: la probabilità e una qualche interconnessione fisica tra le due particelle separate a grande distanza. Aspect ha invece mostrato che questa qualche interconnessione istantanea fa parte della natura, indipendentemente dall’accettazione o meno della fisica quantistica.
Rimane il problema del rivelatore. Se lo descriviamo usando un linguaggio quantistico – si dovrebbe poter fare se effettivamente la fisica quantistica è fondamentale ed universale – allora gli stati indefiniti generano misurazioni indefinite. Nascono allora due possibilità:
o la fisica quantistica è incompleta e si deve aggiungere ad essa una qualche altra teoria che spieghi come si fanno le misure (Selleri propone di elaborare e sviluppare le teorie di Bohm e delle variabili nascoste).
o la fisica quantistica contiene dentro di sé una qualche ricetta, fino ad ora non chiarita, in grado di trasformare in qualche modo uno stato indefinito in uno stato definito (nessuno lavora su tale aspetto).
Il problema della fisica quantistica e la ragione per cui vi sono interpretazioni è che , nonostante decenni di successi pratici della teoria, i fisici non possono ancora sinceramente dire di sapere quale sia il suo significato; essi non riescono, per così dire, a vedere i meccanismi interni della teoria.
Dice Richard Feynman: ” Non possiamo spiegare il mistero nel senso di spiegare come funzioni. Ti diremo solo come funziona. Dicendoti come funziona ti avremo parlato delle peculiarità basilari della meccanica quantistica”.
Ed un tal Samuel Johnson: “Signore, ho trovato per lei una spiegazione, ma non sono obbligato a trovare per lei una comprensione”.
[Sui paradossi della Scuola di Copenhagen si può vedere l’articolo di A. Orefice e R. Giovanelli, Attualità dei paradossi di Copenhagen su Il Nuovo Saggiatore cliccando qui].
ANCORA SULLA MISURA
Iniziamo con il dire che è fuorviante affermare che la misura modifica la cosa misurata perché questa affermazione sembra implicare che un oggetto quantistico si trovi in un qualche stato definito ma ignoto, stato successivamente disturbato da un atto di misura. La misura conferisce determinazione a quantità precedentemente indefinite. L’allievo di Bohr, J. Wheeler sostiene: Nessun fenomeno elementare è un vero fenomeno finché non è misurato.
Il mondo si trova così suddiviso in due classi di oggetti fisici: cose che misuriamo e cose con cui misuriamo. Le cose che misuriamo sono incerte, indefinite, sfocate fino a quando non vengono misurate. Le cose con cui misuriamo esistono sempre in stati definiti: un rivelatore di particelle o le rivela o non le rivela, senza ambiguità. E qui nasce l’incoerenza fatale all’interpretazione di Copenaghen della fisica quantistica. Un dispositivo classico dovrebbe darci risultati privi di ambiguità su un esperimento quantistico. La misura di un fenomeno quantistico non è mai stata definita (e tantomeno spiegata) mediante strumenti quantistici. La misurazione non viene giustificata ma solo affermata. Bohr sapeva ciò e all’obiezione rispondeva con una non risposta: i fisici sanno come misurare le cose. Infatti i fisici hanno sempre misurato come prima dell’introduzione della fisica dei quanti (insomma i fisici capiscono la misurazione come gli avvocati la pornografia e le persone incolte l’arte: non sanno definirla ma sanno cos’è). E Bohr si affidò a questa vecchia capacità dei fisici.
Per quel che riguarda l’infelice gattino di Schrödinger c’è da dire che l’interpretazione rigorosa della Scuola di Copenaghen (principio di complementarità) prevede che è inutile aprire la scatola per vedere come stanno le cose perché il gatto è per metà vivo e per metà morto, stato che non potremo mai osservare. Se poi insistessimo e vgliamo proprio osservare il problema diventa psicologico: quando ? come ? perché ?
Affrontiamo il gatto nei due modi possibili:
1. Gli strumenti funzionano e sono attendibili. Il meccanismo che al 50% genera lo sparo è comandato da particelle che o colpiscono da una parte o colpiscono dall’altra. Per esse non è prevista una situazione indefinita. La vita o la morte del gatto è solo questione di tempo: si apre la scatola e si va a vedere. E’ tutto facile come lanciare una moneta per vedere se viene testa o croce ma la moneta va a finire sotto l’armadio: si tratta di spostare l’armadio per vedere. Solo che non spieghiamo l’efficacia del dispositivo di misura. Se abbiamo comunque fiducia in misure siffatte possiamo pure lasciare in pace il gatto. Ma ciò equivale a dire che la fisica quantistica è una teoria eccellente, dettagliata e completa, ma che occorre una bacchetta magica per darle un senso.
·
2. Le misurazioni diventano reali solo quando uno ne prende nota. Qui ci addentriamo nel paludismo filosofico. Wigner ha proposto questa variante all’esperimento del gatto: dopo un certo tempo la scatola viene aperta da un amico che non comunica cosa ha visto allo stesso Wigner. Lo stato è determinato per l’amico e non lo è per Wigner ? Un evento per alcuni è determinato e per altri no ? Più amici, più osservazioni, più determinazioni, mondi diversi ? A questo punto il rompicapo si ribalta: se l’esistenza di fatti dipende, per me, dalla mia coscienza e, per te, dalla tua, come mai concordiamo su tante cose ? Come mai la fondamentale indeterminazione quantistica del mondo svanisce, a quanto pare, quando ci occupiamo di oggetti quotidiani ? Insomma sembra che la scomparsa dell’indeterminatezza quantistica abbia poco a che fare con la mia osservazione del mondo, o con la tua, o con quella di chiunque altro. Anche qui il problema risulta spostato altrove.
FISICA QUANTISTICA E METAFISICA
La fisica quantistica impone un cambiamento delle nostre idee sulla realtà oggettiva. Un cambiamento fondamentale è l’abbandono di un’analisi del mondo in termini di parti relativamente autonome che esistono separatamente seppure interagenti. L’enfasi principale è ora posta sull’integrità indivisibile con cui gli strumenti di osservazione non si possono separare da ciò che si osserva. La divisione comune del mondo tra soggetto ed oggetto, mondo interno e mondo esterno, corpo e anima non è più adeguata (Heisenberg). Come si può risolvere il paradosso circolare implicito nel fatto che il mondo macroscopico determini la realtà microscopica dalla quale a sua volta è formato ? Ci scontriamo con questo paradosso ogni volta che eseguiamo misure quantistiche. Si deve inoltre tener conto del fatto che se abbiamo due particelle lontane caratterizzate ciascuna dalla propria funzione d’onda, dal momento che esse cominciano ad interagire, anche se si allontanano di nuovo successivamente, dovranno sempre essere trattate con un’unica funzione d’onda.
Everett (1957) ha proposto una interpretazione quantistica basata su universi molteplici. Ogni mondo possibile diventa reale e tutti i mondi alternativi esistono in parallelo. Questa molteplicità di mondi si estende alle scelte dell’uomo.Supponiamo di dover scegliere vino o birra. Secondo Everett, l’universo si divide immediatamente in due rami. In uno dei rami prendiamo il vino e nell’altro la birra. In questo modo

fig. 47 – Disegno che molto lontanamente vuole rappresentare gli universi molteplici.
tutti felici! Il libero arbitrio ne risente un poco: noi volevamo o vino o birra, non vino e birra. Ma il noi qui deve essere suddiviso in due io, ciascuno dei quali sta in un un universo differente e prova desideri e sensazioni diverse. Così, in nome di una esigenza di misura si introduce la metafisica ai livelli più spinti. Il fisico americano Fritjof Capra nel suo Il Tao della fisica individua nell’indistinguibilità tra osservatore (mondo interno) ed osservato (mondo esterno) ciò che da secoli è la filosofia tibetana: nessuna separazione tra i due mondi. E cosa c’è di meglio del dualismo onda-corpuscolo per rappresentarci il dualismo anima-corpo? Poi arrivano i superscemi come il cattolico francescano Talbot che dimostra matematicamente l’esistenza di Dio attraverso i quanti (Beyond the quantum – 1986) e già c’è chi giustifica il paranormale (addirittura i cerchi nel grano sono originati dalle vibrazioni quantistiche – sic! -) e tenta una prova biochimica dell’esistenza dell’anima (in Italia abbiamo avuto Enrico Medi che ha dimostrato la verginità della Madonna con la termodinamica e Zichichi che ha mostrato tante altre cose).
Ma vediamo alcune estrapolazioni che, negli anni, vennero fatte, da varie personalità scientifiche e non a proposito dei quanti.
ESEMPLIFICAZIONI IDEALISTE
La meccanica quantistica sancisce il definitivo fallimento della causalità (Heisenberg 1927)
Se mi si chiede: cos’è la materia ? Rispondo: un insieme di equazioni differenziali (Heisenberg 1933)
Le nuove concezioni che sono sorte dalle esperienze fisiche quantistiche e dalla loro elaborazione teoretica, significano la liquidazione dell’immagine materialistica del mondo … L’atomo …, sprovvisto di tutte le qualità sensibili, è soltanto caratterizzabile con uno schema di formule matematiche, … è solo un concetto accessorio (Jordan 1936)
La dogmatica concezione materialista del mondo non può andare d’accordo con il positivismo dovuto al fatto che la prima è la rappresentazione di una forma particolare di insegnamento metafisico ed ascientifico … La concezione positivista ci offre nuove possibilità per far posto alla religione, senza entrare in contraddizione con il pensiero scientifico (Jordan 1944)
E’ l’interazione finita tra l’oggetto e gli strumenti di misura conseguenza immediata del quanto d’azione e ciò impone la necessità di rinunciare definitivamente all’ideale classico di causalità e di rivedere a fondo il nostro atteggiamento di fronte al problema della realtà fisica (Bohr 1949)
La fisica atomica ha voltato le spalle alla tendenza materialista che ha avuto la scienza nel secolo XIX (Heisenberg 1959)
L’affermazione della concezione determinista della natura secondo la quale Dio è rimasto senza lavoro … ha perso ora il suo fondamento … e, nell’innumerevole quantità di risultati sempre nuovi ed indeterminati si può vedere l’azione, la volontà, la potenza di Dio (Jordan 1963)
Per tutto ciò che sappiamo di fisica e biologia sull’indeterminazione, è certo che scientificamente ora non si può più rifiutare la possibilità logica di affermare il libero arbitrio (Jordan 1963)
Dobbiamo rivedere le nostre idee sulla causalità. La relazione causale si applica solo a sistemi che non siano stati alterati … Hanno significato reale solo le domande relative ai risultati degli esperimenti … (Dirac 1964)
Il concetto di oggetto materiale, di costituzione e natura indipendenti dall’osservatore, è estraneo alla fisica moderna la quale, obbligata dai fatti, ha dovuto rinunciare a questa astrazione (Pauli 1964)
Altre operazioni fatte da Jordan e di seguito riassunte:
- la mancanza di causalità è alla base del libero arbitrio
- la mancanza di causalità è alla base del vitalismo
- la mancanza di causalità è alla base della percezione extrasensoriale
- la fisica quantistica è un sostegno alle teorie di Freud (analoga operazione fece Pauli con Jung)
I teologi si affrettarono ad accettare il principio di indeterminazione come prova dell’indeterminismo e videro in quest’ultimo la base della libertà personale e della responsabilità morale. Il teologo Bavink fece notare l’accordo tra le idee e la politica di Hitler da un lato e le conseguenze antimaterialistiche, cioè idealistiche, vitalistiche ed anticomunistiche della nuova fisica dall’altro lato (citato da Jordan – 1936 – e da Heilbron – 1987 -). Osservo a margine che Heisenberg e Jordan furono due tra i pochissimi fisici della grande scuola tedesca che aderirono al Nazismo.
ESEMPLIFICAZIONI REALISTE
Una teoria fisica non può dipendere dall’abilità degli sperimentatori. Ciò introduce un elemento antropomorfo e quindi innaturale e porta ad un’inaccettabile limitazione della libertà di pensiero ed una mutilazione del principale strumento con cui deve lavorare il teorico (Planck 1927) [in relazione a quanto sosterrà Popper nella prima edizione della Logica della Scoperta Scientifica si ricordi che Planck, sei anni prima – 1929 – , considerò la realtà divisa in tre mondi: quello dei sensi, quello reale e quello fisico].
Questi indeterministi, con il loro antico peccato positivista, confondono ancora il mondo sensoriale con l’immagine del mondo e si sentono autorizzati a concluderne che l’esame dei fenomeni porta necessariamente all’abbandono del principio di causalità (Planck 1933) …
… potranno discenderne, e non solo nell’ambito della fisica, conseguenze davvero pericolose (Planck 1929)
La convinzione che esista un mondo esterno, indipendentemente dal soggetto che lo percepisce, è la base di tutta la scienza naturale. Poiché, però, la percezione sensoriale ci fornisce solo una informazione indiretta su questo mondo esterno, o “realtà fisica”, noi possiamo affermare quest’ultima solo con mezzi speculativi. Ne deriva che le nostre nozioni di realtà fisica non possono mai essere definitive (Einstein 1934)
Ogni elemento della realtà fisica deve avere una controparte nella teoria fisica (Einstein 1935)
Ogni esame serio di una teoria fisica deve tener conto della distinzione tra la realtà oggettiva, che è indipendente da qualsiasi teoria, ed i concetti fisici con i quali la teoria opera. Questi concetti sono intesi corrispondere alla realtà oggettiva e mediante questi concetti ci formiamo un’immagine di questa realtà (Einstein 1935)
Sembra difficile guardare le carte di Dio, ma neanche per un attimo posso credere che Egli giochi a dadi e faccia uso di mezzi “telepatici” (come la teoria quantistica corrente pretende che faccia (Einstein 1942)
[noto a margine che Einstein lavorò almeno fino al 1920 alla ricerca di una Teoria unificata dei campi dalla quale la Fisica dei quanti potesse essere dedotta come caso particolare].
L’idea di complementarità ha avuto molto successo e si sono fatti molti tentativi, nella maniera più pericolosa, di estrapolazione fuori della fisica, ad esempio, nella biologia, sociologia, psicologia, ecc. (De Broglie 1964)
Di fronte a fenomeni di interferenza e di diffrazione, un fisico senza una teoria preconcetta si vede obbligato a credere che si tratta della propagazione di onde reali, e non una semplice rappresentazione di una probabilità che solo esiste nella sua mente (De Broglie 1964)
I brani di Dirac che seguono mostrano che il fisico britannico cambiò opinione con il passare degli anni:
Mi sembra evidente che ancora non possediamo le leggi fondamentali della meccanica quantistica. Le leggi che stiamo studiando ora avranno bisogno di qualche modificazione importante prima di poter dire di possedere una teoria relativista. E’ molto probabile che questa modificazione … sia tanto drastica come la modificazione che portò dalla teoria delle orbite di Bohr fino alla meccanica quantistica attuale (Dirac, Roma 1974)
Penso che alla fine potrebbe accadere che fosse Einstein ad avere ragione, perché la forma attuale della meccanica quantistica non dovrebbe essere considerata come la forma definitiva. Ci sono grandi difficoltà … E’, per ora, la migliore teoria che possediamo però non credo che sopravviverà indefinitamente nel futuro. E credo sia molto probabile che da un momento all’altro si riesca a costruire una meccanica quantistica migliore, nella quale ritornerà il determinismo e giustificherà, pertanto, il punto di vista di Einstein (Dirac 1975)
La storia di un Einstein che con l’età diventa conservatore è, dopo lo studio dei suoi scritti, drammaticamente capovolta. Perché è proprio Bohr che viene fuori come il conservatore che non vuole (o non può) assistere al rovesciamento del sistema dei concetti classici e quindi li difende ricorrendo a presunte necessità concettuali …, mentre, per quanto riguarda l’uso di concetti classici, il metodo analitico di Einstein è l’espressione di un grande senso critico, una mosca cocchiera che non veniva facilmente tacitata (A. Fine – The Shaky Game: Einstein, Realism and the Quantum Theory – The University Chicago Press, 1986, pag. 19).
BIBLIOGRAFIA
Riferendosi solo a testi divulgativi sulla fisica dei quanti ve ne sono ormai, a diverse dignità, centinaia. Io ne riporterò solo qualcuno che ritengo meritevole di attenzione:
A. Bandini Buti – I quanti di Planck (le molecole – la radiazione) – Ed. Delfino, Milano 1963
A. Bandini Buti – Meccanica ondulatoria e quantistica – Ed. Delfino, Milano 1962.
J. A. E. Silva, G. Lochak – Onde e corpuscoli – Il Saggiatore, Milano 1966
J.C. Polkinghorne – Il mondo dei quanti – Garzanti, Milano 1986
G. Gamow – Trent’anni che sconvolsero la fisica – Zanichelli, Bologna 1966
V. Ridnik – Qu’est-ce que la mécanique quantique? – Editions MIR, Mosca 1969
R. Gilmore – Alice nel paese dei quanti – Raffaello Cortina, Milano 1996
Riporto ora una bibliografia (certamente non esaustiva) sui problemi che la fisica quantistica pone:
L. I. Ponomarev – The quantum dice – MIR Publishers, Mosca 1988
D. Lindley – La luna di Einstein – Longanesi, Milano 1966
P. Nutricati – Oltre i paradossi della fisica moderna – Dedalo, Bari 1988
S. Petruccioli – Atomi, metafore, paradossi – Theoria, Roma – Napoli 1988
S. Ortoli, J. P. Pharabod – Le cantique des quantiques – La Découverte, París 1984
M. E. Omelyanovskij, V. A. Fock e altri – L’interpretazione materialistica della meccanica quantistica – Feltrinelli, Milano 1972
AA. VV. – Quanti e realtà – Sansoni, Firenze 1967
F. Capra – Il Tao della fisica – Adelphi, Milano 1982
M. Bunge – La causalità – Boringhieri, Torino 1970
M. Talbot – Beyond The Quantum – Bantam Books, Toronto 1986
I testi che seguono li fornisco nell’edizione spagnola che io ho studiato. Non lo faccio nella lingua originale perchè, in Spagna, non hanno la buona abitudine di riportare tutti i dati relativi all’edizione originale:
P.Forman – Cultura en Weimar, causalidad y teoría cuántica, 1918-192 – Alianza Universidad, Madrid 1984
J. M. Jauch – Sobre la realidad de lo cuantos – Alianza Universidad, Madrid 1985
A. Rae – Física cuántica. Ilusión o realidad ? – Alianza Universidad, Madrid 1986
J. S. Bell – Lo decible y lo indecible en mecánica cuántica – Alianza Universidad, Madrid 1990
F. Selleri – El debate de la teoría cuántica (con prefazione di Popper) – Alianza Universidad, Madrid 1986
F. Selleri – Física sin dogma – Alianza Universidad, Madrid 1984
D. Bohm – La totalidad y el orden implicado – Kairós, Barcelona 1988
J. Gribbin – En busca del gato de Schrödinger – Salvat, Barcelona 1986
I testi che seguono sono di coloro che hanno lavorato in prima persona all’elaborazione della fisica dei quanti:
M. Planck – Scienza, filosofia e religione – Fabbri, Milano 1973
M. Planck – La conoscenza del mondo fisico – Einaudi, Torino 1943
M. Planck – Autobiografia scientifica – Einaudi, Torino 1956
N. Bohr – Teoria dell’atomo e conoscenza umana – Boringhieri, Torino 1961
N. Bohr – Sui sentieri della vita – Boringhieri, Torino 1965
W. Heitler – Causalità e teleologia nelle scienze della natura – Boringhieri, Torino 1967
L. de Broglie – Sui sentieri della scienza – Boringhieri, Torino 1962
Heisenberg, Schrödinger, Born, Auger – Discussione sulla fisica moderna – Boringhieri, Torino 1959
W. Heisenberg – Natura e fisica moderna – Garzanti, Milano 1957
W. Heisenberg – Fisica e oltre – Boringhieri, Torino 1984
M. Planck – Initiations a la physique – Champs/Flammarion; París 1941
E. Schrödinger – Scienza e umanesimo. Cos’è la vita ? – Sansoni, Firenze 1970
Per inquadrare le cose di cui si parla è utile tenere presente almeno una storia della fisica dei quanti:
G. Tagliaferri – Storia della fisica quantistica – Franco Angeli, Milano 1985
ed un approfondimento di qualche suo aspetto:
AA. VV. – Contributi alla storia della meccanica quantistica – Domus Galileiana, Pisa 1976
Un’ottima discussione di varie questioni quantistiche si trova in:
AA.VV. – La fisica dei quanti – Le Scienze quaderni n° 33, Milano 1982
Categorie:Attualità, Senza categoria
Rispondi