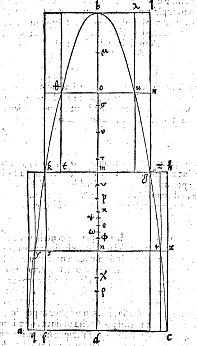
Una delle figure che compaiono nel Liber di Commandin9o e relative al
calcolo del centro di gravità del conoide parabolico.

        Sui centri di gravità dei solidi
tutti i grandi matematici dell’epoca si cimentarono e, oltre a Commandino, lo
fece tra gli altri anche Francesco Maurolico nel suo Archimedis
de momentis aequalibus ex traditione (1518). E, come osserva
correttamente Giusti, l’interesse non sta nel risultato in sé, ma piuttosto
nel fatto che, in mancanza di un linguaggio algebrico che ne permettesse una
formulazione trasparente, gli enunciati erano molto complicati, spesso oscuri,
e talvolta, come nel caso dell’ultimo teorema del trattato di Commandino, di
dubbia generalità. Così quello che conta in questi casi non è trovare il centro
di gravità, ma esprimere il risultato nel modo più semplice e immediato.

        In questo senso è utile vedere
la differenza che esiste tra Commandino e Galileo confrontando il medesimo
teorema nelle formulazioni prima di Commandino e quindi di Galileo:

Commandino. Il centro di gravità di un qualunque frusto tagliato da una
porzione di conoide rettangolo sta sull’asse, in modo che tolti dapprima dal
quadrato del diametro della base maggiore la sua terza parte e due terzi del
quadrato del diametro della base minore; e poi dalla terza parte del quadrato
della base minore tolta una parte a cui il rimanente del quadrato della base
maggiore insieme con la detta porzione abbia proporzione doppia di quella che
ha il quadrato della base maggiore al quadrato della minore: il centro sta in
quel punto dell’asse, che lo divide in modo che la parte che tocca la base
minore all’altra parte abbia la stessa proporzione che al quadrato della base
minore tolto dai due terzi del quadrato della maggiore ha ciò che rimane
insieme con la porzione tolta dalla terza parte del quadrato della maggiore
alla restante porzione della stessa terza parte.
 

Galileo. Il centro di gravità di un qualunque frusto tagliato da un
conoide parabolico sta sull’asse; e diviso questo in tre parti uguali, il
centro di gravità sta in quella di mezzo e la divide in modo che la parte verso
la base minore alla parte verso la base maggiore ha lo stesso rapporto che la
base maggiore alla base minore.

       Sembra evidente quale sia stato il
passo in avanti tra le due formulazioni e lo stesso si potrebbe mostrare per
ogni altro teorema enunciato e dimostrato dai due ma, ripeto, la dimostrazione
era ormai scontata, quello che contava era la chiarezza dell’enunciato.

        Poiché era relativamente
semplice occuparsi dei centri di gravità di tutte le altre figure di cui si era
occupato Commandino, ed in Galileo vi è solo la maggiore chiarezza espositiva,
vediamo come Galileo affronta il teorema relativo al conoide parabolico.
Intanto anche qui si fa uso di figure inscritte e circoscritte che gradualmente
vanno approssimandosi dall’interno e dall’esterno alla figura data. In Galileo
si segue un procedimento differente anche perché alcune cose che Commandino
ricava egli le dà come postulati. Seguiamo ciò che scrive Camerota:

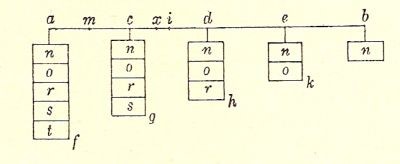
Tornando ai Theoremata
circa centrum gravitatis solidorum [di Galileo], mette conto di
notare come Galileo dimostri preventivamente che, sospendendo dei pesi eguali, raggruppati
secondo una progressione aritmetica, a distanze identiche lungo una bilancia,
il centro di gravità del sistema divide la bilancia secondo un rapporto 2:1.
Cosi (come si può notare dalla figura qui sotto riprodotta), date le grandezze
f, g, h, k e n, il cui peso aumenta progressivamente di un eccesso pari a n, il
centro di gravità cadrà nel punto x, in modo tale  che bx = 2xa.

Categorie:Galileo Galilei