Ingegneria Meccanica – Roma Tre

AA/2011-2012

APPUNTI PER IL CORSO

(Ripresi integralmente e da me assemblati dai testi di bibliografia)

Roberto Renzetti

Bibliografia: R. Renzetti –Vari appunti miei raccolti negli anni -www.fisicamente.blog

LA COMPOSIZIONE RELATIVISTICA DELLE VELOCITA’

         Poiché il principio di costanza di c comporta che c è una velocità limite, la legge di composizione di velocità di Galileo deve essere cambiata.

         Se infatti si dovessero comporre le velocità con la regola di Galileo, risulterebbe che la luce, emessa da un faro posto sull’estremità anteriore di un razzo che si muove con velocità v, avrebbe velocità c + v, superiore cioè a quella emessa come limite superiore per la luce.

         Per trovare le equazioni che ci permettano di comporre le velocità relativisticamente (nel senso di Einstein), possiamo ancora ricorrere alle trasformazioni di Lorentz (8).

        Riferiamoci ancora alla figura 50 e supponiamo di avere un oggetto che si muova con velocità u’_x lungo l’asse x’ di S’. Su S’ varrà la relazione che notoriamente ci fornisce la velocità, e cioè:  u_x = Δx’/Δt’ con Δx’ = x’₂ – x’₁  e Δt’ = t’₂ – t’₁.

        Anche su S varrà una analoga relazione, e cioè: u_x = Δx/Δt con Δx = x₂ – x₁ e Δt = t₂ – t₁, solo che ora da S si osserverà l’oggetto in considerazione muoversi con una velocità somma della sua e di quella del sistema S’. In sostanza da S si osserva una composizione di velocità.

        Sviluppiamo allora l’ultima relazione scritta utilizzando le trasformazioni di Lorentz. Si ha (ricordando che v è la velocità con cui il riferimento S’ è in moto rispetto ad S):

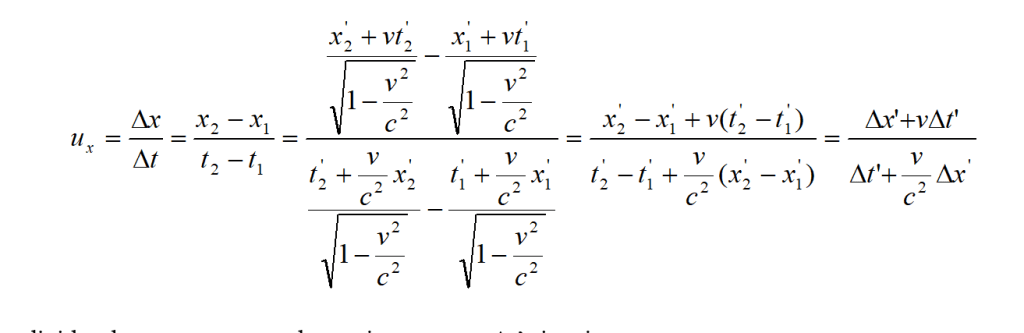
dividendo numeratore e denominatore per Δt’ si ottiene:

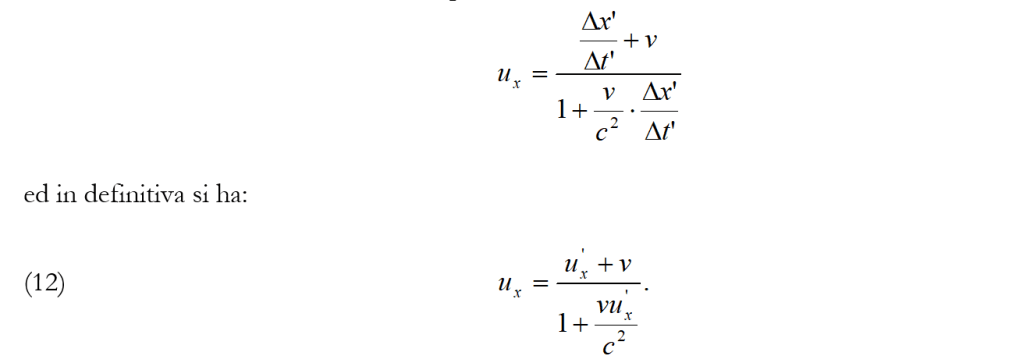
           Nello stesso modo per u’_x si trova:

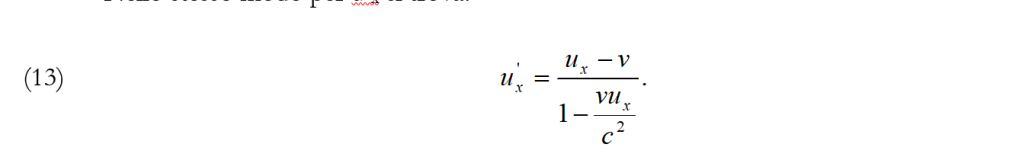
            Alla (13) si può anche arrivare, per il principio di relatività ponendo nella (12) al posto di u_x, u’_x, v, rispettivamente  u’_x, u_x, -v.

             La (12) e (13) forniscono la composizione relativistica delle velocità. Andiamo a vedere se soddisfano le condizioni per le quali le andavamo cercando.

Supponiamo che si abbia  u’_x = c. La (12) diventa allora:

ed anche qui tutto torna.

        Il risultato è più generale di quanto qui mostrato e, qualunque siano i valori di u’_x e v, le equazioni (l2) e (l3) soddisfano il principio di costanza della velocità della luce.

        Ferme restando le condizioni sul parallelismo degli assi per i due riferimenti S ed S’ da noi presi in considerazione (e che ci portano ad affermare y = y’ e z = z’), è possibile che un oggetto in moto in uno dei dati riferimenti abbia una velocità non parallela all’asse x, fatto quest’ultimo da noi presupposto nel ricavare le relazioni (l2) e (l3).

        Supponiamo, per ragioni di semplicità, che la velocità dell’oggetto da noi preso in considerazione abbia, in S’, la direzione ed il verso mostrato in figura 52.

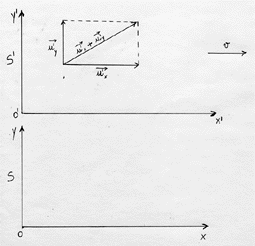
Figura 52

Il nostro oggetto, in S’, ha allora, una velocità data dalla somma vettoriale di u’_x  e di u’_y, data cioè da u’_x + u’_y, con ovvio significato dei simboli.

        II valore u_x di u’_x, misurato nel riferimento S, è quello fornito dalla (12); cerchiamo ora di trovare u_y.

        Sappiamo che y = y’ e quindi che Δy = Δy’. Inoltre Δt e Δt’ hanno lo stesso valore che abbiamo in precedenza trovato. Ed allora, per l’osservatore in S, risulterà:

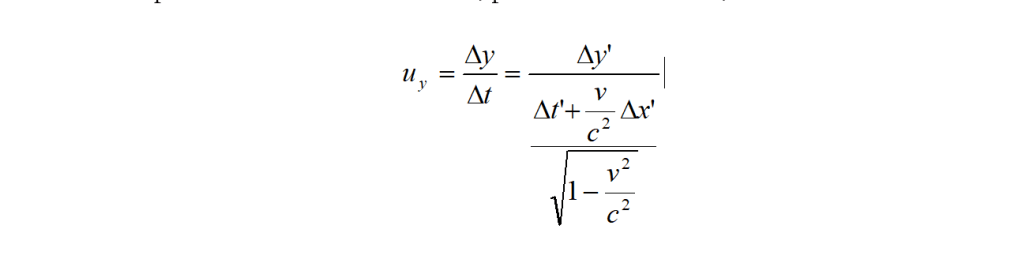
e, dividendo numeratore e denominatore per Δt, si trova:

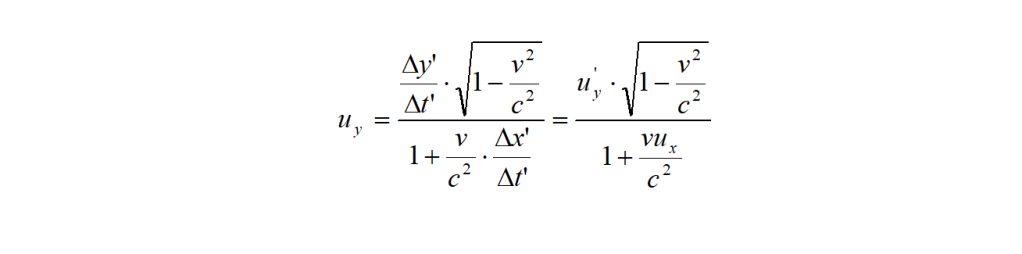
nello stesso modo, per u’_y si trova:

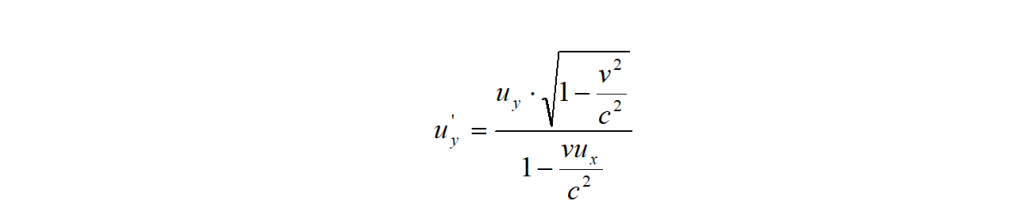
        Facendo un conto uguale a quello ora fatto,  ricordando che z = z’ (e quindi  Δz = Δz’) e che valgono le stesse relazioni per Δt e  Δt’, si può facilmente trovare la componente u’_z  della velocità di un oggetto comunque diretta rispetto agli assi x’, y’, z’.

        Si trova:

Ricapitolando, le formule di composizione delle velocità per S ed S’ rispettivamente, sono:

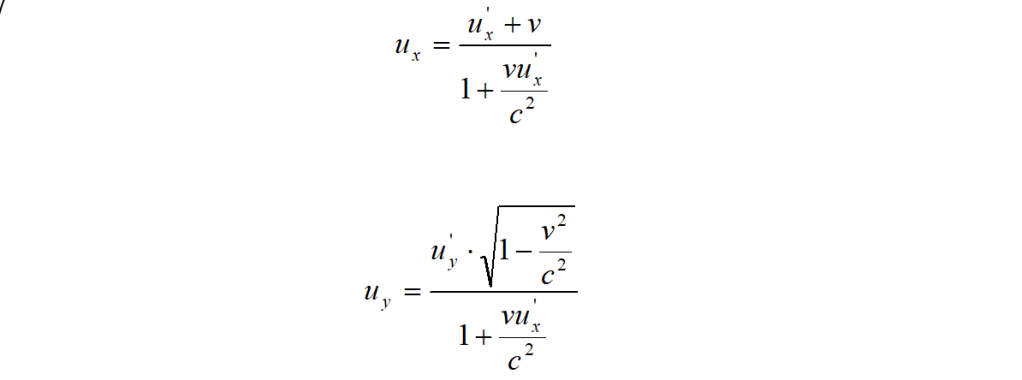
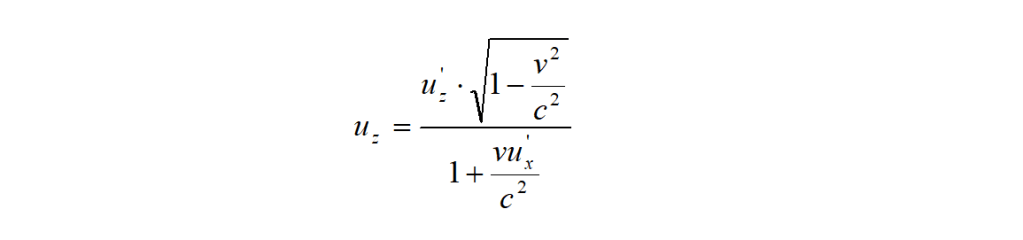
(14)

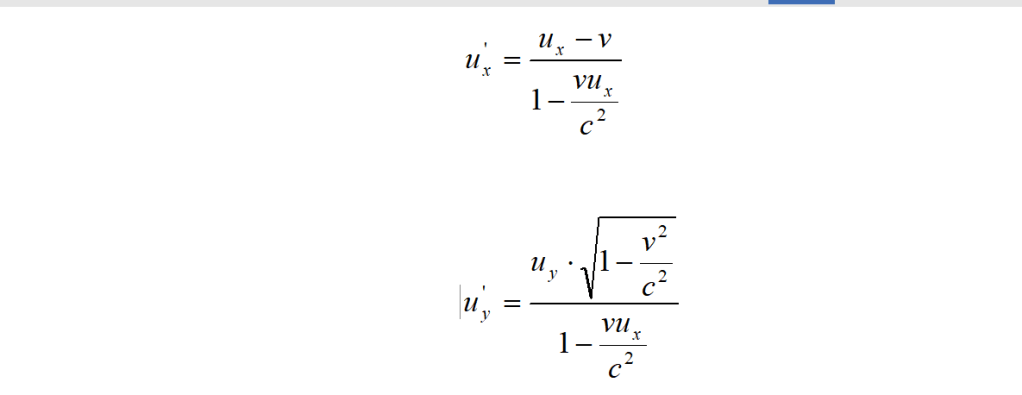
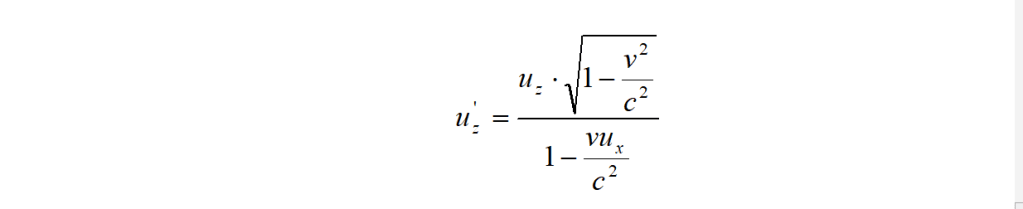
Categorie:Senza categoria