Ingegneria Meccanica – Roma Tre

AA/2011-2012

APPUNTI PER IL CORSO

(Ripresi integralmente e da me assemblati dai testi di bibliografia)

Roberto Renzetti

Bibliografia: R. Renzetti –Vari appunti miei raccolti negli anni -www.fisicamente.blog

RELATIVITA’: ALCUNE VERIFICHE SPERIMENTALI

        La relatività ristretta ha un completo e totale riscontro sperimentale in tutti i campi della fisica non avendo avuto fino ad ora (1983) nessuna confutazione dall’esperienza.                      

        E’ comunque utile fare una breve rassegna delle sue conferme sperimentali, a partire dal postulato di costanza della velocità della luce.  (925)

LA COSTANZA DELLA VELOCITA’ DELLA LUCE

        La prima evidenza sperimentale della costanza di c fu fornita (1913) dall’astronomo De Sitter mediante l’osservazione delle stelle doppie (figura 70). La luce proveniente sulla Terra da un sistema

Figura 70

binario di stelle, in rotazione intorno al loro baricentro O, dovrebbe comporsi con la velocità v delle stelle. Dalla posizione 1 la luce dovrebbe arrivare sulla Terra, secondo la composizione di Galileo, con velocità c – v, mentre nella posizione 2 con velocità c + v. Se ciò fosse vero, data la differenza dei tempi d’arrivo della luce da 1 e 2, l’orbita delle due stelle (che nella nostra esemplificazione à supposta circolare) dovrebbe apparire eccentrica. I dati sperimentali non mostrano l’eccentricità in oggetto. Una conclusione possibile è che c sia indipendente dalla velocità della sorgente, in accordo con il secondo postulato di Einstein.

Alcune critiche di Fox (1962) alle conclusioni che abbiamo ora proposto, dettero il via a tutta una nuova serie di esperimenti. Tra questi quello di Alväger (1964) fu riconosciuto, anche dallo stesso Fox, come probante delle conclusioni in oggetto.

Altre conferme della costanza di c vennero dai lavori di Quirino Majorana (1919) che utilizzò sorgenti luminose terrestri e specchi in rapido movimento. E quindi altri innumerevoli lavori tra i quali sono da segnalare quelli di Kennedy e Thorndike (l932) e Farley (1964). Altra notevole esperienza per mostrare che c è una velocità limite è quella di W. Bertozzi (l963).

L’ESPERIENZA DI MICHELSON – MORLEY

        Poiché tutti i sistemi inerziali sono equivalenti, non è possibile evidenziare il moto assoluto di uno di essi. Assunta la Terra come sistema inerziale (per il breve tempo necessario a eseguire una misura di una esperienza), se su di essa conduciamo una qualsiasi esperienza, anche supponendo che la Terra sia dotata di un qualunque moto traslatorio (sconosciuto) a velocità costante, il risultato di questa esperienza sarà lo stesso che si misurerà su tutti gli altri sistemi inerziali dotati di moto traslatorio uniforme rispetto alla Terra (principio di relatività).

        Ma assumiamo pure che vi sia un etere stazionario. Condotta l’esperienza di Michelson nel riferimento dell’etere immobile, essa dovrà dare evidentemente risultato nullo (poiché la velocità della luce è la stessa in tutte le direzioni di un dato sistema inerziale). In definitiva, nell’ipotesi di bracci uguali e lunghi l , il tempo t  necessario affinché la luce percorra un braccio andata e ritorno sarà uguale al tempo t  necessario alla luce a percorrere andata e ritorno l’altro braccio. Necessariamente, quindi, la differenza Δt dei tempi sarà uguale a zero.

        Ed anche se l’apparecchio viene ruotato di 90°, data la costanza di c in tutte le direzioni, il risultato resterà lo stesso. Se poi l’interferometro ha bracci di lunghezza diversa e, per una data posizione di esso, compaiono frange di interferenza, queste ultime non risulteranno spostate per una rotazione di 90° (e qualunque) dell’intero apparato.

        Ebbene, dati questi risultati nel sistema supposto in quiete, il principio di relatività ci garantisce che esattamente gli stessi risultati si avranno in tutti gli altri sistemi inerziali. 

L’EFFETTO DOPPLER

          Supponiamo che un’onda luminosa trasversale si propaghi nel vuoto lungo l’asse x’ di un dato riferimento S’ (figura 73). Sia A’ l’ampiezza dell’onda, ν’ la sua frequenza, c la sua velocità ed abbia

Figura 73

equazione:

Se osserviamo la propagazione della stessa onda da un altro riferimento S, rispetto al quale S’ si allontana eoa moto traslatorio uniforme a velocità v, per il principio di relatività (e le trasformazioni di Lorentz) dovrà risultare:

y  = y’

e cioè:

e poiché A = A’ (per le trasformazioni di Lorentz y  = y’) la precedente uguaglianza si riduce alla:

Applichiamo ora le trasformazioni di Lorentz a t’ ed x’ che compaiono nel secondo membro. Si trova:

e, sviluppando:

Abbiamo cosi trovato la formula relativistica per l’effetto Doppler. Si noti che, da quanto premesso, ν’ rappresenta la frequenza della sorgente mentre ν la frequenza osservata. Se si confronta la (46) con l’espressione classica, ci si rende conto che quest’ultima è approssimata a termini del primo ordine in v/c e che inoltre, sempre da quest’ultima, sarebbe possibile risalire a riconoscere il moto assoluto o della sorgente o dell’osservatore. Queste difficoltà non si pongono per la (46).

        La formula (46) da noi ricavata è comunque valida nel caso in cui vi sia un moto parallelo di allontanamento con velocità v tra sorgente ed osservatore, non interessando in alcun modo quale dei due o se tutti e due si stanno allontanando. Nel caso più generale, in cui le direzioni del moto della luce e dell’osservatore formino tra loro un certo angolo α , purché si tratti sempre di allontanamento reciproco, la formula relativistica per l’effetto Doppler diventa:

Questa formula fornisce subito la (46) quando α = 0 (quando cioè le direzioni del moto della luce e dell’osservatore, che si stanno allontanando, sono parallele). Nel caso in cui α = 180° (quando cioè le direzioni del moto della luce sono parallele ma hanno verso opposto, il che vuol dire che sorgente ed osservatore si vanno avvicinando) si ha:

Ma, d’altra parte, dato il principio di relatività, questo risultato lo si poteva ricavare direttamente dalla (46) sostituendo ν e -v, rispettivamente, a  ν’  e v.

Nel caso di avvicinamento tra sorgente ed osservatore, nel caso più generale in cui questo avvicinamento avvenga secondo un dato angolo α tra le direzioni del moto, vale la relazione:

Ma discutiamo ancora la (47) e, a questo punto, la (49) che rappresenta lo stesso fenomeno. Se α = 90°, se cioè le direzioni del moto tra sorgente ed osservatore sono perpendicolari, cosa succede ? Poiché cos 90° = 0, sia la (47) che la (49) ci dicono che:

Questo è un fatto di grande importanza. E’ la previsione sperimentale di un effetto Doppler trasversale che in nessun caso rientrava nelle formulazioni classiche. Se cioè osserviamo la propagazione di onde elettromagnetiche perpendicolarmente alla direzione del loro moto, misuriamo una frequenza ν più piccola della frequenza ν’ della sorgente. Questo fatto fu previsto da Einstein nel 1907 e fu confermato sperimentalmente da Ives e Stilwell (1938 e 1941) e questa conferma sperimentale, tra l’altro, risultò la prima prova a sostegno della dilatazione del tempo in un riferimento in moto rispetto ad un altro (noi) considerato in quiete. Che cosa vuol dire infatti misurare una frequenza più piccola di quella della sorgente, se non che i fenomeni in quel riferimento risultano rallentati ?

I MUONI

II fenomeno di dilatazione del tempo fu messo in evidenza anche da una importante esperienza che Rossi ed Hall realizzarono nel 1941.

        Nelle alte zone dell’atmosfera i raggi cosmici ad alta energia, principalmente protoni, interagiscono con i nuclei degli atomi di gas ivi presenti. Queste interazioni generano dei mesoni veloci (i pioni) che in tempi brevissimi decadono in un altro tipo di mesoni (i muoni ). Queste ultime particelle, dotate di carica, hanno una massa che è circa 200 volte quella dell’elettrone ed hanno una velocità vicina a quella della luce (v ≈ 0,998 c). Dopo un tempo brevissimo i muoni si disintegrano producendo un elettrone,

un neutrino ed un antineutrino. La vita media di questi muoni, misurata quando essi sono (quasi) a riposo è  Δt’ = 2.10^-6  secondi. Anche viaggiando alla velocità della luce, con questa vita media, un muone prodotto negli alti strati dell’atmosfera potrebbe percorrere un tragitto pari a:

l’ =  Δt’.c  = 2.10^-6.3.10⁸ = 600 m

solo 600 metri.

        Ebbene, questi muoni non potrebbero mai raggiungere il livello del mare (almeno classicamente). Eppure una gran quantità di essi raggiunge il livello del mare (questo è il motivo per cui sovente si parla di paradosso dei muoni).

        La teoria della relatività rende facilmente conto del fenomeno là dove si utilizzi l’equazione (10bis) sulla dilatazione dei tempi.

         Consideriamo al solito due riferimenti: quello S’ solidale con il muone e quello S solidale con noi osservatori che ci troviamo sulla Terra. Su S’ la vita media del muone sarà  Δt’ = 2.10^-6  sec. Nel nostro riferimento S la vita del muone sarà data dalla (10 bis):

dove v è la velocità del muone rispetto alla Terra (riferimento S). Poiché  v è molto grande (v ≈ 0,998 c) la quantità al denominatore sarà molto piccola e, di conseguenza, Δt risulterà molto più grande di Δt’. Si ha:

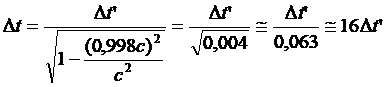
e ciò vuol dire che Δt è 16 volte più grande di Δt’.

Il muone vedrà allora la nostra atmosfera contratta secondo la (11):

ed il loro breve tempo di vita,  data la contrazione delle lunghezze che loro osservano,  permette loro di giungere al livello del mare. Sviluppando infatti la (11) e sostituendo a (1 – v²/c²)^1/2 il valore trovato nello sviluppo precedente (1/16) si ha:

e cioè il valore l relativo al percorso del muone che noi osserviamo diventa di 9.600 m, sufficiente a far si che noi possiamo osservare una gran quantità di muoni al livello del mare.

        Il ragionamento può anche rovesciarsi. Osservato sperimentalmente che molti muoni arrivano alla superficie del mare, moltiplicando per circa 16 volte il tragitto che dovrebbero percorrere rispetto ad un riferimento solidale con essi, vuol dire che questi muoni viaggiano mediamente ad una velocità pari a 0,998 c.

        Esperimenti sulla dilatazione del tempo non più con orologi naturali come i muoni, ma con orologi atomici in volo ad alta quota, sono stati effettuati nel 1971 da Hafele e Keating e nel 1975-1976 da un gruppo di ricercatori dell’Università del Maryland. Ambedue gli esperimenti hanno confermato il fenomeno di dilatazione.

        Ora o questi fenomeni di dilatazione del tempo sono perfettamente reciproci se osservati dall’altro riferimento, oppure bisogna negare il principio di relatività (il riferimento nel quale il tempo non si dilata è il riferimento assoluto).

        Dico questo perché alcuni fisici, anche importanti, tendono ad assegnare un valore assoluto a tale dilatazione. Occorre, una volta per tutte, ricordare che in tutti questi esperimenti c’è sempre un confronto a riposo degli orologi e quindi la messa in moto di uno di essi. In definitiva si ha sempre a che fare col moto accelerato di uno dei due riferimenti (nel caso dei muoni si ha la decelerazione di essi al momento dell’impatto con il rivelatore e la loro accelerazione nel momento in cui sono creati). Come lo stesso Einstein ha più volte osservato, nessuno ci garantisce che strani fenomeni abbiano luogo proprio nei momenti in cui si ha a che fare con le accelerazioni.

IL PARADOSSO DEI GEMELLI

        E’ un paradosso (?) che fu ideato dal fisico francese P. Langevin (l911) sull’onda del paradosso degli orologi ideato dallo stesso Einstein nel suo lavoro del 1905.

        Il paradosso consiste in questo.

        Uno di due gemelli parte dalla Terra per un viaggio spaziale ad una velocita dell’ordine di grandezza di quella della luce. Dopo qualche tempo, tornato sulla Terra, trova il suo gemello più vecchio di lui. Certo, qualcuno potrebbe dire, egli è stato in viaggio ad una fantastica velocità, per

lui il tempo si è dilatato (è passato più lentamente) e quindi è rimasto più giovane del suo gemello restato sulla Terra. Ed allora, dov’è il paradosso?

        Secondo il principio di relatività i due sistemi di riferimento (Terra e razzo) devono poter essere considerati equivalenti ed il razzo che si allontana rispetto alla Terra deve poter essere descritto come Terra che si allontana dal razzo (per altri versi quest’ultima conclusione non è corretta in quanto il razzo, per allontanarsi dalla Terra, deve accelerare). Ed allora, in questa seconda descrizione, è il gemello che si trova sulla Terra che deve mantenersi più giovane. Ciò vuol dire che, in ultima anali-

si, al loro reincontro i due gemelli dovrebbero avere la stessa età.

        Per questo si parla di paradosso, perché, secondo svariati e qualificati autori, è proprio il gemello che viaggia in astronave ad invecchiare. Non sono in grado di intervenire autorevolmente in una disputa che dura da più di 80 anni. Posso solo dire che i due sistemi (terra e razzo) sono confrontati a riposo (i due gemelli devono almeno essere nati dalla stessa madre !); i due sistemi dovranno ancora essere confrontati a riposo (al momento del ritorno dell’astronave sulla Terra); si ricordi che quando abbiamo parlato di simultaneità abbiamo escluso la possibilità di sincronizzare due orologi a riposo e quindi di metterne in moto uno (nessuno garantiva che il moto non alterasse il ritmo di quell’orologio); quando un gemello si pone in viaggio accelera per raggiungere la sua folle velocità; lo stesso Einstein

non ha fatto mai confronti di orologi a riposo trasferendoli poi su differenti sistemi inerziali animati di moto rettilineo uniforme l’uno rispetto all’altro; quel gemello in viaggio deve poi decelerare per poggiarsi sulla Terra; egli deve poi essere dotato di un moto accelerato (almeno accelerazione centripeta) durante il viaggio, se vuole girare e tornare sulla Terra. La relatività ristretta parla esclusivamente di sistemi inerziali in moto uniforme e rettilineo gli uni rispetto agli altri; il principio di relatività dice che i fenomeni relativistici devono godere di perfetta reciprocità (se da un riferimento si misura una dilatazione del tempo su un altro riferimento, da quest’ultimo si deve misurare la stessa dilatazione sul primo); la relatività non può pronunciarsi sulla realtà degli effetti di dilatazione o contrazione o, meglio, sulla loro assolutezza (in quest’ultimo caso lo stesso principio di relatività deve essere buttato via); la relatività riguarda solo effetti di misura da un riferimento ad un altro è impossibile ogni confronto a riposo.

        Sulla strada comunque di ammettere la non assolutezza degli effetti relativistici: oltre a W. Pauli, .J. Perrin, R. Dugas, A. M. Tonnellat, i nostri Palatini e Straneo. Sembra poi che vi sia un coro di studiosi che affermano la realtà dell’effetto gemelli.

        Dal mio punto di vista posso fare solo qualche timida obiezione alla realtà di questo effetto. La Terra torna ad essere un riferimento assoluto rispetto al quale si possono dare dei tempi assoluti ? Che ne è della reciprocità tra i diversi sistemi inerziali ? Supposto, ma non concesso, che Terra e razzo sono due sistemi inerziali, che ne è del principio di relatività ? Non mi sento di ragionare come chi sembra sostenere la realtà dell’effetto perché  la schiacciante maggioranza dei trattati di relatività è concorde nel ritenere valida la deduzione dell’effetto dalla teoria. D’altra parte com’è possibile rinunciare a ciò che tutti i fisici quotidianamente ci dicono di dover accettare, oltre ai principi di conservazione, le sacre simmetrie ? Non sarebbe ad esempio possibile rimettere in discussione lo stesso principio di relatività ? Non credo però che quest’ultima soluzione piaccia a chi è uso schierarsi con le schiaccianti maggioranze.

NOTE

(925) Dati più completi si possono trovare in: Sexl, Schmidt – Spaziotempo – Boringhieri, 1980; Cortini –Vedute recenti nell’insegnamento della relatività ristretta – Quaderni del Giornale di Fisica 4, Vol. II, 1977; L.I. Schiff – Experimental Tests of Theories of Relativity – Physics Today, Novembre 1968; N. Calder – L’universo di Einstein -Zanichelli, 1981.

E’ POSSIBILE OSSERVARE LA CONTRAZIONE DELLE LUNGHEZZE ?

        In un lavoro del 1959 J. Terrell mostra l’impossibilità di osservare la contrazione di Lorentz. In particolare egli mostra, che un dato oggetto, in moto con velocità v molto grande rispetto ad un riferimento in quiete S, risulta, rispetto ad S, non contratto ma ruotato.

        Supponiamo di considerare un cubo di lato d’ in moto con velocità v rispetto al nostro riferimento S considerato in quiete (il moto avvenga in modo che gli spigoli del cubo si mantengano paralleli a quelli del riferimento). Per semplicità consideriamo le cose in due dimensioni, come mostrato nella figura 74 (anziché un cubo, consideriamo un quadrato). Supponiamo che il fenomeno sia

Figura 74

misurato da un osservatore T che si trova (sul piano della figura) a grande distanza (che veda cioè il quadrato sotto un piccolo angolo o, che è lo stesso, che riceva la luce proveniente dai diversi spigoli del

quadrato sotto forma di raggi paralleli). Come arriva agli occhi di S la luce proveniente dai quattro spigoli ?

        La luce proveniente da A e da B arriverà prima di quella proveniente da C e da D, infatti questi ultimi spigoli sono più distanti da T dei primi due o, che è lo stesso, la luce proveniente da C e da D che arriva agli occhi dell’osservatore è stata emessa prima di quella proveniente da A e B arrivata  agli  occhi dello stesso osservatore.

        Mentre la luce proveniente da C inizia a propagarsi, il quadrato si va spostando verso destra con velocità v. Ciò comporta che la luce proveniente da C non arriva agli occhi dell’osservatore: essa incontra sulla sua strada il lato AB del quadrato che, nel frattempo si è fatto avanti.

        La luce proveniente da D arriverà invece a T senza incontrare alcun ostacolo proprio per lo stesso motivo per cui la luce proveniente da C non arriva a T (il lato AB del quadrato si è spostato in avanti e lascia il passo alla luce proveniente da D). Quando la luce proveniente da D è arrivata all’altezza dell’asse x, avendo percorso il tragitto d = c.Δt allora la luce emessa dagli spigoli A e B parte simultaneamente a quella proveniente da D (arrivata sull’asse x) ed arriva simultaneamente agli occhi di T.

        Il quadrato apparirebbe allora a T distorto (figura 75) tanto più quanto più è grande la velocità v,

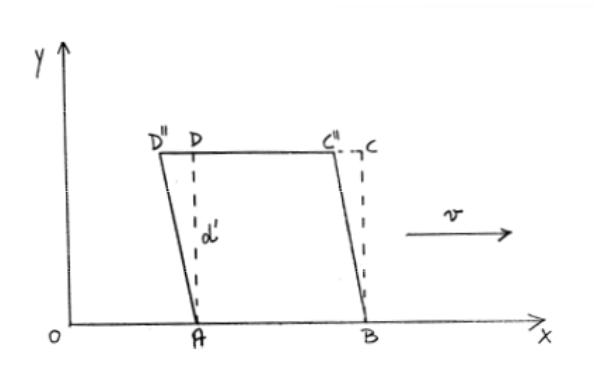
Figura 75

poiché:

(51)                                                          D”D = C”C = v.Δt              

mentre rimane sempre:

(52)                                                         d’ = DA = CB = c.Δt                 

A questo punto però occorre tener conto della contrazione di Lorentz sul lato d del quadrato in moto parallelamente all’asse x. La lunghezza d per questi lati del quadrato (AB e CD) che T misura è data da:

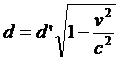
si veda, allo scopo, figura 76. Il quadrato appare così ruotato di un angolo α tanto maggiore quanto maggiore è v. Si può anche calcolare il valore di α. Poiché i tempi Δt che compaiono nelle (51) e (52) sono gli stessi, dalla (52) si ricava che  Δt =d/c. Di conseguenza la (51) diventa:

D”D = C”C = (v/c).d’

Dalla figura 76, confrontata con la 75, si vede che:

D’A = D”D                                    e                                  C’B’ = C”C

Figura 76

Di conseguenza:

(53)                                                          D’A = C’B’ = (v/c).d’

D’altra parte applicando il teorema dei triangoli rettangoli al triangolo DD’A si vede subito che:

(54)                                                                D’A = d’.sen α

Confrontando la (53) e (54) si trova che:

sen α = v/c.

Applicando poi un analogo teorema al triangolo AB’B si trova, che:

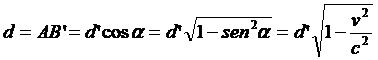
che è la relazione che già avevamo trovato.

        In definitiva un oggetto in rapido movimento appare ruotato ad un osservatore in quiete.

EQUIVALENZA MASSA-ENERGIA

        E’ appena il caso di accennare al fatto che la relazione di Einstein E  = mc²  ha avuto le più svariate conferme sperimentali soprattutto nel campo della fisica nucleare e delle parlicelle elementari. D’altra parte l’applicazione più massiccia della relatività la si ha proprio in questi campi nei quali si ha a che fare con velocità elevatissime realizzate all’interno degli acceleratori di parlicelle. Insomma la relatività ristretta è oggi una certezza della fisica o, per meglio dire, essa rappresenta una descrizione più completa del mondo naturale di quella fornitaci dalla fisica classica. Con ciò non intendiamo dire che la fisica classica sia da buttar via,  tutt’altro; questa fisica è perfettamente valida nelle approssimazioni più che legittime di v << c. Praticamente tutti i fenomeni che ordinariamente ci circondano sono classici e solo un maniaco li tratterebbe relativisticamente (ben sapendo che, anche trattandoli relativisticamente, si otterrebbero dei risultati che differiscono da quelli classici per la 12-esima o 13-esima cifra decimale e che sfidano qualunque strumento di misura).

UN ESEMPIO DI ELETTRODINAMICA RELATIVISTICA: IL CAS0 DELLA CARICA E DEL FILO CARICO IN MOTO RELATIVO.

        All’inizio del paragrafo 2 di questo capitolo, quando abbiamo cominciato a discutere l’articolo di Einstein del 1905 sulla relatività, avevamo detto che uno dei motivi che muovevano Einstein erano le asimmetrie che presentava la trattazione ordinaria dell’elettrodinamica. In particolare avevamo discusso le azioni elettrodinamiche tra due cariche elettriche, ambedue cariche positivamente, nel caso di osservatore immobile rispetto alle cariche supposte in quiete e nel caso di osservatore in moto rispetto alle cariche in quiete (si riveda la figura 42). Sull’onda di asimmetrie di quel tipo Einstein sviluppò la relatività ristretta; noi abbiamo seguito alcuni sviluppi di questa relatività, è ora doveroso andare a vedere come la relatività risolve quel tipo di asimmetrie elettrodinamiche. Ridiscutiamo quindi il fenomeno cominciando con il ridisegnarci la figura 42 in un modo leggermente differente. Supponiamo di avere due particelle dotate di una stessa carica q. Siano esse in moto con velocità u rispetto ad un osservatore T supposto in quiete. Il moto avvenga in direzioni parallele e nello stesso verso (quello positivo dell’asse x). Come ulteriore esemplificazione supponiamo poi che le due particelle abbiano la stessa ascissa x e si trovino ad una distanza r, data solo dalla differenza delle loro ordinate (figura 77a).

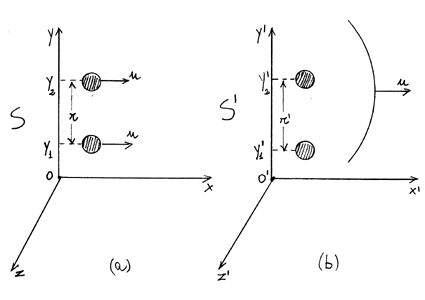
Figura 77

 Su queste due cariche agisce ima forza repulsiva dovuta alla legge di Coulomb ed una forza attrattiva dovuta alle azioni elettrodinamiche tra correnti (forza di origine magnetica). Se ora passiamo al riferimento S’ in moto con la stessa velocità u delle cariche, in questo riferimento le cariche risulteranno in quiete di modo che si dovrà sempre considerare la forza repulsiva coulombiana ma non si dovrà più tener conto della forza attrattiva di tipo magnetico (figura 77 b). E da qui proprio nasceva l’asimmetria che stiamo cercando di risolvere; possibile che le forze magnetiche siano un qualcosa che dipende dal riferimento ?

        Ebbene, quando ci troviamo su S’, dovremo considerare una forza repulsiva coulombiana, diretta lungo l’asse y’, che, come sappiamo, è data da:

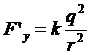
Su ciascuna carica agirà questa forza diretta in verso opposto. Per calcolare quanto vale F_y  si può far uso delle (43) tenendo conto che, come abbiamo già trovato (vedi paragrafo 2 di questo capitolo), la carica è invariante per una trasformazione di Lorentz e che, ancora le trasformazioni di Lorentz, ci assicurano ch e y = y’ e cioè Δy = Δy’ ed in definitiva r = r’. Si trova allora:

avendo osservato che F_x = F_y =0  e che F_z = F’_z (1 – u²/c²)^1/2 . Anche dal riferimento S, quindi, si osserva, una repulsione. Essa sarà più piccola del fattore  (1 – u²/c²)^1/2   rispetto a quella che si osserverà da S’. E’ importante notare che forza repulsiva minore comporta un moto di allontanamento delle cariche più lento. Quest’ultimo fatto è conseguenza diretta del fenomeno di dilatazione del tempo che da S si osserva su S’.

        Da quanto detto si possono ricavare almeno due conclusioni apparentemente diverse:

1) le forze magnetiche sono forze di origine relativistica;

2) le forze elettriche e magnetiche sono della stessa natura e tanto vale parlare di forze elettromagnetiche (i due tipi di forza sono sempre presenti e la forza elettrica è un caso particolare di forza elettromagnetica quando risulta u= 0),

        Al risultato trovato possiamo giungere anche per altra via, utilizzando le equazioni di trasformazione per i campi (14) che noi riscriviamo ora in altra forma [le inverse delle (14) introducendo il vettore B in luogo del vettore H e ponendo u in luogo di v]:

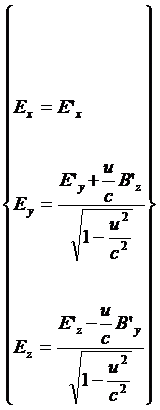
(14 bis)

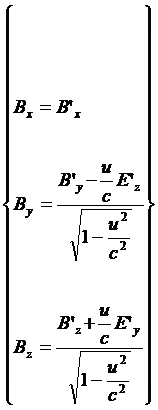
Cominciamo con il considerare i campi nel sistema S’ (figura 77 b). Poiché ora si ha solo a che fare con il campo coulombiano diretto lungo l’asse y’, si avrà:

(14 ter)

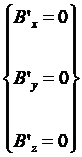
Mettiamoci ora nel sistema S ed utilizziamo le equazioni (14 bis) di trasformazione. Sostituendo i valori delle (14 ter) nelle (14 bis), si avrà:

(14 quater)

Come risultato delle trasformazioni relativistiche troviamo un risultato ben comprensibile classicamente. Quando osserviamo due cariche in moto (due correnti elementari concordi come nel caso di figura 77 a) oltre al campo coulombiano E  si genera un campo magnetico B  diretto perpendicolarmente al piano formato dalla direzione della forza e dalla direzione del campoelettrico (regola di Fleming della mano sinistra). Si osservi che B_z , in figura 77 a, è diretto lungo il verso positivo dell’asse z, perpendicolarmente alla figura.

        Il campo magnetico B_z  nasce come conseguenza delle trasformazioni relativistiche in accordo con quanto visto precedentemente.

        E questo per quel che riguarda i campi.

        La forza agente su una delle due cariche si può calcolare mediante la relazione che ci fornisce la forza di Lorentz:

Lo sviluppo di questa relazione nelle sue componenti fornisce solo quella lungo l’asse y, a seguito delle (14 quater). Si trova:

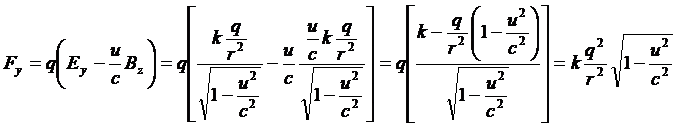
e, come si può vedere, quest’ultimo risultato è esattamente lo stesso trovato in precedenza con altro procedimento.

Categorie:Senza categoria