FEDE CONTRO SCIENZA (Parte 2)

By robertorenzetti44 on 14 agosto 2020 • ( 0 )

Roberto Renzetti

(Ottobre 2009)

PARTE II

RICOMINCIO DA JAKI (PRIMA DI DISCUTERE DI COSE SERIE)

Poiché Stanley Jaki è un riferimento costante per i cattolici della parrocchietta e poiché Jaki, a parte le sciocchezze proprie, dal punto di vista dei riferimenti culturali, ha solo Duhem, è necessario parlare un poco di Jaki per poi passare ai pezzi forti di Duhem.

Per parlare di Jaki basta riferirsi ad una intervista rilasciata ai nuovi carnefici di Totus Tuus, Cosimo Baldaro e Cosimo Galasso, riguardante Giordano Bruno. In essa Jaki fa sfoggio della sua ignoranza. Si legga il link proposto, qui riporto solo sue perline:

Dice Jaki – Bruno non ha nulla a che vedere con la scienza. Nella Cena delle Ceneri non vi è alcuna traccia di scienza, ma addirittura il suo contenuto rappresentava un insulto a Copernico e alle sue concezioni. Bruno non vuole sostituire le rovine dell’universo aristotelico-tolemaico con la precisione dell’universo copernicano e del suo strumento, la geometria. Bruno distrugge, affinché la confusione e l’imprecisione possano regnare. In definitiva Bruno vuole solo distruggere.

Jaki ha forse letto la Cena delle Ceneri ma non ha capito un tubo. In questa magistrale opera Bruno, prima addirittura di Galileo, formula i Principi d’Inerzia e Relatività, estendendo quest’ultimo addirittura alla dinamica (si vada a leggere Il contributo di Giordano Bruno alla nascita della “nuova fisica”: i principi d’inerzia e di relatività nella sua opera che si trova nell’ultimo paragrafo del link indicato). E’ poi ridicolo che uno che è vissuto solo su Oresme e Buridano che sguazzano in Aristotele venga a dare giudizi da inquisitore su Bruno che rompe il mondo molto di più di quanto non lo abbia fatto Galileo. Ma poi questo personaggio noto solo ai frequentatori della curia, cosa sa dell’ambiente filosofico-magico del Cinquecento italiano ed europeo. Il Bruno che vuole distruggere è patetico perché è impossibile leggerlo per quello che è. Egli distrugge perché il mondo di Aristotele i cui rappresentanti sono Papa, Cardinali e gerarchie ecclesiastiche era ed è marcio era finito e chiuso su ogni novità prorompente da tutte le parti. La stessa accusa di magia a Bruno, mostra completa ignoranza dello svolgersi degli avvenimenti e particolarmente della Chiesa.

Utilizzare oggi delle frasi ad effetto su chi poco sa sulle questioni rinascimentali e barocche, può risultare squalificante. Questa è l’operazione che generalmente si fa con Bruno ed essa ha successo per il facile impatto distruttivo che ha sulle persone alle quali mi riferivo. Si usa dire che Bruno era, di volta in volta o simultaneamente: un animista, un ermetico, un mistico, un mago, un filosofo. Si vanno a cogliere tra i suoi scritti frasi che, pur non essendo rilevanti nel contesto, sono oggi da giudicarsi prive di senso. La stessa operazione non viene mai fatta, soprattutto dalla storiografia anglosassone ed anche francese su studiosi, filosofi o scienziati dei rispettivi Paesi.

Questo aspetto richiederebbe un’ampia trattazione (si veda il lavoro, presente nel sito, Magia, Religione e Scienza nel Rinascimento italiano) anche perché le citazioni dalle opere originali sono lunghe. Qui mi accontento di riassumere qualche posizione, assolutamente comprensibile data la epoca, ma che se fosse stata sostenuta da Bruno lo avrebbe fatto squalificare ancora di più. Riferiamoci solo ai personaggi più noti.

Copernico: Essendo il Sole l’occhio di Dio è più logico che sia sistemato al centro dell’universo.

Kepler: Il Sole è il corpo più bello e come tale è occhio del mondo. Esso è l’unico luogo degno di diventare la casa di Dio se questi si degnasse di venire tra noi. Dio poi ha creato ed ordinato l’universo secondo le armonie e le proporzioni dei cinque solidi regolari di Pitagora e Platone. I pianeti poi nel loro moto intorno al Sole cantano le lodi del Signore. Ad esempio la Terra canta mi-fa-mi e per questo non possiamo stupirci del fatto che sulla Terra regnino MI-seria, FA-mine, MI-seria. Osservo a parte che fino ad un certo punto Kepler fu fortunato. Ai suoi tempi i pianeti conosciuti arrivavano fino a Saturno. In questo modo numero di pianeti (5) e numero di solidi regolari (5) gli fecero costruire una montatura teorica le cui proporzioni tornavano. Il guaio è che i solidi regolari sono ancora 5 mentre i pianeti sono cresciuti di numero. Tra l’altro Kepler ebbe un sussulto quando seppe che Galileo aveva scoperto i satelliti di Giove e si chiese ad alta voce se per caso Bruno non avesse avuto ragione.

Descartes: La quantità di movimento si conserva perché Dio mai toglie ciò che ha dato. Osservo a Margine che Padre Marsenne maestro di Descartes (oltreché di Pascal, che aiutò nel plagio di Torricelli) disse di Bruno (1624): “È uno dei più abominevoli uomini che la terra abbia mai avuto”.

Newton: I pianeti continuano nel loro moto infinito intorno al Sole per il continuo intervento di Dio che, di tanto in tanto gli fornisce “una spintarella”. Egli fu un mago, un alchimista ed un teologo bigotto.

È utile osservare che tutti i citati facevano oroscopi (per arrotondare). Mai né Bruno né Galileo hanno fatto oroscopi nonostante ne fossero richiesti, soprattutto il secondo, in cambio di grosse ricompense (Galileo è sempre stato per tutta la vita persona piuttosto legata al denaro: gli mancava sempre).

Jaki afferma che l’universo copernicano era ordinato mentre Bruno voleva il disordine (infiniti mondi, infiniti soli, senza confini, un mondo infinito, …). Il mondo di Copernico era una grandissima confusione di mescolanze tra concezioni aristoteliche e vere novità. Tale mondo non poteva esistere. Iniziò a farlo con Galileo. Ora spiego ai suoi seguaci perché il mondo di Copernico era un assurdo filosofico e scientifico. Entriamo ora in un campo che è stato discusso infinite volte e, anche se i chierichetti non leggeranno, occorre ripetere. Ciò che segue riassume i termini della questione. La tesi centrale dell’opera di Copernico, il De Revolutionibus Orbium Coelestium, la Terra in moto intorno al Sole immobile, rappresentò una svolta radicale ma più per le conseguenze che altri ne trassero che non per quello che lo stesso Copernico aveva detto. Egli, partendo da dati osservativi e per rispondere al vecchio problema del moto della sfera delle stelle fisse (tale sfera era considerata da Aristotele in moto pur occupando sempre lo stesso luogo), modificò le posizioni degli astri nel sistema astronomico aristotelico-tolemaico, senza preoccuparsi di conciliare ciò con tutti gli altri problemi che si aprivano con la nuova organizzazione planetaria. I ragionamenti che Copernico porta a sostegno della tesi che vuole la Terra in moto intorno al Sole immobile sono aristotelico-scolastici. Seguiamo questi ragionamenti:

– “Poiché il cielo è la dimora di tutti …, non si vede perché non si debba attribuire il moto più al contenuto che al contenente”.
– Se la Terra a causa del suo moto dovesse andare distrutta, a maggior ragione si dovrebbe distruggere la sfera delle stelle.
– La Terra non va distrutta a seguito del suo moto perché esso è naturale e non violento.
– La caduta non lungo la verticale che dovrebbero avere gli oggetti è spiegata con
l’affermazione che l’aria segue il moto della Terra “perché l’aria, impregnata di terra e di acqua, vicina alla terra, segue le sue stesse leggi”.
– “La condizione di immobilità è considerata [da Aristotele] più nobile e divina della condizione di cambiamento ed instabilità, la quale quindi è più appropriata alla Terra che all’Universo”.
– Ci vorrebbe un motore enorme per muovere la sfera delle stelle.
– La Terra deve ruotare di moto naturale perché è sferica.

Queste argomentazioni di Copernico creano moltissime difficoltà allo stesso aristotelismo e mostrano forzature dei ragionamenti. Se non sapessimo che Copernico è persona dottissima potremmo addirittura dubitare della sua conoscenza di Aristotele. Vediamo allora le difficoltà nei ragionamenti di Copernico.

– Ha ragione Aristotele quando afferma che la Terra dovrebbe disintegrarsi a causa del suo moto e non la sfera delle stelle. Infatti la Terra è soggetta a generazione e corruzione oltre a possedere pesantezza, mentre la sfera delle stelle è eterea, eterna e per essa non esiste pesantezza.
– Allo stesso modo, un motore avrebbe mosso più facilmente le parti eteree dell’universo che non la Terra.
– Anche il Sole è sferico e perché dovrebbe essere immobile ? – Il sistema infine, anche se nasceva dal proposito di rendere più semplici i calcoli, era complesso almeno quanto l’aristotelico-tolemaico.

Nonostante il “conservatorismo” di Copernico, si aprivano grosse brecce nel sistema di Aristotele che qualcuno avrebbe dovuto sistemare se avesse abbracciato il nuovo sistema e questo perché, come ho ricordato più volte, il sistema astronomico aristotelico-tolemaico è un tutt’uno con la fisica di Aristotele. E’ impensabile modificare un pezzo dell’impianto senza rendersi conto dei guasti nell’altro. Vediamo quali erano i problemi che si aprivano e che, al momento, erano senza soluzione:

– Si mette in discussione l’esistenza di due tipi di mondi separati dal cielo della Luna (la Terra, nel suo moto, “si infila” in mezzo ai due mondi).
– Si distrugge la teoria dei quattro elementi e quella del moto ad essa collegata tramite la teoria dei luoghi naturali (perché ora un oggetto dovrebbe cadere sulla Terra?).
– Tutti i moti vengono considerati come naturali e la Terra che si muove di moto circolare viene a perdere le caratteristiche di peso e leggerezza.
– Con l’ammissione di immobilità dell’ultima sfera (quella delle stelle fisse), in accordo con Aristotele (l’infinito non può muoversi), si apre alla possibilità di un mondo “infinito”.

Per dirla con Kuhn: Per Copernico la Terra in moto rappresenta un’anomalia in un universo aristotelico. Ed ora se i chierichetti non hanno capito il gran casotto fatto da Copernico, non hanno speranza. Quindi Bruno coglie la grande novità della rottura del mondo aristotelico (rottura e basta) ed immagina di andare oltre togliendo ogni altra barriera. Questo è pensiero e non come dice un benedettino per scherzo Bruno non è certamente un martire della scienza e neppure del libero pensiero, a meno che per “libero pensiero” non s’intenda “pensiero a ruota libera”. Lo scopo di Bruno consisteva nel promuovere una visione del mondo impregnata di misticismo occultista e magico. Il suo interesse per la teoria copernicana aveva soltanto lo scopo di promuovere la visione di un nuovo ordine del mondo basato sull’occultismo. Purtroppo, perfino gente con un elevato grado di cultura crede ancora che Bruno abbia serie credenziali scientifiche. Altrimenti, per esempio, perché organizzare, presso l’università La Sapienza di Roma, un convegno internazionale dal titolo Giordano Bruno e la nuova scienza, al quale, il giorno 18 febbraio 2000, sono stato invitato come relatore? Soffermatevi su questo rosario di sciocchezze e coniugatele con il dialogo scienza e fede. Capirete che con questi personaggi non c’è dialogo perché il dialogo presuppone due entità pensanti e da quella parte difetta tutto il pensiero. Riguardo alla magia e l’occultismo debbo ancora rimandare all’articolo già citato ed aggiungere che in quell’epoca i papi riconobbero ufficialmente magie, alchimie ed oroscopi. Uno tra i più strenui difensori della magia ermetico-cabalistica e di ogni pratica astrologica ed alchemica fu Alessandro VI (Papa dal 1492 al 1503). In una sua lettera a Pico della Mirandola (ed anche in una Bolla che Pico pubblicò nei frontespizi delle sue opere “magiche”) la magia veniva in qualche modo riconosciuta come un sostegno al cristianesimo. Fu la Chiesa quindi che si innamorò della magia quella Chiesa che oggi ha avuto Milingo ed esorcisti vari tra cui Padre Amorth (omen nomen), quella Chiesa che negli USA ha pedofili in quantità industriale (è fuori tema come sono fuori tema molte osservazioni dello “storico” su Bruno). La magia all’epoca si suddivideva in due rami principali che erano: quella naturale e quella nera. La seconda è quella che ancora oggi conosciamo come magia. La prima era invece lo studio della natura ed in nuce aveva in sé le caratteristiche di quelli che quasi contemporaneamente saranno conosciuti come filosofi naturali. Come si può ben comprendere fu però la posizione della Chiesa che fece crescere enormemente gli influssi in ogni campo di magie, alchimie, astrologie e cabale. Ma poi queste continue operazioni di buttare là frasi ad effetto senza minimamente preoccuparsi di capire in che epoca si è fa parte del vergognoso bagaglio dei venditori ambulanti o degli ignoranti sempre e comunque schierati alla corte dei potenti. Jaki non è sazio di baggianate e continua imperterrito affermando che dovunque in Europa Bruno avrebbe avuto la stessa sorte (questi brucerebbero ancora chi dissente, senza alcun problema): rimane il fatto che il distacco di Bruno dall’ortodossia cristiana era così ampio e profondo, che lo stesso destino gli sarebbe stato riservato sia nella “repubblica teocratica” costruita nell’elvetica Ginevra da Jean Cauvin — italianizzato in Giovanni Calvino (1509-1564) — che nell’Inghilterra di Elisabetta I Tudor (1533-1603), se fosse rimasto in entrambe per lo stesso lasso di tempo. A Ginevra viene scomunicato dal Concistoro calvinista, e sarebbe stato immediatamente arrestato, se non fosse sfuggito alla presa della teocrazia calvinista il più velocemente possibile. La risposta al fratacchione è: Ma a Venezia no. Solo i ricatti della Chiesa hanno permesso ciò che poi è accaduto, l’orrendo massacro. E stupisce ancora la via della giustificazione dell’ineluttabile. Neppure sfiora il cervello di questi infami che si può pensare in modo diverso (questo è il libero pensiero che chi ha la pancia piena dei soldi dei cittadini, senza colpo ferire, non può capire). Ma poi, secondo lo storico, una persona che non sa sostituire tutto un impianto nuovo al vecchio che pur ordinato crolla, non ha diritto di parola? Caspita ! E che visione viene proposta ? quella di Bellarmino che era certamente ordinata? Certo è deprecabile, come dice carognescamente Jaki, che Bruno sia finito al rogo, ma l’astio profondo, l’odio nei suoi riguardi non cessa se tutto è incentrato su quella sola “piccola parte” (la parte scientifica) di contributo di Bruno che pur viene ammessa dallo stesso “storico”. L’astio è ancora legato a quella montagna di eresia, grandissima parte del suo pensiero, che gli viene di nuovo rinfacciata e per quella si mescola indegnamente nella parte scientifica. Così Jaki può concludere che comunque qualcuno lo avrebbe ammazzato per giustificazione non benedettina ma gesuita. La storia del Congegno alla Sapienza di Roma è popi esemplare della chiusura ed ottusità del personaggio. Perché organizzare un convegno su “Giordano Bruno e la nuova scienza“? Quando si organizzano convegni in un Paese civile e laico, Jaki, le tesi finali non sono date a priori come accade nelle riunioni dogmatiche ecclesiastiche. Alla fine di un tale convegno, si potrebbe anche concludere che Bruno con la nuova scienza non c’entra nulla. Non risulta a tale storico questo modo di procedere? Ma qui si misura anche il grado di ignoranza di Jaki. Non sa neppure cosa vuol dire “nuova scienza” o “scienza nuova”. Non conosce neppure Vico il nostro storico, non conosce il valore epistemologico di Scienza Nuova nel ‘500 italiano, che non è come dire nel ‘500 russo.

Jaki poi vuole dare l’immagine di uno che conosce sia la geometria di Copernico sia la fisica avanzata. Ed accusa Bruno di non conoscere neppure la geometria.Bruno non conosceva la geometria che utilizzava Copernico? Possibilissimo ma ciò cosa vuol dire? Chi non conosce tale geometria non può discutere delle conclusioni copernicane? Chi lo avrebbe potuto fare ? il noto geometra Bellarmino ? o il noto forcaiolo Papa Barberini ? Ha provato lo storico Jaki a leggersi i “Principia Mathematica” di Newton con il metodo delle flussioni, una sorta di analisi matematica costruita come una geometria ? Ho fortissimi dubbi ma se qualche seguace vuole possiamo parlarne. A proposito, che dicono i jakisti dei metodi “geometrici” di Tolomeo? Quelli li conoscono ?

Andando oltre Jaki disquisisce sull’infinito di Bruno dicendo che la cosa non ha senso perché nessuno dei contemporanei, fino a Newton, ammetteva l’infinito (non può mancare l’errore perché il mondo per Galileo non è finito come dice Jaki ma interminato). Caspita ! L’infinito per alzata di mano. Stupenda logica quella del fratacchione. Ed arriva a ciò che in questi personaggi non può mancare, ai creatori della scienza moderna secondo Duhem, che sarebbero Oresme e Buridano: Nel Medioevo l’ipotesi dell’eternità dell’universo, presente nella cosmologia greca, viene abbandonata in considerazione del dogma cristiano della creazione ex nihilo et in tempore. Questo mutamento comporta, in particolare, una sostituzione delle leggi aristoteliche del moto con la legge del moto inerziale formulata dai filosofi e teologi scolastici francesi Jean Buridan, italianizzato in Giovanni Buridano (1300 ca.-1360 ca.), e Nicole d’Oresme (1323-1382), fatto di grande aiuto per Copernico e per i suoi primi seguaci. Un altro grande contributo dei medioevali alla scienza newtoniana è l’invenzione dell’ars latitudinis, ovvero dell’uso delle dimensioni geometriche per rappresentare le grandezze fisiche. Essa è basilare per lo sviluppo successivo della geometria analitica da parte del filosofo e matematico francese René Descartes, italianizzato in Renato Cartesio, (1596-1650) e aiuta Galileo nel calcolare che le distanze coperte dai corpi in caduta libera sono proporzionali al quadrato del tempo. Pertanto, se il mondo moderno ha una scienza, lo deve alla cultura della Cristianità medioevale.

Sui contributi degli Oresme e Buridano parlerò più diffusamente nel prossimo paragrafo, ora dico poche cose. Gli studiosi di Oxford sono passati alla storia per le loro controversie di tipo aristotelico, controversie dalle quali Bruno è sempre rifuggito inorridito. Esempi di controversia aristotelica (si badi bene: aristotelica, non di Aristotele): il cioccolato è un cibo liquido o un cibo solido ? Che utilità potrebbe avere per l’uomo avere un dito in più o un dito in meno ? Visto che occorre tagliarsi le unghie è conveniente iniziare dalla mano destra o dalla sinistra ? Ma poi, nonostante estenuanti ricerche, nulla risulta del contributo di sì raffinati critici alla nascita della scienza moderna. Ingiurie? Molto poco in un’accolita di aristotelici ! Inoltre la frase che vorrebbe la legge del moto inerziale ricavata da Oresme e Buridano è esemplificativo dell’ignoranza di Jaki. Il moto inerziale formulato dagli scolastici ? Certo qui non vi sono alternative alle seguenti: o Jaki è un imbroglione o è un ignorantone. Insisto le scuole di Oxford e di Parigi, generalmente di francescani, hanno avuto un qualche rilievo da pochi anni quando storici seri si sono accaniti a ricercare i loro contributi. Ma qualunque studioso serio, non solo della scienza, sa che tutti i contributi che non sono stati riconosciuti e non hanno avuto ricadute sono uguali a zero, dal punto di vista dell’influenza sull’evoluzione del pensiero. L’esempio italiano che si può fare è quello di Leonardo. Non ha avuto scuole, scriveva in modo che si capiva da solo, inutile ricercarne una scuola, una influenza se non in ambiti pubblici come la pittura, pur infelice dal punto di vista della tecnica, almeno degli affreschi.

Aggiungo poi che quell’italianizzato che usa Jaki è una bufala. I nomi di scienziati-filosofi citati non sono “italianizzati” come atto tipico degli statunitensi o degli ispanici, quasi una forzatura di una volontà di imporre la propria lingua. In realtà erano gli stessi personaggi citati che si “latinizzavano” (non “italianizzavano”) firmando le loro opere. Così Descartes si firmava Cartesius, Kepler si firmava Keplerus e così via. Il fatto è che l’Italia, all’epoca era il centro mondiale della ricerca scientifica finché non intervenne la mannaia della Chiesa che, nell’arco di qualche anno riuscì a spostare il baricentro della ricerca nel Nord Europa. Da allora (condanna di Galileo) in Italia vi sono stati 300 anni di buio (fino ad Enrico Fermi ed alla sua scuola).

Alla fine dell’intervista il fratacchione fa sfoggio di conoscenze di fisica contemporanea dicendo un mare di sciocchezze. Che c’entra la massa totale dell’universo con la sua finitezza o infinità? Che confusione Jaki! La massa può essere finita in un mondo finito o infinito! Ma poi si rilegga (se lo ha mai fatto) Einstein e si accorge che lei continua ad errare gravemente. La fisica non è né fede né dogma. Non è vero che, una volta stabilito che la massa è finita è indifferente che lo spazio sia finito o infinito. Non ha mai sentito parlare del continuo spazio temporale ? Che lo spazio assoluto ed indifferente alla Newton non c’è più, pur avendo assolto un ruolo importantissimo?

Insomma, leggetevi questo pezzo di ignoranza e capirete certamente da soli. E su Jaki non torno più. Quando lo citerò ricordatevi della montagna di nulla che è questo personaggio citatissimo dai bigotti tradizionalisti della curia.

Ed ora passiamo a cose serie che vorrebbero essere base di studio per i suddetti clericali ottusi. Una discussione che abbia un qualche senso e che riguarda anche scienza e fede deve partire dal conoscere cosa si discute, altrimenti facciamo le disquisizioni aristoteliche che tanto amavano i chierici medioevali.

CORRENTI FILOSOFICHE E SCIENTIFICHE SUL FINIRE DEL MEDIOEVO

        Nonostante già si conoscessero alcune opere di Aristotele, l’intero corpo dei suoi lavori, che rende ben conto della complessità, globalità e sistematicità del suo pensiero, viene conosciuto nel corso del XII secolo. E’ il primo sistema che abbraccia nel suo complesso tutte le branche del pensiero e della conoscenza. Il fascino che l’aristotelismo iniziò ad esercitare fu enorme. Anche tra i cristiani (particolarmente quando gli Scolastici conobbero la Metafisica di Aristotele) sorse un forte moto di ammirazione: il sistema aristotelico poteva rappresentare il complemento filosofico, ciò che la Chiesa aveva sempre cercato, al Cristianesimo stesso, un corpo di dottrine che avrebbe finalmente culturalmente nobilitato il Cristianesimo (che, fino ad allora, si era affidato alle pie ma parziali visioni di Platone e dei neoplatonici). Sfortunatamente in Aristotele, più che in Platone, mancava l’idea di Dio. Questo fu il motivo per cui l’aristotelismo ebbe alterne vicende agli inizi del 1200. Intanto, già nel 1169, il Concilio di Tours aveva vietato ai monaci di leggere i pericolosi testi di fisica. Nel 1210 il Concilio provinciale di Parigi vieta l’insegnamento delle dottrine di Aristotele. E non è che queste cose non avessero peso. Ormai le Università non erano più le libere Università dei felici momenti in cui nascevano; vista la loro crescente importanza queste, con il beneplacito ed il sostegno delle varie case regnanti, erano ormai passate tutte sotto il controllo diretto della Chiesa (principalmente erano gestite da francescani e domenicani). I divieti di insegnamento o le condanne avevano effetti immediati sulla diffusione, ai livelli culturali più elevati, delle dottrine di Aristotele e degli aristotelici. Inoltre, proprio all’inizio del XIII secolo cominciarono a diffondersi per l’Europa svariati movimenti religiosi giudicati eretici dalla Chiesa. Tra questi i principali erano: i Catari (Albigesi, Manichei, Patarini, …) ed i Valdesi. Nel 1209, una «crociata» contro gli Albigesi si era conclusa con orrendi massacri. Ma l’aspetto più importante di ciò è che nel 1233 Gregorio IX fondò il Tribunale della Inquisizione che (1235) venne affidato come privilegio ai Domenicani e poi esteso ai Francescani [si iniziò subito con la pratica della tortura che fu ufficialmente autorizzata e riconfermata da successivi Papi: Innocenze IV (1252), Alessandro IV (1259), Clemente IV (1265)]. Ebbene, in questo clima, si susseguirono altre condanne ad Aristotele: dapprima si espresse in proposito il Concilio lateranense del 1215 (Papa Innocenzo III), quindi la condanna fu riaffermata da Papa Onorio III e successivamente da Papa Gregorio IX (1231), infine, qualche anno dopo, da Papa Urbano IV. Ancora nel 1277 sia. il Vescovo di Parigi che quello di Canterbury condannarono la quasi totalità dell’opera di Aristotele e degli aristotelici (essenzialmente Averroé). Da notare che i più accaniti contro Aristotele (forse sarebbe meglio dire contro l’aristotelismo) furono i francescani.
        Il contrasto tra aristotelismo e Cristianesimo (insignificanza del posto di Dio, eternità del mondo con conseguente negazione della Creazione, inesistenza di libero arbitrio in un mondo determinato dal movimento delle sfere celesti, …) fu appianato da San Tommaso che semplicemente corresse Aristotele dove questi risultava in contrasto con le dottrine della Chiesa (l’interpretazione averroistica di Aristotele – negazione dell’anima individuale – continuava ad essere in forte contrasto con la Chiesa). Solo quattro anni dopo la morte di San Tommaso, nel 1278, i domenicani assunsero ufficialmente la dottrina di San Tommaso che piano piano divenne la dottrina ufficiale di tutta la Chiesa (la cosa fu ratificata da Papa Pio V che, nel 1567, in piena Controriforma, nominò Tommaso Dottore della Chiesa). Fu così che Aristotele iniziò ad essere considerato addirittura un precursore di Cristo nelle cose naturali e quindi ad essere considerato una indiscutibile autorità nelle questioni filosofiche, scientifiche e teologiche (soprattutto per merito degli insegnamenti nelle varie Università di domenicani e francescani). Ma, fatto di maggior importanza, San Tommaso è convinto che non vi sia nessuna contraddizione tra scienza e fede di modo che incita a studiare la scienza perché ciò serve a consolidare la formazione religiosa e a sradicare errori e superstizioni. La scienza a cui si fa riferimento è una scienza empirica poiché il modo che noi abbiamo di conoscere è fondamentalmente legato ai nostri sensi, all’esperienza che loro fanno durante la nostra vita.
        Nonostante questa apertura, la scienza non decollava per svariati motivi. In primo luogo San Tommaso e gli altri pensatori come Alberto Magno erano lontanissimi dal livello culturale della quasi totalità della gente; in secondo luogo l’insegnamento medioevale era centrato quasi esclusivamente sullo studio dei classici, ispirando rispetto per la loro autorità; in terzo luogo l’illimitata venerazione di cui godeva Aristotele non permetteva passi in avanti sostanziali; infine, e questo è un aspetto molto importante, da una parte non si disponeva di una adeguata conoscenza della matematica (che si avrà solo nel Cinquecento) e dall’altro nessuno pensava ad intersecare processi di misura con la conoscenza della natura (non è la quantità che ci permette di conoscere l’Essenza delle cose). Vi era una cosa che sembra estranea a quanto discutiamo ma ha un peso essenziale: le condizioni socio economiche non richiedono e non possono permettersi scienza. In questa situazione la scienza non poteva essere altra cosa che una descrizione ingenua della natura accompagnata da una classificazione qualitativa di oggetti e fenomeni per le quali cose l’unica dimostrazione necessaria, era il ragionamento (che aiuta nella classificazione) e quindi il sillogismo (si noti che per Aristotele anche una dimostrazione geometrica era una classificazione). Inoltre la stessa organizzazione oligarchica dello Stato può essere vista come giusta in quanto gerarchizzata e quindi costruita ad immagine della natura (ciò faceva molto piacere ad ogni potente).

LA SCIENZA NEL MEDIOEVO

Un primo studioso d’interesse che incontriamo nel deserto che circondava la conoscenza è Giovanni Filopono di Alessandria (circa 490 – 570). Egli è uno dei tanti commentatori di Aristotele che opera nell’Impero bizantino come direttore della Biblioteca. E’ un neoplatonico convertito al cristianesimo che trasformerà la scuola di Alessandria in una sorta di scuola di teologia e che sarà però condannato dalla Chiesa (681) per eresia (aveva inteso la Trinità come tre persone distinte!). Egli va ricordato perché, nel suo commentare Aristotele, quell’Aristotele che arrivava in lettura platonica, mostra che alcune cose non gli tornano. Per risolvere le quali avanza una teoria, quella dell’impetus, che avrà grande importanza nel XIV secolo.

La critica di Filopono ad Aristotele è radicale e per capirla occorre riprendere alcune concezioni di Aristotele sullo spazio, il tempo ed il luogo.

   L’universo aristotelico essendo finito e tutto pieno non prevede l’esistenza del vuoto. Ciò vuol dire che al di là dell’ultima sfera non vi è alcuna cosa, neppure il vuoto. Cerchiamo ora di vedere quali sono le motivazioni che Aristotele porta all’impossibilità dell’esistenza del vuoto all’interno della sfera delle stelle fisse.

      Poiché il vuoto, se c’è, deve essere in qualche luogo e poiché il luogo è definito quando è occupato da un corpo (o più in generale da materia), è assurdo pensare alla sua esistenza essendo il vuoto, per sua definizione, assenza di corpo e di materia.

       Ci sono poi alcuni che credono nell’esistenza del vuoto in quanto esiste il movimento ma, osserva Aristotele, “non è possibile che neppure un solo oggetto si muova, qualora il vuoto esista“.

       Infatti se ci riferiamo ai moti che avvengono naturalmente in natura (i “moti naturali”, quelli rettilinei che procedono dall’alto verso il basso o dal basso verso l’alto), come è possibile che essi accadano o nell’infinito o nel vuoto, se sia infinito che vuoto non hanno luoghi particolari verso cui una cosa possa muoversi (come per esempio il fiume verso il mare, il fuoco verso l’alto, la terra verso il basso,…)? Se ci riferiamo invece ai moti violenti, ebbene, un sasso lanciato continua nella sua corsa

“perché l’aria, spinta, spinge a sua volta con un moto più veloce di quello spostamento del corpo spinto in virtù del quale il corpo stesso viene spostato verso il suo proprio luogo“.

E’ quindi l’aria che permette l’esistenza di un moto; è l’aria infatti che sostiene una freccia lanciata e che, chiudendosi dietro di essa, la sospinge.
Dice poi Aristotele nel De Coelo:

“…al di fuori del cielo non c’è, né è ammissibile che venga ad essere, alcuna mole corporea; il mondo nella sua totalità è dunque formato di tutta la materia propria ad esso… cosicché… questo cielo è uno, e solo, e perfetto.

E’ insieme evidente anche che fuori del cielo non c’è né luogo, né vuoto, né tempo. In ogni luogo infatti può sempre trovarsi un corpo; vuoto poi dicono essere ciò in cui non si trova presente un corpo, ma può venire a trovarsi; tempo infine è il numero del movimento, e non c’è movimento dove non c’è un corpo naturale“.

Da questo branorisulta che l’intero spazio concepibile da Aristotele è all’interno dell’ultima sfera, quella delle stelle fisse. Anzi per essere più precisi esso è all’interno della superficie interna dell’ultima sfera. Dice Aristotele, che usa il termine luogo invece del nostro spazio:

“…il luogo è il primo immobile limite del contenente“.

E siccome il contenente è l’ultima sfera essa è il limite del luogo. Inoltre l’esistenza del luogo rende possibile il moto:

“il più comune e fondamentale movimento, quello che si suol chiamare spostamento, è in relazione ad un luogo“.

D’altra parte l’evidenza naturale di movimenti rende plausibile l’esistenza del luogo:

“Che il luogo esista sembra risultare chiaro dallo spostamento reciproco dei corpi“.

E poiché un luogo è definito dalla presenza di un corpo, allora:

“sarebbe lecito supporre che il luogo sia qualcosa che prescinde dai corpi“.

Ed inoltre:

“…è difficile determinare che cosa esso sia, se una massa corporea o qualche altra natura… Comunque, esso ha tre dimensioni: lunghezza, larghezza e profondità, le stesse da cui ogni corpo è determinato. Ma è impossibile che il luogo sia un corpo, perché allora in esso stesso ci sarebbero due corpi“.

In definitiva, poiché l’ultima sfera, quella delle stelle fisse, si muove e poiché il movimento è possibile là dove c’è un luogo, allora:

“anche il cielo, anzi esso più di ogni altra cosa, è in un luogo, poiché il cielo è sempre in movimento”.

Se uno però sta un poco attento al legame esistente tra queste affermazioni, si accorge che esiste almeno una incongruenza. Poiché infatti il movimento, inteso come spostamento, è definito da Aristotele come l’occupare successivo di luoghi diversi, se non c’è luogo al di là dell’ultima sfera, com’è possibile che essa ruoti? E d’altra parte, essendo la Terra immobile, essa (ultima sfera) ruota.

Questa difficoltà era ben presente in Aristotele il quale, per conciliare l’inesistenza di qualunque cosa (anche il vuoto) al di là dell’ultima sfera, con il fatto che essa ruota (dovendo perciò occupare luoghi diversi) è costretto ad ammettere che l’ultima sfera, pur ruotando, occupa sempre lo stesso luogo:

“…ciò che si muove in circolo non può mutar di luogo“.

Evidentemente questo è il punto più debole della teoria aristotelica di luogo e di moto e proprio su questo punto si inserisce la critica di Filopono.

Secondo Filopono c’è innanzi tutto da rimettere in discussione la teoria del movimento di Aristotele. Se si lancia un proiettile

“è necessario che una certa potenza motrice incorporea sia ceduta al proiettile dallo strumento che lo lancia; l’aria non contribuisce affatto a tal moto, e vi contrasta ben poco…“.

    Questa formulazione, che anticipa teoria dell’impetus, fa a meno del mezzo per giustificare il movimento e considera una sorta di potenza motrice che si trasferisce da ciò che provoca il moto al proiettile che lo subisce. La fine del moto avviene per consumazione progressiva di questa potenza motrice a causa, tra l’altro, del fatto che l’aria oppone al moto una resistenza (questo almeno per quanto riguarda i moti provocati, quelli che non hanno origine naturale). Ma poiché il moto è legato al luogo, è necessario considerare cos’è il luogo. E qui viene fuori il punto più delicato della discussione: si tratta essenzialmente dello scoprire una profonda contraddizione nella definizione aristotelica di luogo. Abbiamo già visto che per Aristotele “luogo è il primo immobile limite del contenente“. Ebbene per quello che ora ci serve occorre puntare l’attenzione su quell’immobile. Infatti la questione che, ad esempio, si pone è: qual è il luogo di un sasso poggiato nel letto di un ruscello? Il corpo contenente è l’acqua, per cui ad un certo istante uno potrebbe pensare che è la superficie interna dell’acqua avvolgente il sasso che costituisce il luogo del sasso.

       Ma l’istante successivo “quel luogo” si è spostato facendo posto ad un “altro luogo”. La pietra non si è mossa, essa è rimasta là ma il presupposto suo luogo cambia istante per istante. E’ chiaro che bisogna riferirsi allora a quell’immobile di qualche riga più su. Il luogo della pietra non è altro infatti che il letto del fiume su cui è poggiata. E fin qui tutto torna. Ma se applichiamo la definizione aristotelica di luogo alle sfere celesti troviamo la contraddizione di cui si diceva. Certamente il luogo del mondo sublunare è delimitato dalla superficie interna della sfera della Luna ma essa ruota e quindi si muove e quindi non può delimitare un luogo.

     Aristotele aveva però ben presente questa difficoltà tanto è vero che per lui un moto rotatorio attorno ad un centro o ad un asse fisso, poiché la sfera occupa sempre lo stesso luogo, non è da considerarsi moto locale. Filopono prende invece in esame una zona particolare di una sfera in rotazione ed osserva che questa zona occupa successivamente luoghi diversi. E’ facile concludere allora che l’intera sfera pur restando, per così dire, nello stesso luogo, occupa sempre luoghi diversi (essendo dotata quindi di moto locale).

     Rimane allora il problema: qual è il luogo del mondo sublunare? Esso non è il cielo della luna ma non può certamente esserlo il cielo di Giove o Saturno o qualunque altro cielo perché si muovono. In particolare neanche il cielo delle stelle fisse può delimitare un qualche luogo proprio perché anch’esso non è immobile. Inoltre se ci ponessimo la domanda del qual è il luogo in cui si muove questo cielo, dovremmo ammettere di non essere in grado di rispondere poiché non sappiamo in quale luogo esso sia non essendo noi in grado di trovare alcun “primo immobile limite” di un qualche cosa che lo contenga. D’altra parte il fatto che l’ultima sfera sia dotata di moto locale implica che anche la superficie esterna di essa occupi successivamente luoghi diversi che debbono però esservi per poter, appunto, essere occupati. E’ qui evidente che comincia a traballare l’affermazione aristotelica dell’inesistenza di qualsiasi cosa (ed in particolare di luogo, tempo e vuoto), al di là del cielo delle stelle fisse e si intravede la possibilità di estendere lo spazio oltre quell’ultima sfera.

    In ogni caso sorge allora la necessità di distinguere luogo, o meglio spazio, dalla materia che lo occupa o lo delimita. E Filopono nel definire lo spazio che discende dalle precedenti osservazioni, fa proprio l’operazione di separarlo da ogni considerazione relativa al suo contenuto:

“Lo spazio non è la superficie limite del corpo avvolgente… esso è un certo intervallo, misurabile in tre dimensioni, di sua natura incorporeo, diverso dal corpo in esso contenuto; è pura dimensionalità priva di qualunque corporeità; invero, per quanto riguarda la materia, spazio e vuoto sono identici” .

Ed è proprio il fatto che, quando si sposta un oggetto da un luogo, lo spazio da esso occupato viene ad essere rimpiazzato da un’altra sostanza che rende concettualmente valida l’idea di vuoto. In ogni caso gli oggetti si spostano ma lo spazio, sotto, rimane immobile e questo spazio, proprio perché inerte, non può più essere alla base della dinamica come lo era in Aristotele, tant’è vero che, come abbiamo visto, viene rimpiazzato da un abbozzo di “teoria dell’impetus”.

Per quanto riguarda il resto della teoria di Aristotele essa viene sostanzialmente accettata, anche se qua e là occorre fare degli aggiustamenti.

E’ tutto questo molto interessante anche perché avrà, come accennato, un seguito importante poiché l’aristotelismo iniziò ad esercitare un fascino enorme anche tra i cristiani particolarmente quando gli ‘scolastici’ conobbero la Metafisica di Aristotele, 600 anni dopo Filopono. Sorse allora un forte moto di ammirazione: il sistema aristotelico poteva rappresentare il complemento filosofico, ciò che la Chiesa aveva sempre cercato, al Cristianesimo stesso, un corpo di dottrine che avrebbe finalmente nobilitato culturalmente il Cristianesimo (che fino ad allora oltre alla povera ed “incolta” Bibbia, si era affidato alle pie ma parziali visioni di Platone e dei neoplatonici). Sfortunatamente in Aristotele, più che in Platone, mancava l’idea di Dio. Questo fu il motivo per cui l’aristotelismo ebbe alterne vicende durante il 1200. Intanto già nel 1169, il Concilio di Tours aveva vietato ai monaci di leggere i pericolosi testi di fisica. Tra il 1210 ed il 1215, il Concilio provinciale di Parigi vietò l’insegnamento delle dottrine aristoteliche, condannate in blocco. Quindi altre condanne: il Concilio lateranense del 1215 (con Innocenzo III) e con la riaffermazione di Onorio III e di Gregorio IX (1231), infine, qualche anno dopo, di Urbano IV. Ancora tra il 1270 ed il 1277 sia il vescovo di Parigi E. Tempier che quello di Canterbury condannarono ben 219 proposizioni tratte dall’opera di Aristotele e dagli aristotelici (essenzialmente Averroè). Da notare che anche le tesi aristoteliche di San Tommaso erano state condannate, non già da Tempier ma dalle medesime Università di Parigi ed Oxford. In generale furono i francescani ad opporsi fermamente, in un primo tempo, all’ateismo aristotelico letto invece diversamente dai domenicani. Il contrasto tra aristotelismo e Cristianesimo (insignificanza del posto di Dio, eternità del mondo con conseguente negazione della Creazione, inesistenza del libero arbitrio in un mondo dominato dal movimento delle sfere celesti, la non immortalità dell’anima, il rigido determinismo, …) fu appianato da S. Tommaso, come vedremo oltre, un frate dell’ordine dei domenicani che si definivano i cani da guardia dell’ortodossia.

E’ istruttivo riportare ciò che riuscì a dire Duhem sulle condanne dell’aristotelismo del 1277:

Se avessimo bisogno di assegnare una data alla nascita della scienza moderna, sceglieremmo senza dubbio questa data del 1277 […] Intesa come una condanna del necessitarismo greco, questa condanna porterà molti teologi ad affermare come possibili in virtù della onnipotenza di Dio cristiano posizioni scientifiche o filosofiche tradizionalmente giudicate impossibili in virtù dell’essenza delle cose. Permettendo esperienze spirituali nuove, la nozione teologica di un Dio infinitamente potente ha liberato gli spiriti dalla cornice limitata in cui il pensiero greco aveva incluso l’universo.

Come un altro francese, A. Koyré, ha osservato: sfortunatamente il nuovo campo che si apriva alla speculazione dei filosofi e dei matematici non ha interessato nessuno. Peccato che Duhem non abbia detto anche che le condanne di Bruno e Galileo erano altrettanto benvenute perché aprivano il mondo della scienza … alla Francia (avendolo ammazzato in Italia).

ALCUNI FATICOSI E FONDAMENTALI AVANZAMENTI

Mentre si disquisiva di queste cose, che se si confrontano con i livelli delle problematiche raggiunti con Archimede, Euclide, Apollonio, … mettono in imbarazzo, altri lavoravano per ricomporre un quadro di razionalità soprattutto nella matematica che era andata perduta, anche nelle sue operazioni più elementari.

La matematica, avevamo notato anche commentando gli stupendi successi alessandrini, soffriva di un problema di fondo, il non agile simbolismo. La questione del simbolismo era rimasta la stessa a Roma. A questo problema ne va aggiunto un altro che, a posteriori, capiamo molto bene: la mancanza dello zero in una chiara numerazione di posizione ed in una non scelta di base di numerazione. Tutto ciò aveva in qualche modo fermato lo sviluppo della matematica alla geometria che, comunque, non poteva avanzare ed essere sistemata senza proprio quel simbolismo. Cosa accade in questi anni di risolutivo e di interesse ?

Seguiamo un percorso che si snoda da lontano per intersecarsi con l’Europa in questi anni. Quando Giustiniano fece chiudere le scuole non cristiane, molti studiosi, come abbiamo accennato, si diressero verso Oriente. E che in Oriente vi fossero scuole avanzate di matematica ci è testimoniato dal cristiano Severo Sebokt che nel 662 ci informa che non soltanto i greci potevano vantare conoscenze scientifiche, ma anche altri popoli (con riferimento all’India) possono vantare dei calcoli fatti con 9 simboli. Ritrovamenti archeologici ci dicono che questo modo di scrittura matematica con 9 simboli è risalente almeno al 595. Si tratta di un sistema posizionale e decimale in cui ancora non figura lo zero. Ancora un ritrovamento archeologico ci dice che certamente lo zero si conosceva in India nell’anno 876 ma non si sa se il simbolo (un segno a forma di uovo) era connesso alle altre nove cifre. Altre ricostruzioni (ad esempio: Van der Waerden) parlano ancora di quella migrazione di scienziati greci verso Oriente. Da Alessandria, dove sarebbe nato, lo zero fu trasferito in India. In ogni caso un chiaro ragguaglio sull’uso dello zero nella letteratura scientifica indiana è contenuto nel Compendio di calcolo del matematico indiano Srīdhara (991 – ?). Ma debbono passare molti decenni prima che una qualche eco di ciò giunga in Spagna per vie arabe. Le prime notizie in Europa di una numerazione indù le troviamo nel Codex Virgilianus (976), scritto nella parte cristiana della Spagna. Ancora molti decenni dopo, intorno alla metà del XII secolo, compare un trattato Prologus N. Ocreati in Helceph ad Adelhardum Batensem, magistrum suum di un certo Ocreatus, un matematico o inglese o francese probabilmente allievo di Adelardo di Bath, in cui si trova l’uso dello zero combinato con quello dei numerali romani. Questa traduzione fu una delle principali fonti di Leonardo Pisano (Fibonacci), e quindi della matematica europea.

Piano piano si elaborarono simbolismi e si introdussero metodi di calcolo soprattutto attraverso l’opera degli arabi di Spagna che introdussero quel formidabile strumento che è l’algebra. Nel 1145 l’ Al-jabr wa’l muqābalak cioè l’Algebra che al-Khwārizmī (c. 780 – c. 850) scrisse a Baghdad intorno all’830 (insieme ad una Aritmetica in cui compaiono diffusamente spiegate ed utilizzate le notazioni numeriche indiane, cioè: base decimale; notazione posizionale; un simbolo diverso per ciascuna delle dieci cifre – vedi figura) è tradotta in latino da Roberto di Chester e Gherardo da Cremona con il titolo Liber algebrae et almucabola.

Si andava quindi avanti nello sviluppo della matematica con un impulso fondamentale dato dai commerci (aritmetica) e dalla navigazione (trigonometria).

        Tutti gli autori concordano nel ritenere che, a partire da un certo momento storico (tra il Quattrocento ed il Cinquecento), i portati della tecnica nei campi della meccanica e dell’architettura civile e militare fecero riconoscere nella matematica uno strumento indispensabile. Particolarmente in Italia, dove meccanica, architettura ed arte in genere avevano uno sviluppo clamoroso, si ponevano problemi di misurazioni sempre più accurate di lunghezze, angoli, aree. Occorreva calcolare i volumi, fare degli studi prospettici, di simmetrie. Si passò così dalle cose realizzate per mera intuizione alle cose progettate razionalmente con l’uso di proporzioni, simmetrie ed armonie. Fu nel Quattrocento, in Italia, che si iniziò la pubblicazione di svariate opere che facevano largo uso della matematica: opere di Brunelleschi, di Leon Battista Alberti, di Piero della Francesca (che ci fornì la ‘divina proporzione‘, la sezione aurea), di Giorgio Martini, di Luca Pacioli. Come si vede si tratta (a parte Pacioli) di architetti ed artisti di varia natura che per la prima volta ci offrono opere che nascono ampiamente studiate e progettate con l’ausilio della matematica. E’ chiaro che la ricerca era delle migliori proporzioni, dell’armonia; è quindi evidente che sullo sfondo campeggia l’immaginerei Platonismo, sia nella sua veste pitagorica che in quella eudossiana. Elemento di grande importanza è che svariati autori iniziano a pubblicare trattati di matematica scritti in modo divulgativo, molto chiaro, accessibile a molti.
        La matematica comincia anche ad entrare come insegnamento impartito nelle Università, ‘anche se non allo stesso rango di logica o dialettica (si pensi che come ‘matematico’ Galileo guadagnava dalle cinque alle dieci volte meno dei suoi colleghi filosofi che insegnavano nella stessa Università). Gli studenti cominciano a diventare curiosi ed esigenti. Prima ci si accontentava dell’esposizione degli Elementi di Euclide, ora si volevano conoscere tutte le applicazioni pratiche della matematica, si volevano apprendere cose che poi, appena terminati gli studi, sarebbero state di immediata utilità. La domanda era così grande che addirittura sorse la professione di matematico pratico (il primo manuale di matematica pratica è l’Aritmetica di Treviso del 1478 in cui compare la prima chiara spiegazione della
moltiplicazione e divisione !).
        E nel frattempo venivano pubblicate, in traduzione latina, opere di classici greci fino ad allora sconosciute. La prima edizione latina a stampa di Euclide vide la luce a Venezia nel 1482. Nella prima metà del Cinquecento vennero pubblicate da F. Maurolico, monaco siciliano, traduzioni latine di Archimede, Apollonio e Diofanto e da P. Commandino (intorno al 1560) traduzioni di Euclide, Apollonio, Pappo, Erone, Archimede ed Aristarco. Pian piano i seguaci di Archimede crebbero. Ed ecco Nicolò Tartaglia, Guidobaldo dal Monte, Giambattista Benedetti, Giambattista Della Porta, Gerolamo Cardano. Sono tutti grandi matematici che porteranno l’algebra, la geometria e l’aritmetica a risultati del tutto insospettabili solo qualche decennio prima e nel periodo più fulgido dei matematici greci. Si realizzò anche una svolta decisiva che vide l’algebra prendere il primato sulla geometria a seguito proprio dei suoi più recenti successi (Tartaglia ci terrà a sottolineare che le sue elaborazioni non sono tratte né da Platone né da Plotino). Ed ecco ancora Bombelli, insieme all’intera scuola dei matematici bolognesi, che riesce ad affrancare la matematica dal suo uso pratico ed a farla marciare per sue linee di sviluppo totalmente indifferenti ad ogni applicazione pratica.

LA SCOLASTICA, GLI ORDINI MENDICANTI. LE UNIVERSITA’

L’inizio del XIII secolo vede in Europa il nascere di tre fenomeni di grande interesse: da una parte la riscoperta del complesso dell’opera di Aristotele, che farà molto discutere e che molto influenzerà il pensiero della Scolastica; dall’altra la fondazione delle prime università come centri dell’eccellenza del sapere; infine l’inizio dell’attività di insegnamento di alcuni ordini religiosi, detti mendicanti.

Riguardo alla cresciuta influenza del pensiero di Aristotele, si sarà osservato che i pensatori medioevali con fatica ricostruiscono alcuni sentieri di conoscenza. Mancano alcuni strumenti di fondo, essenzialmente matematici, manca soprattutto una visione complessiva dei problemi. Più in generale non sembra vi siano persone in grado di prendere in mano un Aristotele o un Platone e di sottoporli a critica serrata. Piuttosto, di fronte alle loro opere che sembravano esaustive, ci si chiedeva se l’insieme di quelle concezioni fossero coerenti ma anche cosa volessero dire alcune affermazioni. Ogni cosa non la si studiava di per sé ma in relazione alla verità di cui erano portatori i classici, come la Fisica di Aristotele, considerata vera e propria Bibbia della conoscenza della natura. Non si sentiva alcuna necessità di esperimenti perché tutto sembrava essere stato indagato dal Filosofo (così era chiamato Aristotele). Si lavorava invece alla ricerca di presunte verità attraverso le dispute sillogistiche che avvenivano allo stesso modo sia nella fisica che nella teologia: una concatenazioni di affermazioni logiche avrebbe portato a più vaste conoscenze. Probabilmente questo è stato il motivo per cui fu chi doveva sperimentare per mestiere, l’artigiano, e non il dotto professore, che offrì nuovi fenomeni da interpretare, fenomeni non considerati dal Filosofo.

Per quel che riguarda la nascita delle università devono essere fatte alcune osservazioni. Siamo in un momento in cui vi è un certo rilassamento del potere feudale che si accompagna all’inizio della decadenza della Chiesa e dell’Impero. La Chiesa inizia a perdere la supremazia sugli Stati dell’Occidente cristiano con Federico II che sarà il primo avversario e competitore dell’autorità del pontefice. I Guelfi ed i Ghibellini si fanno la guerra e da ciò discende una maggiore autonomia dei Comuni che tornano ad acquisire importanza rispetto alla campagna. L’aumento della produzione agricola del XII secolo, era anche dovuto alle invenzioni tecniche di cui ho discusso in un articolo precedente. In un processo virtuoso tecnica e produzione si aiutavano nella crescita fino al punto che si realizzano apparati tecnici in grado di produrre strumenti tecnici. Si va affermando cioè la tecnica che produce tecnica ed in definitiva un aumento dei beni complessivi in circolazione. Ciò crea un ceto artigiano sempre più diffuso ed una crescita della popolazione e del suo livello di benessere, con la conseguente affermazione dei primi ceti borghesi ricchi ed in grado di pagare persone per fare cultura. La nascita degli ordini domenicano e francescano che operano nelle città, con l’obsolescenza del benedettino legato alla campagna (ecco, appunto, perché Jaki non è andato ad evangelizzare i contadini ?), ma anche l’estendersi dei movimenti ereticali con le loro feroci repressioni, sono anch’esse conseguenza di questo cambiamento del centro di gravità delle popolazioni.

Le università che proprio in questo periodo nascono sono un chiaro portato delle migliorate condizioni economiche generali ma anche delle particolari corporazioni che le richiedono per ottenere qualche privilegio. Infatti le prime università segnano proprio i campi di interesse delle varie zone in cui vengono create: la laica e democratica Bologna sviluppa studi giuridici ed una medicina pratica; a Montpellier, zona di influenza arabo ebraica, si sviluppa una medicina teorica, ad Oxford, dove i maestri sono francescani, gli studi avranno un’impronta platonico-matematica ed agostiniana mentre a Parigi i domenicani aristotelici e naturalisti si impegneranno in teologia. Ma qualunque sia l’indirizzo di studi la costante sarà sempre del rapporto tra il sapere dell’uomo e la rivelazione cristiana con la conseguenza che, l’affinarsi di tali discorsi, porterà a sempre maggiori difficoltà per la Chiesa.

TOMMASO D’AQUINO

Tommaso d’Aquino (1225-1274) è una personalità che, pur non dando alcun contributo alla conoscenza scientifica, anzi!, è importante prendere in considerazione perché sarà il riferimento fondamentale della Chiesa, mai venuto meno fino ad oggi. E non è che io mi occupi di teologia, è che queste posizioni saranno alla base non già di una sana contestazione delle idee scientifiche, ma della loro repressione violenta (osservo solo che tratto Tommaso come chiunque altro, con rispetto. Sono gli Jaki che avvelenano i pozzi ed impediscono ogni dialogo).

Discepolo di Alberto Magno (circa 1200 – 1280), il conte Tommaso d’Aquino completò la sua opera che consistette principalmente nell’armonizzare, rendere coerente, Aristotele, letto attraverso Averroè (Ibn Rushd), Avicenna (al-Fārābī), Maimonide ed Avempace (Ibn Bājja), anche se mai citati, con il Cristianesimo, opera alla quale contribuì anche Roberto di Lincoln o Grossatesta (1175-1273). Il Papa (Alessandro IV prima ed Urbano IV poi) premeva sui professori secolari perché emendassero Aristotele al fine di renderlo accettabile, ma i domenicani avevano un progetto più ambizioso, quello di eliminare le ristrettezze della visione agostiniana ed eliminare ciò che non va in Aristotele sostituendolo con qualcosa di accettabile. Tommaso rappresenta il culmine della tradizione aristotelica con l’introduzione di qualcosa che è meno nobile della terra e sta quindi ad un livello più basso, l’Inferno, e di qualcosa che è più nobile dell’etere e sta quindi ad un livello più alto, il Paradiso. Si tratta di una sintesi puramente logica che non aggiunge nulla in termini di conoscenza dell’universo. E Tommaso non fece altro che confermare la tendenza medioevale ad assimilare la filosofia della natura alla metafisica ed alla teologia e rendere lo studio del mondo circostante un puro esercizio intellettuale elaborato con la logica sillogistica. In definitiva è Dio che comprende in sé tutto l’universo che era di Aristotele ed è Dio che trasmette il moto ad esso. In altri punti dove vi era contrasto tra Aristotele e Chiesa, semplicemente si affermò che Aristotele aveva sbagliato. E Tommaso fa un bell’esercizio della sua logica sillogistica inventandosi 5 prove dell’esistenza di Dio. La prima è per noi d’interesse perché è strettamente connessa con il sistema del mondo di Aristotele.

La catena logica è la seguente:

nel mondo esiste il mutamento;
tutto ciò che si muove è mosso da altro;
se ciò che è causa del moto, a sua volta, si muove, per il punto precedente è necessario che anch’esso sia mosso da qualche altro ente;
tuttavia, non è possibile procedere all’infinito nell’identificazione delle cause del moto, perché, in tal modo, non si troverebbe mai l’origine del moto;
ma senza l’origine del moto non ci sarebbe alcun moto, il che è contraddetto dall’esperienza;
perciò è necessario inferire l’esistenza di un “primo motore”, che non sia mosso da nient’altro. Esiste quindi un “primum movens quod in nullo moveatur”. A tale moto tutti attribuiscono il nome di Dio (ente immutabile che non diviene ma è).

Il moto delle sfere celesti è generato dalle Intelligenze angeliche. I corpi sublunari sono dislocati secondo la teoria dei luoghi naturali di Aristotele.

L’organizzazione piramidale del cosmo è analogo alla verticalità dell’ordine spirituale di Dio perfetto; al gradino inferiore nella scala delle sostanze di carattere spirituale c’è l’anima umana. Più in dettaglio, per Tommaso il mondo è unitario e con esso l’intera natura. Il tutto è regolato da un Dio con i suoi angeli che sta ad un estremo mentre l’uomo e la volgare vita terrena all’altro. Lo stesso sistema del mondo era una rappresentazione di tutto ciò. Nell’alto dei cieli Dio in cima, poi gli angeli sempre più giù a seconda dei loro gradi, quindi il cielo delle stelle fino ad arrivare giù giù all’uomo, alla Terra e, sotto di essa a quanto di più orrido si potesse immaginare: specularmente a quanto accadeva nell’alto dei cieli vi era una gerarchia di angeli maledetti (i daemon, i diavoli) organizzati anche qui in gerarchie; più si scende e più si è malvagi, fino ad arrivare al Lucifero che occupa il centro della Terra (una tale descrizione è stata resa stupendamente da Dante).

Con questo artificio molte accuse di materialismo e meccanicismo che venivano mosse ad Aristotele, piano piano andarono cadendo. A partire dal 1278 la sua dottrina divenne quella ufficiale dell’ordine dei domenicani. È interessante osservare una delle questioni che Tommaso pone nella sua Summa Theologica il fatto cioè che sembra impossibile che il corpo di Gesù sia asceso al cielo in quanto: 1) non si intravedono fori nelle sfere celesti; 2) perché i corpi che sono in stato di perfezione sono immobili e quindi non era appropriato al corpo di Gesù il movimento; 3) perché al di là dell’ultima sfera non vi è spazio ed il corpo di Gesù occupa spazio.

Non sembra possibile che Cristo sia asceso al Cielo. Infatti il Filosofo (Aristotele) dice (De Coelo, Libro Il) che le cose che sono in uno stato di perfezione posseggono il loro bene senza movimento. Ma Cristo era in uno stato di perfezione… quindi egli aveva il Suo bene senza movimento. Ma l’ascendere è movimento. Pertanto non sembra appropriato che Cristo sia asceso… Inoltre al di là dei cieli non c’è spazio, come è provato nel De Coelo I. Ma ogni corpo deve occupare dello spazio. Quindi il corpo di Cristo non è asceso al di là di tutti i cieli…
Inoltre due corpi non possono occupare il medesimo spazio. Ma dal momento che non è possibile passare da un posto ad un altro senza attraversare lo spazio intermedio, non sembra che Cristo possa essere asceso oltre tutti i cieli a meno che le sfere cristalline dei cieli non si siano aperte; il che è impossibile [Summa Theologica Parte III, Quaest. XXVII – LIX].

Ma c’è di più. Ci si rende conto di come Aristotele fosse entrato nel modo di interpretare e capire il mondo naturale se solo si pensa che addirittura Dio ne risultava limitato e occorse proprio quella condanna di Tempier del 1277 per togliere di mezzo l’idea diffusa di Dio che non avrebbe mai potuto creare un vuoto o un universo infinito o una molteplicità di mondi. E la possibilità di attaccare la teoria aristotelica, compresa quella del moto, nasceva paradossalmente proprio da quelle censure ecclesiastiche.

E’ solo un esempio di come, con Tommaso, l’astronomia verrà strettamente legata alla teologia (si veda l’intera opera di Dante) e, più in generale, della trasformazione del mondo in senso teologico, non vi era infatti argomento, per quel che ci riguarda, di filosofia naturale, che non ricadesse nel regno della teologia. Secondo Tommaso, poiché non é possibile che vi siano verità contraddittorie, religione e fede debbono andare d’accordo. Egli incita quindi a studiare la scienza perché ciò serve a consolidare la formazione religiosa ed a sradicare errori e superstizioni. La scienza a cui si fa riferimento è una scienza fondamentalmente empirica perché il modo che noi abbiamo di conoscere è fondamentalmente legato ai nostri sensi, all’esperienza che loro fanno durante la nostra vita. A questo proposito leggiamo cosa si dice nel sito Forma Mentis che si è occupato del problema del rapporto ragione-fede in Tommaso:

La collaborazione tra fede e ragione è il punto centrale della filosofia di Tommaso, punto reclamato continuamente, anche di recente, sia dal Papa polacco che da quello tedesco. Tommaso e tutta la scolastica intendono provare le verità divine per via razionale. La religione impone verità di fede indiscutibili, alle quali nemmeno la ragione può appellarsi, in quanto essa non può nulla contro la verità annunciata agli uomini da Dio. Come è possibile allora conciliare le esigenze della conoscenza scientifica (considerata aristotelicamente) con i dogmi indiscutibili imposti dalla fede? L’indagine del mondo naturale, infatti, può entrare in conflitto con le verità di fede: qualora l’evidenza di un fenomeno contrasti con le Sacre Scritture, quali parti prendere? Possibile che Dio abbia creato un mondo che entri talvolta in contrasto con le sue stesse leggi? Tommaso ritiene che Dio non possa essere così malevolo da produrre il contrasto tra l’indagine naturale e la verità divina, ovvero il contrasto tra ragione e fede. Tra filosofia e teologia non vi è dunque opposizione, seppure quest’ultima sia superiore alla prima perché portatrice di verità annunciate agli uomini direttamente da Dio. Egli non ha creato l’uomo per dotarlo di una logica ingannatrice e falsa, se una verità naturale appare talvolta in contrasto con le verità di fede, questo contrasto non è dovuto a un errore di Dio, ma piuttosto a un errore umano. Di fronte ad una contraddizione evidente tra fede e ragione, l’uomo deve quindi imparare a vedere la questione in un diverso aspetto, partendo dal presupposto che l’errore è dovuto ad un insufficiente approfondimento del problema. In altri termini la natura creata da Dio non può essere in contrasto ma solamente in accordo con le verità da Egli stesso ha trasmesse agli uomini. Ogni presunta discrepanza tra le due dimensioni consiste in un errore umano. Detto questo il metodo privilegiato per indagare la realtà è rappresentato dalla ragione, la quale ha pieno diritto di indagine naturale ed ontologica, ma solo nell’ambito ed entro i confini tracciati dalle verità di fede (i dogmi).

Riguardo ad altro aspetto che era stato importante con San Benedetto, il riconoscimento della pari dignità del lavoro manuale e di quello intellettuale, Tommaso limiterà drasticamente la regola benedettina affermando che coloro che sono sacerdoti debbono essere esonerati dal lavoro manuale:

… Il lavoro manuale è indirizzato a quattro scopi: primo e principale, ad ottenere i mezzi per sostentarsi … secondo, a vincere 1’ozio, che è colpevole di molti mali … , terzo, a imbrigliare i desideri, in quanto esso mortifica il corpo … , quarto infine, a fare delle opere di misericordia.
Se uno potesse mantenersi in vita senza mangiare, non sarebbe tenuto a lavorare con le mani. Lo stesso discorso vale per coloro i quali da altre fonti hanno quanto occorre per poter vivere in modo lecito.
In quanto però il lavoro manuale ha per scopo di vincere l’ozio o di mortificare il corpo, esso di per sé non cade sotto l’obbligo del comandamento, in, quanto oltre al lavoro manuale esistono molti altri modi di mortificare il corpo o di vincere l’ozio.
Da ultimo, in quanto il lavoro ha per scopo le opere di misericordia, esso non cade sotto l’obbligo di comandamento se non, alla peggio, nel caso in cui uno sia tenuto per un qualche dovere a compiere. delle opere di misericordia e non abbia nessun altro mezzo per aiutare i poveri.
Se quindi la regola dell’ordine non contiene particolari norme sul lavoro manuale, i religiosi non sono altrimenti obbligati al lavoro manuale che i laici. [Summa Theologica]

Nonostante le aperture di Tommaso verso la scienza, questa non decollava per svariati motivi. In primo luogo egli e gli altri pensatori erano a livelli culturali lontanissimi da quelli della gente; in secondo luogo l’insegnamento medioevale era centrato quasi esclusivamente sullo studio dei classici che ispiravano timore e rispetto per la loro autorità; in terzo luogo l’illimitata venerazione di cui godeva Aristotele non permetteva passi in avanti sostanziali; infine, e questo è un aspetto molto importante, da una parte non si disponeva di una adeguata conoscenza della matematica (si conquisterà solo nel Cinquecento) e dall’altro nessuno pensava ad intersecare processi di misura con la conoscenza della natura (non è la quantità che ci permette di conoscere l’essenza delle cose, aveva affermato Aristotele). In queste condizioni la scienza non poteva essere altra cosa che una descrizione e classificazione qualitativa alla quale l’unica dimostrazione necessaria era il ragionamento (che aiuta nella classificazione) e quindi il sillogismo (si noti che per Aristotele anche una dimostrazione geometrica è una classificazione). Inoltre la stessa organizzazione oligarchica dello stato può essere vista come giusta in quanto gerarchizzata e quindi costruita ad immagine della natura (ciò faceva molto piacere ad ogni potente).

Naturalmente mentre da una parte Tommaso saccheggiava le conoscenze arabe, dall’altra scriveva la Summa contra Gentiles (1259-1264) in polemica con i mussulmani che non si convincono della verità della rivelazione. Quegli sconsiderati dovrebbero fa ricorso alla ragione umana per convincersi, ma non intendono farlo.

Da ultimo si tenga conto per quanto vedremo più oltre che Tommaso rifiutò la teoria dell’impetus. Ciò crea una contraddizione tra i beghini curiali perché se da una parte accettano quanto dice Duhem sulla scienza che nasce dai cristiani di Oxford e Cambridge dall’altra non possono tranquillamente accettare che questa scienza cristiana sia rifiutata dal loro unico filosofo, Tommaso.

LA TEORIA DELL’IMPETUS

[Avverto subito che quanto dirò fa parte di una riscoperta successiva (risalente a circa un secolo fa) e che, all’epoca di Galileo, non ebbe particolare risonanza. Dico questo al fine di mettere a tacere alcuni personaggi che, al seguito di uno storico di parte come il cattolico Duhem, tentano di squalificare Galileo con illazioni relative a sue scoperte già fatte. Naturalmente, poiché Duhem oltre che cattolico è anche uno sciovinista francese, tali scoperte che anticipano Galileo sarebbero state fatte da francesi. Ebbene, assegnati tutti i meriti alle Scuole di Oxford e Parigi (Duhem e con lui l’altro francese Koyré li assegnano alla sola Parigi mentre l’inglese Rupert Hall ad Oxford), è incontestabile che con Galileo i problemi affrontati salgono clamorosamente alla ribalta e non si può poi dimenticare che solo studi recenti hanno portato alla luce i contributi delle due Scuole suddette, segno evidente del loro scarso peso specifico negli sviluppi del pensiero scientifico del ‘600].

Scrivono Hall e Boas Hall:

In tempi moderni, finché la scienza moderna non si liberò completamente dalla giurisdizione ecclesiastica, si sosteneva comunemente che vi dovesse essere un’ultima riconciliazione delle due verità, quella della scienza e quella del cristianesimo, che sarebbe stata raggiunta ogniqualvolta gli scienziati avessero conosciuto abbastanza. Lo scienziato medievale era meno compiacente. Egli ammetteva che alcune verità religiose erano e dovevano restare incomprensibili razionalmente, come i miracoli. In un certo senso, allora, egli adottò un
doppio metro di valutazione: nei problemi verso i quali l’autorità cristiana era indifferente – tra cui venivano comprese la maggior parte delle questioni scientifiche egli seguiva i dettami della ricerca razionale; sui problemi in cui solo il cristiano poteva avere una precisa posizione, il filosofo medievale accettava quella posizione con la forza di argomentazioni unite alla fede. […] Per Oresme, ad esempio, (stando a quanto egli dice), le argomentazioni a favore della rotazione della terra erano meramente speciose. Soltanto la diretta evidenza della rivelazione salvava l’uomo da questo errore scientifico in cui la sua ragione, da sola, lo avrebbe invischiato.
Data la concezione medievale che la ragione (sfruttando l’evidenza disponibile) poteva indurre in errore, quale era la miglior difesa contro il cadere in tali errori in quelle questioni sulle quali Dio non aveva detto nulla? Questo fu il problema cruciale della filosofia medievale, e di conseguenza anche il problema cruciale della scienza medievale, che fu sempre, da un punto di vista intellettuale, una diretta derivazione della filosofia. […] Il filosofo medievale era egli stesso erede, e coinvolto dalle circostanze, in una tradizione che si occupava dell’ambito dei concetti e delle loro implicazioni, ma non della verifica fattuale: la tradizione teologica. In teologia i fatti erano certi, rivelati, chi esponeva dottrine teologiche poteva soltanto spiegare e commentare, paragonare un passo ad un altro, rimuovere contraddizioni, mettendo in evidenza la validità di una certa dottrina nella condotta quotidiana o rafforzarne un’altra con nuove citazioni. Il teologo è limitato dai dogmi della sua religione, a meno che non perda la propria fede. Non è esagerato dire che il Medio Evo studiò la scienza come se fosse teologia e la Fisica di Aristotele come se fosse la Bibbia. I migliori contributi del filosofo – come quelli del teologo – presero la forma di lunghe postille ai testi sacri: finché egli non perse la sua fede.

Questa è una ottima premessa per cercare di cogliere i contributi di alcuni pensatori del XIII e XIV secolo.

Più in dettaglio si può dire altro. La riscoperta delle opere di Aristotele mise i pensatori del XIII e poi del XIV secolo in gravi difficoltà perché occorreva prima capire di cosa si trattava e poi tentare di inserirlo nelle poche conoscenze che si avevano cercando eventuali armonizzazioni. Il problema che a noi interessa e che fu uno dei problemi principali al quale fu posta molta attenzione con estenuanti dispute fu quello del moto che in Aristotele aveva una precisa e logica sistemazione in un universo che vedeva un tutt’uno tra cosmo e fisica. Per Aristotele, in estrema sintesi, il solo moto naturale possibile sotto il Cielo della Luna era quello che portava gli oggetti nei loro luoghi naturali. Un sasso cade per ricongiungersi con la terra, le bolle salgono dall’acqua per ricongiungersi con l’aria e così via. La caduta di un oggetto, quindi, era considerata moto naturale. Ogni altro oggetto che si muovesse in altro modo sotto il Cielo della Luna lo faceva con moti chiamati violenti, con una azione su tale corpo applicata dall’esterno (non si faccia caso al linguaggio che uso, sarebbe difficile usare e capire quello usato allora). Con la fine dell’azione esterna (la potenza) finiva il moto violento ed allora in corpo iniziava a cadere in terra. Inoltre ogni moto violento doveva essere spiegato separatamente perché non vi era una causa comunemente riconosciuta. I corpi poi hanno delle velocità dipendenti dalla sostanza che attraversano che offre una resistenza al moto. Se la sostanza si mantiene la stessa la velocità del corpo rimane costante, anche in caduta (oggi si direbbe che ad una forza costante corrisponde una velocità costante). E’ quindi il mezzo che determina la velocità di un corpo. Più il mezzo si fa denso più la velocità diminuisce, più diminuisce la densità più la velocità cresce fino, attenzione, all’assenza di sostanza (il vuoto) in cui la velocità diventerebbe infinita. Cosa impossibile perché un oggetto continuerebbe a muoversi all’infinito con velocità infinita, cose abominevoli. E quindi il vuoto è impossibile. Volendo mettere in formula quanto qui sostenuto si può dire che la velocità v di un corpo in moto è direttamente proporzionale alla potenza motrice p ed inversamente proporzionale alla resistenza r del mezzo in cui il moto ha luogo e quindi si ha (il simbolo α sta per: proporzionale):

v α p/r

Quando qualcuno nel Trecento e Quattrocento si accorse che gli oggetti in caduta sembravano aumentare la loro velocità man mano che si avvicinavano al suolo, la spiegazione fu, aristotelicamente, la seguente: l’oggetto che cade ha sempre più aria su di sé che lo spinge e sempre meno aria sotto che lo ostacola e quindi … Questo modo di ragionare fu assorbito nel suo complesso e divenne il senso comune. I filosofi si esercitavano su queste cose con discussioni che tentavano di trovare eventuali vie d’uscita tutte interna alla sola discussione. E’ fondamentale notare che quelle persone vedevano il mondo come lo vedeva Galileo e come lo vediamo noi. Non sono cambiati i fenomeni è cambiato via via il modo di interpretarli. In particolare cosa era cambiato con Galileo ? Il riferimento non erano più i libri, il filosofo, ma le osservazioni degli artigiani, dei naviganti, della gente non di università o di sacrestia. I riferimenti a ciò che accade nelle fontane di Firenze, a ciò che accade nella bottega dell’architetto, ai fenomeni che si verificano su barche, nascono in modo preponderante quando i pensatori azzardano il guardare il mondo circostante con gli occhi di chi opera in esso. In questo senso l’inerzia non poteva venir fuori da quella fisica che ho accennato ma solo dalla sua completa messa in discussione. Sull’inerzia è difficile fare esperienze in un mondo reale che è fatto di attriti, di resistenze dell’aria, di corpi non perfettamente sferici, eccetera. Si può intuire solo osservando con attenzione senza un libro di riferimento ed i racconti, prima di Bruno e poi di Galileo, su navi in movimento in cui degli oggetti vengono lasciati cadere dall’albero maestro e cadono ai suoi piedi … sono alla base delle enunciazioni dell’inerzia (e della relatività del moto).

Riguardo alla disposizione degli studiosi dell’epoca a recepire queste concezioni di Aristotele, dice molto opportunamente Butterfield:

Un universo costruito sulle basi della meccanica di Aristotele aveva la porta già mezza aperta allo spirito; era un universo in cui mani invisibili dovevano essere in perenne attività, e Intelligenze sublimi dovevano far roteare i pianeti. Oppure i corpi dovevano essere dotati di anime e aspirazioni, di una «disposizione» a determinati tipi di movimento, così che la materia stessa sembrava possedere attributi spirituali.[…]

Pertanto, al più tardi dopo i primi anni del ventesimo secolo [il riferimento è a Duhem, ndr], sorse un grande e sempre crescente interesse per quella scuola di pensatori che, in un periodo così remoto come il quattordicesimo secolo, avevano sfidato la spiegazione aristotelica del moto e avanzato l’opposta teoria dell’impetus, la quale – sebbene di per se stessa imperfetta – deve essere considerata come il primo stadio nella storia della rivoluzione scientifica. Se poi si suppone che questo tipo di tesi cada in uno dei tranelli da cui è sempre necessario guardarsi, andando a tirar fuori. dal Medioevo solo qualche preannuncio delle idee moderne o qualche casuale analogia con esse, la risposta a questa obiezione ci apparirà chiara se teniamo presente quel tipo di norme che dovrebbero servire di guida allo storiografo a proposito di tali problemi. Si tratta di una diffusa dottrina che sorge a Oxford, viene tramandata e si sviluppa a Parigi in una determinata scuola di pensatori, e, sempre a Parigi, è ancora insegnata agli inizi del sedicesimo secolo.

Quanto detto è del tutto condivisibile ed aggiungo che è anche condivisibile la priorità della scuola inglese su quella francese con buona pace dello sciovinista Duhem, senza nulla togliere ai meriti di Buridano ed Oresme che, nonostante l’uso distorto che ne fa Duhem, risultano stimabili ed apprezzabili.

GIOVANNI FILOPONO

Un precursore antico della Teoria dell’impetus fu il bizantino Giovanni Filopono (490-570) che visse e divenne direttore della Scuola di Alessandria. I suoi genitori erano cristiani ma il poveretto, anch’egli cristiano, venne giudicato eretico dai suoi correligionari (per aver tentato di spiegare la Trinità con Aristotele era arrivato alla teoria Triteista, nella quale il Dio unico si articola in tre persone legate in una triade divina, arrivando a sostenere che le tre persone sono distinte ma accomunate alla Natura Divina alla stessa maniera in cui gli individui di una stessa specie ne fanno parte. Oltre a questo negò la Resurrezione dei corpi, si schierò contro le tesi del Concilio di Calcedonia tanto che lo stesso Imperatore cristiano Giustiniano, quello che chiuse la Scuola di Atene, gli intimò di andare a giustificare l’eresia. Filopono non andò e ricevette la condanna a distanza dal Capo della Chiesa, Giovanni Scolastico, che era secondo all’Imperatore).

        Debbono passare circa novecento anni dalla morte di Aristotele perché vi sia qualcuno che rimetta in discussione alcune formulazioni non di poco conto alla base del suo complesso edificio; per la prima volta un pensatore, Filopono di Cesarea (quasi contemporaneo di Damascio), muove critiche articolare e consistenti alla concezione aristotelica del mondo.

       Secondo Filopono c’è innanzi tutto da rimettere in discussione la teoria del movimento di Aristotele. Se si lancia un proiettile “è necessario che una certa potenza motrice incorporea [chiamata vis cinetica, ndr] sia ceduta al proiettile dallo strumento che lo lancia; l’aria non contribuisce affatto a tal moto, e vi contrasta ben poco…“. Questa formulazione (che precorre la “teoria dell’impetus” poi sviluppata nel XIV secolo) fa a meno del mezzo per giustificare il movimento e considera una sorta di potenza motrice che si trasferisce da ciò che provoca il moto al proiettile che lo subisce. La fine del moto avviene per consumazione progressiva di questa potenza motrice a causa, tra l’altro, del fatto che l’aria oppone al moto una resistenza (questo almeno per quanto riguarda i moti provocati, quelli che non hanno origine naturale). Ma poiché il moto è legato al luogo, è necessario considerare cos’è il luogo. E qui viene fuori il punto più delicato della discussione: si tratta essenzialmente dello scoprire una profonda contraddizione nella definizione aristotelica di luogo. Per Aristotele “luogo è il primo immobile limite del contenente“, ebbene per quello che ora ci serve occorre puntare l’attenzione su quell’immobile. Infatti la questione che, ad esempio, si pone è: qual’è il luogo di un sasso poggiato nel letto di un ruscello? Il corpo contenente è l’acqua, per cui ad un certo istante uno potrebbe pensare che è la superficie interna dell’acqua avvolgente il sasso che costituisce il luogo del sasso.

        Ma l’istante successivo “quel luogo” si è spostato facendo posto ad un “altro luogo”. La pietra non si è mossa, essa è rimasta là ma il presupposto suo luogo cambia istante per istante. E’ chiaro che bisogna riferirsi allora a quell’immobile di qualche riga più su. Il luogo della pietra non è altro infatti che il letto del fiume su cui è poggiata. E fin qui tutto torna. Ma se applichiamo la definizione aristotelica di luogo alle sfere celesti troviamo la contraddizione di cui si diceva. Certamente il luogo del mondo sublunare è delimitato dalla superficie interna della sfera della Luna ma essa ruota e quindi si muove e quindi non può delimitare un luogo.

        Aristotele aveva però ben presente questa difficoltà tanto è vero che per lui un moto rotatorio attorno ad un centro o ad un asse fisso, poiché la sfera occupa sempre lo stesso luogo, non è da considerarsi moto locale. Filopono prende invece in esame una zona particolare di una sfera in rotazione ed osserva che questa zona occupa successivamente luoghi diversi. E’ facile concludere allora che l’intera sfera pur restando, per così dire, nello stesso luogo, occupa sempre luoghi diversi (essendo dotata quindi di moto locale).

       Rimane allora il problema: qual’è il luogo del mondo sublunare? Esso non è il cielo della Luna ma non può certamente esserlo il cielo di Giove o Saturno o qualunque altro cielo perché si muovono. In particolare neanche il cielo delle stelle fisse può delimitare un qualche luogo proprio perché anch’esso non è immobile. Inoltre se ci ponessimo la domanda del qual è il luogo in cui si muove questo cielo, dovremmo ammettere di non essere in grado di rispondere poiché non sappiamo in quale luogo esso sia non essendo noi in grado di trovare alcun “primo immobile limite” di un qualche cosa che lo contenga. D’altra parte il fatto che l’ultima sfera sia dotata di moto locale implica che anche la superficie esterna di essa occupi successivamente luoghi diversi che debbono però esservi per poter, appunto, essere occupati. E’ qui evidente che comincia a traballare l’affermazione aristotelica dell’inesistenza di qualsiasi cosa (ed in particolare di luogo, tempo e vuoto), al di là del cielo delle stelle fisse e si intravede la possibilità di estendere lo spazio oltre quell’ultima sfera.

       In ogni caso sorge allora la necessità di distinguere luogo, o meglio spazio, dalla materia che lo occupa o lo delimita. E Filopono nel definire lo spazio che discende dalle precedenti osservazioni, fa proprio l’operazione di separarlo da ogni considerazione relativa al suo contenuto: “Lo spazio non è la superficie limite del corpo avvolgente… esso è un certo intervallo, misurabile in tre dimensioni, di sua natura incorporeo, diverso dal corpo in esso contenuto; è pura dimensionalità priva di qualunque corporeità; invero, per quanto riguarda la materia, spazio e vuoto sono identici“.

Altro contributo di Filopono importante per quanto vedremo tra poco, è quello relativo alla caduta dei gravi. Egli attacca l’idea aristotelica che la caduta dei gravi implichi una maggiore velocità del corpo con maggiore peso egli con una lunga ed aristotelica discussione arrivò alla conclusione che lasciando cadere corpi di diverso peso da una stessa altezza, essi arrivano al suolo insieme⁽¹⁾.

Quindi Filopono inizia ad aprire una qualche breccia nel pensiero di Aristotele e questo gli serviva per fini teologici ma Duhem inizierà da Filopono ad individuare una continuità con la scuola francese dell’impetus sbarazzandosi di ogni altro pensatore. Operazione che, come ho già detto, corrisponde alle straordinarie imprese del sovietico Popov che aveva fatto tutto. Vi è di mezzo un doppio sciovinismo, quello del cattolico che ricerca i contributi dei cristiani per poterlo modellare come gli fa comodo e, come no?, quello dei francesi. Vedremo con quale abilità di prestigiatore Duhem si sbarazza dei contributi di Oxford. A quuesta tesi di Duhem, anche un suoi estimatore, come Crombie, deve dire: Alcuni studiosi, in particolare il Duhem, vorrebbero la teoria di Filopono all’origine di certe concezioni medioevali cha a loro volta avrebbero dato origine al concetto moderno di inerzia, che costituì la base della rivoluzione verificatasi nella dinamica durante il XVII secolo. Vedremo più avanti che questa visione di una continuità assoluta può essere contestata sulla base sia dell’autentica derivazione storica sia del carattere della concezione del moto in questione.

In ogni caso quanto sostenuto da Filopono fu ripreso dai pensatori arabi a cominciare da Avicenna e poi da Averroè. Il moto diveniva argomento filosofico di disputa.

Sette secoli dopo la teoria di Filopono alla quale ho ora accennato venne ripresa dagli arabi Di Spagna a partire da Avicenna. Il problema in discussione era relativo all’aristotelico moto violento, a cosa cioè manteneva in moto un oggetto scagliato (un proietto). Ricordo che per Aristotele era l’aria che, aprendosi lungo la strada percorsa dal proietto, si richiudeva dietro di esso sospingendolo. Per Filopono invece ciò risultava inaccettabile e, se si lancia un proietto

“è necessario che una certa potenza motrice incorporea sia ceduta al proiettile dallo strumento che lo lancia; l’aria non contribuisce affatto a tal moto, e vi contrasta ben poco…“.

Quindi il moto sarebbe possibile anche nel vuoto ed anche lì, dopo un poco, la potenza corporea ceduta al proiettile sarebbe venuta meno.

Questa polemica viene ripresa da Avicenna che in proposito sostiene che la potenza che viene impartita al dato proietto è una qualità per la quale il corpo respinge ciò che gli impedisce di muoversi, una sorta di potenza prestata, una qualità trasmessa al proietto da chi lo lancia (come il calore comunicato ad un corpo o come il suono comunicato ad una campana – quest’ultima immagine è di Galileo che in gioventù abbracciò la teoria dell’impetus). Ma Avicenna modificò quanto sostenuto da Filopono affermando che quel movimento, se fosse avvenuto nel vuoto senza impedimenti, non si sarebbe esaurito come nell’aria ma sarebbe durato all’infinito. Inoltre egli tentò una valutazione quantitativa del fenomeno affermando, con il nostro linguaggio, che la velocità acquistata da un proiettile scagliato doveva risultare inversamente proporzionale al suo peso e che se si ha a che fare con corpi in moto con la stessa velocità, essi percorrono distanze direttamente proporzionali al loro peso. Avempace, invece si mostrò d’accordo con Filopono affermando che la velocità acquisita da un corpo scagliato deve essere uguale alla potenza che gli viene ceduta alla quale deve essere sottratta la resistenza dell’aria. E ciò deve avvenire anche nel vuoto senza variazioni di velocità del corpo, dove tale corpo deve poter percorrere una data distanza come del resto mostrano le sfere celesti che si muovono con velocità finita pur essendo dotate di un moto moto senza resistenza.

Averroè attaccò queste posizioni dal suo punto di vista aristotelico. Per lui, Avempace sbaglia a trattare la natura di un corpo dotato di peso come un qualcosa di distinto dalla materia che costituisce il corpo e sbaglia a mettere in relazione le cose materiali con l’Intelligenza immateriale che muove le sfere celesti. In realtà voler parlare di impedimento al moto corrisponde a non tener conto della distinzione aristotelica del moti (naturale e violento) in quanto, se si accettasse la posizione di Avempace, tutti i moti, avvenendo attraverso mezzi corporei, dovrebbero risultare violenti.

Ho fatto questo cenno alle concezioni di questi studiosi in quanto, nell’Occidente cristiano, il punto di partenza per chi avesse voluto affrontare lo studio della Fisica e del De Coelo di Aristotele erano questi commenti ed in particolare quelli di Averroè che avevano una maggiore autorità. Ed è utile dire che questa polemica fu ripresa da Alberto Magno che si schierò decisamente con Averroè mentre Tommaso d’Aquino assunse la posizione di Avempace nel discutere di questioni metafisiche (cita tre volte questa teoria senza criticarla) ma negò l’impetus nei suoi commenti alla Fisica ed al De Coelo di Aristotele perché considerava contraddittorio un moto violento generato da un principio intrinseco. Anche qui tali posizioni avranno un grande peso negli sviluppi futuri dello studio del moto per l’enorme autorità che aveva acquistato Tommaso. Prima di andare oltre è però utile vedere un esempio dell’uso che fa Tommaso dell’impetus in questioni metafisiche. Come fa un embrione umano a venire dotato di un’anima ? La crea Dio quest’anima, aggiungendola al feto in un dato istante, o viene trasferita dal seme del padre ? Con Dijksterhuis, così lo spiega Tommaso:

Nell’ultimo caso una forza dovrebbe essere operante nel seme come strumento, e ciò diventerebbe impossibile, secondo le concezioni peripatetiche, non appena essa si fosse staccata dall’anima paterna, la quale costituisce il suo movens. In questo contesto viene citato il projectum separatum allo scopo di fare un paragone: come questo ha ricevuto dal projiciens una virtus movens intrinseca, allo stesso modo la virtus in semine patris può anch’essa essere una forza intrinseca permanente. Le opere di Tommaso d’Aquino contengono soltanto riferimenti casuali di questo genere; il problema del projectum separatum in quanto tale non viene mai sollevato.

Beh, credo si sia capito che il livello delle argomentazioni è questo.

Usciamo invece dalle discussioni estenuanti eminentemente teoriche ed occupiamoci di una questione di rilievo nella fisica di Aristotele che interessò molto gli ambienti universitari, in particolare Oxford e Parigi: il luogo, il moto e le variazioni.

Se però si vuole fare i pignoli sulle priorità vere o presunte, perché saltare da Filopono a Buridano ed Oresme ? Occorre essere coerenti e ricordare l’opera di un tedesco, Giordano Nemorario (? – 1235) che visse all’epoca dell’altro grande, Fibonacci (questo italiano ma elegantemente lo tralascio per rispetto alla memoria di Duhem). Non mi soffermo su Nemorario ma alcuni suoi contributi, che vanno nella medesima direzione di ciò che faranno ad Oxford (gestita in gran maggioranza da francescani, più legati al platonismo agostiniano) e Parigi (feudo domenicano più legati all’aristotelismo), vanno ricordati.

GIORDANO NEMORARIO

Nemorario è originario di Warburg, città della Sassonia (Sacro Romano Impero) e qualcuno sostiene si tratti di Giordano di Sassonia, che fu generale dei domenicani nel 1222. Il fatto che fosse sassone confermerebbe il nome Nemorarius, cioè straniero, ma altri lo situano a Nemi, vicino Roma. Tutto ciò vuol dire che sappiamo molto poco di lui e che ci sono arrivate varie opere con il suo nome ma non sappiamo, ad esempio, se si tratti di medesima persona. Una di queste opere, che occorre dire è la prima originale in latino, è l’Algoritmus de ratione ponderis (Libro sulla teoria del peso) in cui discute le proprietà del piano inclinato con questioni di statica, di scienza delle costruzioni, di resistenza dei materiali. Vi sono poi gli Elementa demonstrationem ponderum che in qualche modo completano le sue elaborazioni meccaniche e ci fanno intendere come queste ricerche fossero legate alla nuova architettura gotica che prendeva piede in Europa. Egli pone alla base della statica alcuni principi che sono: omnis ponderosi motum ad medium (centro terrestre) esse; Quanto gravius tanto velocius descendere; Tertia, gravius esse in descendendo, quanto eiusdem motus ad medium est rectior; Quarta, secundum situm gravius esse, quanto in eodem situ minus obliquus est descensus; Quinta, obliquiorem autem descensum minus capere de directo in eadem quantitate. Le ultime due proposizioni sono importantissime, poiché in esse è introdotto e determinato il concetto della gravitas secundum situm; cioè, come oggi si direbbe, della componente del peso nella direzione della traiettoria descritta dal mobile. Naturalmente tanto più la posizione del corpo si avvicina alla verticale (tanto minore è l’obliquità, come dice Giordano) tanto maggiore è la gravitas secundum situm, la detta componente del peso (utilizzando la trigonometria ed indicando: con F la forza, P il peso ed α l’angolo di inclinazione, la relazione si scriverebbe: F = P.senα). Così se si considera una sfera posta una volta su di un piano inclinato più prossimo alla verticale, ed un’altra su uno di assai minore inclinazione, si trova che la gravitas secundurn situm è maggiore sul primo.

Incidentalmente si deve notare che Giordano non sceglie affatto un esempio così ovvio. Ciò ha destato meraviglia, ma si spiega pensando all’origine dei problemi di Giordano in connessione con la nuova architettura.

Egli stabilisce poi una importante proposizione relativa al piano inclinato, proposizione che con linguaggio moderno recita: la forza capace di elevare un peso p ad un’altezza h può elevare n.p ad un’altezza h/n (tale principio, il germe di quello dei lavori virtuali, verrà sviluppato da Leonardo, Galileo, Descartes, … fino a Lagrange). Partendo da tale principio, Nemorario dimostra che due pesi si fanno

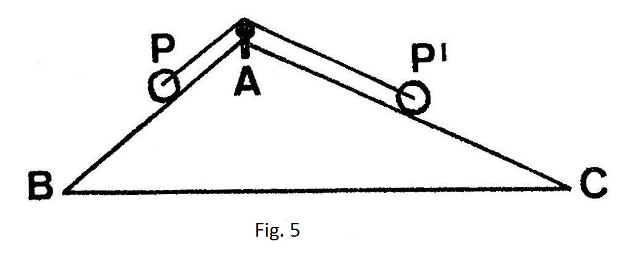
equilibrio su due piani diversamente inclinati se risultano proporzionali alle lunghezze dei piani stessi, cioè se risulta:

P : P’ = AB : AC

Oltre a questo inizio di trattazione meccanica, Nemorario scrisse anche una Arithmetica che è notevole per una novità introdotta: per la prima volta si usano lettere al posto dei numeri e la cosa permette di scrivere teoremi ed espressioni in modo generale. Nella sua altra opera, il De numeris, egli tratta del sistema numerico indo-arabo e ci fornisce per primo ed in modo del tutto generale la regola per la soluzione di un’equazione di secondo grado.

Per capire ancora meglio quali erano le questioni in discussione, all’interno delle quali discussioni ogni tanto venivano formulate argomentazioni che oggi riteniamo d’interesse, ci aiuta Alberto di Sassonia (1316-1390), uno dei pensatori operante nell’Università di Parigi, che, nel suo Questioni sugli otto libri della Fisica di Aristotele, enumera le tipiche dispute che si affrontavano con la logica aristotelica. Si tratta delle questioni alle quali i pensatori di quell’Università dovevano rispondere.

1) Se il luogo sia una superficie.

3) Se il luogo sia immobile.

5) Se il luogo naturale e proprio della terra sia nell’ acqua o all’interno della superficie concava dell’acqua.

6) Se la [superficie] concava della Luna sia il luogo naturale del fuoco.

8) Se l’esistenza del vuoto sia possibile.

9) Se un corpo semplice pesante abbia, nel suo movimento verso il basso, una resistenza interna, e similmente [se], nel suo movimento verso 1’alto, un corpo [semplice] leggero [abbia una resistenza interna].

10) Se un mezzo resistente sia richiesto in ogni movimento di corpi pesanti e leggeri.

11) Se, qualora esistesse il vuoto, un corpo pesante potrebbbe muoversi in esso.

12) Se qualcosa possa essere mosso nel vuoto, ammesso che esista, con velocità, moto locale o moto di alterazione finiti.

13) Se siano possibili la condensazione e la rarefazione.

E Grant ci informa delle modalità (perché c’erano anche quelle) di discussione delle questioni proposte:

Nelle loro risposte a tali questioni i commentatori scolastici aderirono ad una procedura formale che si era evoluta a partire dalle dispute orali tenute nelle università. L’enunciazione della questione era sempre seguita da una o più soluzioni a sostegno della tesi affermativa o di quella negativa. Se la tesi affermativa veniva considerata con favore all’inizio, il lettore poteva stare certo che 1’autore avrebbe adottato alla fine quella negativa; oppure, al contrario, se la parte negativa appariva per prima, si poteva assumere che l’autore avrebbe successivamente adottato e difeso la parte affermativa. Queste opinioni iniziali, che alla fine venivano refutate, erano chiamate «argomentazioni principali» (rationes principales). L’autore poteva poi descrivere il suo modo di procedere e magari chiarire c precisare ulteriormente la questione, o definire e spiegare alcuni termini particolari che vi occorrevano. A questo punto egli era pronto per presentare le proprie opinioni, normalmente mediante una o più elaborate conclusioni o proposizioni. Talora, per anticipare obiezioni, l’autore poteva sollevare dubbi contro le proprie conclusioni e poi risolverli. Alla fine rispondeva a ciascuna delle «argomentazioni principali», concludendo così la questione con la refutazione formale dei punti di vista opposti. Per quanto sia vero che la maggioranza di queste questiones dimostrasse scarsa immaginazione e ripetitività, è più importante sottolineare che molti degli autori scolastici più eminenti (come per esempio Guglielmo di Ockham, Giovannni Buridano, Nicola Oresme, Alberto di Sassonia e altri) trovarono in questo austero genere letterario un mezzo adeguato per interpretare Aristotele e per dare inizio ad alcune delle principali prese di distanza dalla sua fisica e cosmologia.

Dopo queste premesse, senza le quali chi non si occupa di queste complesse questioni, che richiedono conoscenze abbastanza approfondite e non una chiacchierata alla Jaki, è possibile capire gli sforzi, destinati all’insuccesso, di eminenti pensatori come Buridano ed Oresme. Ma, come ci indicano i massimi storici di queste problematiche (Hall, Boas Hall, Butterfield, Clagett, Dijksterhuis, Kearney, Boyer, …), occorre partire dall’Università di Oxford, anche se la cosa non richiede troppo spazio e tempo.

Qui e solo dopo a Parigi si iniziò a porre una questione ancora legata al moto. Abbiamo più volte visto che uno dei problemi che in senso lato la scienza aveva era la possibilità di essere rappresentata con relazioni sintetiche. E’ certamente possibile dire a parole cosa c’è dietro una formula od un grafico ma da un certo punto in poi diventa un’impresa improba con un grave rischio che dalle parole si possano intendere cose di volta in volta diverse a seconda di chi ascolta. Mentre molti studiosi elaboravano matematiche diverse (aritmetica, algebra, trigonometria, …) qualcuno iniziò a pensare alla possibilità di mettere in un disegno delle relazioni tra le grandezze che erano nelle discussioni che si facevano. Il tipo di sollecitazione veniva da un particolare moto non uniforme (che oggi chiamiamo accelerato) in cui si cercava di descrivere una grandezza che in prima approssimazione era considerata variabile in modo continuo (si ricordi quella questione riguardante un corpo in caduta che aumentava la sua velocità via via che si avvicinava al suolo).

Discussioni su questo problema furono iniziate al Merton College di Oxford verso la metà del XIV secolo da pensatori come Thomas Bradwardine (1290-1349), Richard Swineshead (? – 1354), William Heytesbury (1313-1373) e John Dumbleton (? – 1349). A questo quartetto (e particolarmente in questo caso a William Heytesbury) è dovuto il teorema della velocità media del Merton College per esprimere l’accelerazione uniforme in termini di moto uniforme. Per farlo dovettero prima passare alla comprensione della differenza esistente tra le cause del moto (che è un problema di tipo dinamico) alla sua descrizione (che è un problema di tipo cinematico). Il procedimento è descritto nel Tractatus de proportionibus (1328) di Bradwardine.

Ricordo che secondo Aristotele la velocità v di un corpo in moto è direttamente proporzionale alla potenza motrice p ed inversamente proporzionale alla resistenza r del mezzo in cui il moto ha luogo e quindi vale la relazione (il simbolo α sta per: proporzionale):

v α p/r

Già Aristotele si era posto il problema relativo ad una potenza p che non è in grado di superare la resistenza r ma la questione era restata lì. Averroè aveva tentato il superamento della difficoltà affermando che la velocità di un oggetto segue l’eccesso della potenza sulla resistenza. Questa prima affermazione venne poi sistemata da vari altri autori con l’ipotesi che si poteva avere moto solo quando si verificava la condizione:

p/r > 1

Bradwardine tentò invece un’operazione molto più ambiziosa, quella di scrivere in una formula matematica la relazione funzionale tra velocità (variabile dipendente) e potenza e resistenza (ambedue variabili indipendenti). Per far questo egli riuscì a pensare la velocità in termini di spazio e tempo ed utilizzò un teorema che era stato dimostrato da Campano di Novara nel suo commentario del V Libro di Euclide. Il teorema di Campano dimostrava che se a/b = b/c allora sarà anche a/c = [b/c]² . [Seguo ora la dimostrazione come riportata da Clagett] Bradwardine sostenne che la legge di Aristotele significava che se un rapporto dato p/r produceva una velocità v, allora il rapporto che raddoppiava questa velocità non era 2.(p/r) ma [p/r]² ed il rapporto che ne dava la metà era [p/r]^½. Utilizzando una terminologia moderna (vi prego di riflettere sulle difficoltà che si avevano a rendere semplici relazioni matematiche), la funzione esponenziale usata per mettere in relazione le variabili v, p ed r potrebbe essere la seguente v = log(p/r). E poiché log 1/1 = 0 è soddisfatta la condizione per la quale se forza e resistenza sono uguali non ne risulta alcun movimento e la formula dà un mutamento graduale continuo in v via via che p/r si approssima ad 1. E’ possibile una enunciazione più comprensibile del Teorema del Merton College: lo spazio percorso da un mobile in moto uniformemente variante è quello stesso che il mobile percorrerebbe se si muovesse con la stessa velocità pari a quella che esso ha nell’istante di mezzo. Come si può osservare la trattazione è veramente impegnativa e porta ad una importante conclusione attraverso un calcolo di tipo aritmetico, un vero tentativo di togliere i piedi dal fango delle disquisizioni. Il grave difetto, comune però a tutti i contemporanei, era che, data la relazione, non ci si preoccupò di vedere se funzionava in differenti esperienze. Il problema neppure si poneva perché le dispute venivano poste perché si rispondesse secundum imaginationem come possibilità immaginarie di analisi teorica e senza applicazione empirica (qui come a Parigi). Le dispute, come si sarà capito, erano poste per rispondere a quesiti che nascevano dalla lettura del filosofo e non come accadrà nel XVII secolo per rispondere a quesiti offerti dalla natura. Comunque il quartetto di Oxford accettò la formula, essa fu accettata da Oresme e Buridano e praticamente da tutto il mondo scientifico fino al Cinquecento (si tenga però conto che lungo la strada si susseguirono decine e decine di studi e tentativi diversi che per ovvi motivi qui non riporto).

Dopo questo minimo accenno ai chierici pensatori di Oxford, passiamo ai chierici di Parigi

BURIDANO

A temi quali luogo, moto e variazioni dette un notevole contributo uno dei maestri dell’Università di Parigi, il canonico Giovanni Buridano o Jean Buridan (c. 1300 – c. 1358) con la ripresa della teoria del moto che Filopono aveva avanzato secoli indietro e che ora diventa dell’impetus. Egli iniziò una critica dell’opera di Aristotele, sulla strada aperta da Guglielmo di Occam (c. 1295 – c. 1349), del quale dirò qualcosa più oltre, basata su osservazioni di fatti naturali non più ingenuamente empiriche ma mostrando la possibilità di intersecare l’interpretazione teorica al mero empirismo. Si tratta essenzialmente di una critica molto serrata all’idea aristotelica di movimento ma, si badi bene, tutta interna all’aristotelismo stesso come detto nell’introduzione a questo paragrafo. In realtà non si intaccano le basi profonde del filosofo greco ma si cerca al contrario di aggiornarle, di renderle più adatte ad eventuali nuove confutazioni.

Dice Buridano nel suo Quaestiones octavi libri physicorum:

La prima esperienza è quella della trottola o il torno da fabbro; questo corpo gira a lungo, eppure non esce affatto dal luogo che occupa, sicché l’aria non si sposta per riempire qualche spazio che esso lascia vuoto.
Seconda esperienza: si lanci un giavellotto che abbia all’estremità posteriore una punta acuta come quella dell’estremità anteriore. Esso si muove come un giavellotto comune, avente una sola punta; eppure l’aria che lo segue non potrebbe certo spingerlo con forza, dato che la punta posteriore tende anch’essa a tagliare l’aria.
Terza esperienza: una barca spinta rapidamente contro la corrente di un fiume, non si arresta di colpo, e continua a muoversi per un bel tratto anche quando si cessa di spingerla. Eppure chi vi sta sopra, in piedi, non si sente affatto spinto posteriormente dall’aria, anzi sente che l’aria fa resistenza al moto del suo corpo […] Con la vostra mano vuota voi potete muovere l’aria molto più velocemente che se voi teneste in mano una pietra che vi ripromettete di gettare: supponiamo dunque che quest’aria – grazie alla velocità del suo moto – abbia impeto bastante per muovere rapidamente un sasso: allora spingendo quest’aria verso di voi con la stessa velocità io dovrei darvi una spinta assai impetuosa e sensibile; ma ciò non si verifica affatto.

E prosegue spiegando in cosa consiste l’impetus:

Ogniqualvolta qualche agente mette in moto un corpo, esso gli impartisce un certo impetus, una certa potenza che è capace di muovere il corpo lungo la direzione impostagli fin dall’inizio, che sia verso l’alto, verso il basso, verso il lato o su un cerchio. Quanto più è grande la velocità che è impressa al corpo dall’agente, tanto più sarà potente l’impetus che gli sarà dato. È questo impetus che muove una pietra dopo che è stata scagliata e fino a che il moto giunge alla fine. Ma a causa della resistenza dell’aria e anche a causa della pesantezza, che inclina il moto della pietra in una direzione differente da quella in cui l’impetus è efficace, questo impetus decresce continuamente. Di conseguenza il moto della pietra rallenta senza interruzione. In definitiva, l’impetus è vinto e distrutto nel punto in cui la gravità lo domina, e da quel momento in poi quest’ultima muove la pietra verso il suo luogo naturale.[…]
Tutte le forme naturali e le disposizioni sono ricevute dalla materia in proporzione a se stessa. Di conseguenza, quanta più materia contiene un corpo, tanto più impetus è possibile impartirgli, e tanto più grande è l’intensità con cui può ricevere l’impetus. […]
Una piuma riceve un impetus così debole che è immediatamente distrutto dalla resistenza dell’aria. Allo stesso modo, se qualcuno getta proietti e mette in moto con uguali velocità un pezzo di legno e un pezzo di ferro, che hanno lo stesso volume e la stessa forma, il pezzo di ferro viaggerà più in là perché l’impetus che gli è impartito è più forte. È per la stessa ragione che è più difficile arrestare una grande ruota da fabbro che si muova rapidamente, che non una piccola. […]
L’esistenza dell’impetus sembra essere la causa per cui la caduta naturale dei corpi accelera indefinitamente. In verità, all’inizio della caduta il corpo si muove per la sola gravità. Quindi cade più lentamente. Ma ben presto questa gravità impartisce un certo impetus al corpo pesante, un impetus che è altrettanto efficace della gravità nel muovere il corpo. Quindi il moto diventa più rapido. Ma
quanto più rapido diventa, tanto più intenso diventa l’impetus. Quindi si può constatare che il moto sarà accelerato continuamente.

Come si vede le obiezioni ad Aristotele sono dense di contenuti e saranno proprio queste argomentazioni, al di là delle intenzioni di chi le muoveva e delle prime spiegazioni, ad aprire la strada al principio di inerzia (che, attenzione, qui viene negato) che, per altri versi, risulterà importante per l’affermazione di una visione relativistica del moto ed in definitiva del mondo. E’ importante osservare che Buridano applicò la teoria dell’impetus all’intero sistema aristotelico del mondo. Secondo Buridano, fu Dio che avviò il movimento delle sfere celesti, movimento che ancora va avanti grazie all’impetus. Questo associare stesse leggi ai due mondi aristotelici (quello al di sopra e quello al di sotto del cielo della Luna) comincia a rompere quella separazione aristotelica aprendo la strada ad altre rotture più importanti tra cui quella di Copernico.

Un’altra questione che Buridano prese in considerazione fu il problema del moto della Terra. Ma proprio perché non vi era alcuna nozione di moti relativi la Terra fu lasciata immobile al centro dell’universo finito.

Aristotele continuava a dominare dovunque e, come osserva giustamente Dijksterhuis, era relativamente semplice per un astronomo mettere in discussione qualche questione di carattere particolare; se il problema era solo una semplificazione dei conti, correzioni di Aristotele si potevano pure accettare, ma per il filosofo, il filosofo naturale, che doveva pensare di sostituire una immagine del mondo ad una immagine del mondo, il problema si presentava più difficile. Occorreva molto di più. Prove o indizi si dovevano accumulare ancora per secoli ma non era proprio nella mentalità dell’epoca lavorare in questo modo. La Bibbia era estremamente rassicurante per tutti.

ORESME

Ancora nello stesso periodo altri contributi d’interesse vengono elaborati dal vescovo occamista ed allievo di Buridano, Nicola Oresme o Nicole Oresme (c. 1323 – 1382). Tralasciando molte altre sue opere poco significative, sono d’interesse le sue Questioni sugli Elementi di Euclide e le De configurationibus qualitatum (opera che non fu mai stampata). Viene qui per la prima volta presentata una tecnica che pian piano rivoluzionerà i rapporti tra numeri e disegni. Egli per primo ricorse alla rappresentazione grafica per rendere evidenti le variazioni di certe qualità in funzione di alcuni parametri presi a riferimento. Per circa un secolo la Scolastica discuteva animatamente di qualità aristoteliche ora diventate forme. La variazione delle forme era argomento appassionante e per capirlo pensiamo ad una di queste forme, la velocità (ma andrebbe bene anche la temperatura). E’ evidente che, nel disquisire, si cercavano delle caratteristiche, dei modi per descrivere come variavano certe forme. Abbiamo già visto che gli strumenti matematici erano poveri ed in assenza di questi erano inevitabili lunghe ed estenuanti discussioni. Nonostante queste difficoltà ad Oxford (al Merton College tra il 1328 ed il 1350) si era riusciti a fornire a parole una legge di variazione di forme che riguarda una delle proprietà di quello che noi conosciamo come moto uniformemente accelerato (caduta di un grave), con l’accelerazione ancora non definita ma più o meno intesa come la velocità di una velocità. La legge può essere detta così (Boyer):

se un corpo si muove di moto uniformemente accelerato, la distanza percorsa sarà quella che avrebbe percorso un altro corpo dotato di moto uniforme per lo stesso intervallo di tempo con una velocità uguale a quella raggiunta dal primo corpo nell’istante di mezzo dell’intervallo temporale. Formulando tale regola con la terminologia moderna, diremmo che [in un moto uniformemente accelerato, ndr] la velocità media è la media aritmetica della velocità iniziale e di quella finale. […Siamo cioè di fronte al] valore medio di una forma “uniformemente difforme”, ossia di una forma il cui tasso di variazione è costante.

Si capisce bene che questa scoperta è quasi priva di significato se non la si formalizza per poi operare ancora su di essa. Oresme non ha gli strumenti matematici per scrivere ciò che abbiamo letto e che egli conosceva, ma mette in relazione le variazioni di intensità di una data forma (ad esempio: la velocità), distinguendo tra la sua extensio e la sua intensio. Egli introduce un sistema di due rette perpendicolari (assi coordinati), una chiamata latitudo e l’altra longitudo,

sulle quali egli riporta nell’ordine i valori dell’extensio ed intensio. Ciò vuol dire che data una forma sull’asse longitudo, la sua latitudo è il grado maggiore o minore in cui quella qualità era posseduta e le discussioni vertevano sull’intensio o la remissio di essa, se cioè essa si era accresciuta o diminuita. Si capisce che questa modo di descrivere le cose discende da quanto realizzato in ambito geografico, ad esempio da Tolomeo. Egli ha in mente di rappresentate la quantità di una forma (o anche la quantità di una qualità) per mezzo di una rappresentazione geometrica che avrebbe originato una figura. Era tale figura al centro del suo interesse perché da essa si sarebbero capite meglio le proprietà intrinseche della forma che cambiava. Come è chiaro non siamo di fronte a degli assi cartesiani, qui non c’è alcuna associazione di una figura o curva con una legge matematica che lega insieme un paio di variabili. Ma si può dire che è iniziare a porre il problema di visualizzare graficamente alcune grandezze che variano, l’una in relazione all’altra. Con il suo metodo, detto latitudo formarum perché si occupava dell’intensio et remissio formarum, Oresme dette una dimostrazione geometrica di quella legge trovata ad Oxford. Ma più che questo il dato importante è l’introduzione in matematica dello studio delle variazioni continue. Portando il tempo sulla longitudine e la velocità sulla latitudine, egli, nel suo De configurationibus qualitatum o intensionum ma anche nelle Quaestiones sugli Elementi di Euclide, lavori che furono realizzati tra il1348 ed il 1362, così ragionava:

Ogni qualità, se sarà uniformemente difforme, ha la stessa quantità che avrebbe se fosse la qualità dello stesso soggetto o di uno uguale, uniforme secondo il grado del punto medio di tale soggetto. E intendo, secondo il grado del punto se la qualità sarà lineare. Se invece sarà la qualità di una supeficie, secondo il grado della linea media …
Dimostreremo in primo luogo questa proposizione per una qualità lineare.
Sia dunque una qualità rappresentabile con un triangolo ABC. Essa è una qualità uniformemente difforme che, nel punto B, termina a zero.

Sia D il punto medio della linea rappresentante il soggetto; il grado di intensità che agisce su questo punto è rappresentato dalla linea DE. La qualità che avrà ovunque il grado così designato può dunque essere rappresentata dal quadrilatero AFGB … Ma in virtu della 26ª proposizione del I libro di Euclide, i due triangoli EFC ed EGB sono uguali. Il triangolo maggiore, che rappresenta la qualità uniformemente difforme, e il quadrilatero AFGB, che rappresenta la qualità uniforme secondo il grado de1 punto medio, sono dunque uguali. Le due qualità che possono essere rappresentate l’una dal triangolo e l’altra dal quadrilatero sono perciò anch’esse uguali, come volevasi dimostrare.
Nello stesso modo si ragiona di una qualità uniformemente difforme terminata a entrambe le estremità a un certo grado …
A proposito della velocità, si può dire esattamente la stessa cosa come per una qualità lineare, solo che invece di dire “punto medio” bisognerà dire “istante medio del tempo che misura la velocità.”
È perciò evidente che ad ogni qualità o velocità uniformemente difforme corrisponde esattamente una qualità o velocità uniforme. [citato da Crombie]

Il disegno originale di Oresme nel suo manoscritto mai stampato

Se cioè AB rappresenta l’estensione della forma (extensio formae), allora BC rappresenta la intensità variabile. La prima scoperta del calcolo fu che BC è una linea retta se questa variazione è uniforme mentre è una linea cirva se questa variazione non è uniforme. Inoltre, nel caso di variazione uniforme, l’area ABC è equivalente a quella di ABFG, quando AF = FC.

Oresme andò anche oltre poiché trovò che se la forma è la velocità, allora l’estensione verso cui è tracciata la sua intensità, deve essere il tempo e, in questo caso, come effetto si avrà la distanza percorsa. Ciò vuol dire che se la velocità aumenta da 0 a v nel tempo t, la distanza percorsa sarà ½ vt

La rappresentazione di una variazione continua mediante una figura geometrica è un notevole progresso anche se (ma non è una colpa!) mancano ancora concetti fondamentali come quelli di velocità istantanea, accelerazione, … che richiedono il concetto di limite. Una piccola notazione è d’interesse. Questo modo assai fecondo di rappresentare grandezze in grafici avrà il noto sbocco nella geometria analitica del francese Descartes mentre in Inghilterra, seguendo le orme dell’uso che, nei suoi Calculationes, fece Richard Swineshead, uno del quartetto di Oxford, delle parole fluxus e fluens, Newton svilupperà la teoria delle flussioni.

A questo punto è utile tornare a Hall e Boas Hall perché, pur non disconoscendo quanto anche Oresme fece, assegnano tutti i meriti non già all’Università di Parigi ma a quella di Oxford (i due autori sono inglesi e, pur essendo molto più laici dei francesi, non misconoscono i contributi dei loro connazionali).

Tornando a quanto anticipavo prima a proposito di ciò che interessava a Oresme (la figura e non l’andamento di una funzione), dice Boyer:

Mentre noi diciamo che il grafico della velocità di un moto uniformemente accelerato è una linea retta, Oresme scriveva: Qualsiasi qualità uniformemente difforme che termina con intensità zero viene immaginata come un triangolo rettangolo.

Non vorrei però che si restasse soddisfatti di questa acquisizione cinematica. Il fatto più importante è in realtà l’acquisizione del concetto di variabilità continua delle grandezze in matematica. E’ una assoluta novità rappresentare con una linea geometrica una variazione continua.

Ciò che ho detto è comunque tutto ciò che ebbe un qualche rilievo al chiudersi del XIV secolo. La teoria dell’impetus non ebbe maggiore trascendenza; essa nel XV secolo si diffuse a Padova, che era allora sotto il controllo non già della Chiesa ma di Venezia, e non produsse nulla di più di quanto si sapesse a Parigi. Il fatto è che le Università nate per far esplodere il meglio delle conoscenze, finite sotto gli insegnamenti di ordini religiosi o tomisti, erano diventati luoghi, lo ripeto, di inutili ed inconcludenti infinite disquisizioni.

A proposito dell’ambiente creatosi nelle Università di Parigi e di Oxford, dicono Hall e Boas Hall:

Tuttavia, questa vivacità del XIV secolo mancò il suo risultato. Le sue nuove idee e i suoi nuovi argomenti, una volta passati attraverso i secoli XV e XVI, furono un corollario della concezione del mondo di Aristotele: esse non l’avevano sostituita. E per un’ottima ragione: proprio come i filosofi medievali prestavano molta attenzione agli astratti movimenti delle sfere, senza considerare molto la reale traiettoria dei corpi celesti, e proprio come i logici medievali parlavano di empirismo e di deduzione in astratto, cosi i filosofi matematici medievali, sebbene fossero intellettualmente dotati, svilupparono un calcolo di astrazioni. Essi non affermarono che i loro teoremi cinematici si applicavano ai movimenti dei corpi reali, rendendosi magari conto che in molti casi questo non era possibile. Dedussero, correttamente, le conseguenze che dovrebbero seguire da certe supposizioni, ma non scoprirono se queste supposizioni fossero fisicamente valide o no. Cosi il Trecento indebolì di poco l’autorità delle concezioni di Aristotele su ciò che effettivamente accade in natura, un po’ più di quanto l’astronomia tolemaica avesse sminuito la cosmologia di Aristotele, come raffigurazione di ciò che sono realmente i cieli.

All’inizio del XV secolo ed oltre furono le persone dotte ed ancora gli artigiani, costituitisi come ceto borghese sempre più intraprendente, a dare importanti contributi al sorgere della scienza moderna. Serviva una nuova mentalità rispetto al mondo, non più quella statica ed immobile della rivelazione ma quella dell’imprenditore dinamico che ha bisogno di aprire i suoi orizzonti e le sue conoscenze. Nasce inoltre, nel mondo artigiano, l’esigenza di sperimentare processi produttivi, di sporcarsi le mani con prodotti artigiani sempre più raffinati che avevano dentro una quota parte sempre maggiore di scienza applicata ma ancora non formalizzata. Mentre, per parte loro, alcuni dotti⁽⁹⁾ metteranno a sempre più serrata critica le conoscenze tradizionali che dominavano ovunque. Il passo che si attendeva era quello del coniugare una matematica dotta con i processi sperimentali artigiani, un qualcosa completamente al di fuori della tradizione tomistica.

Si deve qui tener conto che nel 1447 fu inventata la stampa a caratteri mobili e che essa fu decisiva al diffondersi di conoscenze ed anche alla messa in discussione di esse: caso clamoroso fu proprio quello della Bibbia che fu letta direttamente dai cristiani ed in tempi brevi portò alla Riforma.

Osservo a margine che Clagett afferma con chiarezza che non vi è prova alcuna che Galileo abbia letto le opere manoscritte di Oresme direttamente. Si può comunque aggiungere che Galileo certamente conosceva la teoria dell’impetus perché egli la usò nella sua opera giovanile del 1590, il De Motu, quando era ancora aristotelico.

GUGLIELMO DI OCCAM

Negli stessi anni di Buridano, lavorava anche Guglielmo di Occam (1295-1349) del quale ci occupiamo, anche se brevemente, per alcune sue importanti affermazioni su questioni di relatività e di infinità dello spazio. Rispetto alla concezione di spazio o più in particolare di luogo, Guglielmo di Occam si muove nell’ambito della fisica di Aristotele, ma si può riconoscere in alcuni suoi scritti l’introduzione di alcuni elementi nuovi e degni di nota. L’adesione all’idea aristotelica di luogo è evidente dal brano seguente che richiama immediatamente il discorso di Aristotele del sasso nell’acqua.

Dice Guglielmo di Occam parlando di una nave all’ancora in un fiume:

“Benché nuove masse d’acqua salgano continuamente intorno alla nave e, quantunque la nave non occupi sempre la stessa posizione rispetto alle parti del fiume, in quanto queste si muovono costantemente, tuttavia rispetto al fiume nel suo insieme, la nave finché è ancorata giace nello stesso luogo”.

E continua:

“Se tu sei fermo, anche se tutta l’aria che ti circonda si muove, o anche se si muove un qualche corpo che ti sta intorno, tu occupi sempre lo stesso luogo; infatti sei sempre alla medesima distanza dal centro e dai poli dell’universo. Rispetto a questi punti, quindi, il luogo è detto immobile”.

        Come si vede mentre si afferma una completa adesione alle concezioni di Aristotele, si sviluppano degli argomenti che cominciano ad introdurre alla comprensione della relatività del moto; tra l’altro è interessante il fatto che viene usata la distanza rispetto al riferimento assoluto (Terra – Ultima sfera) come elemento che permette l’individuazione del luogo.

        In altra parte della sua opera Guglielmo di Occam mostrerà di rinunciare a credere che alcune determinazioni spaziali (come alto basso, centro…) abbiano un valore assoluto traendone che una possibile conseguenza di ciò potrebbe essere l’infinità del mondo (un oggetto senza un “centro” non può che essere infinito).

        Infine va sottolineato il fatto che con il nostro per la prima volta fu messa in discussione la teoria che voleva il cielo sublunare fatto di una sostanza diversa rispetto a tutti gli altri cieli.

PRINCIPALI CORRENTI DI PENSIERO DURANTE L’UMANESIMO ED IL RINASCIMENTO

        Abbiamo già intravisto due poderose correnti di pensiero che, con alterne vicende, andavano facendosi strada durante il periodo dell’Umanesimo ed il Rinascimento: il Platonismo e l’Aristotelismo. Occorre ora osservare che parlare di queste due correnti di pensiero non vuol dire necessariamente riferirsi agli autori originali. Con i tempi totalmente cambiati anche le strutture di pensiero cambiano radicalmente. Occorre aggiungere che la scoperte dei lavori di Archimede si inseriva come un cuneo o, meglio, come un’oasi di libero pensiero nella morsa Platone-Aristotele che, tra l’altro, implicava concezioni metafisiche che, a volte, potevano essere pensate non condivisibili e che, sempre, andavano a sostegno del potere costituito.
        Ebbene manca qui una corrente di pensiero originale che va affermandosi in Italia nel Cinquecento; si tratta della filosofia della natura i cui maggiori esponènti furono: Giordano Bruno, Bernardino Telesio, Francesco Patrizi, Tommaso Campanella. Grande rispetto e venerazione per tutti i classici e ripulsa non tanto verso Aristotele quanto verso il dogmatismo degli aristotelici, quanto verso il loro rappresentare la conservazione, lo status quo, il mantenimento dei privilegi.
        Questi grandi maestri sono certamente dei simboli del libero sapere in libero stato. Rappresentano l’ideale traslato al Comune di ciò che era la Polis greca. Rappresentano un’ideale di emancipazione, di giustizia e di stato moderno. Questi classici son sempre presenti, servono da stimolo ma, come sosterrà Marsilio Ficino (fondatore dell’Accademia Platonica di Firenze), quell’imitare è un creare, è un ritrovare alle fonti la complessa natura. Ma ciò che in fondo colpiva era il fatto che lo stato giusto è lo stato razionale, la possibilità di raggiungere il vivere in pace attraverso un ordine che sia in grado, in sé, di superare tutte le divergenze.
        Eppure la nuova scienza e tutto ciò che le dà vero alimento non trae la sua spinta principale dalla riscoperta di testi antichi o dalle, reazione antiaristotelica. Per convincersi di ciò basti solo pensare che il rinnovamento della fisiologia avviene proprio in ambienti aristotelici là dove si innesta la novità della sperimentazione. Insomma, come ormai concordano quasi tutti gli autori, il Rinascimento è possibile più per la miriade di artigiani, medici, architetti, costruttori, inventori che si sono succeduti negli ultimi tre o quattro secoli che non dalla pur importante riscoperta dei classici. Certo che occorre fare i conti con l’acido ed assolutamente interessato giudizio sciovinista di Koyré che afferma: L’ideale di civiltà dell’epoca che giustamente si chiama Rinascimento delle lettere e delle arti, non è in nessun modo un ideale di scienza, ma un ideale di retorica.
        Certo è che se ancora ci riferiamo ai filosofi della natura c’è almeno un elemento che li separa da quella che nel secolo successivo diventerà scienza, il fatto che anche il soggetto, l’individuo, ha una parte di rilievo nella conoscenza del mondo esterno. In questo i filosofi della natura sono tutti più vicini a Platone ma non tutti sono platonici. Essi sono tesi di più verso il mondo dei presocratici, degli antichi filosofi ionici (alla fine del secolo XV, comunque, il Platonismo cominciò a crescere, ad esempio, a Firenze dove si imponeva anche per motivi ‘nazionalisti’, poiché in fondo l’aristotelismo veniva importato da Oxford e da Parigi). Portano con loro delle forti componenti ermetiche e legate al corpuscolarismo democriteo e l’influenza sempre crescente di quest’ultimo ebbe il grande merito di separare sempre di più gli ambiti della scienza da quelli della magia.
        Ma dicevamo della rinascite del Platonismo sul finire del Quattocento. Da un lato l’Aristotelismo si era arroccato in due zone specifiche di stretta conservazione e competenza: la logica e la filosofia della natura. Ciò propiziò una coesistenza col pensiero platonico che nel frattempo si era arricchito di nuovi testi (i Dialoghi) e che rivendicava per sé l’ambito della metafisica e della teologia nelle mediazioni neoplatoniche. E, tanto per affermare di nuovo che vi fu rottura rispetto al portato dell’antichità classica, è utile notare che la polemica fu portata non da addetti alle discipline suddette ma da matematici, ottici, medici, architetti, …
        In definitiva due aspetti caratterizzarono la rivoluzione del Cinquecento e del Seicento: da une parte il riconoscimento della necessità di ‘sporcarsi le mani‘, di toccare la natura, magari attraverso la tecnica, di misurare, di ripetere i procedimenti che non fanno più parte di un gioco ma servono per sopravvivere, dall’altra parte, proprio questo approccio più metodico richiedeva metodi quantitativi più precisi ed affidabili, insomma serviva una matematica. Tutto questo rappresenta, visto con i nostri occhi, il bisogno di saldare le due principali tradizioni, l’aristotelica e la platonica. La difficoltà nasceva però non già dai procedimenti eventualmente scelti come approccio ai fatti naturali, ma nel fatto che dietro l’Aristotelismo od il Platonismo non vi erano né Platone né Aristotele ma la metafisica, il dogma, le guerre di religione, il mantenimento di privilegi e, in definitiva, il potere.
        Si capisce quindi che i rami della scienza che ebbero gli sviluppi più clamorosi furono proprio quelli in cui i processi di misura entrarono più massicciamente. Insomma i dati osservativi di Aristotele, di Platone e di Galileo sono gli stessi. Cambia il modo di interpretare le stesse cose. Si fa strada il modo di interpretare le cose che va al di là della spiegazione ingenua, nasce l’uomo teoretico. Ciascuno di noi vede il Sole sorgere e tramontare: ci vuole una grande fantasia per sostenere che il Sole è fermo. E la cosa non si può certamente dire attraverso un dogma che ne sostituisce un altro (così come oggi purtroppo è e, se non lo credete, provate a chiedere a gente qualunque se sa darvi una qualche prova di un qualche movimento della Terra). Figuriamoci quale può essere il potere di persuasione di un qualunque filosofò della natura rispetto al divino Aristotele ! Occorre cercare prove. E siccome è difficile sollevare i non credenti così in alto che possano vedere i pianeti ruotare intorno al Sole, occorre convincerli sulla Terra, con sensate esperienze e dimostrazioni. Con la meccanica. Ed è ciò che in sommo grado farà Galileo.
        C’è ancora un altro aspetto che merita un cenno. Il mondo cambia rapidamente. In quell’epoca la staticità del mondo classico sembra superata. Il cambiamento e l’evoluzione hanno in sé il portato della dinamica che da ora inizia a comparire sulla scena.
        Da questo momento non è più il dato osservativo in sé che gioca un ruolo importante ma è l’interpretazione non ingenua della realtà che fa nascere e crescere il nuovo mondo⁽²⁾.

PER ORA CONCLUDO QUI

Se si vanno a leggere i vari articoli provenienti da Il timone, da Cristianità, da Alleanza Cattolica, da Fatti sentire, e da tutto il circuito di Totus Tuus, si ricava la situazione seguente. Molti personaggi con qualifiche scientifiche nulle intervengono sulla questione del rapporto scienza e fede. Costoro si appigliano ad ogni possibile sofisma per sostenere tesi che alla fine sono quelle di un Dio che ha fatto tutto e che sa tutto e che mai la scienza potrà sapere tutto. L’ultima affermazione trova d’accordo tutto il mondo scientifico (a parte qualche scemo). La prima riguarda la fede e non intacca minimamente il lavoro dello scienziato. I ragionamenti di costoro, laici o in tonaca comprese quelle di cardinali o papi, vertono sul fatto che la scienza di per sé non può affrontare problemi diversi da quelli che vengono spessissimo definiti come materialisti. La frase che esemplifica quanto dico è la seguente:

“Nel XIX secolo le difficoltà sono aumentate con l’evoluzionismo di Darwin, che nel pensiero di molti scienziati aveva caratteri materialisti e doveva liquidare ogni idea religiosa. Ma l’incompatibilità tra scienza e fede deriva dal fatto che non si teneva conto delle differenze tra l’approccio scientifico e quello religioso ai fenomeni della vita e dell’uomo. In campo scientifico si ammetteva come unica forma di conoscenza quella sperimentale o basata sull’osservazione empirica: una concezione riduttiva, ispirata chiaramente a un’ideologia. Sul piano religioso invece si cercavano nella Bibbia risposte a domande estranee al messaggio religioso”. [da quanto sostiene Fiorenzo Facchini, prete-scienziato, in una intervista a Roberto Beretta, “Il Timone” n. 21, Settembre/Ottobre 2002].

Si può notare che continua l’affermazione di una Bibbia che ha il primato su ogni altra forma di conoscenza. Si porta a testimonianza di un dibattito un libro scritto da pastori nomadi ed ignoranti che, dal punto di vista scientifico è totalmente inutile e che lo è anche dal punto di vista umano e morale, trattandosi del libro più violento e pornografico che sia mai stato scritto. Si noterà anche che i riferimenti sono sempre Galileo e Darwin, ambedue arruolati tra i materialisti. Su Galileo si dicono sciocchezze continue in totale ignoranza e malafede (devo anche aggiungere che Gian Paolo ha avuto degli sciocchi ed ipocriti alla sua corte e tra questi arruolo anche i giornalisti che hanno spacciato la sua come riabilitazione di Galileo). Esemplifico una volta sola con Galileo:

Nella nota polemica con alcuni gesuiti e con il cardinal Bellarmino, Galileo sosteneva una posizione teologicamente corretta circa l’interpretazione della Bibbia, mentre aveva torto dal punto di vista scientifico, per varie ragioni. Ad esempio, Bellarmino chiedeva a Galileo di considerare la teoria copernicana come una conveniente ipotesi matematica e non come una verità inconfutabilmente dimostrata. Il torto scientifico di Galileo peggiorò quando si intestardì a considerare le maree come prova della rotazione assoluta della terra. Anche i suoi oppositori avevano ben capito che ciò era errato, e sarà Newton, più tardi, a dimostrare che le maree sono dovute per due terzi all’attrazione gravitazionale lunare e per un terzo a quella solare. [da Il Dio degli scienziati di Giancarlo Cavalleri, “Il Timone” n. 21, Settembre/Ottobre 2002].

Anche nella critica a Galileo in un punto in cui aveva errato si mostra la totale ignoranza delle cose di scienza e dell’argomento del contendere che è LIBERTA’ DI RICERCA. Inutile dire che poiché Galileo aveva fatto questo errore era giusto che fosse condannato. Veramente un modo canagliesco di ragionare. Riguardo a Darwin la polemica è in Europa più sotterranea perché ufficialmente la Chiesa, grazie a Padre Coyne (fatto fuori da questo Papa tedesco), l’ha accettata. Ma i chierici di sacrestia sono come i roditori o le temiti. Scavano tunnel aspettando il crollo di ciò che c’è sopra. Ed i subdoli attacchi continuano e continuano.

Come il professor Stanley L. Jaki ha più volte dimostrato e accuratamente documentato, Darwin era «ossessionato» dall’idea di fornire una spiegazione scientifica plausibile dell’origine delle specie che potesse interamente fare a meno dell’atto separato della creazione divina. La sua «teoria della discendenza», che soltanto in seguito fu chiamata teoria dell’evoluzione, era una lunga argomentazione a favore di una spiegazione «intramondana», ossia puramente materiale, meccanica, dell’«origine delle specie».[…]
Secondo le ricerche approfondite di Stanley Jaki, non resta dubbio alcuno sul fatto che Darwin, con la sua teoria, intendesse favorire la vittoria scientifica del materialismo. E Dio sa che non era l’unico a volerlo, nell’Ottocento. Non per caso Karl Marx e Friedrich Engels hanno salutato la teoria darwiniana come il fondamento scientifico della loro teoria. […]
Ma perché allora viene così caricata di ideologia e diviene uno “shibolet” materialista? Perché la visione del mondo alternativa è la fede nella creazione. Non è un caso che l’evoluzionismo ideologico sia stato l’orpello scientifico sia del comunismo che del nazionalsocialismo. [perle del Cardinale Christoph Schönborn, su”Avvenire“, 18/4/’07].

A parte il prezzemolo Jaki, continuo a ripetere, è mai possibile dialogare con costoro ? Oppure vi è altra fonte attendibile ? Se si dove si trova e chi è autorizzato a parlare per la fede ? Riescono a fare i prestigiatori: da un lato manca qualcosa alla teoria dell’evoluzione quindi non è credibile perché non spiega tutto, dall’altra in suo luogo invocano una Creazione che è totalmente al di fuori della ragione ed al massimo è un mistero della fede. Se servisse un’altra prova dell’inconciliabilità è proprio in questo contrapporre continuo di misteri a ragione. Ed anche sulla tragedia del Novecento che fu il Nazismo (ed anche il Fascismo), impropriamente legata al comunismo che è ben altro, ci sarebbe da discutere sulle complicità della Chiesa in Germania e sul fervido sostegno in Italia, in Spagna, in Portogallo e nei Paesi Balcanici e centroeuropei.

Altro argomento utilizzato dai cantori dell’oscurantismo è che vi sono scienziati credenti e questo mostra la non contraddizione tra scienza e fede. So bene che vi sono scienziati credenti e probabilmente ve ne furono di più in passato. Galileo, come si ricorda spesso, era un credente (anche se un pretoriano di Totus Tuus ricorda che era un convivente e che non volle mai sposare la sua donna ed altre amenità, mai ascoltate per altre persone). E, come credente, spiegò il senso della separazione tra scienza e fede e non si fermò mai nell’usare la sua ragione proprio perché anche la sua fede non era quella dei libri ma quella di Gesù che, nella Chiesa un poco paolina ed un poco crapulona, certamente non cristiana, è sparito. Stessa cosa per tutti gli scienziati credenti citati: in quanto scienziato nessuno ha smesso di esserlo perché, ad un certo punto, la fede gli diceva di fermarsi. Ed allora di cosa parliamo ? Si può avere fede, anche intensa, come fatto proprio, privato, personale e comunque in modo che non interferisca con gli altri e con il lavoro di scienziato, ed essere un ottimo utente della ragione. Oppure si tratterebbe di indagare cosa è la fede. Se è dedizione completa e disinteressata o solo consolazione per chi in qualunque modo soffra e sia solo. Ma lasciamo perdere perché dalle parti nostre la fede è un numero di persone battezzate che si impedisce si sbattezzino al fine di prendere in modo truffaldino i soldi dell’8 per mille.

Infine gli argomenti solidi, quelli di scienziati che difendono le tesi curiali. Abbiamo visto che quando ce n’è uno lo si munge fino allo sfinimento suo e nostro. E’ il caso di Jaki del quale ho detto. Devo comunque aggiungere che anche Jaki, intervistato da Luciano Benassi e Maurizio Brunetti per Cristianità (n° 239, 1995), dice che l’approccio dei cattolici ai problemi scienza e fede è del tutto deludente:

D. Da monaco benedettino e da accademico pontificio, lei gode di una posizione privilegiata per osservare l’atteggiamento del mondo cattolico nei confronti del dibattito scientifico. Qual è la situazione? In che misura l’egemonia della scienza e della tecnica condizionano il normale sviluppo del rapporto con la religione in ambito cattolico?
R. La reazione del mondo cattolico filosofico e teologico allo sviluppo scientifico moderno è stato, per la maggior parte, molto insoddisfacente e a volte molto confuso quando non addirittura controproducente. Insoddisfacente, poiché le nuove correnti della filosofia cattolica e della teologia sono troppo personalistiche. Come tali, esse insistono sulla soddisfazione personale, sulla sintesi personale, sulle prospettive personali. Questa enfasi spesso conduce in un mondo dei sogni concettuale che consiste nel credere sia possibile eliminare quella fondamentale linea di demarcazione fra i concetti quantitativi e quelli non quantitativi. Chi rimane influenzato da queste correnti risulta poi generalmente privo di quegli strumenti ontologici ed epistemologici opportuni per affrontare la scienza e la questione dei suoi limiti fondamentali. La scienza si limita allo studio quantitativo degli aspetti quantitativi dei corpi in movimento. Tutto il resto è filosofia, anzi metafisica. Trascurare questo punto genera solo confusione. Il personalismo promette l’aumento della forza interiore, ma in ultima analisi si rivela controproducente perché indebolisce il coraggio nell’affrontare la realtà, che, a meno di non dirsi hegeliani, garantisce la rigorosa irriducibilità fra le nozioni quantitative e quelle non quantitative. Questi due ambiti non sono in opposizione proprio perché rimangono sempre distinti l’uno dall’altro.

Giovanni Paolo II nel 1985 citò anche Enrico Medi come scienziato, prova del fatto che ha dei consiglieri farlocchi perché scienza ed Enrico Medi sono due cosa che fanno a pugni. Ultimamente va di moda Zichichi ma anche su di lui ho riempito pagine e non ne posso più di sentirlo citare. Posso solo dire che uno dei cavalli di battaglia di Zichichi nelle parrocchie è che Galileo era un cattolico e perché tale ha inventato il metodo scientifico ed è scienza solo quella che usa il metodo galileianio e quindi Darwin non ha fatto scienza (sciocchezze a modo di rosario per pregare). Feci una domanda a Zichichi nel 2002 in un sala per conferenze del Comune di Roma. Come mai questo gran credente di Galileo fu messo a tacere ? Come mai per 300 anni non si fece più scienza in Italia ? Come mai nel frattempo la Chiesa trionfante metteva su la Cattedra di Fisica Sacra alla Sapienza di Roma ? Zichichi non rispose e passò ad altro. Altre fonti da cui attingono ? Grant. Che, riferendosi a Duhem e Jaki dice che la scienza è nata da Buridano ed Oresme. Poi da qualcun altro tirato fuori dal cilindro ma perfettamente ignoto. Uno noto e di grandissima levatura che però ha poco spazio nelle polemiche da sacrestia perché è persona pensante, è Nicola Cabibbo che è addirittura Presidente della Pontificia Accademia delle Scienze. Ho riportato in questo articolo una intervista che egli ha recentemente rilasciato ad un giornale cattolico. Chapeau ! Altro che è invece un prete scienziato con aperture eccellenti è il citato Padre Coyne che è stato allontanato dalla Specola Vaticana da questo Papa reazionario per le sue posizioni apertissime senza preclusioni al dialogo.

Come si può vedere poca cosa se le loro migliori menti, ancora oggi come sempre, sono tagliate fuori⁽³⁾.

NOTE

(1) Riporto il brano di una pagina in cui Filopono argomenta contro la teoria di Aristotele della caduta dei gravi con diverse velocità a seconda del peso (da Clagett):

Il peso è quindi la causa efficiente del movimento verso il basso, come asserisce lo stesso Aristotele. Data perciò una distanza da percorrere, per esempio nel vuoto dove non c’è nulla che possa impedire il moto, e dato che la causa efficiente del moto differisce, i moti risultanti presenteranno inevitabilmente velocità diverse, anche nel vuoto … È chiaro allora che le differenze nel moto saranno causate dal peso naturale dei corpi, che avranno una tendenza verso il basso maggiore o minore. Infatti quello che ha una maggiore tendenza verso il basso fende meglio il mezzo. Ora, l’aria è divisa più efficacemente da un corpo più pesante. A quale altra causa dovremmo ascrivere questo fatto, che ciò che ha un peso maggiore ha anche, per natura, una maggiore tendenza verso il basso, anche se il moto non è attraverso un mezzo pieno? ..
E così, se un corpo fende meglio un mezzo in ragione della sua maggiore tendenza verso il basso, allora, anche se non c’è nulla da fendere, il corpo conserverà nondimeno la sua maggiore tendenza verso il basso … E se i corpi possiedono in se stessi una tendenza verso il basso maggiore o minore, possiederanno chiaramente questa differenza in se stessi anche se si muovono nel vuoto. Lo stesso spazio sarà percorso conseguentemente dal corpo piti pesante in un tempo minore e dal corpo più leggero in un tempo maggiore, anche se lo spazio fosse vuoto. Il risultato sarà dovuto non al maggiore o minore impedimento che il corpo dovrà superare nel suo moto ma alla maggiore o minore tendenza verso il basso, in proporzione al peso naturale dei corpi in questione …
Se infatti un corpo percorre la distanza di uno stadio nell’aria, e non si trova all’inizio e alla fine dello stadio in un unico istante, affinché esso percorra tale distanza dal principio alla fine sarà necessario un tempo ben definito, dipendente dalla natura particolare del corPo in questione (poiché, come ho detto, il corpo non si trova a entrambe le estremità nello stesso istante), e ciò sarebbe vero anche se lo spazio percorso fosse vuoto. Ma un certo tempo addizionale è richiesto a causa dell’impedimento del mezzo, poiché la pressione del mezzo e la necessità di fenderlo rendono più difficile i1 moto attraverso di esso.
Di conseguenza, quanto più rara supponiamo che sia l’aria attraverso cui un moto ha luogo, tanto minore sarà il tempo addizionale consumato nel dividere l’aria …
Se un sasso percorre la distanza di uno stadio nel vuoto, ci sarà necessariamente un tempo, diciamo un’ora, che il corpo impiegherà a percorrere tale distanza. Ma se supponiamo che questa distanza di uno stadio sia riempita d’acqua, il movimento non potrà più esser compiuto in un’ora, ma sarà necessario un certo tempo addizionale a causa della resistenza del mezzo. Supponiamo che per dividere l’acqua sia necessaria un’altra ora, cosicché lo stesso peso copre la distanza nel vuoto in un’ora e nell’acqua in due. Ora, se rarefacciamo l’acqua mutandola in aria, e se l’aria ha una densità pari a metà di quella dell’acqua, il tempo che il corpo ha impiegato a dividere l’acqua sarà ridotto in proporzione. Se nel caso dell’acqua il tempo addizionale era un’ora, il corpo percorrerà la stessa distanza nell’aria in un’ora e mezza. Se, ancora una volta, rendiamo l’aria densa la metà, il movimento verrà compiuto in un’ora e un quarto. E se continuiamo indefinitamente a rarefare il mezzo, si diminuirà indefinitamente il tempo richiesto per la divisione del mezzo, per esempio l’ora addizionale richiesta nel caso dell’acqua, ma non si eliminerà mai completamente questo tempo addizionale, poiché il tempo è indefinitamente divisibile.

(2) E’ utile riportare anche le opinioni di uno storico e filosofo eccellente come Eugenio Garin ed è utile tenere presente ciò quando parlerò delle sciocchezze di Padre Wallace sul preteso Plagio di Galileo su gesuiti del Collegio Romano:

La filosofia, che nel Quattrocento si era rifugiata fra politici e moralisti, chiede asilo, ora, a fisici e matematici, o addirittura agli «eretici», sbanditi da tutte le scuole. Con profondità Keplero, negli scritti famosi sul Sidereus Nuncius, riporta Galileo, non ai professori delle Università, ma a Cusano, a Copernico, a Bruno, oltre che agli antichi greci. Se legami si debbono cercare, è nella direzione di una filosofia non scolastica che conviene muoversi: la filosofia della natura di Telesio, o di Campanella, l’inquieta curiosità di Cardano e di Della Porta. In realtà i nomi che conviene fare a proposito di Galileo non sono molti, e tutti sono chiaramente indicati da lui: tra gli antichi, il suo vero maestro, il divino Archimede; tra i moderni, il «maestro nostro comune» Copernico. Interlocutori nel suo gran dialogo, Keplero come Mersenne; nello sfondo, Gilbert e Gassendi, Descartes e Hobbes. Suo avversario, non Tolomeo, ma il peripatetismo come mescolanza di fisica e teologia, dalla tradizione intrecciato ormai alla dottrina cristiana. E proprio qui si deve affrontare il problema della rivoluzione galileiana, di cosa essa fu veramente nella storia del pensiero: qui conviene dire delle vie per le quali venne affermandosi. Che Galileo conoscesse bene le discussioni dei peripatetici medievali è dimostrato dagli appunti giovanili, conservati autografi, parzialmente pubblicati dal Favaro, e da lui riferiti con buone ragioni all’84. Meno persuasiva la dipendenza di quegli appunti dai soli corsi del Buonamici: perché non da quelli del Borri e del Verino? Le ragioni derivate dal confronto col De motu non convincono, e sia il Favaro sia, in tempi molto più vicini, il Giacomelli, sembra non abbiano esaminato la cosa con attenzione. Pubblicato nel ’91, il grosso in-folio del maestro pisano reca una precisa testimonianza: l’opera è nata — egli dichiara — in seguito alle accese discussioni sul movimento che si erano avute nuper allo Studio fra scolari e maestri dei vari corsi”. L’indicazione è parallela al ricordo di Galileo, consegnato alla lettera al Mazzoni del ’97, che rinvia alle conversazioni serene ma vivaci avute col maestro cesenate, e di cui, più che eco, è documento preciso, purtroppo costantemente ignorato, una parte cospicua dell’opera maggiore del Mazzoni”. D’altra parte gli Juvenilia solo per tratti sono confrontabili col libro del Buonamici, né sembrano caratterizzati da precise corrispondenze. Comunque, lasciando impregiudicata in questa sede la questione, resta indubitata la conoscenza, da parte di Galileo, delle discussioni fisiche dei peripatetici sul moto dei gravi, sul moto violento e sul ciclo. È chiaro che di lì egli si mosse. Orbene, la grande maggioranza degli storici moderni della scienza, francesi, tedeschi, inglesi e americani, e, purtroppo, italiani, all’insegna del tema ‘i precursori di Galileo’, ha ritrovato via via, a seconda della nazionalità dello storico, nei fisici parigini, in Alberto di Sassonia e nelle discussioni da lui influenzate, nei calculatores e nei teorici inglesi de proportionibus velocitatum in motibus, pressoché tutti i motivi di Galileo, o almeno gli argomenti critici da lui usati. Al quale proposito converrebbe ricordare innanzitutto l’osservazione di Comte, ripresa dal nostro Vailati, che non si critica se non si sostituisce l’ipotesi criticata. Ora, se è innegabile che la fisica del tardo Medioevo, riprendendo argomentazioni usate dai commentatori antichi, mise in crisi non poche parti dell’aristotelismo; se è vero che i teorici dell’impeto, rifacendosi al Filopono, liquidarono la tesi del mezzo come causa del moto, è pure indiscutibile che le varie posizioni via via indicate come precorritrici di Galileo, non solo sono isolate dai loro contesti, ma mentre indicano un lavoro erosivo intorno a posizioni particolari dell’aristotelismo, non presentano proposte efficaci né per rinnovarne il metodo d’indagine, né per distruggerne i fondamenti, né per uscirne fuori in nuove teorie d’insieme. Sono singoli « pezzi » critici, destinati a rimanere sterili proprio perché non vengono abbandonati né i presupposti generali, né i procedimenti metodici. Questo è il punto da sottolineare: i meravigliosi sforzi d’ingegno dei fisici tardomedievali restano sempre prigionieri nei quadri dell’ari-stotelismo e nei suoi equivoci. Perfino gli studi del Benedetti, l’allievo del Tartaglia, usciti a Torino nel 1585, non mai citati da Galileo, ma certo a lui noti, non escono — e lo notò benissimo Vailati — dalla distruzione di singole posizioni aristoteliche, anche se, nell’allievo di Tartaglia, è rilevante l’uso di Archimede.
[…]
Noti sono gli appunti galileiani dell’ ’84, documento prezioso di una partenza aristotelica nelle questioni « del cielo», della «intensio et remissio formarum», delle qualità. In quegli autografi si riflettono esposizioni scolastiche bene informate, di ambiente pisano, come attestano, per esempio, le citazioni dei corsi di Flaminio Nobili. Che si tratti di lezioni di Francesco Buonamici, hanno ripetuto un po’ tutti, sulle orme del Favaro. Il confronto con il monumentale De motu del maestro pisano, edito a Firenze nel ’91, svela corrispondenze d’argomento molto parziali, col libro decimo, e discordanze notevoli nel tono, nelle citazioni, nel tipo di discorso. Mancano, negli Juvenilia di Galileo, i duri attacchi alle tesi dei platonici circa la corruttibilità dei cicli e l’uso della matematica. Di più: il Buonamici avverte che alla stesura del libro egli era giunto per le discussioni recenti allo Studio pisano, di uditori suoi e di colleghi, a proposito del movimento. Siamo nel ’91; del ’90 sono i più antichi scritti di Galileo sul moto, che sappiamo rispecchiare osservazioni e colloqui col Mazzoni, e che sono fortemente critici, ormai staccati dall’atmosfera circolante nell’opera coeva del Buonamici. Converrà perciò tornare sugli Juvenilia fisici; converrà leggere gli appunti, autografi anch’essi, di logica, uniti in origine agli altri, e non usati dal Favaro. Vi si affrontano questioni di rilievo, sui princìpi e l’ordine delle scienze, quali troviamo nei massimi logici del secondo Cinquecento, per esempio in Zabarella: questioni più importanti delle trite formule sulla « risoluzione » e la «composizione», ormai banalizzate, e in cui il Randall ha creduto di individuare la saldatura del metodo di Galileo col peripatetismo delle scuole. Comunque la ricomposizione di tutti gli Juvenilia gioverà anche a formarsi un’idea compiuta delle prime esperienze culturali di Galileo, e a rimetterne in discussione certi legami col Buonamici. Proprio quando questi da alla luce il De motu, Galileo si avvia per una strada diversa, destinata a portarlo fuori da quell’ordine cosmico, e da quella nozione di spazio, in cui il maestro pisano collocava con tanta fermezza i suoi corpi, gravi e lievi per natura, e per nessun’altra ragione — osservava Galileo — se non perché dovevano pur avere aliquem ordinem. La distruzione di quest’ordine, l’influenza di Archimede, la negazione di corpi gravi e lievi in sé, la trasformazione del concetto di spazio, l’inizio di quel processo che lo porterà a rifiutare un centro del mondo, e a precisare la sua concezione della relatività — tutto questo si venne legando nella mente di Galileo alla interpretazione ed accettazione del copernicanesimo come visione della realtà, non come mera ipotesi matematica.

(3) Esemplifico con il livello medio di preparazione dei pretesi interlocutori con un paio di articoli trovati sui siti che fanno capo al Vaticano frequentati e scritti da ottusi chierici detti ascari della fede. Dai soliti siti della catena Totus Tuus e satelliti vari ho ripreso (solo un paio perché la pazienza ha un limite) le istruttive riflessioni sui rapporti tra scienza e fede.

Un tal Belvecchio nell’articolo, Una riflessione sul caso Eluana Englaro, partendo dalle vicende recenti e note di Eluana Englaro, arriva al paragrafo Rapporto tra scienza e fede, dicendone di tutti i colori ed iniziando con questa frase che fa subito indietreggiare impauriti: Fuori dall’elementare riferimento di Dio, l’attività umana è velleità e illusione. In questa ottica, ogni scienza che prescinda da questo riferimento è essa stessa velleitaria e illusoria, fino a diventare suggestione e inganno, strumento della perdizione dell’uomo in cielo e della devastazione dell’uomo in terra. Chi parla non è uno stregone e neppure il mago Otelma ma un rappresentante di Inter Multiplices Una Vox, Associazione per la salvaguardia della Tradizione latino-gregoriana. Egli continua, litigando con la grammatica, affermando che impera una scienza che si pretende essere legge a sé stessa, invocando a giustificazione la indimostrabile capacità dell’uomo ad autoregolarsi (l’accento sul se che troviamo qui non è un refuso ma è ripetuto in tutto l’articolo). Ed arriva al nocciolo della sua tesi: Ciò posto, non può esistere alcun serio rapporto tra scienza e fede se non fondato sulla subordinazione della prima alla seconda. L’Una Vox pone poi il problema se la scienza non sia per caso una cosa buona visto che è anch’essa, ahimé, opera di Dio. E si risponde: se è vero che al mondo non si muove foglia che Dio non voglia, è anche vero che ogni foglia che si muove, per imprescindibile volontà divina, non per questo è un bene di per sé. E basta leggere il libro di Giobbe per rendersi conto che perfino il demonio agisce col permesso di Dio: non per questo il demonio è un bene. Questa coltissima disquisizione conclude definitivamente con: Nessuna pastorale della Chiesa di Dio dovrebbe prescindere da questa constatazione, poiché la mediazione tra scienza e fede, si traduce in una mediazione tra la verità e l’inganno, da cui può solo derivare il male dell’uomo.

Prendendo la lettura di questi brani come un impegno missionario, ci tengo a comunicare allo sventurato e paziente lettore che è durissimo farlo, una vera sofferenza. Ma stoicamente seguo.

Passo ora ad una signora che deve avere non uno ma due cilici (forse anche uno in fronte), tal Laura Boccenti (in Invernizzi, docente di Storia e Filosofia e Preside del Liceo Classico Paritario “Monforte” di Milano e collaboratrice della pagina culturale de Il Secolo, ohibò quando si dice clerico-fascismo …), che ci delizia con il suo Il cristianesimo e la scienzanello splendido sito kattolico. C’è da goderselo tutto se solo si pensa che viene introdotto nel modo seguente: Le nozioni di Creazione e di Incarnazione, presenti insieme solo nel Cristianesimo, hanno dato slancio all’impresa scientifica. Perché implicano la conoscibilità e la razionalità del mondo. Così, contrariamente a quanto molti credono, è Cristo ad avere salvato la scienza. Caspita ! La sua è una tesi forte che sono certo sarà ben argomentata. Ciò che segue però fornisce riferimenti misconosciuti nel mondo che si occupa di scienza, storia ed epistemologia. Non basta essere cattolici per dire cose giuste. Occorre studiare molto e non avere idee preconcette. Eh si, perché con i riferimenti che la filosofa fornisce non si sostengono le sue tesi: La culla della scienza moderna è stata la cristianità occidentale; solo qui essa ha potuto nascere e crescere. Questo fatto viene trascurato o negato dalla vulgata corrente che presenta la scienza come vittima della persecuzione cristiana e particolarmente della Chiesa cattolica. Secondo Stanley Jaki e Rodney Stark, l’idea che la scienza nasca dalla lotta di liberi pensatori che superano le pastoie poste della tradizione religiosa e filosofica è interamente mitologica e derivata da pregiudizi antireligiosi. Stanley Jaki e Rodney Stark chi sono costoro ? Il primo l’ho già incontrato quando diceva le solite sciocchezze cripto curiali su Galileo e Bruno. Era un benedettino, indegno di tale abito, scomparso di recente. E’ un poco il prezzemolo cattolico con qualifiche penose perché risulterebbe professore emerito della Seton Hall University, nello Stato del South Orange cioè il nulla visto che quell’università cattolica quasi non esiste (cercatela e vedrete), è più piccola di un liceo italiano. Leggendo dove ha pubblicato si trovano case editrici vaticane che non fanno testo in questioni scientifiche e case editrici di Comunione e Liberazione che, dal punto di vista della credibilità scientifica, valgono come quelle vaticane. I suoi titoli sono cioè spendibili solo in ambito cattolico, o meglio sono nell’ambito dei cattolici ignorantelli. E’ in ogni piatto perché mancano altri odori e spezie e francamente è privo di ogni credibilità. Ripete a pappagallo quanto diceva Duhem squalificando tutto il pensiero del Rinascimento e Barocco italiano. Dico questo dopo aver letto ciò che scrive che dimostra la sua completa ignoranza delle cose che racconta sia su Bruno, sia su Copernico, sia su Galileo, sia su Newton, sia su Halley. E’ più semplice dire: su tutti coloro che ha citato. Notizie più dettagliate e correzioni agli svarioni del benedettino si possono trovare qui. Rodney Stark è invece nientepopodimeno che un sociologo, caspitissima !, ed insegna in una ignota scuola l’Institute for Studies of Religion Baylor University qualcosa riguardante la religione. E’ noto perché strenuo avversario dell’evoluzione e, dico io, per questo conosciuto dai nostri clerico-fascisti che non rischiano si dica loro discendere da scimmie. Ma anche perché sostenne che Galileo, lungi dall’essere una vittima innocente degli abusi del potere, mise a rischio l’intera impresa scientifica presentando le sue teorie come certe anziché come ipotesi e deducendone conseguenze teologiche. Un vero idolo per i nostri ignorantelli con i quali c’è chi dice che uno dovrebbe confrontarsi. Ma cosa dite ? Su che ? Con chi ? Perché ? Ma quando mai ? Mi sembra di avere a che fare con D’Alema che insite a voler discutere con Berlusconi. O con Lucy che, nonostante tutte le promesse, sottrae sempre il pallone a Charlie Brown.

La nostra coltissima scrittrice dice che La scienza della natura che nasce nell’età moderna è intesa come sapere autonomo distinto dalla filosofia, come teoria controllabile attraverso l’osservazione sistematica della natura. Perché e a quali condizioni può sorgere una scienza così concepita? La domanda è posta e le risposte vengono trovate dalle aquile precedentemente citate. Stanley Jaki nel suo Cristo e la scienza (hai capito ?!) sostiene che ciò è stato possibile per la creazione e la cristologia (non ho più esclamazioni). Infatti, per la filosofia greca Dio è Logos, cioè Ragione; questa, come ha ricordato papa Benedetto XVI nella lezione di Ratisbona, è un’idea fondamentale che il cristianesimo ha assunto dalla cultura greca [allora niente radici cristiane ! ndr]. A essa corrisponde una visione della natura come ordinata e intellegibile in cui i fenomeni dipendono da relazioni causali conoscibili (le leggi della natura). Infatti il Cristianesimo non avrebbe mai potuto elaborare un concetto così complesso e poiché il mondo è ordinato allora nasce la scienza. Resta da chiedersi perché non è stata sviluppata dagli ebri nomadi nei deserti o dalla marmaglia cristiana nelle crociate. Dalle acute osservazioni precedenti segue la cosa importante: l’idea cristiana di creazione, introducendo una distinzione fondamentale tra il Creatore e la creatura, afferma la trascendenza-diversità di Dio sulla natura: l’universo è posto da un atto della sua libertà e quindi una scienza come studio di leggi necessarie non corre il rischio di avere come conseguenza anche una visione necessaria del divino. Nel cosmo cristiano non esistono corpi divini, tutti gli enti sono semplici creature. Ma la Grecia, nonostante sia stata la culla della razionalità non è la patria della scienza moderna (anche perché non è moderna). E lo Jaki che cerca Buridano ed Oresme per annullare Galileo fa un salto logico pauroso perché dimentica il tributo dovuto all’ellenismo riscoperto che permise moltissimi degli avanzamenti rinascimentali. La conclusione lascia però di stucco: Il cristianesimo, oltre a concepire Dio come Creatore, afferma anche che Cristo, Unigenito Figlio di Dio, si è incarnato nella storia. Questo fatto, liberando l’uomo da una visione ciclica e fatalistica degli avvenimenti, rende possibile l’idea di progresso. Ma qualcuno di voi, ci avrebbe mai pensato ? E non è finita: Dopo l’Incarnazione, il compito di dominare la natura e sottometterla, già consegnato a Israele, viene inteso come collaborazione, mediante il lavoro, all’attività creatrice, ordinatrice e redentrice di Dio. Con la conseguenza che, come con il gioco dell’oca si torna al chiodo fisso di Duhem: Saranno così i secoli della cristianità medioevale a segnare l’inizio del progresso scientifico e l’introduzione nella vita quotidiana delle relative innovazioni tecnologiche. Ed il tutto va a conclusione con le stesse parole di Jaki (mentre l’altro si deve essere perso per strada): Cristo ha salvato la scienza riscattandola da una sindrome «quella delle sue numerose e clamorose mancate nascite in tutte le grandi culture antiche […] fu (Cristo) all’origine della sua sola nascita vitale all’alba dei tempi moderni. I medievali furono i primi a definire se stessi moderni ed avevano ragione di farlo anche rispetto alla prospettiva scientifica, che soltanto in seguito si delineò in tutta la sua imponenza». AMEN.

Abbiamo terminato con la clerico-fascista e per me è un vero sollievo. Ma ci si rende conto dell’entropia che si genera con questo mare di sciocchezze profuse gratuitamente nell’aire ? E ci si rende conto sul cosa possono apprendere cittadini qualunque da questa montagna di parole che fanno pensare al calcolo del probabilità, alla famosa scimmia che si mette davanti alla macchina da scrivere per tentare la costruzione della Divina Commedia. E’ un’altra prova, ritenti.

BIBLIOGRAFIA

(1) M. Clagett – La scienza della meccanica nel medioevo – Feltrinelli 1972

(2) A. C. Crombie – Da S. Agostino a Galileo – Feltrinelli 1970

(3) E. J. Dijksterhuis – Il meccanicismo e l’immagine del mondo – Feltrinelli 1971

(4) Edward Grant – La scienza nel Medioevo – il Mulino 1997

(5) U. Forti – Storia della scienza – dall’Oglio 1968

(6) R. Taton (diretta da) – Storia generale delle scienze – Casini 1964

(7) A. Koyré – Studi galileiani – Einaudi 1979

(8) A. Koyré – Études d’histoire de la pnsée scientifique – Gallimard 1973

(9) H. Butterfield – Le origini della scienza moderna – il Mulino 1962

(10) A. R. Hall, M. Boas Hall – Storia della scienza – il Mulino 1979

(11) C. B. Boyer – Storia della matematica – Mondadori 1990

(12) Eugenio Garin – Scienza e vita civile nel Rinascimento – Laterza 1965

(13) Hugh F. Kearney – Science and Change. 1500-1700 – World University Library, Weidenfeld, 1970.

‹ FEDE CONTRO SCIENZA (Parte 1)

LA SCIENZA FISICA NEL TARDO MEDIOEVO: DAL SECOLO XI AL XIV ›

Categorie:SCIENZA E FEDE

Fisicamente

di Roberto Renzetti

FEDE CONTRO SCIENZA (Parte 2)

Rispondi Cancella risposta

FEDE CONTRO SCIENZA (Parte 2)

Condividi:

Rispondi Cancella risposta