Roberto Renzetti

1 – INTRODUZIONE

        Nella ricostruzione storica del periodo che va tra il Seicento ed il Settecento, in ambito scientifico, non può mancare uno studio su Leibniz. Il personaggio è certamente più noto in ambito filosofico ma anche in ambito scientifico il suo contributo, soprattutto in matematica, è stato di primissimo piano e per comprendere alcuni momenti fondamentali di questo fecondo periodo storico, occorre sforzarsi di cogliere tutti i passaggi del dibattito scientifico.

        Ho già avuto modo di dire che, dopo Galileo, il baricentro della ricerca scientifica si sposta a Nord.  Abbiamo già discusso di Descartes e di Huygens. Ora mi occuperò di Leibniz. Siamo nel Nord Europa dove proseguono proficuamente le elaborazioni iniziate in Italia (tanto che, non lo si dimentichi, la scienza parla ancora in latino). Restano ancora molte eminenti personalità che, da punti di vista diversi o concorrenti hanno permesso l’affermarsi della scienza, del pensiero razionale sull’oscurantismo, la superstizione e la magia. Dovrò occuparmi di Berkeley, di Newton, di Hooke, di Pascal, di Gassendi, di Boyle, … Sono stati passi faticosi e duri, spesso pagati a carissimo prezzo, soprattutto in Italia. Ed il fatto straordinario è che, ancora oggi e, anche qui, soprattutto in Italia, in un mondo che dovrebbe essere laico e quindi razionale, occorre battersi per l’affermazione del libero pensiero. La segreta speranza è che conoscendo un poco di storia del pensiero scientifico si facciano dei passi in avanti, siano coinvolte sempre più persone nella comprensione di cosa possono gli spiriti liberi, le persone che possono esercitare il loro pensiero senza condizionamenti in generale e metafisici in particolare.

        Per mia competenza e perché il resto del pensiero di Leibniz è ben studiato ed approfondito da tutti i punti di vista in ambito filosofico, io mi occuperò solo del Leibniz scienziato con qualche cenno alle sue posizioni generali.

2.1 – PAGINE DELLA VITA E CRONOLOGIA DELLE OPERE

        Gottfried Willhelm Leibniz nacque a Lipsia, uno dei centri culturali più importanti del Centronord Europa, nel 1646. Siamo in Sassonia e la famiglia di Leibniz, di origine slava (suo nome originario era Lubeniecz),  è alto borghese, benestante e luterana. Suo padre, Friedrich, è notaio, giurista e professore di filosofia morale all’Università e sua madre Catharina Schmuck è figlia di un noto avvocato. Il giovane Leibniz resta ben presto orfano di padre (1652) e sulle orme del padre inizia precocissimamente a muoversi sotto la guida religiosa e morale della madre che ebbe molta importanza nella sua educazione. Frequentò la scuola Nicolai di Lipsia ma, dopo la morte del padre, si formò da solo sui  libri della sua biblioteca che contenevano, oltre a testi di diritto, testi sacri (come si conveniva all’alta borghesia europea) e testi di classici greci e latini (sembra che già ad otto anni avesse una qualche conoscenza di latino  con predilezione per Tito Livio, Cicerone e Virgilio). Per suo conto studiò metafisica, teologia scolastica e la logica aristotelica (sillogismi) con particolare riguardo alla comprensione dell’ordinamento in classi dei predicati ma non delle proposizioni (che presto svilupperà in un lavoro sull’arte combinatoria).

        Nel 1661, all’età di 15 anni (non straordinaria all’epoca), lasciata la scuola Nicolai, entrò all’Università di Lipsia dove fece studi giuridici e simultaneamente studiò filosofia (Aristotele ed Euclide), retorica, il latino, il greco e l’ebraico. Ottenne il baccellierato in Filosofia e Lettere nel 1663 con la tesi Disputatio Metaphysica de Principio Individui nella quale, su cammini aperti da Avicenna, Duns Scoto e Tommaso d’Aquino, sostenne dei concetti che sono all’origine della sua teoria delle monadi (l’esistenza dell’individuo è nella sua interezza che non si può spiegare né con la sola materia né con la sola forma). Nel 1663 Leibniz frequentò a Jena i corsi di matematica ed anche di filosofia di Erhardt Weigel. E’ una tappa importante per la sua formazione perché Weigel imposta il suo corso dando risalto alla matematica che contrappone alle dispute scolastiche. Nel rivendicare la bontà del suo metodo egli invitò gli interlocutori scolastici a tradurre in tedesco le formule latine, riuscendo ad ottenere effetti comici  che provocarono il riso di tutto il pubblico. Ebbe modo di ottenere altri titoli accademici: quello di Magister philosophiae nel 1664 (discutendo una tesi, Specimen difficultatis in jure, seu quaestiones philosophiae amaeniores ex jure collectae, in cui Filosofia e Diritto erano trattati insieme mediante alcuni aspetti della matematica che aveva appreso da Weigel, con l’argomento cardine del diritto che nelle università tedesche, senza filosofia, è un labirinto senza uscita) e quello di baccelliere in diritto nel 1665 con la tesi Disputatio juridica de condicionibus. Subito dopo l’ottenimento del titolo di Magister, ebbe il dolore della scomparsa della madre. Nel 1666, come tesi per il dottorato in Diritto a Lipsia, scrisse Dissertatio de arte combinatoria in cui riprese le sue intuizioni di sei anni prima. In pratica allora si era chiesto de fosse possibile riunire in classi non solo i predicati ma anche le proposizioni ed ora in quest’opera rispondeva al quesito con la derivazione di enunciati di eventi complessi a partire dagli enunciati di eventi semplici mediante il calcolo logico combinatorio e la riduzione di ogni concetto, ragionamento, scoperta ad una combinazione di elementi base, come numeri, lettere, suoni, colori. Lo stesso Leibniz affermava che il suo era un metodo generale, grazie al quale ogni verità della ragione sia ridotta ad una specie di calcolo. Nello stesso tempo una specie di linguaggio o di scrittura universale, ma infinitamente diversa da tutto ciò che è stato fino ad oggi, perché i simboli e le parole, guiderebbero la ragione, e gli errori, salvo quelli di fatto, sarebbero semplici errori di calcolo. Sarebbe difficilissimo formare o inventare questo linguaggio, o caratteristica, ma sarebbe facilissimo comprenderlo senza alcun dizionario (in questo Leibniz crede che tutte le verità siano in noi e possano essere chiarite con un dibattito dal carattere matematico. Evidentemente egli trascura il ruolo fondamentale dell’esperienza in accordo con quanto ormai dovrebbe essere chiaro, la via aperta da Galileo è stata seguita dal solo Huygens. Ma qui, probabilmente vi è una posizione che reagisce all’empirismo dilagante dei lavori di Locke).  Leibniz, fin da giovanissimo, aveva studiato l’arte combinatoria del catalano Ramon Lull (1232-1315) ed aveva ricavato delle conclusioni che contrastavano con quelle della logica aristotelica. Si era però convinto che era egli stesso a sbagliare. In seguito, piano piano, acquistò confidenza nei suoi risultati fino ad arrivare a questa pubblicazione nella quale si anticipa di 200 anni la nascita della logica simbolica con l’introduzione dell’addizione e moltiplicazione logica, della classe nulla e quella conclusiva, della negazione e l’identità. Ma come suo costume Leibniz lasciò il lavoro senza ulteriori elaborazioni e questi suoi studi furono riscoperti nella seconda metà dell’Ottocento solo dopo che altri (De Morgan e Boole) li avevano riconquistati in modo indipendente. Si capì questa parte fondamentale del pensiero di Leibniz solo dopo i lavori di Russell, Peano, Frege, Whitehead ed Hilbert. Ma questo lavoro non dette a Leibniz il successo sperato perché non gli fece superare l’esame di dottorato (vi sono varie versioni: una afferma che per la sua giovane età, un’altra dice che le sue tesi erano eterodosse, un’altra ancora per un intervento contro Leibniz  sul decano dell’università da parte della moglie di quest’ultimo). Egli si rivolse allora all’Università di Altdorf (vicino Norimberga) dove presentò la tesi De Casibus Perplexis che gli fece ottenere il dottorato in Diritto nel febbraio 1667. Questa Università gli offrì una cattedra che egli rifiutò perché aveva altre intenzioni.

        Si trasferì a Norimberga dove aderì ad un circolo di alchimisti che lavoravano alla trasmutazione dei metalli, quasi seguendo le orme di Descartes con i Rosacroce con la differenza che i primi erano meno nascosti dei secondi. Per chiedere l’adesione ed averla in breve tempo aveva scritto una lettera piena di termini oscuri e contorti, presi da testi di vari alchimisti che neppure egli stesso capiva. Naturalmente la cosa fece impressione e si credette che il giovane Leibniz sapesse molto di quei misteri da iniziati. Fu ammesso subito con il grado di segretario e con uno stipendio non disprezzabile.

        Durante la sua permanenza a Norimberga fece amicizia (1667) con il barone di Boineburg, importante personalità alla corte di Magonza, che lo portò con sé a Francoforte. Qui Leibniz scrisse (1667), con dedica all’Elettore di Magonza, il vescovo von Schönborn, la Nova methodus discendae docendaeque jurisprudentiae opera in cui proponeva di ridurre l’intero corpo del diritto in solo nove capitoli, iniziando un cammino per l’unificazione del diritto in tutta la Germania. Nel 1668 l’Elettore lo invitò a corte per svolgere alcuni incarichi di assistente al riordino del diritto civile. Scrisse, ai fini di un viaggio diplomatico in Polonia del barone Boineburg, lo Specimen demonstrationum politicarum pro eligendo rege Polonorum. Sempre per Boineburg scrisse la Defensio Trinitatis per nova reperta logica in polemica con il polacco A. Wissowatius. Scrisse poi Confessio Naturae contra Atheistas e nel 1669 curò una nuova edizione dell’ Anti-Barbarus seu de veris principiis et de vera ratione philosophandi contra Pseudophilosophos (con una prefazione in cui tentava di conciliare l’aristotelismo con la filosofia dei moderni, ideale sempre inseguito da Leibniz), opera dell’umanista italiano Nizolio. Durante l’estate del 1669, in un viaggio con Boineburg, conobbe Erich Mauritius che gli segnalò alcuni lavori di C. Wren e C. Huygens, sugli urti dei corpi. Da quel momento iniziò ad interessarsi del problema e scrisse due lavori: Theoria motus abstracti, che inviò all’Accademia delle Scienze di Parigi, e Theoria motus concreti che inviò alla Royal Society di Londra; i due lavori furono riuniti nell’Hypothesis Physica Nova, pubblicata nel 1671 e della quale discuterò a parte.  L’Elettore, nel 1670, lo nominò giudice presso l’Alta Corte d’Appello. Ma Leibniz aveva già fatto varie conoscenze di personalità di spicco della Royal Society di Londra ed era in corrispondenza con varie di esse, tra cui il Segretario, Oldenburg, di tale Society. Nel 1671, oltre al libro già citato, Leibniz continua con le sue dispute teologiche e pubblica: De usu et necessitate demonstrationum immortalitatis animae e  De resurrectione corporum.

        Nello stesso anno, con la Francia che si riarma vistosamente, la Germania teme e prepara la guerra. Nel 1672 Leibniz è inviato a Parigi insieme ad una delegazione diplomatica per tentare di dissuadere Luigi XIV dalla guerra all’Olanda. Un progetto alternativo di Leibniz viene proposto al Re Sole: invadere l’Egitto e da lì marciare, attraverso la Turchia, verso i possedimenti coloniali olandesi delle Indie in modo da debilitare in tal modo l’Olanda. Questa idea molto acuta di Leibniz non venne presa in considerazione e si iniziò una guerra che durò 7 anni. L’esercito francese, forte di 200 mila uomini, non riuscì però a sconfiggere l’Olanda che costrinse la Francia alla pace di Nimega. Leibniz restò però a Parigi per occuparsi del figlio di Boineburg che era studente in questa città, andando ad incontrare i suoi corrispondenti dell’Accademia delle Scienze e conoscendo qui la personalità che più lo emozionò ed influenzò, Huygens (come Leibniz stesso racconta in una lettera a Bernouilli in cui descrive i suoi studi matematici) che gli fornì le prime fondamentali conoscenze in matematica avanzata.

        Alla fine del 1672 muore il suo protettore Boineburg e non avendo più un incarico per restare a Parigi, si recò a Londra (1673) con altra missione diplomatica. Qui conobbe il fior fiore degli scienziati inglesi, tra cui Wallis, Boyle e Newton, che lo accolsero con ossequio assistendo alla sua presentazione alla Royal Society di un modello in legno di una macchina calcolatrice da lui realizzata come perfezionamento di quella di Pascal (qualche mese dopo sarà nominato membro della Royal Society). In questa città ebbe la notizia della morte dell’Elettore von Schönborn che gli dava da vivere e quindi ritornò a Parigi dove ben presto si ritrovò senza mezzi di sussistenza. Chiese aiuto ad un vecchio conoscente, il duca Johann Friedrich di Brunswick-Lunebourg, che glielo concesse nominandolo consigliere, bibliotecario ed archivista con uno stipendio degno e la libertà di risiedere dove credesse meglio. Fu questo un momento di grande libertà per lui, libertà e tempo che gli permisero di dedicarsi allo studio della matematica che per lui era una completa novità, in quanto era nota solo in Italia, Francia ed Inghilterra. Sotto lo stimolo di Huygens, studiò gli scritti di Pascal (tra cui anche i Pensieri da cui trasse ispirazione per la sua Teodicea) e la Geometrie di Descartes e riuscì a cogliere tutto ciò, molto, che Descartes aveva lasciato in sospeso. Alcuni manoscritti scoperti intorno alla metà dell’Ottocento mostrano che, dalle letture di Descartes, Leibniz aveva ricavato già nel 1673 che il problema diretto ed inverso della tangente ad una curva sono tra loro strettamente relazionati e che l’ultimo è in realtà un problema di quadratura. Inoltre aveva risolto alcuni problemi proposti dallo stesso Descartes, come quello delle proprietà speciali di alcuni ovali che Descartes aveva studiato per realizzare fenomeni di riflessione e rifrazione studiati nella Dioptrique, ma la cui soluzione era stata occultata. La soluzione che trova Leibniz è in un manoscritto dal titolo Inquisitio in methodum qua Cartesius invenerit propietas suarum ovalium lib. 2 Geometr. E proprio cimentandosi con questo problema Leibniz comprende che si tratta di una quadratura che deve essere un procedimento inverso a quello della tangente. Egli prende spunto da qui per approfondire la cosa ed arrivare a risultati generali. Nell’ottobre del 1674 scrive un’altro lavoro matematico; Schediasma de serierum summis et secriebus quadraticis, dove tenta la soluzione del problema inverso della tangente attraverso la somma della serie delle quadrature. Subito dopo, in una serie di articoli (1675), introduce il simbolo di integrale e quello dei differenziali. Egli stesso si meraviglia del nuovo tipo di calcolo che ha creato (29 ottobre 1675), diverso da quello di Viète come il cielo dalla Terra. Intanto ha conosciuto il matematico e filosofo Malebranche ed ha letto il Dialogo sopra i due massimi sistemi del mondo di Galileo.

      Intanto aveva perfezionato la sua macchina calcolatrice e ne dà una dimostrazione all’Accademia delle Scienze di Parigi con la segreta speranza di essere accolto come membro visto che il matematico Roberval era venuto a mancare (il fatto è che, mentre nella Royal Society di Londra il diventare membri significava pagare una quota, per l’Accademia delle Scienze di Parigi, diventare membro significava prendere uno stipendio e Leibniz voleva avere lo stipendio

dall’occupazione che più gli piaceva). Ma nel 1676 lasciò la Francia, per recarsi ad Hannover in Sassonia ad occupare quel posto di consigliere e bibliotecario del duca di Brunswick, passando per l’Inghilterra (dove Collins, il bibliotecario della Royal Society, gli permette di redigere degli estratti dei manoscritti del De analysi e dell’Historiola di Newton) e l’Olanda (dove incontra il biologo fondatore della microbiologia, van Leeuwenhoeck, e Spinoza con il quale passò un mese intero a discutere, che avranno grande influenza sul suo pensiero, anche se in seguito Leibniz minimizzerà molto soprattutto i suoi rapporti con Spinoza). Il duca era un appassionato di scienze e Leibniz si trovò molto bene alla sua corte arricchendo la biblioteca di ogni testo scientifico reperibile, anche raro. Iniziò ad Hannover un lungo e fecondo periodo di viaggi e di lavoro.

        Nello stesso 1677 pubblicò sotto pseudonimo un’opera giuridica, De jure suprematus ac legationis principum Germaniae, nella quale difese il diritto dei singoli stati tedeschi di fronte a quelli dell’Impero centrale (il Sacro Romano Impero). Intanto il duca per cui lavorava si era convertito al cattolicesimo ma era un liberale in fatto di religione e non si privò dei servizi di Leibniz. Il quale, per parte sua, era uno strano luterano se immaginava il Papa come capo spirituale di tutti i cristiani (in ogni caso, per tutta la sua vita, Leibniz perseguì il sogno dell’unificazione delle chiese ed a tal fine lavorò molto in incontri per l’intera Europa). In quest’anno ricevette una delle due lettere che Newton gli inviava tramite Oldenburg. In essa, con il solito sistema di comunicazione cifrata, gli comunicava i segreti del suo metodo delle flussioni. Ad essa Leibniz rispose comunicandogli i suoi avanzamenti con il metodo dei differenziali. Intanto, mentre si occupava dell’amministrazione del ducato con alcuni progetti di drenaggio di terre mediante mulini a vento, riprese il suo lavoro giovanile, De arte combinatoria, rielaborandolo ed arricchendolo in tre scritti: Elementa Characteristicae Universalis, Elementa calculi, Calculi Universalis Elementa. Collegato a questi lavori ve n’è anche uno di logica, l’Introductio ad encyclopaediam arcanam.

        Nel 1680, alla morte del duca  Johann Friedrich, il nuovo duca, il principe vescovo Ernst August (fratello dell’altro), lo mantenne al suo posto. Diminuirono i finanziamenti per la biblioteca, non fu accettato il suo piano di riarmo del ducato e neppure quello per la creazione di un’Accademia ad imitazione di quella francese ma Leibniz passò sotto la protezione della Principessa Sofia, moglie del duca ed appassionata di filosofia, alla quale Leibniz restò legato da profonda amicizia per tutta la vita. Mentre continuava a sperare in una sua chiamata presso l’Accademia di Francia o in quella di Vienna, iniziò a dedicarsi ai suoi lavori filosofici entrando in corrispondenza con molte personalità della cultura tedesca. Con essi partecipò alla fondazione (1681) di una rivista dal titolo Acta Eruditorum, diventando, con il filosofo Mencke, il principale redattore (la rivista era in latino con lo scopo di proporsi come ideale di unificazione della cultura europea).

        Nel 1682 negli Acta eruditorum pubblicò Unicum opticae, catoptricae et dioptricae principium. Nel 1683 redasse un pamphlet anonimo (su incarico dell’Elettore), Mars christianissimus, contro Luigi XIV perché non era accorso a sostegno di Vienna assediata dai turchi. Nel 1684 pubblica, ancora negli Acta Eruditorum, un altro fondamentale lavoro di matematica, Nova methodus pro maximis et minimis e, subito dopo, Meditationes de cognitione, veritate et ideis. Non cita Newton anche perché, come vedremo, la sua strada verso gli infinitesimi è radicalmente diversa da quella del fisico inglese. Nel 1685 l’Elettore gli assegna un vitalizio in aggiunta allo stipendio che aveva e lo nomina suo consigliere a vita. Nel 1686 scrive il suo importante Discours de Metaphysique (inedito fino al 1845) che è una raccolta e rielaborazione dei suoi pensieri filosofici sviluppati fino ad allora ed anche la Brevis demonstratio erroris memorabilis Cartesii (vedi paragrafo 2.1 dell’articolo su Huygens)⁽¹⁾ in cui innesta la polemica sul cosa si conservi, se mv o mv². Insieme alla cura delle cose di suo interesse, egli deve anche essere ossequiente con chi gli dà lo stipendio ed allora deve curare gli affari di Stato tra cui lo sfruttamento di un bacino minerario (lo Harz) e le trattative con l’Olanda e la Compagnia delle Indie per lo sfruttamento delle ricchezze coloniali provenienti da Sumatra ed una corrispondenza, gradita, con Sofia Carlotta, figlia della sua protettrice duchessa Sofia e futura regina di Prussia. Oltre a ciò  deve accettare l’incarico di costruire una genealogia della famiglia Brunswick-Lunebourg (da utilizzare a livello imperiale per pretendere maggiore potere) per assolvere il quale deve peregrinare per le biblioteche di mezza Europa. Iniziò dalla Germania dove capì che i Brunswick avevano dei legami di parentela con gli Este e quindi, dopo essere passato per Vienna, nel 1689 si recò in Italia per restarvi oltre un anno. Iniziò da Venezia, quindi seguì a Roma per studiare documenti alla Biblioteca vaticana e dove, tra gli altri, conobbe Padre Grimaldi, noto anche per le sue ricerche di ottica. Quindi si recò a Napoli, Pisa, Firenze (dove conobbe Vincenzo Viviani), Bologna (dove conobbe Marcello Malpighi), Ferrara, Modena (dove il granduca Francesco II gli dette libero accesso alla Biblioteca) e Loreto. In questo periodo scrisse il Phoranomus seu de potentia et legibus naturae e lesse i Philosophiae Naturalis Principia Mathematica di Newton.In Italia, come accaduto già a Descartes, ebbe un’avventura che avrebbe potuto costargli la vita.

        Dovendo recarsi da Venezia nell’allora isola di Mesola nel delta del Po, si servì di una piccola imbarcazione. Appena partiti su un mare calmo, si scatenò una violenta tempesta che fece pensare al proprietario dell’imbarcazione di aver fatto salire a bordo un eretico. Comunicò la cosa agli uomini di bordo che, parlando tra loro a voce alta pensando che il passeggero tedesco non capisse, furono d’accordo trovando come soluzione quella di gettarlo in mare. Per risolvere il grave problema Leibniz tirò fuori dalla tasca un rosario e cominciò a pregare in

latino a voce alta. L’equipaggio si convinse che Leibniz non era eretico e non seguì nel primitivo proposito.

        Tornato ad Hannover, dopo essere passato per Vienna in cui scrisse De causa gravitatis, et defensio sententiae auctoris de veris naturae legibus contra Cartesianos e iniziata la compilazione della genealogia richiesta (che farà iniziare prima del diluvio con un prologo in cui ricostruisce la storia primitiva della Terra con studi sulle rocce, le erosioni e molto altro tanto da essere considerato a metà Ottocento come il creatore della geologia), utilizzerà tutti i documenti di diversa natura raccolti (bolle, decreti, leggi, manifesti, dichiarazioni di guerra, trattati di pace, …) per pubblicarli in vari tomi ad iniziare con il Codex juris gentium diplomaticus (1693) con una prefazione di grandissimo interesse nella quale sostenne che solo partendo dai documenti è possibile fare storia. Elencando poi la moltitudine dei trattati di pace che si susseguono con grande frequenza commenta desolato che l’unica vera pace è tra i morti.

        E’ il 1691 quando viene nominato  direttore della biblioteca di Wolfenbuttel. Pubblica in quest’anno sul Journal des Sçavans la Lettre sur la question, si l’essence du corps consiste dans l’etendue dove sostiene la sua concezione della materia costituita da forza e non da mera estensione (risultando il fondatore del dinamismo fisico  che sarà successivamente sviluppato da G. R. Boscovich, Schelling e Faraday). L’anno seguente: pubblica la seconda parte del precedente lavoro, Regle generale sur la composition des mouvemens, sempre sul Journal des Sçavans (che sarà ancora arricchita nel 1695 con lo Specimen dynamicum in cui la sua fisica è messa in connessione con la metafisica e con il Systeme nouveau de la nature et de la communication des substances, aussi bien que de l’union qu’il y a entre l’âme et le corps in cui dà fondo alla sue concezioni metafisiche); inizia una corrispondenza sia con l’astronomo inglese Halley che con il matematico francese de l’Hôpital. Scrive inoltre l’ Essay de dynamique che fa presentare all’Accademia di Parigi. La dinamica è qui presentata sulla base del concetto di forza che ormai è concetto noto per essere stato introdotto da Newton nei Principia. Nel 1694 perfeziona il suo concetto di materia intesa come forza attiva, con un altro articolo per gli Acta eruditorum, la  De primae philosophiae Emendatione et de Notione Substantiae e costruisce una macchina calcolatrice ancora più potente (riesce a fare moltiplicazioni di 12 cifre).

        Nel 1696 muore l’Elettore Ernst August e gli succede il figlio Georg Ludwig (che nel 1715 diventerà Giorgio I d’Inghilterra) che non stima Leibniz perché, a suo giudizio, è dispersivo ed inconcludente (in particolare il nuovo Elettore non ammette che Leibniz non abbia ancora terminata quella genealogia e poiché Leibniz era spesso in viaggio tra Berlino e Vienna, da un certo punto in poi – 1705 –  glielo proibì con qualche successo perché nel 1707 uscirà il primo volume della genealogia, Scriptores rerum Brunsvicensium). Continua a mantenerlo a corte per il prestigio che il suo nome ha ancora in tutta Europa. Ma, nei fatti, se si rilegge un poco quanto ho scritto e se dovessi seguire ogni sua attività fino alla sua scomparsa, non finirei più. Posso solo elencare le cose di maggiore interesse che egli farà da questa fine secolo al 1716, anno della sua morte.

        Finalmente, nel 1700, viene nominato membro dell’Accademia delle scienze di Parigi e, nello stesso anno riesce a fondare la Società delle Scienze di Berlino. Nel 1707 inizia a scrivere i Nouveaux essais sur l’entendement humain (una risposta, pubblicata postuma nel 1765, all’ Essay Concerning Human Understanding che Locke aveva scritto nel 1690) e pubblica a Parigi un’importante articolo sull’algebra binaria, Explication de l’arithmetique binaire, qui se sert des seuls caracteres 0 et 1. Nel 1708 inizia la grave e lunga polemica sull’invenzione del calcolo infinitesimale con una lettera aperta alla rivista della Royal Society, Philosophical Transactions, che il fisico inglese Keill  invia ad Halley. In essa si sostiene che il calcolo è dovuto esclusivamente a Newton che è stato plagiato da Leibniz. In realtà la polemica era iniziata nel 1695 e ribadita nel 1699 dal vecchio John Wallis (sempre suscettibile sui diritti inglesi di priorità, come dice A. R. Hall). Due anni dopo pubblica anonimamente in Olanda la sua opera teologica più completa, la Teodicea (Essais de Theodicee sur la bonté de Dieu, la liberté de l’homme et l’origine du mal)⁽³⁾. Intanto monta la polemica con gli inglesi sul calcolo. Leibniz chiede che intervenga la Royal Society la quale nomina una commissione per studiare il caso.

        Avevo accennato che Leibniz aveva a corte una protettrice, la principessa Sofia, moglie dell’Elettore Ernst August. La scomparsa nel 1705 della sua protettrice lo aveva lasciato più scoperto ai voleri del nuovo Elettore. Ma la figlia, Carlotta Cristina Sofia di Brunswick, sposandosi con il figlio dello zar Pietro il Grande di Russia, aveva aperto a Leibniz nuove possibilità di lavoro perché venne immediatamente richiesto da quella corte per organizzare le scienze in Russia. Anche Sofia Carlotta divenne amica di Leibniz e, quando questi parlava alla Principessa dei suoi infinitamente piccoli, ella rispondeva che li conosceva bene nella sua corte.

        Nel 1712 la commissione della Royal Society fa conoscere le sue risultanze pubblicando a cura di J. Collins un Commercium epistolicum, la raccolta della corrispondenza tra Newton, Wallis, Oldenburg e Leibniz. Alla fine di tale documentazione epistolare la commissione sentenzia che  a Newton va assegnata la l’invenzione del calcolo infinitesimale:

… riteniamo che Newton sia stato il primo inventore di questo metodo, e che quindi Keill, nel sostenere questa stessa tesi, non ha arrecato nessuna ingiuria o calunnia a Leibniz. Rimettiamo al giudizio della Società se gli estratti delle lettere e gli altri documenti ad esse connessi debbano venir pubblicati insieme a quelli, concernenti questa stessa questione …

(Ricevutane comunicazione il 24 aprile 1712, la Società Reale ordinò la pubblicazione delle lettere, dei manoscritti e della sentenza del consesso, come di alcuni passi utili a chiarificare questa questione, contenuti negli “Acta Eruditorum”).
 

        Il fatto sorprendente è che la commissione di cui sopra non chiese la documentazione di cui disponeva Leibniz⁽²⁾.

        Nel 1714 scrisse le opere più complete del suo pensiero filosofico, i Principes de la Nature et de la Grace fondées en raison e  Principes de la  Philosophie ou Monadologie (il titolo Monadologie non è di Leibniz ma dell’editore) che saranno pubblicate postume nel 1720. Ma questa grande soddisfazione per lui viene subito gelata da una nuova proibizione da parte dell’Elettore di muoversi fino a che non ha finito di scrivere quella grana che fu sempre per lui la genealogia (quando morì, Leibniz era arrivato all’anno 1009 di tale genealogia). Aveva quasi 70 anni, Leibniz, e questo divieto gli pesò moltissimo. Passò praticamente segregato gli ultimi due anni di vita. Morì nel 1716 praticamente dimenticato. La corte era al seguito di Giorgio I in un padiglione di caccia vicino ad Hannover e nessuno si recò al suo funerale, la Royal Society di Londra per motivi evidenti non fece la rituale commemorazione di un suo membro e per colmo anche la Società delle Scienze di Berlino tacque. Solo il cartesiano abate Fontenelle gli tributò un Elogio all’Accademia di Parigi con il paradosso che la commemorazione venne proprio da coloro che egli più aveva osteggiato per le loro posizioni religiose, politiche e cartesiane ma probabilmente contò di più la comune posizione antinewtoniana⁽⁴⁾.

Una pagina autografa della Monadologie di Leibniz

2.2 – IL CALCOLO INFINITESIMALE

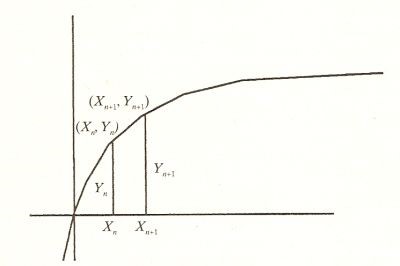
        Quando Leibniz iniziò a lavorare in matematica, intorno al 1670, la via degli sviluppi in serie per lo studio di curve anche complesse era quella che sembrava offrire i maggiori sbocchi. Come Newton, anche Leibniz concentrò i suoi primi studi matematici sullo sviluppo in serie infinite. Con tali serie risolse alcuni problemi (somma dei reciproci dei numeri triangolari, triangolo armonico, …), il primo dei quali gli era stato proposto da Huygens, e prese familiarità con esse. Il suo calcolo differenziale deriva dalla differenza di successioni ed il suo calcolo integrale deriva dalla somma di successioni. Egli racconta proprio questo in una lettera a Wallis: La prima idea l’ho avuta quando, considerando le differenze e le somme nelle serie dei numeri, mi accorsi che le differenze corrispondevano alle tangenti  e le somme alle quadrature. Infatti una curva è una poligonale con infiniti lati ognuno dei quali ha lunghezza infinitesima. In tal modo alla curva

Le differenze finite:

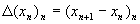
 e le somme    

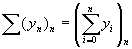
che origineranno differenziali ed integrali

risultano associate differenti successioni di numeri, quella delle ascisse, quella delle ordinate, quella della lunghezza dei segmenti, … A questo punto, poiché il calcolo a quell’epoca aveva ancora connotazioni geometriche, il suo interesse si spostò alla cicloide ed ai lavori di Pascal in proposito. In occasione della lettura (1673) dell’opera matematica di Pascal (Traité des sinus du quart de cercle⁽⁵⁾), lo stesso Leibniz ci racconta che ebbe una sorta di folgorazione. Egli si rese conto che: 

1) per determinare la tangente ad una curva occorre considerare le differenze delle ordinate e delle ascisse quando tali differenze diventano infinitamente piccole e che 

2) per determinare una quadratura occorreva considerare dei rettangoli infinitamente piccoli sottesi alla curva medesima, tutti da sommare (summa omnes) ed infine che

3) le due operazioni sono correlate in modo che l’una risulta l’inverso dell’altra.

        L’ispirazione sembra gli sia venuta dal riflettere sul confronto dei triangoli caratteristici proposti da Barrow per trovare una tangente ad una curva e da Pascal per trovare la quadratura dei seni. Barrow esponeva un suo metodo per trovare le tangenti ad una curva. Il metodo si basa sul triangolo differenziale (o triangolo caratteristico)riportato in figura. Per trovare la tangente si opera nel modo seguente (riporto quanto riassume Boyer).

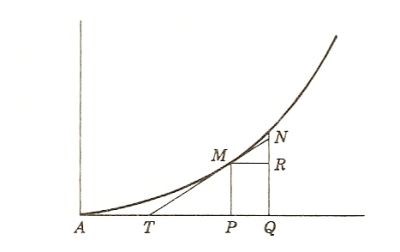
Sia M un punto di una curva espressa (nella notazione moderna) da un’equazione polinomiale f(x, y) = 0, e T sia il punto di intersezione della tangente desiderata MT con l’asse delle x. Barrow segnava allora “un arco indefinitamente piccolo, MN, della curva”; tracciava poi le ordinate dei punti M e N, e per M tracciava una retta MR parallela all’asse delle x. Indicando poi con m l’ordinata di M, che era nota, con t la sottotangente PT, che si desiderava conoscere, e con a ed e i lati verticali e orizzontali del triangolo MRN, Barrow faceva notare come il rapporto a:e fosse uguale al rapporto m:t. Oggi diremmo che il rapporto a:e per punti infinitamente vicini esprime la pendenza della curva. Per trovare questo rapporto Barrow … sostituì x e y nell’equazione f(x,y) = 0 rispettivamente con x + e e y + a; poi nell’equazione risultante trascurò tutti i termini non contenenti a o e (dal momento che questi erano uguali a zero) e tutti i termini di grado superiore al primo in a ed e, e infine sostituì a con m ed e con t. Da ciò si ottiene la sottotangente in termini di x e m, e se si conoscono x e m, la quantità t risulta determinata.

        Mentre il triangolo proposto da Pascal  è riportato in figura seguente. Con esso, per trovare la quadratura del seno, si operava nel modo riassunto da Boyer:

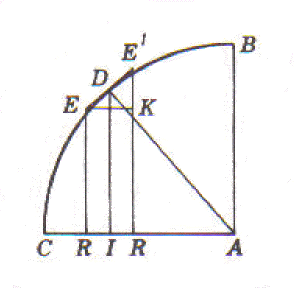
Se EDE’ è la tangente in D al quadrante unitario BDC, allora AD sta a DI come EE’ sta a RR ossia a EK. Per un intervallo RR molto piccolo si può considerare il segmento EE’ come virtualmente uguale all’arco della circonferenza compreso tra le ordinate ER.

        Questa sorprendente similitudine tra i due metodi per studiare problemi apparentemente diversi, fece riflettere e studiare Leibniz. Tre anni dopo, nel 1676, egli fa sapere con una lettera al segretario della Royal Society di Londra, Oldenburg, di essere in possesso di un metodo per trovare le radici delle equazioni e le aree delle figure mediante serie infinite che differisce completamente da quello di Newton. 

        Leibniz si era già reso conto che una delle difficoltà del calcolo era il simbolismo che differiva continuamente. Egli, a partire dal 1675, iniziò una fecondissima opera che tendeva a fornire l’analisi di tale simbolismo. Per indicare le quadrature era usata l’espressione summa omnes (per indicare la somma di tutti i rettangolini in cui si suddivideva una data figura). Tale espressione veniva abbreviata in omn e si premetteva all’ordinata di una curva. Leibniz pensò bene di utilizzare per la parola somma la sua iniziale, una S che, all’epoca, si scriveva  ∫ . Con tale notazione, quanto detto diventa: ∫ y. Ma questo modo di scrivere non rappresentava la somma di aree ma solo di ordinate. Tale ordinata generica andava moltiplicata per la sua base infinitesima (che Leibnix indicò con dx), comune a tutti i rettangolini, al fine proprio di avere l’area del rettangolino generico. In tal modo la notazione diventava ∫ y.dx.  E’ questo il simbolismo che oggi si usa universalmente e che va sotto il nome di integrale. Restava il problema della distinzione tra integrale definito ed indefinito. In questo periodo, tutti gli integrali erano considerati definiti, benché non ci fosse una speciale notazione per i limiti; così la notazione  ∫ y.dx  rappresentava ciò che ora sarebbe scritto come:

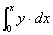
        Leibniz sapeva bene che una tale operazione abbassa il grado di una data funzione, pertanto, nel realizzare l’operazione inversa divideva per una d. Cioè: se risulta ∫ y = x;      l’operazione inversa ci deve fornire y = x/d. Più avanti nel tempo trasformò definitivamente quell’ x/d  in  dx (più tardi, nel 1680, dirà: queste dx e dy si prenderanno come infinitamente piccole, o si deve intendere che i due punti della curva sono separati da una distanza minore di qualunque lunghezza data e nel 1686, dopo che si era accorto che altri matematici superficialmente facevano a meno di scrivere il dx, affermerà: raccomando di non omettere dx … errore frequentemente commesso e che impedisce di andare più oltre). E’ da notare che, quando realizzava queste cose, Leibniz già aveva le idee chiare su alcune regole del calcolo. Egli, ad esempio, poneva i fattori costanti fuori del segno di integrale e trasformava la somma di integrali di differenti funzioni in integrale della somma delle funzioni, … Osservo a parte che  è dovuta allo stesso Leibniz la definizione di funzione (1694): Si dice che y è funzione di x quando a certi valori di x, corrispondono valori determinati di y.

        E’ molto importante notare che l’agilità di tale simbolismo, facilitò lo stesso Leibniz ad elaborazioni successive permettendo quasi di astrarsi dai singoli problemi per considerare il calcolo come un metodo generale che prescindeva dalle funzioni in gioco. Anche sull’assegnare i nomi alle singole operazioni fu fondamentale l’opera di Leibniz. Egli chiamò calculus differentialis quello che permetteva di trovare le tangenti, chiamò poi calculus summatorius o calculus integralis (l’aggettivo integrale fu suggerito da Jacques Bernouilli nel 1690 ed accettato da Leibniz)quello che realizzava le quadrature (il calcolo di aree o volumi). 

        Come accennato, Leibniz pubblicò il suo calcolo infinitesimale nel 1684, negli Acta Eruditorum, con il titolo Nova methodus pro maximis et minimis, itemque tangentibus, qua nec irrationales quantitates moratur. Tale lavoro di solo 8 pagine è l’esposizione completa della  teoria (con alcuni esempi) del calcolo 

di Leibniz. Scrive Leibniz:

Sia a una quantità data costante, sarà 

da = 0 

e 

dax = adx.

Se abbiamo 

y = v

(…) sarà 

dy = dv.

E passa subito a fornire le regole del calcolo:

Addizione e sottrazione:

se si ha 

z – y + w + x = v 

sarà 

d(z – y + w + x) =  dv = dz – dy + dw + dx.

Moltiplicazione:

dxv = xdv + vdx

ovvero, posto y = xv, sarà 

dy = xdv + vdx.

Divisione:

ponendo z = v/y si ha

   .

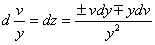
Quanto a[ll’uso corretto de]i segni è da notarsi  questo: quando nel calcolo, viene sostituito alla lettera semplicemente il suo differenziale, si devono conservare gli stessi segni, e scrivere + dz in luogo di + z e – dz, in luogo di – z, come appare dall’addizione e dalla sottrazione esposta poco prima. (In riferimento ad una curva che Leibniz ci presenta, egli discute qui le sue convessità, concavità e flessi).

Potenza:

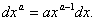
Ad esempio:

dx³ = 3x²dx

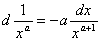
Ad esempio, se risulta

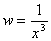
sarà 

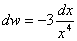
Radice:

(…)

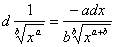
Sarebbe bastata la regola della potenza numerica intera per determinare i differenziali tanto delle frazioni come delle radici; la potenza infatti diviene una frazione quando l’esponente è negativo, e si muta in radice quando l’esponente è frazionario: ma ho preferito dedurre io stesso queste conseguenze piuttosto che lasciarle ad altri da dedurre, dal momento che sono assai generali e s’incontrano spesso, e in un argomento per sé stesso complesso è preferibile pensare alla facilità.

Dalla conoscenza di questo Algoritmo, così lo chiamo, o di questo calcolo, che chiamo differenziale, si possono ottenere tutte le altre equazioni differenziali per mezzo dell’algebra comune, così anche i massimi ed i minimi, così come le tangenti, , in modo tale che non risulta necessario considerare a parte le frazioni o gli irrazionali o altri vincoli, come era necessario fare con i Metodi pubblicati fino ad ora [Castelnuovo, pagg. 163-168]

        E per Leibniz gli infinitesimi di ordine superiore (dx.dx, dx.dy, ….) andavano trascurati. 

        Il calcolo differenziale, qui esposto nel 1684, verrà completato due anni dopo, sempre negli Acta Eruditorum, con un nuovo articolo dal titolo De geometria recondita et Analysi indivisibilium atque infinitorum, Addenda his quae dicta sunt in Actis a. 1684, Maji, p. 233; Oct. pag. 264; Decemb. p. 585. Ora Leibniz tratta del calcolo integrale, ricavato come operazione inversa a quella che forniva le tangenti, il calcolo differenziale (questa relazione inversa è argomento del teorema fondamentale del calcolo infinitesimale). Dice Leibniz:

Il metodo di investigare Quadrature indefinite (…) è per me solo un caso particolare (e, certamente, il più facile) di un problema molto più grande, che chiamo metodo inverso delle tangenti, dentro il quale è contenuta la maggior parte di tutta la geometria trascendente  (…)

geometria che risultava esclusa dal metodo di Cartesio. E Leibniz passa ad esemplificare la potenza del suo metodo, facendo vedere che quanto prima si otteneva in modo laborioso, ora risulta molto più semplice (offro qui una approssimazione al tema, la cui utilità è evidente). Sia data la curva di figura che ci presenta Leibniz, nella quale compare il triangolo caratteristico o differenziale:

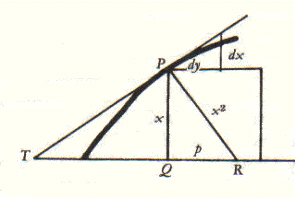
Sia “x” l’ordinata, “y” l’ascissa, e sia “p” l’intervallo tra la perpendicolare e l’ordinata. Con il mio metodo si vede subito che risulta:

pdy = xdx,

trasformata questa equazione differenziale in una somma, si otterrà:

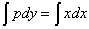
Da ciò che esposi nel metodo delle tangenti, è evidente che  d(1/2)x² = xdx; pertanto la reciproca è

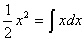
(così come le potenze e le radici nei calcoli comuni, le somme e le differenze o ” ∫ ” e “d” sono reciproche). Otteniamo, come conseguenza

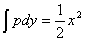
che era ciò che volevamo dimostrare.

        Senza dilungarmi troppo, ricordo che a Leibniz è dovuto il differenziale della lunghezza di una curva piana:

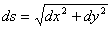
ed il volume di un solido di rivoluzione intorno ad un asse  

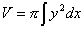
(se l’asse è l’asse x). Egli introdusse e studiò anche i differenziali parziali, l’integrale multiplo, le equazioni differenziali a variabili separabili, le equazioni differenziali omogenee e la soluzione delle equazioni differenziali del primo ordine.

        E’ certo che la struttura del calcolo di Leibniz era molto carente, soprattutto se confrontata con le elaborazioni successive dei Bernouilli (con i quali Leibniz intrattenne una fitta corrispondenza), degli Eulero (1707 – 1783), dei Lagrange (1736 – 1813), dei Cauchy (1789 – 1857), ma è altrettanto vero che, le cose che egli scrive sono, per noi, una boccata di freschezza in una matematica che si stava incartando su se stessa. E’ comunque da osservare che ci vorranno circa 100 anni per conquistare il rigore in matematica: esso si può datare con le Réflexions sur la métaphysique du calcul infinitésimal di Lazare Carnot e la Théorie des fonctions analytiques di Lagrange ambedue del 1797.

        Prima di chiudere questo paragrafo che riguarda la matematica in Leibniz un cenno, ma solo un cenno, occorre dare ad altri contributi dati alla matematica dal filosofo tedesco.

       Le sue prime ricerche in matematica riguardarono i triangoli armonici H.

quelli cioè che godono delle seguenti proprietà

Hij = H_i-1,j – H_i,j+1

Hij = H_i,j-1 – H_i-1,j-1

e ciò vuol dire che somme lungo la diagonale di 45° sono somme di differenze come nell’esempio seguente:

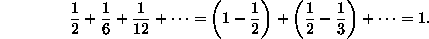
ed ancora,

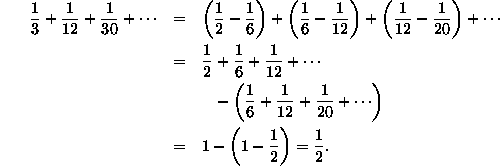
Moltiplicando poi per 3 otteniamo i numeri piramidali:

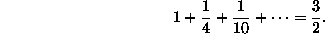
2.3 – LA FISICA

        Molte delle cose che riguardano i contributi di Leibniz allo sviluppo di alcuni concetti di fisica, le ho discusse quando ho trattato di Huygens. Resta ora da fornire un quadro più organico del pensiero di Leibniz sull’insieme dei concetti di fisica fino al suo tempo sviluppati.

        Prima di entrare in dettagli è bene dire che se, anche in modo meno vistoso, siamo di fronte ad un personaggio come Descartes che impregna di Dio tutto l’esiastente. Ed a questo punto mi risulta complicato stabilire se conviene discutere lo sviluppo cronologico delle idee di Leibniz, tenendo conto della difficoltà dei molti inediti che in qualche modo vanno considerati (ma con ce cronologia?), o se partire dalle sue concezioni metafisiche, alla luce delle quali è più completa la lettura del suo pensiero. Probabilmente questa seconda strada dirime molte possibili controversie che la prima strada comporta e comunque nel seguire questa strada non tolgo nulla alla cronologia perché colloco le opere da cui traggo le citazioni nel momento in cui sono state elaborate.

2.3.1 – UN POCO DI METAFISICA COME INTRODUZIONE

        Parto quindi da alcune definizioni che Leibniz ci presenta nel suo  Discours de Metaphysique, scritto nel 1686 (ma edito nel 1845) quando aveva 40 anni che, data la precocità del personaggio, si può ritenere un’età matura. E tali definizioni dovranno essere viste alla luce di altre cose che Leibniz dice nella sua Monadologie scritta quando aveva 69 anni. C’è da dire preliminarmente che la tendenza generale di quei tempi, a partire dal Sedicesimo fino a Diciottesimo secolo inoltrato, era di considerare le leggi fisiche come leggi stabilite se non dettate direttamente da Dio. Sta al filosofo, che spesso è teologo, interpretarla alla luce proprio di quella che si ritiene essere la volontà di Dio. Col passare degli anni però e per fortuna questa onnipresenza di Dio va cambiando carattere. Ancora con Descartes e con Leibniz i confini tra fisica e metafisica erano indefiniti. Dopo questi filosofi le cose vanno cambiando con sforzi giganteschi da parte dei filosofi che sempre più erano della natura e sempre meno della metafisica. Ciò non vuol dire che entra nella fisica l’ateismo ma solo che piano piano i ruoli vanno distinguendosi e la teologia prima, come detto, onnipresente inizia a comparire solo all’inizio o alla fine di un lavoro scientifico. Una sorta di omaggio di rito che in genere riguardava la Creazione con parole del tipo: Tutte le meraviglie della natura sono state create da Dio. Sta a noi studiarle e capirne il funzionamento per maggior gloria del Signore. Ed a volte con Dio che provvede a qualche possibile disgrazia o mancanza ed interviene con la sua bontà a dare spinte ed aiutare a tirare avanti. Poi, di seguito, l’opera scientifica in cui Dio era dimenticato. Ancora più avanti nel tempo, anche quella presenza di rito è scemata fino alla conquista della competa separazione della scienza dalla teologia. Ma ora stiamo discutendo dell’ultimo filosofo che prevede il Dio onnipresente, quello che passerà il testimone a consapevolezze scientifiche più mature, quello che se si fa un poco di attenzione, alla fine della sua vita risulterà addirittura fuori moda, fuori dal mondo che avanzava nella direzione di una scienza matura ed autonoma da qualunque orpello (solo pochi anni dopo sarà Lagrange a sostenere apertamente che nella sua opera si sarebbe astenuto da ogni speculazione metafisica e teologica perché estranea ed anzi dannosa alla scienza, verrà poi Laplace e molti altri).

        Leibniz, come dicevo, nel suo Discours de Metaphysique si sofferma a definire e chiarire alcuni concetti di carattere eminentemente teologico. Tra questi, all’epoca, vi erano concetti che sono  anche alla base della teoria fisica, come quelli di spazio, tempo, movimento, sostanza, …

        Dopo aver discusso della perfezione e bontà di Dio e del fatto che ha realizzato il meglio per tutti noi, ma anche dopo aver differenziato le sostanze dagli accidenti richiamando la non disprezzabilità degli aristotelici (siamo ancora lì!), Leibniz ci parla di sostanze intersecando vistosamente la metafisica con la logica. La sostanza è alla base delle sue speculazioni con alcune specificazioni di notevole importanza. Si parte infatti dalla sostanza individuale, quella che contiene in sé (e permette di dedurre da sé) tutti i possibili predicati e da essa si tratta di capire come e dove troviamo tale sostanza individuale. La sostanza individuale è quindi come un mondo intero e come uno specchio di Dio o se si vuole di tutto l’universo che ognuna esprime della sua maniera. Intanto, contrariamente a Descartes, per Leibniz l’estensione non può essere una caratteristica di una sostanza. Infatti l’estensione implica una pluralità e la sostanza è solo individuale. Quindi l’estensione deve appartenere solo ad un aggregato di sostanze. Queste sostanze devono essere quindi infinite ed ognuna di esse deve essere appunto un microcosmo che egli, con reminiscenza bruniana, chiama monadi. Per le caratteristiche dette la monade è un’anima o, come diranno meglio i continuatori di questa posizione filosofica (dinamismo) trasferendola alla fisica, un centro di forze (o, perché no?, un differenziale). Forzando un poco il pensiero di Leibniz si potrebbe pensare la monade come un atomo immateriale proprio perché non ha estensione ma pensiero allo stato puro. Questa posizione, discutibile quanto si vuole, si inserisce in quel filone, che avrà molti seguaci, di coloro che negano la materia al posto della quale vedono forze o equazioni (come diranno Mach ed Heisenberg) con Leibniz che vedeva solo anime. Le monadi, questa volta in linea con Descartes, poiché non hanno finestre, non possono interagire tra loro e ciò creerà un qualche problema di consistenza logica sia nel campo dell’interazioni tra corpi nella dinamica, sia nel campo della percezione. Questa seconda difficoltà era così discussa da Leibniz. Ogni monade rispecchia in sé l’intero universo e ciò avviene non perché l’universo influisca su di essa ma perché questo è ciò che ha costruito Dio. Esiste una armonia prestabilita tra i cambiamenti che avvengono tra diverse monadi ed è l’armonia che dà l’apparenza delle interrelazioni (come più sveglie che suonano contemporaneamente ma non perché hanno relazioni tra loro) anche se risulta complicato capire come fa una monade ad accorgersi dell’altra e come, ad esempio, la monade anima dell’uomo si accorge che il comando alle monadi braccio di sollevarsi per grattare la testa sia stato eseguito. Dice Leibniz (Proposizione 14 del Discours de Metaphysique):

Dio produce diverse sostanze secondo le diverse visioni che ha dell’universo e per l’intervento di Dio la natura propria di ogni sostanza fa che ciò che accade ad una risponda a ciò che accade a tutte le altre, senza che agiscano le une sulle altre.

… e poiché Dio vede sempre bene, anche le nostre percezioni sono corrette ma sono i nostri giudizi che sono nostri che ci ingannano …

introducendo elementi che poi saranno ripresi, con significato opposto, da Laplace:

tutti i nostri pensieri e tutte le nostre percezioni future non sono se non conseguenze, anche se contingenti, di tutti i nostri pensieri e delle nostre percezioni precedenti se io fossi capace di considerare tutto ciò che succede o mi appare ora, potrei vedere in esso tutto ciò che mi accadrà o apparirà un in un dato momento.

        Le sostanze, indivisibili, non si creano e non si distruggono, solo un atto di Dio potrebbe provocare tali cose. Anche lo spazio, così come appare ai sensi e come discutiamo in fisica, è costituito da monadi disposte tridimensionalmente e, sembra di capire, che queste monadi hanno una qualche posizione nello spazio, anche se, dicendo questo, violentiamo il pensiero di Leibniz perché non ha senso parlare di spazio indipendentemente dalle monadi. Non vi è vuoto perché sono le monadi che occupano tutto ed ogni punto è occupato da una ed una sola monade. Dice Leibniz all’inizio della Monadologie:

La monade non è che una sostanza semplice che entra nei composti; semplice cioè senza parti. E’ necessario che vi siano sostanze semplici dato che vi sono composti, giacché il composto non è che un ammasso o aggregato di semplici. Ora, dove non vi sono parti, non vi è nemmeno estensione, né figura, né divisibilità possibile; e queste monadi sono i veri atomi della natura: in una parola gli elementi delle cose

e così ripiombiamo a Zenone ed ai suoi paradossi se solo ci chiediamo come fa un oggetto composto da oggetti senza dimensioni ad avere dimensioni. Solo l’analisi infinitesimale ci può aiutare con i differenziali appunto ma, appunto, siamo in matematica e non in fisica.

        Nel portare avanti questi ragionamenti che sembrano non aver nulla a che fare con la fisica, Leibniz doveva opporsi al materialismo di scuola francese, dei Descartes e dei Gassendi e, contemporaneamente definire  uno spazio che fosse radicalmente diverso da quello di Newton. Probabilmente c’è riuscito nel dibattito filosofico ma, con la fisica queste cose non c’entrano nulla o meglio hanno delle ricadute a volte nefaste per l’uso che ne può venire fatto e che ne sarà fatto nel Novecento.

        Dopo averci spiegato come e perché Dio fa miracoli e perché noi non possiamo capire, Leibniz passa a discutere (Proposizione 17) della conservazione della quantità di moto o della forza viva in termini non dissimili dai miracoli cartesiani. Ma, naturalmente, in nome di Dio, ci racconta che Descartes sbagliava perché non si conserva mv ma mv² (la forza, come dice Leibniz). Dice Leibniz:

… Dio conserva sempre regolarmente la medesima forza, e non la stessa quantità di moto, contro i cartesiani ed altri vari.

… usualmente i nostri filosofi si servono della famosa regola secondo la quale Dio conserva sempre la stessa quantità di movimento nel mondo. In effetti è molto plausibile ed in altri tempi io lo ritenevo indubbio. Ma poi ho scoperto in cosa consiste l’errore. E’ che il signor Descartes ed altri molti abili matematici hanno creduto che la quantità di moto, cioè la velocità moltiplicata per la grandezza del mobile [massa, ndr]

che si conserva mentre è la forza viva, cioè il prodotto della velocità elevata al quadrato per la massa del mobile, che si conserva.

Ed è ragionevole che si conservi sempre la stessa forza nell’universo. Infatti, quando si presti attenzione ai fenomeni, si vede bene che il moto meccanico continuo non esiste

perché esiste sempre dell’attrito che lo rallenta e poi ferma e si vede anche che la forza viva di un corpo non scema se non in quanto viene ceduta ad altri corpi. Invece Descartes ed i cartesiani hanno creduto di poter affermare le stesse cose sia per la forza che per la quantità di moto.

        E Leibniz si mette qui, nel mezzo di un trattato di metafisica, a dimostrare la sua tesi aiutandosi con la figura seguente:

        In breve egli riporta qui una dimostrazione che è la medesima riportata in varie sue opere con una piccola variazione che introdurrà nello Specimen dynamicum del 1695quando distinguerà tra  forza morta (forze statiche) e forza viva (forza che agisce con un impulso completo). Egli suppone che un corpo che cade da una certa altezza acquisisce una forza per tornare a salire alla medesima altezza, sempre che si mantenga la direzione, a meno che non vi sia un qualche ostacolo. Occorrerà comunque sempre considerare l’attrito e la resistenza dell’aria. Suppone poi che occorre tanta forza per sollevare all’altezza CD di quattro tese (ogni tesa vale poco meno di 2 metri, ndr) un corpo A di una libbra, quanta ne occorre per sollevare un corpo B di quattro libbre all’altezza di una tesa. E queste affermazioni trovano d’accordo tutti i filosofi suoi contemporanei. E’ allora evidente che, essendo caduto il corpo A dall’altezza CD, ha acquistato una forza esattamente uguale a quella del corpo  B caduto dall’altezza EF. Vediamo ora se anche la quantità di movimento è la stessa dall’una e dall’altra parte. E Leibniz dice qui che Galileo ha dimostrato che la velocità acquistata per la caduta CD è doppia di quella acquistata per la caduta EF anche se l’altezza è quadrupla. Moltiplichiamo ora il corpo A, considerato come 1, per la sua velocità, considerata come 2, il prodotto tra queste quantità, ossia la quantità di moto, risulterà uguale a 2. Moltiplichiamo ora il corpo B, che vale 4, per la sua velocità che vale 1 e, per la quantità di moto otteniamo ora 4. Ciò fa concludere che la quantità di moto del corpo A nel punto D è la metà della quantità di moto del corpo B nel punto F, mentre le loro forze sono uguali. Ciò dimostra che c’è una grande differenza tra forza e quantità di moto come Leibniz voleva dimostrare.

        La forza deve quindi essere valutata per l’effetto che è in grado di produrre, ad esempio, all’altezza alla quale si può far salire un corpo pesante e ciò è molto differente dalla velocità che si possa fornire a tale corpo perché per fornirgli il doppio di velocità c’è bisogno di più del doppio di forza. E ciò può essere detto in altro modo. La quantità di moto non si conserva davvero perché vi sono gli attriti che sottraggono moto. Se così non fosse vi sarebbe moto perpetuo. Ciò vuol dire che la quantità di moto non si conserva sempre. Se invece uno fa riferimento alla sua forza, solo essa, nei trasferimenti, si mantiene sempre. Ma pare azzardato leggere ciò con le conoscenze di oggi che farebbero dare piena ragione a Leibniz.

        Leibniz sottolinea quindi che questo è stato l’errore di Descartes e si stupisce che qualcuno dei suoi seguaci non lo abbia rilevato anche se è possibile che tali personaggi abbiano preso le stesse abitudini dei peripatetici dei quali si ridono, dando più credito ai libri del maestro che alla ragione ed alla natura.

        Nella Proposizione seguente, la 18, Leibniz lega il tema che ha appena finito di trattare alla sua metafisica. Egli dice infatti che la distinzione della forza dalla quantità di moto è molto importante non solo in fisica ed in meccanica ma anche in metafisica per capire meglio i principi del movimento, per capire cioè se esso è reale, anche in relazione ad altri corpi in movimento. E mentre il moto, che si caratterizza con la velocità di un oggetto, è un qualcosa di relativo ai corpi che si prendono in considerazione, la forza può invece essere attribuita con certezza ad uno o ad un altro corpo. E ciò deve farci ripensare alcune posizioni dei filosofi che vorrebbero i corpi costituiti da estensione ed alcune modificazioni (aspetto, grandezza, movimento, …) mentre in essi vi è la forza che li avvicina di più alla metafisica essendo forme invisibili della natura che causano le loro apparenze. Queste considerazioni, secondo Leibniz, dovrebbero riconciliare il meccanicismo di alcuni moderni con la circospezione di alcune persone intelligenti e ben intenzionate che temono di allontanarsi troppo dagli enti immateriali con pregiudizio per la pietà.

        Conseguenza di queste affermazioni così elevate è la Proposizione 19 in cui Leibniz ci dice che le cause finali sono utili nella fisica per togliere dalla testa dei nuovi filosofi che Dio opera per il bene. E’ quindi lì, nelle cause finali che occorre cercare perché Dio si propone sempre il meglio per noi. Potremmo però ingannarci quando volessimo determinare i fini di Dio. Ma l’errore vi sarebbe solo se avessimo voluto limitare la volontà di Dio ad un qualche fine particolare, ad esempio, pensando che Dio ha creato il mondo solo per noi e non anche per l’ammirevole struttura degli animali. Vi sono invece dei filosofi che attribuiscono tutto alla necessità della materia o al caso ed è difficile che tali persone possano essere ritenute intelligenti. Infatti è l’effetto che deve corrispondere alla causa e non è ragionevole introdurre un’intelligenza sovrana ordinatrice per poi dimenticarla ed affidare tutto alle proprietà della materia per spiegare i fenomeni. I nostri filosofi sono troppo materialisti ed anche Platone se la prendeva nel Fedone contro i loro argomenti (Prop. 20).

        Le considerazioni metafisico-fisiche di Leibniz si chiudono con la Proposizione 21. In essa si dice che se nei corpi non vi fosse altro che una massa estesa e nel movimento non vi fosse altro che cambiamento di luogo, e tutto potesse e dovesse dedursi da queste sole definizioni per una necessità geometrica, da questo seguirebbe … che il corpo più piccolo darebbe al più grande che fosse in riposo e con il quale urtasse, la stessa velocità che esso possiede senza perdere neanche un poco della propria; e bisognerebbe anche ammettere molte altre regole simili, totalmente contrarie alla formazione di un sistema. Quando a tutto ha provvisto la sapienza divina fornendo la conservazione della forza.

        E’ doveroso, alla fine di questa brevissima rassegna su come in Leibniz fisica e metafisica erano legate tra loro, riportare come Jammer [bibl. 26] riassume questa vicenda:

Leibniz dichiarò ripetutamente che la sua fisica doveva concordare e armonizzare con le sue dottrine teologiche, senza tuttavia presupporre una mutua compenetrazione: nessun principio spirituale doveva venire applicato nella spiegazione dei fenomeni fisici, né si doveva ricorrere alle leggi fisiche per l’interpretazione di fatti religiosi. Nel dimostrare che un determinato evento religioso è possibile e logicamente compatibile con le leggi della fisica, Leibniz non intende spiegarlo per mezzo di queste. Di conseguenza, se egli fa uso della nozione di massa inerziale, cioè ricorre alla qualità insita della materia che si aggiunge a estensione e a impenetrabilità al fine di mostrare la possibilità fisica del mistero eucaristico, non per questo egli tradisce i suoi principi. “Nella teologia rivelata io cerco di dimostrare non la verità effettiva, ma la possibilità dei misteri … , la possibilità della Trinità, dell’Incarnazione e dell’Eucarestia.“

2.3.2 – PASSIAMO ALLA FISICA

            Ho dovuto esporre quanto visto nel paragrafo precedente, altrimenti non saremmo stati in grado di cogliere compiutamente il pensiero di Leibniz. Siamo in una sorta di prosieguo della Scolastica in cui il quadro di riferimento fisico-cosmologico è cambiato ma si ritorna a trovare la sistemazione di Dio dovunque nel nuovo mondo. Si noterà che Galileo non c’è più. Che si polemizza con Descartes ma metafisicamente. L’argomento del contendere con Descartes è se si conserva la forza o la quantità di moto. Per il resto l’onnipresenza di Dio è la medesima. Oltre a Galileo si vede quanto è distante anche Huygens e vedremo quanto lo sarà Newton, anche se non riuscirà a sbarazzarsi di Dio ma neppure di magie ed alchimie. E’ stata molto dura uscire dal pantano dei secoli passati e bisognerà avere ancora un poco di pazienza per riuscire a risolvere la gran parte dei problemi con l’Illuminismo che aprendo la strada alla ragione metterà al bando ogni superstizione.

        Vediamo allora di capire qual è il contributo netto di Leibniz alla fisica⁽⁶⁾ che, come diceva,  non può essere considerata solo meccanica e quest’ultima non può essere solo cinematica. Questo è un punto di chiara polemica con Descartes sostenuto già a partire dall’Hypothesis physicae nova del 1671. Leibniz riteneva infatti che voler solo descrivere cinematicamente i fenomeni naturali è troppo limitativo e che sarebbe stato necessario aggiungere anche una trattazione di tipo dinamico poiché la materia, nella sua essenza, non può solo essere estensione e movimento. Intanto sembra evidente che egli fosse completamente insoddisfatto del meccanicismo di Descartes e, a maggior ragione lo fu di quello newtoniano subito dopo averlo conosciuto attraverso i Principia che egli lesse in prima edizione nel 1689 (due anni dopo la pubblicazione). Particolarmente la forza newtoniana che agiva senza intermediari e l’intera concezione del mondo di Newton lo trovarono profondamente contrariato ed egli tentò di costruire un qualcosa di alternativo alla strada che Newton aveva imboccato e che Leibniz giudicava lastricata di metafisica, ma riuscì a costruire ben poco ed infatti per quanto si vogliano mettere insieme contributi e per quanto si vogliano leggere con il metodo storico-critico, è proprio l’altra metafisica che egli proponeva a non permettergli di andare oltre alcune pur interessanti enunciazioni che però vedevano solo dimostrazioni geometriche e mai un uso dell’esperienza metodico come iniziato da Galileo e realizzato da Huygens e Newton. L’importanza della fisica di Leibniz risulta addirittura di un livello inferiore a quello di Descartes anche se, ripeto, egli ebbe delle intuizioni molto brillanti alla base davvero, se sviluppate ed integrate opportunamente, di una meccanica esterna a quella newtoniana. Mi riferisco al suo insistere sul concetto di forza che, nel nostro linguaggio è energia, che egli considera nella sua versione cinetica⁽⁷) e forse anche nella sua forma potenziale quando egli parla di forza morta. A lato di ciò vi è certamente un altro proficuo insistere, quello sull’impossibilità del moto perpetuo (anche qui distinto in due, il meccanico ed il fisico)  che, per ora, è solo moto perpetuo di 1ª specie (sull’argomento avevano dato già dei contributi Stevin, Galileo, Huygens e lo stava dando J. Bernouilli⁽⁸⁾ (usava dire Leibniz che solo accettando la sua misura della forza era esclusa la possibilità di un perpetuum mobile). E non è poco se ancora sul finire del Settecento ai molti che si affannavano con mirabolanti invenzioni l’Accademia Reale delle Scienze di Francia dovette dire basta per non essere sommersa da progetti di macchine miracolose. La stessa Accademia divulgò nel 1775 il seguente testo: La costruzione di una macchina del moto perpetuo è assolutamente impossibile. Anche ammesso che l’attrito e la resistenza del mezzo non distruggessero infine l’effetto della potenza motrice primaria, tale potenza non potrebbe produrre un effetto uguale alla sua causa. Se le intuizioni di Leibniz avessero avuto una qualche intersezione con alcuni lavori che aveva fatto Huygens (macchina a polvere da sparo) e con altri che faceva Papin (la sua pentola) il concetto di conservazione dell’energia su cui insisteva Leibniz avrebbe avuto una ricaduta maggiore ma sarebbe comunque mancata la richiesta sociale di rendimento legata a combustibili che dovevano arrivare a servire massicciamente per imporre il problema.

        Per Leibniz l’universo, in cui non è ammesso alcun vuoto, è costituito, come visto, da monadi, assimilabili a punti matematici dotati di forza ma non di materia (ho già accennato che da qui parte quella corrente di pensiero che prende il nome di dinamismo e che avrà come seguaci Boscovich, Schelling, Faraday, …). Leibniz aveva serie obiezioni contro chi sosteneva un mondo costituito da atomi e vuoto. La materia non può essere costituita da atomi duri, estesi, indivisibili perché ciò comporterebbe  una discontinuità di fondo che egli non può accettare per il principio di ragion sufficiente⁽⁹⁾ che egli enuncerà chiaramente nella sua Monadologie secondo il quale non si capisce bene qual è il punto in cui il processo di suddivisione della materia deve aver termine per disporre di un atomo. Inoltre, se tutte le sostanze fossero costituite da atomi dotati di estensione, non si capisce di quale sostanza dovrebbero essere costituiti gli atomi. Infine se gli atomi sono, come ipotizzato, perfettamente rigidi, la teoria degli urti di corpi perfettamente rigidi avrebbe dei problemi. Ed anche il concetto di massa sfugge a Leibniz o meglio gli è presente come resistenza al cambiamento di moto e, per questo, deve essere per lui una forma di potenza, un’entità dinamica ed anch’essa quindi riportabile alla sua forza. La forza a cui si riferisce Leibniz inizia con le caratteristiche spirituali e diventa poi quella che si considera in meccanica. Come in una progressione aritmetica ogni termine risulta individuato dal precedente e dalla legge che regola la progressione medesima, così come ogni successivo istante nell’infinito divenire di questo universo di monadi, è contenuto nel presente governato da una legge logico-matematica superiore (in modo analogo ma con finalità opposte, si espresse Laplace un centinaio di anni dopo). Ed il tempo delle monadi non ha una gerarchia prima-dopo ma ogni istante è uguale ad un altro. Conseguenza di ciò è che non ha senso di parlare di causa (il prima) ed effetto (il dopo)⁽¹⁰) che vengono bollate, nell’Essays come concetti a priori. E, in una catena logica conseguenziale, la forza viva si conserva. E’ evidente che in tale concezione l’esistenza di uno spazio assoluto, come pensato da Newton, è inammissibile. Spazi e tempi regolano quelle monadi per le quali non esiste la causa che precede l’effetto e quindi spazio e tempo non possono che essere coesistenze e quindi concetti solo relativi. A questo proposito Jammer [bibl. 23] osserva: “Furono la relatività dello spazio e l’assolutezza del moto a condurre Leibniz all’esistenza della forza, contrariamente a Newton per il quale l’assolutezza della forza provava l’assolutezza del moto e di conseguenza, l’assolutezza dello spazio”.

        Ma, come accennato, la critica di Leibniz a Newton era radicale, molto più complessa e generale di quanto qui accennato. Dopo aver affermato che “nel mondo persiste sempre la stessa forza⁽¹¹⁾ e la stessa, energia, che solo passa, di materia in materia, conformemente alle leggi della natura” e che quindi, è illusorio pensare ad un Dio che interviene sempre nell’universo come un orologiaio che continuamente mette a punto il suo orologio, Leibniz passa a rigettare l’idea di uno spazio assoluto indipendente dai corpi in esso contenuti poiché sono proprio questi ultimi ad individuare, con il loro ordine, lo spazio; e quest’ultimo, lungi dall’essere assoluto, è meramente relativo, come il moto⁽¹²⁾; esso non avrebbe ragione di esistere se non vi fossero corpi in un certo ordine [qui si reclama il principio di ragion sufficiente secondo il quale “nulla avviene senza ragion sufficiente; cioè, nulla avviene senza che, chi conosce le cose, abbia possibilità di indicare una ragione che basti a determinare perché le cose siano così e non altrimenti”]. Leibniz prosegue affermando l’impossibilità di esistenza del vuoto e quindi di corpuscoli indivisibili (atomi). È ancora il principio di ragion sufficiente che lo porta a questa conclusione, poiché:

Non v’è ragione plausibile che possa limitare la quantità di materia. Perciò tale limitazione non può aver luogo … dunque tutto è pieno. Lo stesso ragionamento prova che non v’è corpuscolo che non possa essere suddiviso.

inoltre Dio può agire solo sulla materia e quindi in nessun modo può ammettersi spazio vuoto.

    E poi, che assurdità lo spazio assoluto indipendente dalla materia ! La sua ammissione comporterebbe l’esistenza di spazio anche quando non vi fosse materia.

Cosi la finzione di un universo materiale finito che va passeggiando tutt’ intero in uno spazio vuoto infinito non può essere ammessa … Infatti, oltre che non v’è spazio reale fuori dell’universo materiale, una tale ragione sarebbe senza scopo; sarebbe un lavorare senza far nulla, agendo nihil agere non si produrrebbe alcun mutamento osservabile da chicchessia. Ed il movimento è indipendente dall’osservazione, ma non è indipendente dalla osservabilità. Non v’è movimento quando non v’è cangiamento osservabile. Anzi, quando non v’è cangiamento osservabile non c’è cangiamento affatto.

      Al di là delle singole argomentazioni, vi è una critica a quella che viene chiamata azione a distanza. Nella legge di gravitazione universale si dice che: due corpi di massa m₁ ed m₂ si attraggono reciprocamente con una forza F che è proporzionale, secondo una costante G, al prodotto delle masse dei due corpi ed inversamente proporzionale al quadrato della distanza Rche, appunto, separa i due corpi. Fin qui quello che nella formula è scritto. Per cogliere il senso delle critiche di Huygens e Leibniz è interessante andare a vedere cosa non è scritto in questa relazione. L’azione F si esercita tra m₁ ed m₂ lungo la congiungente i centri delle due masse; si tratta quindi di un’azione rettilinea. Inoltre essa è istantanea e a distanza nel senso che non si richiede tempo (che appunto nella relazione non compare direttamente) affinché due masse si accorgano l’una dell’altra (si noti che questo tipo di azione tra massa e massa senza alcun intermediario era ostica allo stesso Newton). Per spiegarci meglio, supponiamo che nell’universo vi sia una sola massa m₁. Ebbene, se prendiamo in considerazione una seconda massa m₂, in questo universo, ambedue le masse cominceranno ad attrarsi reciprocamente all’istante. Questo fatto comporta una conseguenza importantissima: l’esigenza di azioni istantanee implica che ci siano delle entità dotate di una velocità infinita. E tutto questo aprirà a controversie incredibili che convergeranno in importantissimi sviluppi, con la nascita della teoria di campo, con l’affermazione cioè dell’azione a contatto ad opera particolarmente di Faraday, per arrivare ancora ad Einstein.

        A questo punto c’è da osservare che uno dei limiti allo sviluppo dei concetti che elaborava Leibniz era la loro trattazione fatta ancora in termini geometrici. Con il calcolo infinitesimale che lo stesso Leibniz aveva inventato si sarebbero potuti fare giganteschi passi avanti. Ma mai Leibniz utilizzò la sua invenzione in questioni di meccanica⁽¹³⁾.

3 – CONCLUSIONE

        Solo alcune note di commento a quanto scritto.

        Leibniz fu un personaggio multiforme, impegnato in molteplici campi d’interesse. Fu diplomatico, storico, metafisico, filosofo, logico, matematico, fisico, biologo, geologo, paleontologo, sociologo, psicologo, tecnologo, …. E probabilmente proprio per questo suo eclettismo non riuscì in vari ambiti a dare il meglio di sé. E’ certo che ebbe intuizioni importanti ma rimasero lì, senza ulteriori studi ed approfondimenti. Come ha osservato Russell, vi sono almeno due Leibniz, quello che conosciamo dalle cose pubblicate e quello che stiamo ancora conoscendo dalle sue cose inedite. Non sappiamo se le cose inedite lo sono state per espressa volontà dell’autore, come sembra credere Russell, o se per mancanza di tempo (riordinare, sistemare, rendere leggibile, …) dell’autore. In ogni caso restiamo nel dubbio.

        I suoi contributi alla matematica, e particolarmente al calcolo (ma anche precursore dell’algebra di Boole e della logica simbolica), furono fondamentali per l’uso immediato che ne seguì e dal quale poterono sviluppare molte branche della scienza.  Non altrettanto fondamentali furono i suoi contributi alla fisica. Ricordiamo la conservazione della forza viva che sarà alla base del dibattito per molti anni e che aprirà alla conservazione dell’energia. Ricordiamo il suo dinamismo, che soprattutto nell’Ottocento avrà importanti ricadute. Ricordiamo infine la sua critica al mondo meccanico di Descartes e Newton che terrà aperto un canale alternativo a questa fisica. Ed in mezzo a tanti meriti non si può sottacere una metafisica asfissiante non dissimile da quella di Descartes che fa piombare Leibniz in un mondo antico, aristotelico, che non ha capito la lezione di Galileo e di Huygens.

NOTE

(1) Leibniz riservò a Descartes dei giudizi estremamente pesanti. Scrisse:

E’ certo, indubbiamente, che Descartes si è servito di artifici per trarre profitto da scoperte altrui …

E’ stato necessario, per il progresso delle scienze, disingannare coloro che avevano creduto bastasse il suo metodo …

(2) Nella Biblioteca di Hannover il conte Foucher de Careil scoprì intorno alla metà dell’Ottocento i documenti che erano in possesso di Leibniz e che la commissione della Royal Society non prese mai in considerazione. Con tale documentazione a disposizione, nel 1856, due giudici come Biot e Lefort, scrissero un nuovo Commercium epistolicum nel quale si dicono molte cose assolutamente condivisibili. Intanto che nella commissione inglese vi era un solo geometra in grado di comprendere il problema, che alcuni dei commissari non avevano firmato la relazione finale e che la relazione finale fu manipolata nelle sue edizioni successive, quindi che con i nuovi documenti a disposizione si può solo dire che il calcolo infinitesimale è un tipico esempio di scoperta simultanea ed indipendente, tra l’altro documentata dalla diversità dei metodi e del simbolismo.

Oggi vi è un totale accordo di tutti gli studiosi sulla priorità di Leibniz nel metodo di calcolo che più ha influenzato gli ulteriori sviluppi dell’analisi, metodo che, ancora oggi, per la semplice simbologia, è utilizzato.

(3) Leibniz, al pari di Descartes ed in parte Newton, non riesce a separare la sua fisica dalla metafisica. Anche per lui Dio è l’artefice di tutte le cose e addirittura si lamenterà di Newton con la principessa Carolina di Galles, affermando che quanto era sostenuto nei Principia e nell’Opticks minava le basi della religione. Newton permise allora al suo fervente ammiratore, il teologo Samuel Clarke, di difenderlo con lettere da inviare a Leibniz e quindi pubblicare (la pubblicazione di tale corrispondenza avvenne nel 1717, un anno dopo la scomparsa di Leibniz). In tale controversia epistolare Clarke-Leibniz, iniziata nel 1712, venivano dibattute le implicazioni religiose della filosofia meccanica. Ambedue i contendenti vedevano l’universo come se fosse un orologio. Clarke, sulle orme di Newton sosteneva che questo orologio aveva un continuo bisogno dell’assistenza di Dio e quest’affermazione aveva una piccola storia. Dopo la prima edizione dei Principia Newton era stato accusato di ateismo perché Dio non compariva nella sua opera. La cosa spaventò Newton che in nessun caso si sentiva ateo. Rimediò nella seconda edizione dei Principia quando aggiunse un capitolo in chiusura dell’opera, lo Scolio generale. In tale capitolo si sosteneva che era Dio che riforniva continuamente il mondo di energia e, se per caso qualche pianeta avesse avuto qualche problema, Dio sarebbe intervenuto con una spintarella a rimetterlo in orbita. Inoltre egli parla esplicitamente di spazio fisico come sensosrium dei. E queste ultime posizioni vengono richiamate da Clarke nelle sue lettere a Leibniz. All’orologio di Clarke-Newton rispondeva Leibniz che tale posizione significava un ribassare la perfezione di Dio ed argomentava che Dio avrebbe dovuto essere un orologiaio perfetto, previdente di tutto ed in grado di rimediare ad ogni problema relativo all’armonia e alla bellezza prestabilite. Ambedue sostenevano comunque la provvidenza divina in un mondo meccanicista che, rispetto a quello di Aristotele, relegava i teologi ad un posto più defilato, poiché ora le finalità scomparivano. E’ il primo sintomo dell’impatto della rivoluzione scientifica sul mondo cristiano, impatto che ben presto diventerà distruttivo per i filosofi cristiani.

Si vanno delineando i caratteri dell’Illuminismo anticipato dal Dizionario storico e critico (1695-1697) di Pierre Bayle (1647-1706), che ha come scopo la divulgazione della cultura. Tra le altre cose Bayle riconosce l’esistenza del male (fatto incompatibile per i cristiani che avevano condannato il manicheismo) ed afferma con forza che fede e ragione sono tra loro inconciliabili e chi ha la ragione non deve temere nulla in quanto l’ateo, non meno del credente, può avere una vita morale piena. Queste posizioni eccitarono i bigotti come Leibniz che si sentì spinto immediatamente a scrivere, nella Teodicea (una sorta di conquista della metafisica attraverso la ragione) che sto discutendo, che questo è il migliore dei mondi possibili. Dio, che ha creato tutto, non può averlo fatto in modo imperfetto. Anche il male quindi fa parte di un disegno complessivo dell’armonia dell’esistente (il male non è creazione di Dio, ma qualcosa che è da Lui permesso, in quanto un mondo perfetto e privo di male non sarebbe stato veramente un mondo, ma una reduplicazione di Dio. In accordo con Paolo di Tarso ed Agostino, Dio ha permesso il male per ricavarne un bene maggiore). I contemporanei risero molto di tale posizione e Voltaire creò un personaggio ridicolo (Pangloss = tutte le lingue, con riferimento ai suoi tentativi incompiuti di creare un linguaggio universale), che rappresentava Leibniz, nel suo Candide. Dice Voltaire che Pangloss insegnava la metafisico-teologo-cosmologo-scempiologia. Più recentemente, all’affermazione che questo è il migliore dei mondi possibili, Bradley aggiungerà che quindi in esso necessariamente tutto è male.

(4) Bertrand Russell, avendo osservato che Leibniz lasciò inedita una massa notevolissima dei suoi lavori nei quali si esprimevano idee non ortodosse che rappresentavano il suo pensiero più profondo e che gli avrebbero provocato riprovazione ed ostilità generale, accusò Leibniz di doppiezza con queste parole:

Leibniz fu uno dei più alti intellettuali di tutti i tempi, ma umanamente non fu molto ammirevole. Aveva, è vero, quella virtù che sarebbe desiderabile trovare nell’attestato di un impiegato di concetto: laborioso, frugale, temperante ed onesto; ma era del tutto privo di quelle più alte virtù filosofiche così notevoli in Spinoza. I suoi più profondi pensieri non erano tali da guadagnargli la popolarità e per questo lasciò le sue note inedite nella scrivania. Quello che pubblicò, invece, era destinato a ricevere l’approvazione dei principi e delle principesse. Di conseguenza ci sono due sistemi filosofici che si possono attribuire a Leibniz: uno, quello che egli stesso diffuse, era ottimista, ortodosso, fantastico e frivolo; l’altro, che recentemente è stato portato alla luce dagli editori, era profondo, coerente, molto spinoziano e sorprendentemente logico [Da Russell, Storia della filosofia occidentale, Vol III, pag. 761

(5) Un articolo in francese che tratta anche della quadratura di Pascal della cicloide (o roulette) si può leggere qui. Un lavoro più completo ed elaborato sulle quadrature di Pascal (Claude Merker – Le chant du cygne des indivisibles: le calcul intégral dans la dernière oeuvre scientifique de Pascal) sempre in francese, si può leggere qui.

(6) Gli scritti di meccanica di Leibniz comprendono numerosi scritti brevi, in lingua tedesca, latina, francese; quindi altri lavori in cui spesso è difficile separare il contributo fisico da quello metafisico ed altri ancora che ripetono gli stessi concetti più e più volte. Elenco di seguito alcuni di tali lavori, riportando in grassetto quelli più significativi:

Hypothesis Physica Nova 1671

Brevis demonstratio erroris memorabilis Cartesii 1686

Dynamica de potentia et Legibus Naturae corporeae o Tentamen scientiae novae scritta a partire dal 1689 durante il viaggio in Italia e rimasta inedita

De causa gravitatis, et defensio sententiae auctoris de veris naturae legibus contra Cartesianos 1690

Lettre sur la question, si l’essence du corps consiste dans l’etendue  1691

Regle generale sur la composition des mouvemens 1692

Essay de dynamique scritto nel 1692 ma pubblicato solo nel 1859

De primae philosophiae Emendatione et de Notione Substantiae 1694

Specimen dynamicum 1695

Vi è poi il lavoro di ottica:

Unicum opticae, catoptricae et dioptricae principium 1682.

(7) A questo proposito dice Westfall:

La forza viva (vis viva) rappresentava per Leibniz molto di più di un semplice numero. Essenza dell’essere stesso, la forza viva era gravida di significato metafisico, con implicazioni che andavano ben oltre il regno della meccanica. La conservazione della vis viva era per Leibniz equivalente all’eternità della creazione di Dio. All’interno della meccanica, forniva intuizioni su numerosi problemi. Il primo naturalmente era l’aumento della forza nel moto uniformemente accelerato, il problema che usò per dimostrare l’errore di Cartesio. Il secondo era l’urto, in cui si basò sull’analisi di Huygens ma andando oltre. L’elasticità costituì sempre un problema per Huygens, che affrontò il caso ideale, l’urto di due corpi perfettamente duri. In tale caso, l’urto era istantaneo ed il moto originale continuava nella direzione opposta. Leibniz affrontò il problema della dinamica dell’urto elastico, sostenendo che la vis viva del corpo in moto si trasformava in forza elastica quando il corpo perveniva ad uno stato di quiete e rinasceva dalla forza elastica quando si produceva un moto nuovo nella direzione opposta. Leibniz ampliò la sua analisi fino ad includere l’urto anelastico. Quando due pezzi uguali di argilla molle che si muovono con uguali velocità in direzioni opposte si scontrano, entrambi si fermano. Cosa accade alla forza viva in tal caso? Leibniz concordava sul fatto che i pezzi d’argilla in quanto tali perdevano la loro forza viva. Ma questa perdita della forza totale non contraddice la verità inviolabile della legge della conservazione della stessa forza nel mondo. Infatti ciò che è assorbito dalle parti minute non è affatto perduto per l’universo, anche se lo è per la forza totale dei corpi convergenti.

Il suggerimento che la forza persa dai grandi corpi venga trasferita alle loro parti era gravido di significato per il futuro. Leibniz in realtà lo enunciò aprioristicamente per salvare il principio della conservazione della forza viva. Non comprese che la forza delle parti (diciamo il loro moto) può essere misurata come calore.

Con Leibniz, il tentativo deliberato di Huygens di limitare la meccanica alla cinematica, di discutere i moti senza fare riferimento alla forza, fu abbandonato; egli coniò il termine «dinamica» per definire una meccanica basata sul concetto di forza. Questo suo concetto, però, era diverso da quello impiegato nella fisica moderna, che segue Newton. La «forza», cosi come Leibniz usava la parola, può essere tradotta nei nostri termini in «energia cinetica». Per quanto la sua filosofia fosse diversa da quella cartesiana, accettava ancora la premessa che la forza non è qualcosa che agisce sui corpi per cambiarne il moto, ma qualcosa che i corpi hanno. Con la sua idea di forza morta, Leibniz si accostava all’altra concezione, ma la limitava a situazioni statiche. Pur paragonando la forza elastica alla gravità, come una forza morta da cui può emergere una forza viva, non spinse mai la sua analisi al di là delle semplici parole.

(8)  Il concetto di conservazione sarà invece assente nella fisica newtoniana (in ogni urto e in ogni moto, per Newton, c’è una parte di movimento che va perduta allo stesso modo in cui si perde movimento nel moto degli astri. È l’opera di Dio che rifornisce il mondo, istante per istante, di ciò di cui continuamente viene privato).

(9) Nella Proposizione 32 della Monadologie, Leibniz afferma:

I nostri ragionamenti si basano sul … Principio di ragion sufficiente, in virtù del quale consideriamo che non si potrebbe trovare nessun fatto vero o esistente, né nessuna enunciazione vera, senza che vi sia una ragione sufficiente perché sia così e non in altra maniera. Anche se la maggior parte di tali ragioni non possano essere conosciute da noi.

(10) Quanto qui sostenuto è ciò che continuamente afferma Leibniz. Anche se, nell’Essay de dynamique afferma (Definizione 3, Assioma 1) quanto segue:

Si conserva la stessa quantità di forza, o meglio l’intero effetto è uguale alla causa totale.

(11) C’è da aggiungere per pura curiosità che Leibniz introdusse anche un’altra grandezza, l’azione motrice, definita come il prodotto mvs (massa per velocità per spazio percorso). Essa avrebbe dovuto sostituire la quantità di moto mv nel caso di moto uniforme.

(12) Franco Voltaggio [bibl. 1] discute egregiamente dal punto di vista filosofico la teoria del moto di Leibniz (pagg. 151-160).

(13) Un articolo in francese che tratta della Fisica nei lavori di Leibniz, si può leggere qui.

BIBLIOGRAFIA

(1)  F. Voltaggio – Leibniz – Ubaldini 1971

(2)  Cecchi,V. Mathieu, Ravera – Leibniz – Laterza 1976, 1988, 1991

(3)  Luis Figuier – La ciencia y sus hombres – D. Jaime Seix, Barcelona 1881

(4)  B. Russel – Storia della filosofia occidentale – Longanesi 1967

(5)  Leibniz Newton – La disputa sull’analisi – Boringhieri 1958

(6)  Leibniz – Nuevos ensayos sobre el entindimiento humano – Editora nacional, Madrid 1977

(7)  Leibniz – Discurso de metafisica – Alianza Editorial, Madrid 1981

(8)  Leibniz – Filosofia para princesas – Alianza Editorial, Madrid 1989

(9)  Leibniz – Monadologia – Orbis, Barcelona 1983

(10) Leibniz – Profesión de fe del filósofo – Orbis, Barcelona 1983

(11) Leibniz – Análisis infinitesimal – Tecnos, Madrid 1994

(12) Leibniz – Escritos de dinámica – Tecnos, Madrid 1991

(13) A. J. Durán – Historia, con personajes, de los conceptos del cálculo – Alianza Universidad 1996

(14) Abbagnano (a cura di) – Storia della filosofia – UTET 1998

(15) Carl B. Boyer – Storia della matematica – Mondadori 1990

(16) Carl B. Boyer – Storia del calcolo – Bruno Mondadori 2007

(17) A. Perez de Laborda – Leibniz e Newton – Jaca Book 1986

(18) Morris Kline – Matematical thought from ancient to modern times – Oxford University Press, 1972

(19) Alexander Koiré – Studi newtoniani – Einaudi 1972

(20) Ernst Mach – La meccanica nel suo sviluppo storico-critico – Boringhieri 1968

(21) Paolo Rossi – La nascita della scienza moderna in Europa – Laterza 2000

(22) Richard S. Westfall – La rivoluzione scientifica del XVII secolo – il Mulino 1984

(23) Max Jammer – Storia del concetto di forza – Feltrinelli 1971

(24) Mary B. Hesse – Forze e campi – Feltrinelli 1974

(25) A. Rupert Hall – Da Galileo a Newton – Feltrinelli 1973

(26) Max Jammer – Storia del concetto di massa – Feltrinelli 1974

(27) Guido Castelnuovo – Le origini del calcolo infinitesimale nell’era moderna – Feltrinelli 1962

(28) U. Forti – Storia della scienza – Dall’Oglio 1968

(29) R. Tatón (coordinata da) – Storia generale delle scienze – Casini 1964

(30) Nicola Abbagnano (coordinata da) – Storia delle scienze – UTET 1965

(31) Paolo Rossi (diretta da) – Storia della scienza – UTET 1988

http://www.filosofico.net/leibniz1.htm

Categorie:Senza categoria