Ingegneria Meccanica – Roma Tre

AA/2011-2012

APPUNTI PER IL CORSO

(Ripresi integralmente e da me assemblati dai testi di bibliografia)

Roberto Renzetti

Bibliografia: R. Renzetti –Vari appunti miei raccolti negli anni -www.fisicamente.blog

2 – SULL’ELETTRODINAMICA DEI CORPI IN MOVIMENTO (1905)

    I due lavori di Einstein, sul moto browniano e sui quanti di luce furono presentati alla rivista Annalen der Physik tra il marzo ed il maggio 1905. Il 30 giugno dello stesso anno un nuovo lavoro doveva aggiungersi ai precedenti: Sull'elettrodinamica dei corpi in movimento (826) E' questo l'articolo nel quale Einstein introduce la  relatività. Ad esso se ne aggiungerà ancora un altro, "interessante conseguenza [dei] risultati della precedente ricerca", nel settembre dello stesso anno: L'inerzia di un corpo è dipendente dal suo contenuto di energia? (827)   In questo lavoro, come elaborazione di quanto ottenuto nel precedente articolo, viene data una prima formulazione del principio di equivalenza tra massa ed energia. (828)
    Cominciamo con il discutere Sull'elettrodinamica dei corpi in movimento.  
    La prima cosa che va ricordata è che Einstein non conosceva il lavoro di Lorentz del 1904 (si veda la nota 781 bis); occorre però aggiungere che se anche Einstein fosse stato a conoscenza di questo lavoro, nulla sarebbe cambiato nel giudizio di svolta radicale che il suo articolo ha rappresentato.
    Certamente poi non conosceva gli articoli di Poincaré sull'argomento , del 1905-1906 (essi erano stati inviati alle riviste contemporaneamente al suo).
     Infine egli non aveva che una conoscenza indiretta dell'esperienza di Michelson e Morley (attraverso i lavori di Lorentz del 1892 e 1895); ma anche qui vale il giudizio dato precedentemente per Lorentz: anche se avesse conosciuto questa esperienza nei dettagli non sarebbe cambiato nulla rispetto al suo approccio assolutamente originale e per la verità molto ardito.   (829)   
    Occorre poi sottolineare che l'articolo di cui si parla, e che comunemente va sotto il nome di articolo sulla relatività, è in realtà un articolo "sull'elettrodinamica dei corpi in movimento" nel quale si tenta un approccio radicalmente divergo ai problemi dell'elettrodinamica così come si ponevano nell'ultimo articolo di Lorentz sull'argomento (1895) conosciuto da Einstein. Come si ricorderà in quel lavoro ancora ci si muoveva al primo ordine di v/c e si cercava una soluzione del secondo ordine. La diversità radi cale della trattazione einsteniana sta nel tentativo (riuscito) di risolvere le questioni che si ponevano mediante la fisica dei principi. Egli infatti non entra in estenuanti e successive elaborazioni elettrodinamiche; non fa una fisica costruttiva tentando di "formare un quadro dei fenomeni complessi partendo da certi principi relativamente semplici", da elementi ipotetici, in definitiva, di tipo riduzionista. Einstein cerca invece delle"proprietà generali dei fenomeni osservate empiricamente, principi dai quali vengono dedotte formule matematiche di tipo tale da valere in ogni caso particolare si presenti". Come più volte ricordato, è lo stesso tipo di approccio che egli ha seguito nei suoi due lavori precedenti del 1905.
    Il problema principale per Einstein è la sua profonda insoddisfazione per le equazioni di Maxwell-Lorentz. (830)    Egli aveva provato più volte a correggerne gli errori mediante un approccio costruttivo, ma, come già detto, tutti i tentativi "fallirono completamente". Nel caso particolare dell'elettrodinamica, quelle equazioni fornivano, come vedremo, risultati diversi se applicate a sistemi di riferimento diversi. (831) Inoltre, anche qui come nel caso dei quanti di luce, l'asimmetria esistente tra campi continui e cariche discrete è un prodotto della teoria degli elettroni che Einstein non si sente di accettare. Dice Einstein nelle Note autobiografiche:  (832)

“Se si considera … la teoria, si resta colpiti dal dualismo insito nel fatto che il punto materiale in senso newtoniano ed il campo come continuo fisico stiano l’uno accanto all’altro come concetti elementari. L’energia cinetica e l’energia di campo appaiono sostanzialmente diverse. La cosa risulta tanto più insoddisfacente in quanto, secondo la teoria di Maxwell, il campo magnetico di una carica elettrica in movimento rappresenta l’inerzia. Ma allora, perché non tutta l’inerzia ? In questo caso rimarrebbe solo l’energia di campo, e la particella sarebbe semplicemente una zona di densità particolarmente elevata dell’energia di campo … ed il fastidioso dualismo sarebbe eliminato.”
Infine non va dimenticato che le elaborazioni di Lorentz introducevano qua e là delle profonde modificazioni ai concetti fondamentali della meccanica. Ed allora, dato che si procedeva in silenzio ad una revisione della meccanica, perché non pagare questo prezzo ma al fine di ottenere dei principi più generali, magari andando ad una revisione più profonda della meccanica stessa ? (833)
Ma, a detta dello stesso Einstein, ciò che lo colpiva di più era proprio l’asimmetria che si presentava quando si applicavano le equazioni di Maxwell a differenti sistemi di riferimento. Abbiamo già detto che più volte Einstein provò a modificare le equazioni di Maxwell-Lorentz. Egli tentava cioè di far rientrare la suddetta asimmetria cercando un apparato teorico, sia per i fenomeni ottici che per quelli elettromagnetici, nel quale solo avesse significato il moto relativo, un apparato teorico cioè che mantenesse immutate le equazioni nel passaggio da un riferimento ad un altro che fosse in moto traslatorio uniforme rispetto al primo. Nel portare avanti queste elaborazioni egli sempre più si era convinto che “né la meccanica, né la termodinamica potevano pretendere ad una validità assoluta”. Lo stesso Einstein ci dice che a poco a poco cominciò a “disperare della possibilità di scoprire le vere leggi attraverso tentativi basati su fatti noti”. Gli servivano dei principi -universali sull’esempio di quelli che governavano la termodinamica. Dove e come trovarli ? Dice Einstein nelle Note autobiografiche: (834)
“Dopo dieci anni di riflessione, un siffatto principio risultò da un paradosso nel quale mi ero imbattuto all’età di 16 anni; se io potessi seguire un raggio di luce a velocità c (la velocità della luce nel vuoto), il raggio di luce mi apparirebbe come un campo elettromagnetico oscillante nello spazio, in stato di quiete. Ma nulla del genere sembra sussistere sulla base dell’esperienza o delle equazioni di Maxwell. Fin dal principio mi sembrò intuitivamente chiaro che, dal punto di vista di un tale ipotetico osservatore, tutto debba accadere secondo le stesse leggi che valgono per un osservatore fermo rispetto alla Terra. Altrimenti, come farebbe il primo osservatore a sapere, cioè come potrebbe stabilire, di essere in uno stato di rapidissimo moto uniforme ?”
Che significa il paradosso di Einstein ?
Se uno si muovesse alla velocità della luce, con un’ onda elettromagnetica, dovrebbe descrivere il mondo in un modo differente da chi è in riposo rispetto alla Terra, egli, vedendo solo l’oscillazione di un campo che non si propaga nel tempo, sarebbe in grado di decidere qual è il suo stato di moto rispetto all’etere (si sta muovendo con velocità c) violando in questo modo il principio classico di relatività; inoltre questo fatto non è previsto all’interno delle stesse equazioni di Maxwell. (835) E’ come se si avesse a che fare con la luce immobile e ciò è inammissibile poiché la stessa luce è definita proprio dalla sua frequenza di movimento. Insomma, come molto bene dicono Schwartz e Mc Guinnes, (836) se uno camminasse alla velocità della luce, non vedendo la propria immagine riflessa in uno specchio (che la sua mano sostiene davanti al viso), sarebbe in grado di capire che cammina alla velocità della luce senza bisogno di guardar fuori; e ciò è negato dal principio classico di relatività di Galileo.
A questo punto però conviene andare con ordine, prendendo l’articolo di Einstein e seguendolo passo passo.
L’introduzione del lavoro contiene già tutti gli elementi che abbiamo discusso.

INTRODUZIONE
L’articolo inizia così: (837)
“E’ noto che l’elettrodinamica di Maxwell – come essa attualmente viene d’ordinario concepita – conduce nelle sue applicazioni a corpi in movimento ad asimmetrie che paiono non essere aderenti ai fenomeni.”
Ecco dunque che il primo motivo è l’insoddisfazione per la teoria di Maxwell, negli ultimi sviluppi di Lorentz, ed in particolare perché questa teoria origina delle asimmetrie. Di quali asimmetrie si tratta ?
Einstein non ricorre ad esemplificazioni sofisticate ma al più semplice dei fenomeni elettrodinamici, che risale a Faraday; il movimento relativo di un magnete e di un conduttore e le azioni elettrodinamiche che si producono tra questi due oggetti. Lo stesso Einstein dice:
“Si pensi ad esempio alle interazioni elettrodinamiche tra un magnete ed un conduttore. Il fenomeno osservabile dipende qui solo dal moto relativo fra magnete e conduttore, mentre secondo il consueto modo di vedere sono da tener rigorosamente distinti i due casi che l’uno o l’altro di questi corpi sia quello mosso. Infatti, se si muove il magnete e rimane fisso il conduttore, si produce nell’intorno del magnete un campo elettrico di certi valori di energia il quale provoca una corrente nei luoghi ove si trovano parti del conduttore. Rimane invece fisso il magnete e si muove il conduttore, non si produce nell’intorno del magnete alcun campo elettrico, ma al contrario [si produce] nel conduttore una forza elettromotrice, alla quale non corrisponde per sé alcuna energia, ma che – supposta l’uguaglianza del moto relativo nei due casi considerati – dà occasione al prodursi di correnti elettriche della stessa grandezza e dello stesso percorso, come nel primo caso [avevano dato] le forze elettriche.”
Dicevamo che questa esemplificazione è semplice ma non altrettanto la sua interpretazione teorica, soprattutto in relazione all’asimmetria che essa comporta e di cui parla Einstein. Per cogliere il nocciolo del ragionamento, serviamoci della figura 41. (838) Innanzitutto osserviamo che da sfondo alle due situazioni, nella teoria cui fa riferimento Einstein

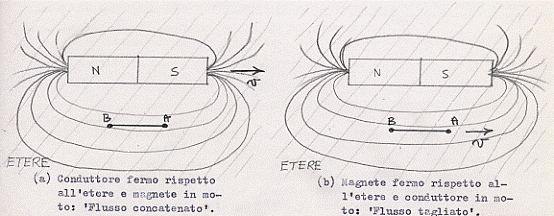
Figura 41

ed in particolare nella teoria di Lorentz, c’è un etere immobile che funge da sistema a cui riferire i singoli moti. Per cui nel primo caso preso in considerazione (figura 41a) il conduttore risulta fermo rispetto all’etere mentre il magnete si muove con velocità v, sempre rispetto all’etere. Nel secondo caso (figura 41b) le situazioni, ancora rispetto all’etere, sono invertite. Facendo riferimento alle equazioni di Maxwell, nel primo caso, quando il magnete si sposta, origina una variazione dell’induzione magnetica B in tutto l’etere che circonda il magnete e nel conduttore. Poiché varia B nell’etere, varia il flusso di B concatenato con il conduttore. Ricordando la terza delle equazioni di Maxwell (la 7 del paragrafo 5 del capitolo 3) ad una variazione del flusso di B si accompagna un campo elettrico nell’etere che circonda il magnete. Le cariche (gli elettroni), in quiete nel conduttore, sono soggette alla forza originata dal campo elettrico (mentre non sentono alcuna forza magnetica poiché quest’ultima non si esercita su cariche in quiete) ed in definitiva tra i capi A e B del conduttore si genera una differenza di potenziale. Sempre facendo riferimento alle equazioni di Maxwell, nel secondo caso, poiché il magnete è fisso ed è il conduttore che si sposta, la variazione dell’induzione magnetica B si avrà solo nel filo e non nell’etere circostante il magnete (caso del flusso tagliato). Quindi nell’etere non c’è una variazione del flusso di B e conseguentemente (per la stessa equazione di Maxwell precedentemente citata) non si originerà un campo elettrico nell’etere che circonda il magnete. Anche in questo caso però ai capi AB del conduttore si originerà una differenza di potenziale, ma questa volta di origine magnetica (forza di Lorentz). Questa differenza di potenziale, a parità di altri fattori, ha esattamente lo stesso valore che nel primo caso. (839)
Dall’esame di questa situazione, risultano dei fatti che sono certamente previsti dalla teoria di Maxwell-Lorentz, ma che, altrettanto certamente, sono tali da creare, per Einstein, una inaccettabile asimmetria; anche se gli effetti sono gli stessi (si producono nei due casi differenze di potenziale uguali, a parità di altre condizioni) i fenomeni hanno una spiegazione fisica differente: in un caso la differenza di potenziale è dovuta ad una forza elettrica, nell’altro ad una forza magnetica.
Poiché ciò che stiamo discutendo rivestiva grande importanza nel pensiero di Einstein (840) è utile fare un’altra esemplificazione, del tutto simile a quella ora discussa ma più facilmente comprensibile.
Supponiamo di avere due cariche elettriche q uguali poste ad una distanza r l’una dall’altra (per semplicità supponiamo che una di esse sia vincolata in modo tale che non possa muoversi). Un osservatore T, immobile rispetto al sistema costituito dalle due cariche, calcolerà, secondo le usuali leggi dell’elettrostatica, una forza F che agirà sulla carica mobile e diretta come in figura 42a (cariche dello stesso segno si respingono). Supponiamo ora che l’osservatore

T si sposti, con velocità u, nella direzione mostrata in figura 42b. Secondo il principio galileiano di relatività, tutto va come se T fosse immobile e fossero invece le cariche che si muovono alla stessa velocità di T ma in verso opposto (figura 42c). In questo caso, quindi, T osserverà due correnti parallele (una carica in moto costituisce una corrente elementare). Ora, secondo la legge di Ampère sulle azioni elettrodinamiche tra correnti, alla forza repulsiva F, che si aveva nel caso di azione elettrostatica (figura 42a), si deve sottrarre una forza attrattiva f (dovuta al fatto che correnti concordi si attraggono). In definitiva, un osservatore in moto dovrebbe calcolare (e calcola) una forza repulsiva F – f, minore della forza repulsiva F che lo stesso osservatore calcolerebbe (e calcola) quando è in riposo. E ciò vuol dire che le leggi dell’elettrodinamica danno risultati diversi per osservatori in moto relativo a velocità costante. Questo fatto può essere detto anche così: le leggi dell’elettrodinamica non sono invarianti per una trasformazione di Galileo. (841)
Come rendere conto di tutto ciò ?
Oltre a questo tipo di asimmetrie Einstein fa anche un vago riferimento ad altri fenomeni che probabilmente sono: l’aberrazione stellare, l’esperienza di Fizeau relativa alla misura della velocità della luce in due colonne di acqua fluente in versi opposti, (842) l’esperienza di Michelson-Morley, quella di Trouton-Noble. Bice Einstein:
“Esempi analoghi, come pure i falliti tentativi di constatare un moto della Terra relativamente al mezzo luminoso, conducono alla presunzione che al concetto di quiete assoluta, non solo nella meccanica, ma anche nell’elettrodinamica, non corrisponda alcuna delle proprietà di ciò che si manifesta, ma che piuttosto, per tutti i sistemi di coordinate per i quali valgono le equazioni della meccanica, (843) debbano anche valere le stesse leggi elettrodinamiche ed ottiche, come appunto è stato dimostrato per le grandezze del primo ordine.”
Einstein inizia a costruire la sua fisica dei principi con l’affermazione che il concetto di riferimento assoluto non ha alcun significato né nella meccanica né nell’elettrodinamica né nell’ottica. Piuttosto bisogna ammettere che tutte le leggi fisiche abbiano la stessa forma in tutti i sistemi inerziali. Non vi è quindi nessun sistema privilegiato in cui le cose debbano andare in un dato modo; al contrario tutti i sistemi inerziali, tutti quelli in moto relativo uniforme gli uni rispetto agli altri, sono equivalenti; in essi tutte le leggi fisiche devono essere le stesse. A questo punto Einstein dice:
“noi vogliamo elevare questa presunzione … a presupposto fondamentale”
ed in questo modo introduce il primo dei due principi che sono il fondamento della relatività, quello che va sotto il nome di Principio della relatività di Einstein. (844) Come si vede, si tratta di una generalizzazione del Principio di relatività di Galileo a tutte le leggi della fisica.
Subito dopo, a questo principio, Einstein ne aggiunge un altro:
“[noi vogliamo] inoltre introdurre il presupposto, solo apparentemente inconciliabile con il precedente, che la luce nello spazio vuoto si propaghi sempre con una velocità determinata e indipendente dalla velocità del corpo emittente.” (845)
Si tratta del principio che va sotto il nome di Principio della costanza della velocità della luce, quello che più ha fatto discutere (si veda, ad esempio, quanto sostiene M. La Rosa – 1923 – in bibl. 186, pagg. 293-306).
Da dove tira fuori questo principio Einstein ?
Esso era comunemente accettato in tutte le teorie ondulatorie della luce (Fresnel, Stokes, Maxwell, Lorentz) ma, sempre, come principio applicabile ad un sistema che si trovasse in riposo rispetto all’etere. Probabilmente il fatto che un valore costante di c venisse fuori dalle più disparate misure fatte sulla Terra, non importa in quale direzione rispetto al presunto etere, unitamente al fatto che questo valore si ricavasse da elaborazioni teoriche sulle equazioni che regolano i campi elettromagnetici (si ricordi il lavoro di Weber e Kohlraush), convinsero Einstein ad assumere la costanza di c come principio generale. Inoltre, forse, influì su Einstein proprio la formulazione del primo dei due principi, quello di relatività; se, infatti, la Terra si considera come un sistema inerziale e su di essa le misure di c danno sempre lo stesso valore, e deve avere lo stesso valore per tutti gli altri sistemi inerziali (indipendentemente dallo stato di moto della sorgente per il fatto che anche dalle misure fatte sulla Terra risulta questa indipendenza, infatti c ha lo stesso valore sia quando è misurata da fenomeni astronomici, sia quando è misurata su sorgenti poste sulla Terra, e lo stato di moto di una sorgente sulla Terra è certamente differente dallo stato di moto, ad esempio, di un satellite di Giove). (846) Infine, e questo è il fatto più importante, Einstein, nei suoi tentativi di modificare le equazioni di Maxwell-Lorentz perché risultassero invarianti per sistemi di riferimento in moto traslatorio uniforme gli uni rispetto agli altri, deve essersi convinto che la condizione che si richiedeva era la costanza di c.
Certo che questo principio, così formulato, doveva suonare male e, con Straneo, “forse sarebbe stato meglio porre in rilievo che la teoria dei gruppi imponeva l’adozione di una costante fondamentale e che questa per ragioni fisiche non poteva che essere la velocità della luce.” (847)
Comunque stiano le cose, Einstein dice che questo secondo Principio appare inconciliabile con il primo. Perché ?
Perché, ammesso il Principio di relatività, sembrerebbe che debbano valere le trasformazioni di Galileo e, in particolare, la composizione delle velocità. Supponiamo allora ai accettare contemporaneamente il Principio dell”indipendenza di c dal moto della sorgente e la composizione classica delle velocità: se una sorgente si muove verso un osservatore con velocità v, il tutto equivale a sorgente immobile ed osservatore che si sposta verso di essa con velocità – v; l’osservatore misurerebbe allora una, velocità u = c + v e dalla conoscenza di c egli sarebbe in grado di ricavare v e cioè una velocità assoluta; questo fatto entrerebbe in contraddizione con il supposto Principio di relatività. E l’apparente inconciliabilità sta proprio qui: il Principio di relatività di Einstein non prevede le trasformazioni di Galileo e quindi non prevede quella composizione delle velocità. Assumendo nuove trasformazioni l’inconciliabilità sparisce e la c, oltre ad assumere un valore costante in tutti i sistemi inerziali, diventa una velocità limite, una velocità che non può essere superata in alcun modo. (848) Ciò che si vuol dire è che l’apparente inconciliabilità nasce dalle ordinarie definizioni di spazio e di tempo. Ammessi i due Principi di Einstein, occorre cambiare queste definizioni e conseguentemente le loro equazioni di trasformazione (quelle di Galileo) nel passaggio da un sistema inerziale ad un altro.
Riassumendo, i due principi che Einstein pone a fondamento della sua elettrodinamica sono:
1) Principio di Relatività: Le leggi della fisica sono le stesse in tutti i sistemi inerziali animati di un moto rettilineo uniforme gli uni rispetto agli altri. Nessuno di questi sistemi inerziali è privilegiato.
2) Principio di costanza della velocità della luce: La velocità della luce nel vuoto ha sempre lo stesso valore c in tutti i sistemi inerziali. Essa è indipendente dalla velocità della sorgente o dell’osservatore.
Egli dice?
“Questi due presupposti bastano per giungere ad una elettrodinamica dei corpi in movimento semplice e libera da contraddizioni …”
E dell’etere, cosa ne è di questa misteriosa sostanza ?
“L’introduzione di un etere luminoso si manifesterà superflua …”
Così, con un solo colpo di penna, Einstein si sbarazza di ciò che da più parti veniva indicato come il tormento della fisica. L’etere se ne va, sparisce il riferimento assoluto e lo spazio assoluto (cosa che d’altra parte era implicita nel primo principio assunto da Einstein).
A questo punto sono dati i principi generali. Come intende proseguire Einstein ?
Proprio come indicavamo qualche riga più su a proposito dell’inconciliabilità: a partire da una revisione dei concetti fondamentali della meccanica e, in particolare, della cinematica (si noti: revisione della meccanica e non dell’elettrodinamica). Egli dice:
“La teoria da sviluppare si appoggia – come ogni altra elettrodinamica – sulla cinematica del corpo rigido, poiché le affermazioni di ogni teoria del genere riguardano rapporti tra corpi rigidi (sistemi di coordinate), orologi e processi elettromagnetici. Le non sufficienti considerazioni di questa circostanza sono la radice delle difficoltà con le quali l’elettrodinamica dei corpi in moto ha presentemente da lottare.”
Per costruire una elettrodinamica consistente con i suoi due principi, Einstein parte quindi da una ridefinizione di lunghezze e tempi che sono alla base di qualunque processo di misura, anche di fenomeni elettromagnetici, e che nel passato sono stati dati troppo facilmente per scontati.
Con ciò termina l’introduzione al suo articolo e passa a discutere, appunto, questioni di cinematica.

CINEMATICA

La prima, questione che viene affrontata è la definizione di contemporaneità o simultaneità.
Cosa si deve intendere per eventi simultanei ? Sembrerebbe di poter rispondere: eventi che avvengono nello stesso istante. Si, ma che significa nello stesso istante ?
Per rispondere a questa domanda Einstein si costruisce una serie di strumenti concettuali tali che gli permettano di arrivare ad una definizione operativa delle grandezze fisiche tempo (mediante orologi) e lunghezza (mediante regoli rigidi). (849) Seguiamo il suo ragionamento.
Egli inizia con l’introdurre un sistema inerziale che, per semplicità discorsiva, considera in quiete. Se si vuole definire la posizione di un punto materiale in questo sistema, lo si può fare misurando, con dei regoli rigidi, le distanze di questo punto dai tre assi cartesiani coordinati. Se si vuole definire il moto di questo punto materiale si possono dare le coordinate del punto in funzione del tempo. Ora, quando si parla di tempo, occorre fare attenzione. Infatti, parlare di tempo è come parlare di avvenimenti simultanei e questo perché se, ad esempio, noi diciamo che il treno arriva alle 7, intendiamo dire che il treno arriva simultaneamente a quando le lancette del nostro orologio segnano le 7. Si può allora sostituire la definizione di tempo con le posizioni delle lancette dell’orologio ? Questo va bene solo nel caso in cui si debba definire il tempo per il luogo dove si trova l’orologio; ma se si vogliono dare i tempi per “avvenimenti che si svolgono in luoghi differenti”, allora sorge la necessità di sapere cosa diventa quella simultaneità cui ci riferivamo prima. Noi potremmo certamente valutare il tempo in cui si produce un determinato fenomeno nello spazio a partire da un unico osservatore, munito di orologio, che si trovi nell’origine delle coordinate del nostro sistema inerziale: si produce l’avvenimento; esso viene segnalato all’origine delle coordinate con un segnale luminoso; quando il segnale luminoso arriva, l’osservatore va a vedere che tempo segna il suo orologio. Questo metodo però, osserva Einstein, “ha l’inconveniente di non essere indipendente dalla posizione dell’osservatore munito di orologio”; infatti, a posizioni diverse dell’osservatore, data la costanza di c (e qui non serve assumere la costanza di c per tutti i sistemi inerziali ma solo quella per un sistema in quiete), corrispondono tempi diversi per uno stesso fenomeno che avviene in un punto fissato dello spazio. (850) Einstein suggerisce quindi “una più pratica determinazione [per] avvenimenti che si svolgono in luoghi differenti” .
Supponiamo di prendere in considerazione due punti A e B dello spazio, nei quali si trovino due osservatori muniti di due orologi identici. L’osservatore A potrà dare i tempi di A e delle immediate vicinanze; l’osservatore B potrà dare i tempi di B e delle immediate vicinanze. Se però non si fa qualche altra convenzione
“non è possibile … paragonare temporalmente un avvenimento in A con un avvenimento in B; noi [infatti] abbiamo finora definito un tempo A e un tempo B, ma nessun tempo comune ad A e B.”
L’ulteriore convenzione che manca per definire quest’ultimo tempo è
“che il tempo che la luce impiega per giungere da A a B è uguale al tempo che essa impiega per giungere da B ad A.”
Data questa definizione è allora possibile sincronizzare due orologi distanti mediante un segnale luminoso che, partito da A, dopo la riflessione su B, riporti ad A l’informazione sul tempo di B. Chiamiamo con tA l’istante (il tempo) in cui un raggio di luce parte da A, con tB l’istante in cui questo raggio viene riflesso da B per tornare verso A e con t’A l’istante in cui il raggio arriva di nuovo in A. La definizione data ci permette di dire che i due orologi funzionano in modo sincrono quando:

t_B – t_A = t’_A – t_B . (851)

Con questa definizione non vi è luogo a contraddizioni e non solo per i punti A e B, ma per qualsiasi altro punto dello spazio, di modo che valgono le seguenti condizioni:
“1.Quando l’orologio in B cammina sincrono con l’orologio in A, l’orologio in A cammina sincrono con l’orologio in B.
2.Quando l’orologio in A cammina sincrono con l’orologio in B quanto anche con l’orologio in C, camminano pure sincroni gli orologi in B e in C relativamente l’uno all’altro.”
In questo modo, aiutandosi con esperienze mentali, Einstein fornisce una definizione di tempo e di simultaneità. In particolare, secondo Einstein,
“il tempo di un avvenimento è l’indicazione contemporanea all’avvenimento di un orologio in quiete, che si trova nel luogo dell’avvenimento, il quale procede sincrono con un determinato orologio in quiete, e precisamente per tutte le determinazioni di tempo, con lo stesso orologio.”
Come conseguenza di quanto detto ed in accordo con il Principio della costanza della velocità della luce, si ha:

(2 AB)/( t’_A – t_A ) = c

cioè: la velocità della luce, come costante universale, è data dal rapporto tra l’intero tragitto, andata e ritorno, tra A e B ed il tempo totale impiegato a percorrere questo tragitto. Come si ricorderà questi due punti, A e B, erano presi in un sistema in quiete, per cui
“il tempo ora definito, a cagione di questa appartenenza al sistema in quiete, lo diremo il tempo del sistema in quiete.” (852)
A questo punto si può cominciare a parlare di relatività di lunghezze e tempi introducendo nelle nostre discussioni e il Principio di relatività e quello della costanza della velocità della luce che vengono ora esplicitamente enunciati nel modo seguente:
“1) Le leggi secondo le quali si modificano gli stati dei sistemi fisici sono indipendenti dal fatto che questi e cambiamenti di stato vengano riferiti all’uno o all’altro di due sistemi di coordinate che si trovino in relativa reciproca traslazione uniforme.
2) Ogni raggio di luce si muove nel sistema di coordinate in quiete con la determinata velocità c, indipendente dal fatto che quel raggio di luce sia emesso da un corpo in quiete o da un corpo in movimento.”
Supponiamo di avere, nel definito sistema in quiete, un’asta rigida di lunghezza h (misurata nello stesso sistema in quiete con un regolo rigido). Quest’asta si trovi poggiata sull’asse delle x e, ad un dato istante, cominci a muoversi con velocità v nel verso delle x crescenti. Ci si chiede qual è la lunghezza di questa asta in due eventualità:
a) l’osservatore (853) è in moto con l’asta alla sua stessa velocità ed esegue la misura in questo sistema mediante un regolo rigido (il tutto va come se osservatore, asta da misurare, regolo di misura si trovassero in quiete);
b) l’osservatore è sul sistema in quiete; egli, mediante orologi (in quiete) sincronizzati con quelli (in moto) che si trovano sull’asta da misurare, “deduce … in quali punti del sistema in quiete si trovino il principio e la fine dell’asta da misurare, in un determinato tempo t”; a questo punto si passa a misurare la distanza di questi due punti, mediante un regolo rigido nel sistema in quiete. Anche questa dovrà essere considerata come lunghezza dell’asta.
Il principio di relatività ci dice subito che utilizzando il sistema di misura (a), “la lunghezza dell’asta in moto nel sistema in moto deve essere uguale alla lunghezza h dell’asta in quiete”; e ciò vuol dire che la misura che noi troviamo per l’asta è la stessa sia quando noi, stando in quiete, misuriamo l’asta in quiete nel sistema in quiete; sia quando noi, stando in moto, misuriamo l’asta in moto nel sistema in moto. (854)
Vediamo ora di calcolarci mediante (b) “la lunghezza dell’asta in moto nel sistema in quiete” e, come Einstein anticipa, troveremo che essa è differente dalla precedente lunghezza h, e ciò in contrasto con quanto la cinematica ordinaria generalmente ammette. Supponiamo di avere alle estremità A e B dell’asta due orologi sincronizzati con gli orologi del sistema in quiete; e ciò vuol dire che i tempi indicati dagli orologi che si trovano in A e B corrispondono, istante per istante, al “tempo del sistema in quiete”; e ciò vuol dire ancora che gli orologi che si trovano in A e B sono “sincronizzati nel sistema in quiete”. (855) Vi sia poi un osservatore vicino all’orologio A ed un osservatore vicino all’orologio B, di modo che i due osservatori si muovano con gli orologi. Questi osservatori dovranno sincronizzare gli orologi mediante il sistema di sincronizzazione dato precedentemente e cioè mediante un segnale luminoso. Allora, “al tempo t_A del sistema in quiete parta [da A] un raggio luminoso, venga riflesso al tempo t_B in B e ritorni al tempo t’_A in A”. Questo segnale impiegherà un tempo t_B – t_A per percorrere la distanza AB ed un tempo t’_A – t_B per percorrere la distanza BA. Ora, a seguito del principio della costanza della velocità della luce, il segnale luminoso che viaggia con velocità c: quando da A va verso B, dovrà rincorrere l’estremo B che gli si allontana con velocità v; quando da B torna verso l’estremo A, si troverà quest’ultimo che gli va incontro con velocità v. In definitiva, se con rAB denotiamo la lunghezza dell’asta misurata nel sistema in quiete, si ha: (857)

t_B – t_A = r_AB /(c – v) e t’_A – t_B = r_AB /(c + v)

Quanto ricavato vuol dire che “osservatori in moto con l’asta in moto troverebbero i due orologi non procedenti sincronicamente, mentre osservatori nel sistema in quiete dichiarerebbero, sincroni quegli orologi”. (858) E questo perché, mentre avevamo visto che per il sistema in quiete i due orologi situati in A e B erano sincroni con la conseguenza che per il sistema in quiete doveva risultare:

t_B – t_A = t’_A – t_B

ora, per il sistema in moto, risulta:

t_B – t_A ≠ t’_A – t_B.

Einstein può allora concludere:
” Vediamo dunque che al concetto di simultaneità non possiamo attribuire alcun significato assoluto, ma che invece due avvenimenti che, considerati da un sistema di coordinate, sono simultanei, considerati da un sistema mosso relativamente ad esso, non sono più da considerare come avvenimenti simultanei.”
In definitiva, il concetto di simultaneità, dato per evidente nella cinematica classica, viene a perdere il suo valore assoluto, diventando relativo. Inoltre si scambiano i ruoli preesistenti: mentre prima la definizione di tempo ci permetteva di parlare di eventi simultanei, ora la definizione di eventi simultanei ci permette una misura del tempo.
Abbiamo ora in mano tutte le premesse necessarie per costruirci le equazioni di trasformazione, quelle cioè che ci permettono di passare da un sistema supposto in quiete ad un altro in moto traslatorio uniforme rispetto al primo (e viceversa). Questa parte viene trattata da Einstein nel paragrafo 3 della sua memoria. Io, per ragioni di semplicità concettuale ed espositiva, (859) preferisco seguire un modo diverso per ricavare le stesse equazioni di trasformazione. Questa trattazione è stata elaborata dallo stesso Einstein in un’epoca successiva (1916). (860)

Questa seconda parte inizia con la trascrizione delle equazioni di Maxwell nella forma di Hertz per lo spazio vuoto. (872) Einstein quindi suppone che queste equazioni così scritte siano valide per il sistema di riferimento S (supposto in quiete). Osservando ora da S un fenomeno elettromagnetico che si svolge su S’ (supposto in moto uniforme con velocità v rispetto ad S), le equazioni che lo descrivono si dovranno ottenere applicando a quelle date su S le equazioni di trasformazione (8) da lui precedentemente trovate. La forma che egli trova per le equazioni di Maxwell-Hertz, scritte per il sistema S’ osservato da S, è differente dalla forma che esse avevano nel sistema S.
A questo punto interviene però il principio di relatività: le equazioni di Maxwell-Hertz per lo spazio vuoto debbono valere anche in S’, se valgono in S; e ciò vuol dire che queste equazioni debbono avere la stessa forma di quelle originariamente scritte per S, quando le scriviamo per il sistema S’ osservato dallo stesso S’.
Scritte quindi le equazioni di Maxwell-Hertz per il sistema di riferimento S’ (esse sono uguali a quelle scritte per S solo che ora le grandezze che vi compaiono sono grandezze di S’ e quindi hanno l’apice), Einstein osserva, che i due sistemi di equazioni ottenuti per il riferimento S’ (quello originato dalle equazioni di Maxwell-Hertz scritte per S e trasformate per S’ e quello scritto direttamente per S’) debbono esprimere la stessa cosa. (873) Affinché ciò accada , confrontando i due sistemi di equazioni con considerazioni di simmetria, si devono avere le seguenti equazioni di trasformazione per i campi elettrici E e magnetici H:

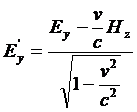
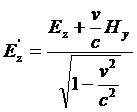
                                                                                                                     (14)

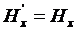
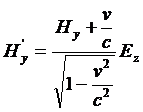
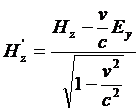
Con queste equazioni Einstein è in grado di dimostrare che tutte le asimmetrie alle quali aveva, accennato nell’introduzione del suo articolo, scompaiono e ciò senza alcun cambiamento di fondo nell’elettrodinamica, ma anzi fornendo una più profonda comprensione di essa.

        Per interpretare le (14) egli inizia con il considerare una carica elettrica puntiforme la quale, nel sistema in quiete S, sia unitaria (e ciò vuol dire che quando questa, carica è in quiete nel sistema S, esercita su un’altra carica unitaria alla distanza di 1 cm la forza di 1 dine). Secondo il principio di relatività questa carica sarà  unitaria anche se misurata nel sistema S’ in moto relativo con velocità v. Ora, se questa carica è in quiete relativamente ad S allora il vettore campo elettrico E, di componenti E_x,  E_y , E_z,  è uguale per definizione alla forza che agisce su di essa (indicando con q la carica unitaria si ha E = F/q) ; se invece questa carica è in quiete relativamente ad S’ (almeno nell’istante corrispondente) allora la forza che agisce su di essa, misurata in S’, è uguale al vettore E’, di componenti E’_x, E’_y., E’_z (anche qui, indicando con q’ la carica unitaria, si ha E’ = F’/q’).   (874)  Con quanto detto Einstein passa a confrontare la prima terna delle equazioni (14), quella relativa al campo E, con la vecchia formulazione e la nuova da lui proposta.

        Secondo la vecchia formulazione le (14), relative al campo E, si possono esprimere a parole nel modo seguente:

Se una carica elettrica puntiforme ed unitaria si muove in un campo elettromagnetico, la forza che agisce su di essa è uguale alla forza elettrica E esistente nel luogo dove si trova la carica; questa forza si ottiene per trasformazione del campo elettromagnetico in un sistema di coordinate che si trovi in quiete relativamente alla carica.

(Ed analoghe considerazioni possono essere sviluppate per le forze magnetomotrici).
Qual è allora la grande novità della nuova formulazione rispetto alla vecchia ? (876)
Nell’elaborazione della teoria di Lorentz, i moti relativi di una carica elettrica e di un campo magnetico erano sempre riferiti ad un etere immobile e quindi si poteva parlare di moto assoluto della carica elettrica o del campo magnetico rispetto all’etere. L’esistenza di questo moto assoluto, una volta del campo magnetico rispetto alla carica immobile relativamente all’etere ed una volta della carica rispetto al campo magnetico immobile relativamente all’etere (figura 41), fa nascere, rispettivamente, una volta una forza elettrica ed una volta una forza magnetica.
Nella teoria che ora propone Einstein non vi sono più moti assoluti rispetto all’etere. Anzi non vi è più nemmeno l’etere. Ora il crearsi di una forza elettrica o magnetica dipende solo dal moto relativo di carica elettrica e campo magnetico ed, in definitiva, dal solo moto dell’osservatore (a seconda che l’osservatore sia solidale con la carica elettrica o con il campo magnetico).
Ma è allora possibile che un dato campo sia una cosa o un’altra, a seconda del moto dell’osservatore ?
Il problema è risolto dalle equazioni di trasformazione (14): il campo elettrico ed il campo magnetico non hanno alcuna realtà indipendente, non esistono cioè fenomeni elettrici e magnetici gli uni distinti dagli altri; un campo che sia elettrico o magnetico in un dato riferimento ha sia componenti elettriche che magnetiche in un altro riferimento; il campo elettrico ed il campo magnetico non sono altro che casi particolari del più generale e dell’effettivo campo, quello elettromagnetico. (877) E’ il campo elettromagnetico che risulta indipendente dal moto dell’osservatore. Più in particolare, nell’esempio del moto relativo tra conduttore e magnete (si veda la figura 41), ma senza considerare l’etere): nel caso in cui l’osservatore e’ solidale con il conduttore (figura 41a) si osserva il sorgere di un campo elettrico e quindi di una forza elettromotrice nel caso in cui l’osservatore è solidale con il magnete (figura 41b) si osserva il sorgere di una stessa forza elettromotrice, originata dalla vecchia concezione della forza (magnetica) di Lorentz. Ora, con le equazioni (14) questa forza di Lorentz, nel passaggio da un sistema ad un altro (dal sistema in cui l’osservatore è solidale con il magnete a quello in cui è solidale con il conduttore), non rappresenta altro che un campo elettrico. (878)
Lo stessa Einstein così conclude questa parte del suo articolo:
“Si vede che nella teoria sviluppata la forza elettromotrice ha solo il ruolo di un concetto ausiliario, il quale deve la sua introduzione alla circostanza che le forze elettriche e magnetiche non hanno alcuna esistenza indipendente dallo stato di moto del sistema delle coordinate.
E’ inoltre chiaro che le asimmetrie citate nell’introduzione riguardanti le correnti prodotte per mezzo di moti relativi di un magnete e di un conduttore spariscono. Anche le questioni relative alla ‘sede’ delle forze elettromotrici elettrodinamiche (macchine unipolari) divengono prive di significato.” (879)
Con la revisione del concetto di tempo, a partire da una ridefinizione di simultaneità, Einstein è riuscito a mettere a posto le asimmetrie nei fenomeni elettromagnetici delle quali ha parlato nell’introduzione. Nel far questo si è sbarazzato del concetto di etere ed ha costruito le basi per una ridefinizione unitaria dei concetti meccanici ed elettrodinamici.
Le prime applicazioni di quanto fin qui trovato vengono subito dopo, nel seguito dell’articolo.
Il paragrafo 7 si occupa della Teoria del principio di Doppler e della aberrazione, mentre il paragrafo 8, Trasformazione dell’energia dei raggi luminosi, tratta del problema della pressione di radiazione. Non tratterò qui di queste applicazioni della relatività ma mi riservo di farlo per alcuni di questi fenomeni e per altri nel prossimo paragrafo, dove tratterò in modo più semplificato ed intuitivo quanto fino ad ora visto a proposito di relatività. Per ora basti osservare che i paragrafi 7 ed 8 sono un ulteriore esempio del metodo einsteniano: prima sono stati formulati i due principi alla base della relatività, sui quali è stata appunto costruita una teoria fisica basata su poche, semplici ed essenziali, ipotesi quindi si va ad applicare questa fisica a fenomeni particolari.
Nell’economia del nostro lavoro solo due parole possiamo dedicare al paragrafo 9 dell’articolo. Trasformazione delle equazioni di Maxwell-Hertz con considerazione delle correnti di convezione, nel quale si affronta il problema della conservazione della carica nel passaggio da un riferimento ad un altro in moto traslatorio uniforme rispetto al primo.
Einstein si riscrive ora le equazioni di Maxwell-Hertz introducendo in esse le ‘correnti di convezione’ e cioè esprimendo le componenti (Ex, Ey, Ez ) del vettore campo elettrico E in funzione della densità di corrente e della velocità con cui si sposta l’elettricità. Egli osserva quindi che
“se si pensano le masse elettriche invariabilmente legate a piccoli corpi rigidi (ioni, elettroni) queste equazioni sono le basi elettromagnetiche dell’elettrodinamica ed ottica dei corpi in movimento di Lorentz.”
Supposte allora valide queste equazioni per il riferimento S considerato in quiete, le possiamo trasformare mediante le (8) e le (14) in modo che esse ci descrivano gli stessi fenomeni per un riferimento S’, considerato in moto con velocità v rispetto ad S. Da questa trasformazione Einstein ricava, con lo stesso metodo ‘di confronto’ utilizzato per ricavare le (14) e come conseguenza del teorema di composizione delle velocità, un vettore che rappresenta la velocità di quelle masse elettriche misurata nel sistema S’. Einstein può così affermare che
“è dimostrato che la base elettrodinamica della teoria elettrodinamica dei corpi in movimento di Lorentz, secondo i nostri principi cinematici, corrisponde al principio della relatività.”
Infine egli ricava
“il seguente importante teorema: se un corpo elettricamente carico si muove ad arbitrio nello spazio e con ciò non cambia la sua carica, considerata da un sistema di coordinate che si muova col corpo, la sua carica rimane anche costante, considerata dal sistema in quiete S.”
E quest’ultimo teorema non esprime altro che l’invarianza della carica elettrica nel passaggio da un riferimento ad un altro e cioè che la carica elettrica non dipende dal suo moto.
Il paragrafo 10, ultimo dell’articolo, merita invece una, certa attenzione. In esso Einstein, partito dalla cinematica, inizia, l’elaborazione di una dinamica. Il titolo del paragrafo è: Dinamica dell’elettrone (lentamente accelerato); vediamone il contenuto. (880)
Supponiamo di avere un elettrone di carica e che si muova all’interno di un campo elettromagnetico sotto le seguenti ipotesi; esso è stato appena messo in moto, con piccola accelerazione; la forza elettrica f = eE che agisce su di esso produce l’accelerazione a della sua massa mo, di modo che risulta f = mo a ed in definitiva si ha mo a = eE , oppure, esprimendo questo ultimo risultato secondo le componenti ax, ay , az del vettore accelerazione e le componenti Ex , Ey , Ez del vettore campo elettrico,

m_oa_x = eE_x

m_oa_y = eE_y

m_oa_z = eE_z

dove m_o e’ la massa dell’elettrone fintantoché la sua velocità è molto piccola rispetto alla velocità della luce. (881)
Supponendo che, ad un dato istante, l’elettrone sia. dotato di una velocità v, vogliamo calcolarci la legge del moto per l’elettrone nell’istante successivo. Per semplicità, supponiamo ancora che all’istante t = 0, istante in cui cominciamo a considerare il fenomeno, l’elettrone si trovi nell’origine delle coordinate e inizi a muoversi con velocità v lungo l’asse delle x (nel verso delle x crescenti). Le cose vanno allora come se l’elettrone si trovasse in quiete in un sistema di riferimento S’ in moto con velocità v, (882) lungo il verso delle x crescenti, rispetto ad un riferimento S considerato in quiete. Quali sono allora le leggi che regolano il moto dell’elettrone, osservato da S’, nell’istante immediatamente successivo all’inizio del moto ? Il principio di relatività ci dice che i fenomeni si debbono svolgere allo stesso modo nei due riferimenti e che si deve perciò avere

m_oa’_x = eE’_x

m_oa’_y = eE’_y

m_oa’_z = eE’_z

    moax = eβ-3Ex

    moay = eβ-1Ey                                          (15 bis)

    moaz = eβ-1Ez

dove i simboli a’_x, a’_y, a’_z, ed E’_x, E’_y, E’_z, sono riferiti al sistema S’. Imponiamo inoltre che per t = x = y = z = 0 debba risultare t’ = x’ = y’ = z’ = 0; valgono allora le equazioni di trasformazione (8), per il tempo e le coordinate, e (14), per il campo elettrico. “Con l’aiuto di queste equazioni trasformiamo le equazioni del moto ottenute sopra, dal sistema S’ al sistema S ’’, ed avremo, avendo indicato con β la quantità
β = (1 – v2/c2)- 1/2 : (883)

m_oa_x = eβ^-3E_x

   m_oa_y = eβ^-1E_y                                          (15 bis)

            m_oa_z = eβ^-1E_z

le quali si possono anche scrivere:

        m_oβ³a_x = eE_x

         m_oβ a_y = e [E_y – (v/c) H_z]                                                     (15)

               m_oβ a_z = e [E_z + (v/c) H_y]

E fin qui nulla da dire. A questo punto però Einstein “commise la svista di applicare ancora la meccanica newtoniana al moto dell’elettrone.” (884) Seguiamo i suoi successivi passaggi. Egli si rende conto di avere al primo membro delle (15) delle forze. Al secondo membro, invece, almeno così sembra, che pensasse Einstein nel 1905, non ha delle forze (a parte la prima delle 15). Basta però moltiplicare per β ambedue i membri delle ultime due relazioni (15) per ottenere :

            m_oβ³a_x = eE_x

            m_oβ²a_y = eβ [E_y – (v/c) H_z]                                                    

                  m_oβ²a_z = eβ [E_z + (v/c) H_y]

e, ricordando le (14), si ha subito:

                          m_oβ³a_x = eE’_x

                            m_oβ²a_y = eE’_y                            (16)

                                   m_oβ²a_z = eE’_z

A questo punto, al secondo membro delle (l6), Einstein ha le componenti eE_x, eE_y, eE_z della forza elettromotrice che agisce sull’elettrone, considerate nel sistema di riferimento che si muove con l’elettrone, con la sua stessa velocità (in quel momento).  (885)   Egli chiama questa forza,  “la forza agente sull’elettrone” ed utilizza la legge newtoniana che fornisce la forza:

grandezza della massa moltiplicata per grandezza dell’accelerazione = grandezza della forza

Si deve subito osservare che non è più possibile utilizzare questa relazione (almeno all’interno della meccanica relativistica.) .Essa si fonda infatti sul concetto classico di quantità di moto (mv) e di sua variazione nell’unità di tempo Δ(mv)/Δt. Ora, supponendo di non sapere ancora che la massa m non è più costante, la relazione che ci dà la variazione della quantità di moto nell’unità di tempo diventa:

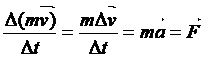
Ebbene, dato che conosciamo già la composizione relativistica delle velocità, non è più possibile fare i passaggi che abbiamo fatto, infatti quel Δv che compare nel primo passaggio dovrà essere modificato secondo la composizione relativistica, delle velocità. Inoltre, supponendo di sapere già che la massa
non è più costante, nessuno ci autorizza più a fare il primo passaggio; non è cioè possibile tirar fuori da un simbolo di variazione (Δ) una quantità variabile (m). In ultima analisi si può soltanto accettare la prima relazione uguagliata con l’ultima, e cioè:

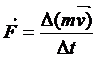
o meglio     

il che vuol dire che come definizione di forza dobbiamo assumere:

grandezza della forza = variazione della quantità di moto nell’unità di tempo

[o meglio: grandezza della forza = derivata rispetto al tempo della quantità di motoJ.
E questo per ciò che riguarda la definizione della forza data da Einstein. C’è poi un altro aspetto del problema. Einstein, come abbiamo visto, credette di poter indicare la forza elettromotrice che agisce sull’elettrone con le sue componenti eEx, eEy , eEz, anche nel sistema S. Tuttavia, come dice Pauli, (886) in meccanica relativistica si mostra che la definizione di forza elettromotrice, più opportuna e più naturale, per una carica che si muova in un campo elettromagnetico, di moto qualsiasi, è la forza, di Lorentz. “Si mostra cioè che solo con questa definizione è possibile esprimere la forza come derivata temporale di una quantità di moto, che nei sistemi isolati si conserva.” (886)
Queste difficoltà, presenti nella prima formulazione di Einstein della relatività, furono messe in evidenza ed in gran parte risolte da Plance (887) in una sua memoria del 1906. (888) Lo stesso Einstein le riconobbe subito fondate, tant’è vero che nelle ristampe successive del suo articolo del 1905 aggiunse delle note in questo senso. Una di queste dice:
“La definizione della forza qui data non è vantaggiosa, come per primo fu dimostrato da M. Planck. E’ assai più utile definire la forza in modo che il teorema dell’impulso e il teorema dell’energia assumano la forma, più semplice.” (889)
Ritornando alle (l6), vediamo come prosegue Einstein.
Egli, data la sua definizione di forza ‘meccanica’ e di forza elettromotrice, poiché ha forze ai primi ed ai secondi membri, può riconoscere in m_oβ³, m_oβ², m_oβ² delle masse ed in particolare le masse longitudinale e trasversale:

massa longitudinale = m_oβ³ = 

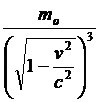
massa trasversale     = m_oβ² =

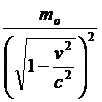
e questo nelle ipotesi che l’accelerazione che compare nelle (16) sia misurata nel sistema S supposto in quiete. Come si può subito vedere le relazioni trovate da Einstein per le masse longitudinale e trasversale non sono in accordo con quelle trovate da Lorentz [si vedano le (8) ed (8 bis) del paragrafo 5 del capitolo 4]. In particolare per la massa trasversale Lorentz aveva trovato un valore m_oβ . Ma, assumendo le correzioni di Planck, partendo cioè dalle (15) e non dalle (16) si arriva ad un completo accordo (si veda allo scopo lo scritto di Planck citato in nota 668). In definitiva:

(17)

massa longitudinale =

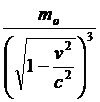
massa trasversale     =

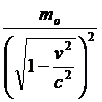
Lo stesso Einstein, in un’altra nota successiva al suo articolo, si rende conto dell’arbitrarietà della definizione della forza che, a priori, dipende dalle (15). Egli aggiunse infatti queste parole:

“Naturalmente per altre definizioni della forza e dell’accelerazione si otterrebbero altri valori per le masse; si vede da ciò che, nel comparare diverse teorie del moto dell’elettrone, si debba procedere con prudenza.”  (890)

        A questo punto del suo articolo Einstein, dopo aver osservato che questi ultimi risultati valgono anche per punti materiali ponderabili che diventano elettroni quando a loro si aggiunga una carica elettrica,  (890 bis) passa a. discutere dell’energia che compete all’elettrone che si muove, secondo le modalità viste prima, in un campo elettromagnetico.

        Supponiamo che un elettrone si muova lungo l’asse x del sistema S (supposto in quiete) sotto l’azione del campo elettrico E e quindi della forza eE_x. L’energia necessaria a che il moto dell’elettrone si realizzi è evidentemente fornita dal campo. Poiché l’energia che richiede l’elettrone per spostarsi è data dalla forza cui è soggetto moltiplicata per lo spostamento, per un dato spostamento Δx l’energia ΔW necessaria all’elettrone e’ data da:

ΔW = F. Δx

e cioè:

ΔW = eE_x Δx.                             (18)

Per uno spostamento complessivo composto da tanti piccoli spostamenti Δx, l’energia W necessaria sarà:

W = Σ eE_x Δx                           (19)

dove il simbolo Σ sta per somma e, cioè, l’energia totale sarà data dalla somma di tutte le energie necessarie per ogni spostamento Δx. Nel caso si abbia a che fare con spostamenti infinitesimi dx l’energia necessaria all’elettrone sarà anch’essa infinitesima e varrà dW, di modo che la (l8) assumerà la forma:

dW = eE_x dx

e, per uno spostamento composto da tanti spostamenti infinitesimi dx, l’energia totale W necessaria sarà, analogamente alla (l9), data da:

necessarie ad ogni spostamento infinitesimo dx. Ora, l’energia rappresentata dalla (20) è energia che il campo deve fornire all’elettrone, il quale, si ricordi, essendo lentamente accelerato, non può perdere energia sotto forma di radiazione elettromagnetica. Inoltre l’energia che il campo fornisce all’elettrone diventa energia cinetica dell’elettrone e quindi le due energie dovranno poter essere uguagliate

Anche l’energia cinetica sarà data dal prodotto della forza, (questa volta meccanica) cui è soggetto l’elettrone, moltiplicata per un dato spostamento Δx. Tenendo presente la prima delle (15) che per la forza meccanica dà il prodotto della massa longitudinale m_oβ³ , per l’accelerazione a_x, per l’energia cinetica ΔW che compete all’elettrone si avrà:

ΔW = m_oβ³. a_x Δx

Anche qui, per uno spostamento complessivo composto da tanti spostamenti Δx, si avrà:

W = Σ m_oβ³. a_x Δx

e, nel caso gli spostamenti siano infinitesimi (dx) si avrà:

ricordando che dx/dt = v è una velocità, tenendo conto che l’integrale deve essere esteso a tutti gli elementi m_oβ³v compresi dal momento in cui l’elettrone è fermo (v = 0) al momento in cui l’elettrone ha acquistato la velocità v, si ha:

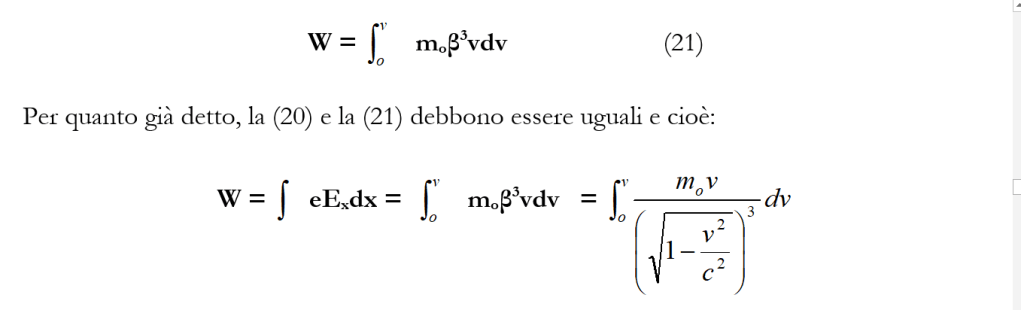
Calcolando l’integrale si trova:   (891)

cioè infinitamente grande e ciò vuol dire che per far marciare un elettrone alla velocità della luce occorre fornirgli una energia infinita. E naturalmente, anche qui come nei risultati precedenti, non ha senso pensare a velocità superiori a c. Inoltre, dice Einstein, la relazione (22) deve valere anche per masse ponderabili. E, dopo aver ricavato alcuni risultati “espressione delle leggi secondo le quali conformemente alla presente teoria deve muoversi l’elettrone”, Einstein conclude questo lavoro ringraziando il suo amico Michele Besso per il sostegno che gli fornì nell’elaborazione dell’articolo.

NOTE

(826) Annalen der Physik, 17; 1905; pagg. 891-921. Una traduzione in italiano di questo lavoro si trova in bibl.174, pagg.479-504. A questa mi riferirò.
(827) Annalen der Physik,18; 1905; pagg. 639-641. Una traduzione in italiano di questo lavoro si trova in bibl. l74 pagg. 505-50 7. A questa mi riferirò.
(828) La famosa relazione E = mc2 sarà ricavata da Einstein in un lavoro del 1907 pubblicato nel Jahrbuch der Radioaktivität.
(829) Una breve considerazione la merita questo aggettivo. Einste in era quel che si dice un. outsider. Egli correva al di fuori degli ippodromi universitari e non doveva rendere conto al suo cattedratico. La parte predominante della sua formazione si era costruita al di fuori dell’Università. Era un autodidatta. Spesso non andava a lezione e si presentava a far esami con i preziosi appunti che gli passava il suo amico Grossmann. Il suo professore H. Weber una volta ebbe a dirgli “Lei è un giovane intelligente, ma ha un difetto. Non consente a nessuno di insegnarle qualcosa”.
Per altri versi lo stesso Einstein riconobbe l’importanza di non stare dentro l’ambiente accademico; più volte egli sosterrà che la fisica, teorica la può far meglio un fontaniere o un ciabattino che possono dedicarsi a pensare ai problemi importanti senza l’ossessione di dover rendere conto della propria vita attraverso il susseguirsi di tante inutili pubblicazioni (e l’impiego all’Ufficio Brevetti era considerato da Einstein il suo essere ciabattino).
Allo stesso modo dell’altro outsider, Faraday, Einstein può permettersi di rimettere in discussione i concetti più consolidati nel campo della fisica, e soprattutto gli stessi metodi che presiedono la ricerca. Così come sui quanti di luce, Planck non aveva avuto il coraggio di fare il passo decisivo, allo stesso modo né Lorentz né soprattutto Poincaré l’avevano fatto sul problema relatività. Questi due passi li fece Einstein.
Si noti a parte che Planck per molto tempo avverserà la soluzione dei quanti di luce di Einstein. Al contrario Planck fu il primo fisico di fama che accettò e lavorò sulla relatività con importanti contributi (già nel 1906 e 1907 usciranno suoi articoli in proposito); tra l’altro, molto probabilmente, si deve a Planck, che stava nella redazione degli Annalen, se il lavoro di Einstein sulla relatività fu pubblicato.
(830) Dice Einstein nelle Note autobiografiche (bibl. l68, pag. 33): ” La teoria della relatività particolare deve la sua origine alle equazioni di Maxwell del campo elettromagnetico.” Ricordiamo che Einstein aveva trovato difettose le equazioni di Maxwell nella spiegazione del problema del corpo nero e dell’effetto fotoelettrico. Inoltre queste equazioni fornivano previsioni non corrette sulla pressione di radiazione.
(83l) Lo psicologo M. Wertheimer, amico di Einstein, scrive (citato da Hirosige; bibl. 124, pag.54): ” Se le equazioni di Maxwell sono valide rispetto ad un sistema, esse non sono valide in un altro. Esse dovrebbero essere cambiate … Per anni Einstein tentò di chiarire il problema studiando e cercando di modificare le equazioni di Maxwell. Non ebbe successo …”
(832) Bibl. 168, pag. 20.
(833) Dice Tarsitani (bibl. 170, pag.304) che la situazione nella quale si trovava ad operare Einstein era la seguente: “Elettrodinamica e termodinamica entrano in contraddizione quando si tratta di affrontare il problema della radiazione termica, meccanica e termodinamica, entrano in contraddizione nell’interpretazione statistica della seconda legge …, meccanica ed elettrodinamica si scontrano sul piano del principio di relatività e della dinamica dell’elettrone.”
(834) Bibl.168, pag. 28. Nella stessa pagina si trovano anche le citazioni precedenti senza indicazione bibliografica.
(835) Per due obiezioni a questo paradosso si veda bibl. 111, pag. 350 (nota 8) e bibl.128, pagg. 300-301. Questo paradosso, a ben guardarlo, è un gatto che si morde la coda poiché dà già per scontata una delle affermazioni fondamentali della relatività, la costanza della velocità della luce per tutti gli osservatori.
(836) Si tratta di un bel lavoro a fumetti. Bibl. 175, pag. 191.
(837) Bibl. 174, pag. 479. Tutte le citazioni che seguiranno senza riferimento bibliografico sono tratte, salvo avviso contrario, da questo testo di bibliografia, da pag. 479 a pag. 504.
(838) Una discussione dettagliata dei due casi d’induzione si può trovare su La Fisica di Berkeley (bibl. 176, Vol II, pagg. 265-280). Si noti però che questa trattazione dà già per scontata le non esistenza dell’etere.
(839) In questo caso la differenza di potenziale tra A e B nasce a seguito della forza di Lorentz (che abbiamo incontrato all’inizio del paragrafo 5 del capitolo 4). Si hanno infatti delle cariche (quelle che sono all’interno del conduttore) che si muovono all’interno di un campo magnetico. Queste cariche saranno soggette alla forza di Lorentz che risulta perpendicolare al piano formato dalla direziono del campo e da quella del suo spostamento. In particolare gli elettroni tenderanno ad accumularsi ad un estremo del circuito (finché non si raggiunga l’equilibrio con il campo elettrostatico che così si genera) dando così origine alla differenza di potenziale in oggetto.
(840) Sul fatto che l’asimmetria in oggetto rivestisse per lui grande importanza è dimostrato anche da uno scritto inedito di Einstein (datato circa 1919) nel quale, tra l’altro, egli afferma che un’asimmetria dello stesso genere lo condusse alla Relatività Generale. Allo scopo si può vedere G. Holton, The American Scholar, Vol. 41, inverno1971-1972, pagg. 95-100 (bibl. 127, pagg. 306-307) .
(841) Se si osserva che tutto ciò che ci circonda è costituito da particelle cariche ci si rende conto che è impossibile distinguere la dinamica, dall’elettrodinamica. Ed allora, o si mette a posto l’elettrodinaniica, o si rinuncia al principio classico di relatività, o si costruisce una nuova meccanica. La strada che seguirà Einstein sarà, come vedremo, l’ultima.
(842) Nell’intervista scritta di Shankland ad Einstein, già citata, Einstein, oltre all’esperienza di Michelson-Morley di cui aveva una conoscenza indiretta, fa riferimento proprio all’aberrazione ed all’esperienza di Fizeau (bibl.120, pag.35). Si noti che, nella stessa intervista, Einstein sostiene: “Ciò che mi ha condotto più o meno indirettamente alla teoria della relatività era la convinzione che la forza elettromotrice che agisce su un corpo in moto in un campo magnetico non è altro che un campo elettrico.” In questo modo, l’asimmetria, di cui abbiamo parlato prima, sparisce. Ma per ottenere questo occorreva, appunto, la teoria della relatività.
(843) Si sta parlando di sistema inerziali. E’ interessante osservare che questo concetto, oggi così diffuso e quasi indispensabile, fu introdotto solo nel 1885 dal fisico tedesco L. Lange (l863- ? ) nel suo lavoro Sulla formulazione scientifica della legge d’inerzia di Galileo. Egli propose di riferire la legge d’inerzia non più ad uno spirituale spazio assoluto ma, appunto, ad un sistema inerziale, ad un sistema di riferimento cioè rispetto al quale quella legge rimane valida (bibl .10, pag. 123).
(844) Si noti che il riferimento che Einstein fa (“… come è stato dimostrato per le grandezze del primo ordine”) mostra la sua conoscenza del lavoro di Lorentz del 1895 senza la parte – l’Appendice – in cui, con l’introduzione dell’ipotesi della contrazione, il fisico olandese mostrava di poter rendere conto dei fenomeni anche al secondo ordine. Si noti ancora che il cosmologo H. Bondi osserva: ” Sarebbe intollerabile che tutti i sistemi inerziali fossero equivalenti da un punto di vista dinamico, ma distinguibili mediante misure ottiche.” Si noti infine che un altro modo di enunciare il principio di relatività di Einstein è il seguente: ” Un osservatore che sia dotato di un moto traslatorio uniforme, non può decidere né con esperienze meccaniche, né con esperienze elettrodinamiche, né con esperienze ottiche, se egli si trovi in stato di quiete o di moto.
(855) Einstein, per la velocità della luce usa il simbolo V. Ho creduto opportuno sostituire questa notazione con quella, c, a noi più famigliare. Allo stesso modo ho operato per altre notazioni da noi oggi poco usate. In particolare, alla traduzione di Straneo di contemporaneità ho sostituito simultaneità. Si noti che, nelle ipotesi di Einstein, la velocità della luce deve essere indipendente sia dalla velocità del corpo emittente sia dalla velocità dell’osservatore, e ciò risulta chiaramente da un altro enunciato che Einstein fornisce per questo Principio nella stessa memoria (bibl 174, pag.482 ; è il punto 2 del secondo paragrafo della memoria in oggetto).
(846) Berkson fa rilevare che forse Einstein si costruì un’immagine dell’etere “come un lago e del sistema in moto come una barca a vela che si sposta in esso. Se ci sporgiamo e colpiamo l’acqua con un remo (sorgente luminosa), si emetteranno delle onde (luce) dal luogo dove abbiamo agitato l’acqua. La velocità delle onde cosi prodotte dipenderà dalla natura e dalla profondità dell’acqua (etere), ma non dalla velocità della barca attraverso l’acqua (velocità della sorgente).”
(847) Bibl. 174, pag.99. Su questo argomento torneremo più oltre, per ora si osservi che nel 1908 il fisico svizzero W. Ritz (1876-1909) elaborò una elettrodinamica fondata sul solo principio einsteniano di relatività, respingendo quindi la costanza di c in tutti i sistemi inerziali. Nella sua teoria (Annalen de Chimie et de Physique, 8; 1908) la luce era costituita da minuscole particelle (i quanti di luce introdotti da Einstein nel 1905) scagliate dalla sorgente in tutte le direzioni (l’analogo della teoria corpuscolare di Newton). Ebbene queste particelle hanno una velocità costante solo rispetto al corpo che emette la luce (e non, come in Einstein, in tutti i riferimenti inerziali). La teoria di Ritz, senza introdurre né tempo locale, né contrazioni, rendeva conto di tutti i fenomeni noti (compresa l’esperienza di Michelson). Solo nel 1939 fu scoperto da H.E. Ives, l’effetto relativistico Doppler trasversale che non si concilia con questa teoria mentre è in accordo con quella di Einstein. Ritz comunque non poté portare a termine il suo programma perché morì prematuramente nel 1909. Una discussione ad alto livello della teoria di Ritz è fatta da Pauli ( bibl, 179, pagg. 10-15 ).
(848) Avremo modo di soffermarci più oltre delle verifiche sperimentali della Relatività; per ora basti dire che la costanza di c e la sua indipendenza dalla velocità della sorgente o dell’osservatore, risulta con chiarezza da due fenomeni esemplari: la sua misura utilizzando come sorgente le stelle doppie e la sua misura dal decadimento della particella ° (pai zero).
(849) Colui che per primo formulò in modo esplicito l’operazionismo fu il fisico statunitense P.W. Bridgman (l862-1961) . Per eliminare dalla fisica e dalla scienza in genere molti concetti metafisici, Bridgman propose (1927) di definire i vari concetti che si utilizzano nella fisica in termini di operazioni o processi (di misura, di laboratorio, …). In un suo saggio, Le teorie di Einstein da un punto di vista operativo, inserito nel volume curato da Schlipp, Albert Einstein, scienziato e filosofo (bibl.168, pagg. 281-301), Bridgman afferma che colui che ha, nei fatti, inventato l’operazionismo è stato proprio Einstein con la sua Teoria della relatività ristretta. Dice Bridgman in apertura del saggio: ” Questa esposizione tenterà di dimostrare che Einstein non riportò nella sua relatività generale la profondità e gli insegnamenti che egli stesso ci aveva dato con la sua teoria particolare.” Einstein quindi, almeno con la sua relatività generale, abbandonò il punto di vista operativo nella definizione delle grandezze. Sul l’argomento si veda anche Bergia in bibl. 148, pagg. 37-38.
(850) Si noti che un’altra possibilità di dare i tempi per avvenimenti che si svolgono in luoghi differenti potrebbe essere quella di portare gli orologi nello stesso luogo, sincronizzarli e quindi riportarli nei luoghi d’origine. Einstein non prende in considerazione questa possibilità perché, probabilmente, aveva in mente due difficoltà: chi garantisce che il moto non alteri il funzionamento degli orologi ? e chi ci assicura che per due fenomeni differenti i tempi passino allo stesso modo ? Si ricordi che quella di Einstein è una definizione operativa.
(851) In definitiva, per sincronizzare un orologio che sta in A con uno che sta in B, si invia un segnale luminoso da A a B e si attende che ritorni in A. Alla fine dell’esperimento il tempo totale letto sa A, diviso per due, permette di sincronizzare i due orologi.
(852) Si noti che, in accordo con il Principio di relatività, tutti i sistemi inerziali sono equivalenti. Scelto un sistema inerziale a caso, nessuno ci vieta di considerarlo come se fosse in quiete (ed il fatto è in accordo anche con il principio classico di relatività). Occorre comunque ricordare che, dato un sistema inerziale, tutti quei sistemi che si muovono di moto rettilineo uniforme rispetto a quello, sono anch’essi inerziali.
(853) Taylor, in un modo divertente, fa rilevare: ” in queste spiegazioni intervengono sempre gli osservatori, i quali non possono neppure dormire perché, se lo facessero, potrebbero perdersi qualche avvenimento importante e mettere in crisi l’intera teoria” (bibl. 177, pag.86). Sulla abbondanza degli osservatori nella relatività basta tener sempre presente che l’osservatore non è né un fisico né un filosofo; non é uno che fa teorie ma, al contrario, è un esecutore materiale di misure, un operatore metrico.
(854) Se qualcuno, che ha già una qualche conoscenza di relatività, pensasse a per ora non meglio specificate contrazioni dell’asta, tenga conto che le contrazioni riguardano anche il regolo di misura. Ma su questo torneremo più oltre.
(855) Cioè: nel sistema in quiete risulterà, come abbiamo visto, tB – tA = t’A – tB . Il che vuol dire che: l’orologio che si trova in A indicherà il tempo di A nel luogo in cui si trova A; l’orologio che si trova in B indicherà il tempo di B nel luogo in cui si trova B; sia l’orologio di A che quello di B indicheranno il tempo del sistema in quiete; nel sistema in quiete i due orologi risulteranno sincroni.
(856) Come lo stesso Einstein ci fa osservare, questo tempo del sistema in quiete è anche la “posizione delle lancette dell’orologio del sistema in moto” che si trova nel luogo di cui si parla.
(857) Se si ricorda l’enunciato originale di Einstein del principio di costanza della velocità della luce (dato appena qualche riga più su), si riconoscerà che la velocità della luce, nel sistema in quiete, deve essere c. Ciò vuol dire che gli orologi del sistema in quiete misureranno un tempo maggiore per la luce che va da A a B rispetto a quello necessario alla luce per andare da B ad A. In un caso infatti bisognerà tener conto del fatto che la luce emessa da A deve raggiungere B che si allontana con velocità v; nell’altro caso, la luce riflessa da B dovrà raggiungere A che si avvicina con velocità v.
(858) Facendo seguito a quanto detto nella nota precedente, se gli orologi che si trovano in moto agli estremi dell’asta in movimento sono sincronizzati con il metodo di Einstein, rispetto al sistema in quiete daranno, tra loro e istante per istante, letture differenti. Ma poiché il principio della costanza di c è affermato per tutti i sistemi inerziali, noi dobbiamo ammettere che gli orologi nel sistema in moto, sincronizzati tra loro con il solito metodo, sono effettivamente sincroni tra loro.
(859) II modo con cui Einstein ricava le equazioni di trasformazione nella memoria del 1905 è, per noi, complesso per due motivi: 1) si introducono le equazioni alle derivate parziali che non conosciamo (non tutti almeno); 2) si svolgono dei ragionamenti un poco farragginosi (a posteriori!).
(860) In un lavoro divulgativo dal titolo Sulla relatività speciale e generale, bibl. 178. In particolare la trattazione che ci riguarda è in appendice, al paragrafo 11, pagg 68-70. Anche qui ho cambiato alcune notazioni di Einstein in modo da renderle conseguenti con altre notazioni da me usate in altra parte di questo lavoro.

(872) Si tratta di 6 equazioni differenziali che legano tra di loro le componenti vettoriali dell’intensità (forza) del campo elettrico (Ex , Ey , Ez ) e le componenti vettoriali dell’intensità (forza.) del campo magnetico (Hx , Hy , Hz ), al variare del tempo t e dello spazio (x, y, z). Esse si possono raggruppare in due terne: “la prima terna esprime la correlazione che necessariamente deve esistere nel vuoto … fra qualsiasi variazione nel tempo t di ciascuna delle tre componenti Ex , Ey , Ez della forza elettrica del campo [E] e le variazioni nello spazio delle due componenti della forza magnetica perpendicolari ad essa. Reciprocamente la seconda terna esprime l’analoga correlazione fra qualsiasi variazione nel tempo di ciascuna delle tre componenti della forze, magnetica del campo [H] e le variazioni nello spazio delle due componenti della forza elettrica ad essa perpendicolari” (bibl.81, pag.334). Si deve però notare che l’insieme delle 6 equazioni va visto come un sistema unico.

(873) Anche qui Einstein non dà semplicemente il risultato espresso dalle (14). Egli si scrive prima le (14) dipendenti da un certo fattore g(v), funzione della velocità v del sistema S’ rispetto ad S. Poi fa “l’inversione di questo sistema di equazioni, una volta per risoluzione delle equazioni appena ottenute e una seconda per applicazione delle equazioni alla trasformazione inversa (da S’ a S), che è caratterizzata dalla velocità – v”. In questo secondo caso ottiene un sistema del tipo di quello precedentemente ottenuto solo che ora è dipendente da un fattore g(-v). Poiché i due sistemi di equazioni così ottenuti debbono essere identici, deve risultare g(v).g(-v)= 1 e poi, per ragioni di simmetria, si deve avere g(v) = g(-v). Da ciò egli ricava facilmente che g(v) = 1. Anche qui quindi le equazioni di trasformazione (14) godono della proprietà di gruppo (che Einstein richiede a priori). Questo fatto ci permette di ricavare le equazioni inverse (risolte per le grandezze senza apice in funzione di quelle con apice) alle (14) con la semplice  sostituzione di –v al posto di v.

(874) Per quel che riguarda la carica, a questo punto, la si deve indicare con q’ essendo una carica nel sistema S’. Solo nel paragrafo 9 Einstein mostrerà che nel passaggio da un sistema all’altro la carica elettrica è invariante.

(875) La vecchia formulazione è per Einstein quella di. Lorentz. Egli, anche se non nomina il fisico olandese, fa esplicito riferimento in questo brano alla forza di Lorentz.

(876) Tanto più che sia la vecchia che la nuova teoria danno le stesse predizioni sperimentali  e,  nel  caso  particolare,  ammettono  il  crearsi  di  una differenza di potenziale ai capi di un conduttore sia quando quest’ultimo è mosso in un campo magnetico, sia quando è il campo magnetico che si muove rispetto al conduttore. Si veda comunque la asimmetria della quale abbiamo discusso all’inizio di questo paragrafo.

(877) Le equazioni (14) mostrano che prendere in considerazione un campo elettrico comporta, al medesimo tempo, la presa in considerazione di un campo magnetico

(878) E’ chiaro che si può fare anche il discorso per il passaggio inverso. E’ ora, invece, interessante far vedere quanto sostenuto nel testo, anche se in modo qualitativo. Consideriamo ad esempio l’equazione (14) per la componente z del campo elettrico  nel caso in cui E_z  =  0; reintroducendo la notazione 

β = (1 – v²/c²)^{– ½}, si ha:

[l’ultima relazione essendo stata ottenuta, appunto, ponendo E_z = 0]. Moltiplicando a destra e a sinistra per la carica q (abbiamo già accennato al fatto che la carica è invariante; la cosa sarà comunque vista nelle pagine seguenti) si ha:

qE’_z = (β/c)(qvH_y)

e, come si vede, nel passaggio da un sistema ad un altro, una forza elettrica (primo membro) diventa forza magnetica (di Lorentz, secondo membro).
Si noti che lo stesso Einstein, nell’intervista scritta di Shankland (già citata), ebbe modo di dire “Ciò che più o meno direttamente mi ha portato alla. teoria della relatività speciale era la convinzione che la forza elettromotrice che agisce su un corpo in moto in un campo magnetico non era altro che un campo elettrico” (bibl. 120, pag.35).

(879) Quest’ultima frase di Einstein va brevemente spiegata. Una macchina unipolare è un meccanismo schematicamente descritto in figura. Un magnete ruota intorno al suo asse zz’ mentre un circuito esterno striscia in A e B (B è il centro del magnete mentre A è nelle vicinanze di un polo; per questo il

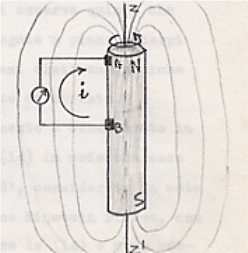
meccanismo è detto unipolare); nel circuito esterno circola una corrente i. E’ evidente, da quanto detto, che nel circuito circola corrente anche quando il magnete è immobile mentre il circuito gli gira intorno (per maggiori dettagli si veda bibl. 181, Vol. 6, pag.225). Il problema, che per primo Faraday si era posto (bibl. 71, 28ª serie, 1651), consisteva in questo: quando il magnete è in rotazione, ruotano anche le linee di forza ad esso connesse ? Einstein afferma che questo problema è privo di significato poiché non ha senso parlare di linee di forza indipendentemente dal loro stato di moto (per maggiori
dettagli si veda D’Agostino, bibl. 130, pag. 61).

(880) L’elettrone deve essere lentamente accelerato in modo che possano essere trascurate le perdite per irraggiamento di onde elettromagnetiche nello spazio.

(881) Occorre notare che Einstein non introduce la notazione f di forza.

(882) I moti relativi da noi presi in considerazione avverranno sempre per moto dell’asse x parallelo all’asse x’ (e, naturalmente, viceversa).

(883) Per lo sviluppo di questo calcolo occorre una buona conoscenza del calcolo differenziale. Per questo, con qualche dettaglio, lo sviluppo qui, in nota.

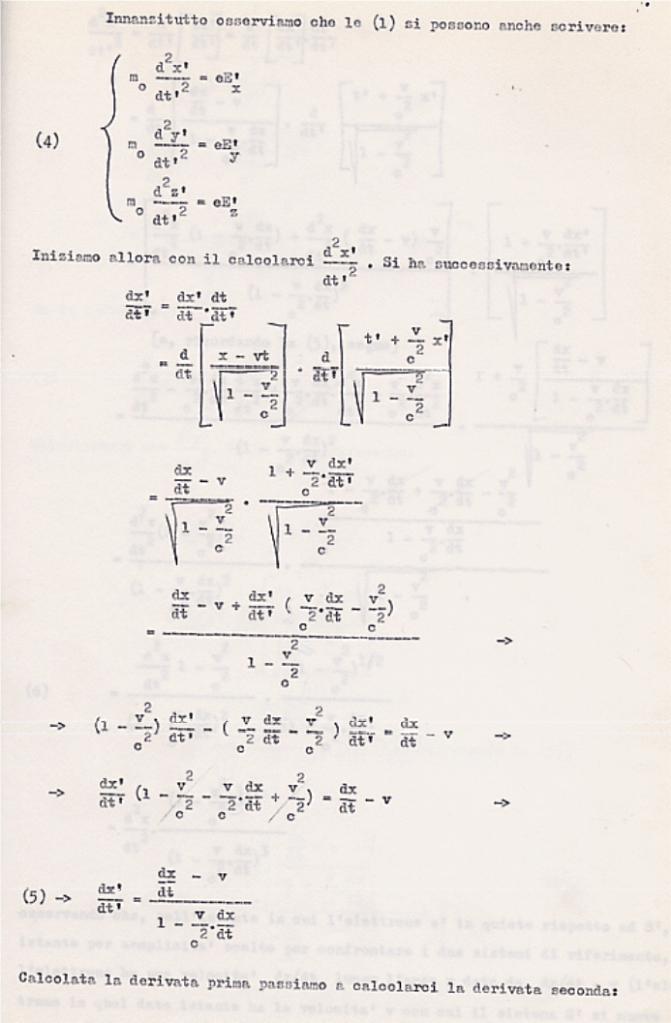
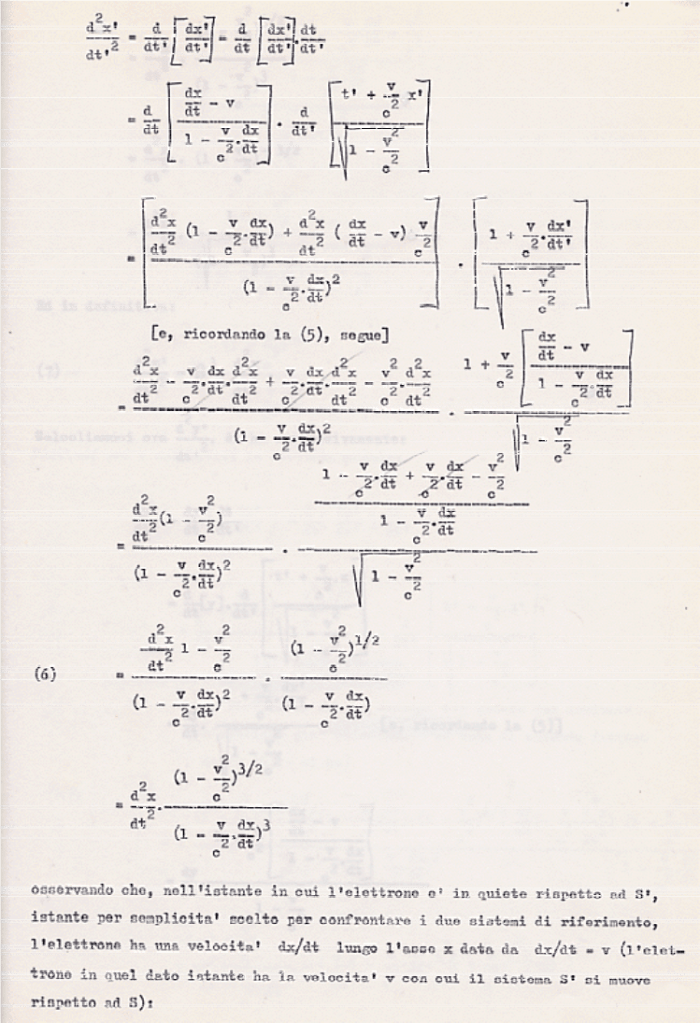
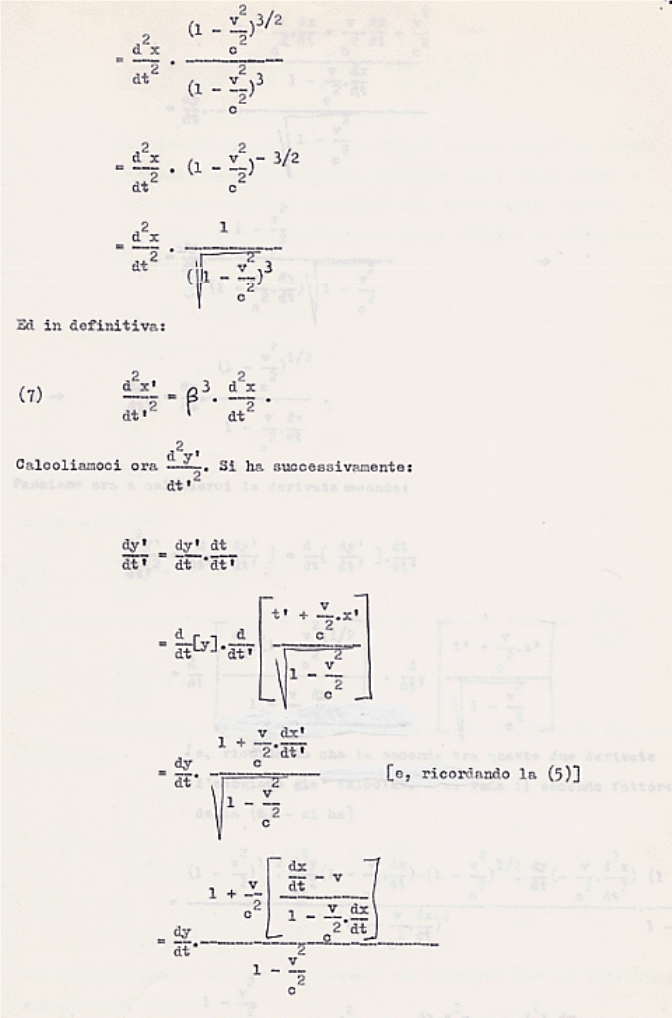
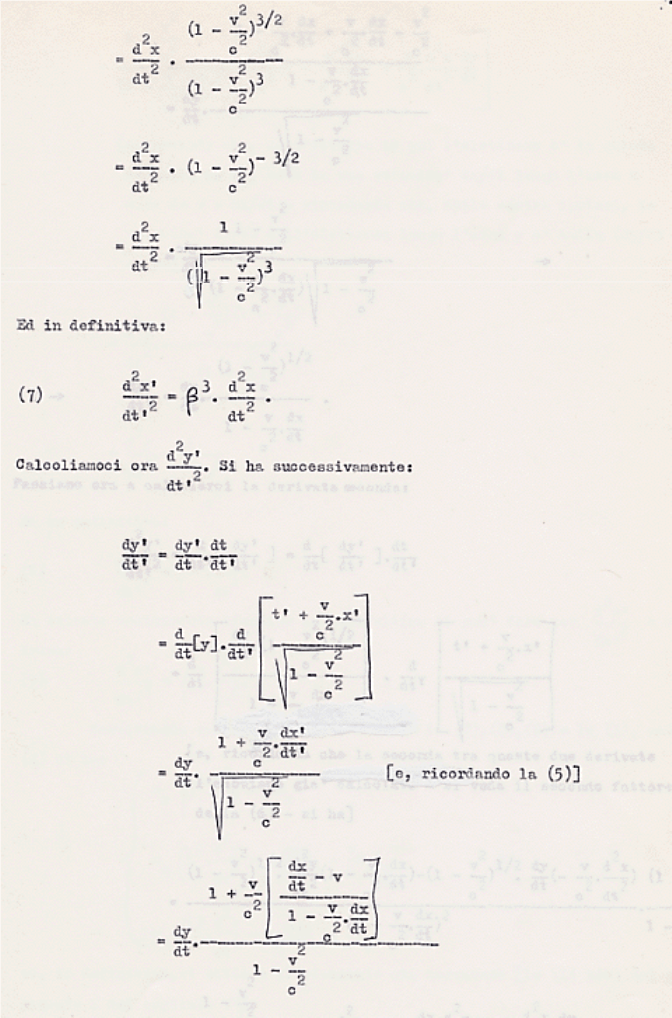
(884) Come dice Straneo in bibl. 174, pag.97. Tra l’altro Straneo osserva, riportando una considerazione di M. von Laue, che Einstein mostra qui di non conoscere la dinamica relativistica sviluppata da Lorentz nel 1904. Per la verità sulla svista di Einstein ho trovato una scarsa bibliografia. Mi è sembrato quasi che si tenda a non tener conto delle sviste di Einstein. Sarebbe utile in proposito leggersi il saggio di M. A. Tonnelat, Einstein, mito e realtà, bibl. 182.

(886) Bibl. 179, pag.l26. Ciò che dice Pauli è che bastava mantenere i secondi membri delle (15). Se si tiene infatti conto di quanto fin qui detto, le equazioni del moto di una particella carica in un campo elettromagnetico sono date dall’equazione:

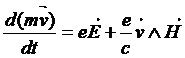
(1)
dove al primo membro si ha la forza con cui il campo elettrico agisce sulla carica, mentre al secondo membro si ha la forza di Lorentz. Per vedere come le (15) sono l’espressione qui data, si segua il seguente calcolo.
Ricordiamo innanzitutto l’espressione che ci fornisce il prodotto vettoriale ( Λ) tra due vettori A e B. Si ha:

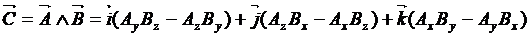
(2)

dove i, j, k sono dei vettori unitari (o versori); le quantità tra parentesi sonole componenti del vettore risultante, rispettivamente, lungo gli assi x, y, z; le A_x, A_y, A_z, B_x, B_y, B_z  sono le componenti dei vettori  e   lungo gli assi indicati dai bubindici.

            Sviluppando il secondo membro della (1) secondo le (2), si ha (ricordando che, nel secondo passaggio, abbiamo posto v_y = v_z = 0 e che, più oltre, la velocità lungo l’asse x è semplicemente indicata con v):

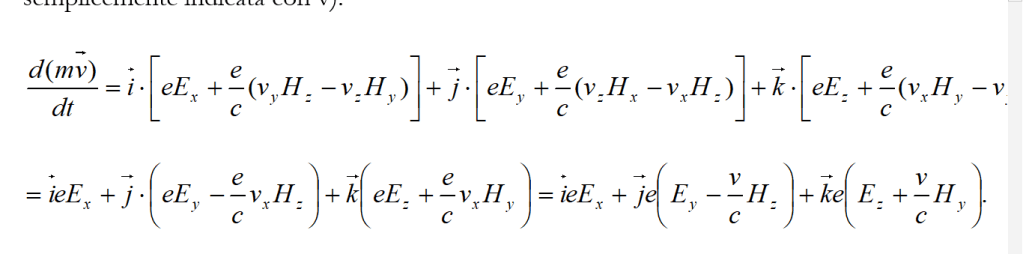
Confrontando con la (15) si può subito vedere che la somma di queste tre ultime quantità non è altro che la somma dei secondi membri delle (15) e ciò mostra quanto ci eravamo proposti.

(887) Ho detto in gran parte poiché anche Planck, in un primo tempo, non riuscì a scrollarsi di dosso completamente la formulazione newtoniana della meccanica Le maggiori difficoltà nascevano soprattutto dal simbolismo. Fu Minkowski che nel 1908 avviò tutti i problemi a soluzione.

(888) M. Plance: II principio di relatività e le equazioni fondamentali della meccanica, Verh. Dtsh. Phys. Ges., 4, 1906, pagg. l36-141. Per seguire nelle sue linee essenziali questo lavoro si può vedere bibl .112, Vol.2, pagg.44-48.

(889) Citato da Straneo (bibl .174, pag. 97). Si noti che per teorema dell’impulso si intende ciò che abbiamo detto sulla quantità di moto, mentre per quel che riguarda il teorema dell’energia ci si riferisce alla conservazione dell’energia, tema che Einstein affronterà subito dopo quello che stiamo discutendo.

(890) Si veda la nota 6 a pag. 63 di bibl. 131.

(890 bis) Si noti con quali semplici parole Einstein passa a generalizzare quanto trovato per gli elettroni alle particelle materiali di qualunque tipo. Si osservi inoltre che Einstein assume per l’elettrone a riposo la forma sferica senza porsi i problemi che si erano posti Lorentz ed. Abraham a proposito del suo essere soggetto a disintegrarsi a seguito della repulsione elettrostatica delle cariche negative elementari che lo avrebbero dovuto costituire.

(891) L’integrale proposto si risolve nel modo seguente:

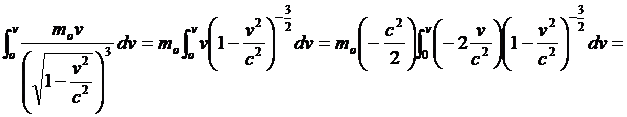
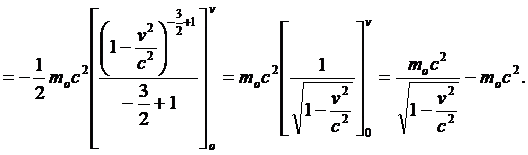
Come si può vedere, questo è il risultato che abbiamo dato nella (22) del paragrafo 2 del capitolo V.

(888) M. Plance: II principio di relatività e le equazioni fondamentali della meccanica, Verh. Dtsh. Phys. Ges., 4, 1906, pagg. l36-141. Per seguire nelle sue linee essenziali questo lavoro si può vedere bibl .112, Vol.2, pagg.44-48.

(889) Citato da Straneo (bibl .174, pag. 97). Si noti che per teorema dell’impulso si intende ciò che abbiamo detto sulla quantità di moto, mentre per quel che riguarda il teorema dell’energia ci si riferisce alla conservazione dell’energia, tema che Einstein affronterà subito dopo quello che stiamo discutendo.

(890) Si veda la nota 6 a pag. 63 di bibl. 131.

(890 bis) Si noti con quali semplici parole Einstein passa a generalizzare quanto trovato per gli elettroni alle particelle materiali di qualunque tipo. Si osservi inoltre che Einstein assume per l’elettrone a riposo la forma sferica senza porsi i problemi che si erano posti Lorentz ed. Abraham a proposito del suo essere soggetto a disintegrarsi a seguito della repulsione elettrostatica delle cariche negative elementari che lo avrebbero dovuto costituire.

(891) L’integrale proposto si risolve nel modo seguente:

Come si può vedere, questo è il risultato che abbiamo dato nella (22) del paragrafo 2 del capitolo V.

Categorie:Senza categoria