Ingegneria Meccanica – Roma Tre

AA/2011-2012

APPUNTI PER IL CORSO

(Ripresi integralmente e da me assemblati dai testi di bibliografia)

Roberto Renzetti

Bibliografia: R. Renzetti –Vari appunti miei raccolti negli anni -www.fisicamente.blog

LA DILATAZIONE DEI TEMPI

         Riferiamoci alla figura 50 che, per comodità, riporto

FIGURA 50

e supponiamo che sul sistema  S abbia luogo un fenomeno (l’oscillazione di un pendolo, una scarica elettrica, la caduta di un grave, …) della durata Δt  = t₂ – t₁ .

        Utilizzando le equazioni di trasformazione di Lorentz (8), ci domandiamo qual è la durata Δt’ = t’₂  – t’₁ dello stesso fenomeno misurato da T’ in S’. Si ha:

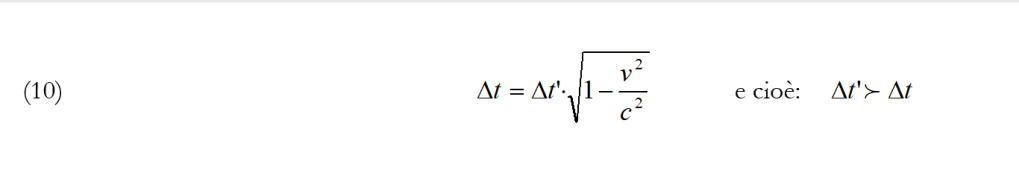
e ciò vuol dire che, per l’osservatore T’, la durata Δt’ del fenomeno risulta minore [si ricordi che 0 ≤ (1 – v²/c²)^1/2 ≤ 1] della durata Δt misurata, per lo stesso fenomeno, dall’osservatore T (in quiete rispetto al «fenomeno»): per T’ il tempo passa più lentamente (le oscillazioni di un pendolo che abbiano la durata di 10 sec se misurate da S – nel caso in cui v valga 180.000 Km/sec – avranno una durata di 8 sec se misurate da S’).

        Non è ozioso andare a vedere il problema reciproco.

        Supponiamo ora che sul sistema S’ abbia luogo un fenomeno della durata Δt’ = t’₂ – t’₁. Utilizzando le trasformazioni di Lorentz (8), qual è la durata  Δt  =  t₂ – t₁ dello stesso fenomeno misurato in S ? Si ha:

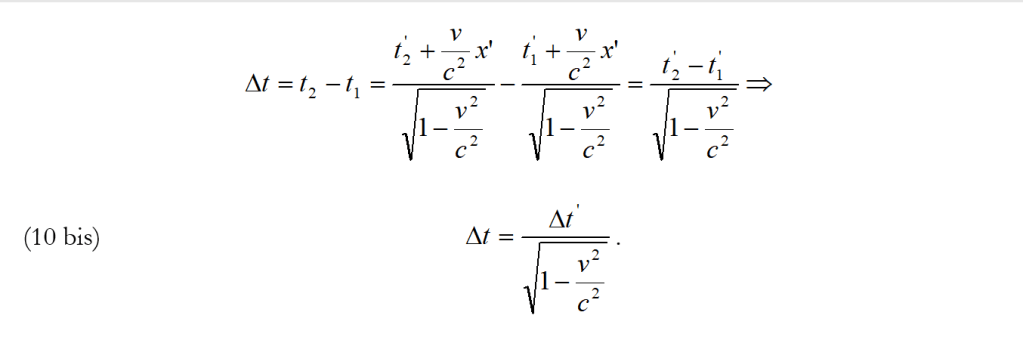
[si confronti questa espressione con la (l)].

         Quindi l’osservatore T, che si trova su S, misurerà una stessa dilatazione del tempo ma, questa volta, sul sistema S’ E questo fatto è in completo accordo con il principio di relatività; ad esso si poteva arrivare semplicemente sostituendo a Δt’, Δt, v della (9) rispettivamente le quantità Δt, Δt’, -v.

         E qui sta la non oziosità di questo breve calcolo. Non bisogna utilizzare la (9) o la (10 bis) per misure effettuate una volta dall’uno e una volta dall’altro riferimento, semplicemente ricavandosi, a partire da una sola delle espressioni suddette, Δt o Δt’, a seconda delle necessità: ciò porterebbe a risultati erronei assegnando un valore assoluto alla dilatazione del tempo (ritorneremo su questo argomento quando ci occuperemo del paradosso dei gemelli).

         Per concludere questo argomento occorre dire che l’intervallo di tempo esistente tra due eventi successivi che accadono nello stesso luogo di un dato riferimento, quando è misurato nello stesso riferimento, è chiamato tempo proprio. Il tempo proprio risulta quindi essere l’intervallo di tempo più breve esistente tra due eventi successivi che avvengono in un dato riferimento; lo stesso intervallo di tempo, misurato da qualunque altro riferimento in moto rispetto a quello dato, risulterà maggiore (dilatazione del tempo).

LA CONTRAZIONE DELLE LUNGHEZZE

        Ancora riferendoci alla figura 50, supponiamo di considerare un’asta rigida situata in quiete nel sistema S’. Su quel sistema essa verrà misurata a riposo con un regolo che faccia coincidere simultaneamente i suoi estremi con quelli dell’asta.

        La lunghezza dell’asta misurata in S’ sia ℓ’ =  x’₂ – x’₁. Poiché gli estremi di quest’asta sono ivi misurati simultaneamente, si avrà t’₁ = t’₂ (dove t’₁ rappresenta l’istante in cui un estremo del regolo è fatto coincidere con un estremo dell’asta e t’₂ l’istante in cui l’altro estremo del regolo è fatto coincidere con l’altro estremo dell’asta).

         Analogamente, quando quest’asta viene misurata in riposo nel sistema S (valgono anche qui le considerazioni sulla simultaneità per cui si ha t₁  = t₂), essa sarà lunga ℓ = x₂ – x₁.

        Se i due sistemi fossero in quiete relativa si avrebbe subito  ℓ = ℓ’. Ma poiché i due sistemi sono in moto relativo con velocità v, l’osservatore che si trova in S, utilizzando le trasformazioni di Lorentz (8), troverà per l’asta la lunghezza:

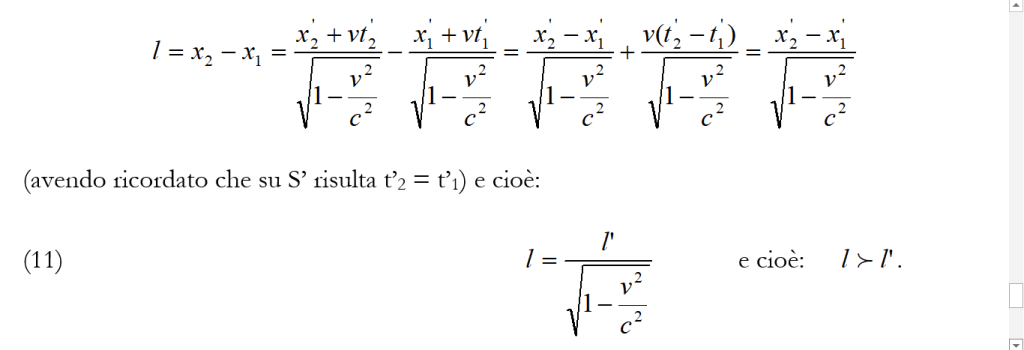
[si confronti questa espressione con la (2)].

         In definitiva, un osservatore che veda un’asta in movimento le attribuisce una lunghezza inferiore di quella che risulterebbe da una misura effettuata da un osservatore in quiete rispetto all’asta stessa.

        Anche qui vale la perfetta reciprocità: se l’asta rigida fosse situata a riposo nel sistema S e fosse osservata da S’ essa, per l’osservatore che si trova su S’, risulterebbe contratta.

        Per concludere questo argomento, anche qui, occorre dire che la lunghezza di un dato oggetto, misurata nel riferimento in cui l’oggetto è in quiete, è chiamata lunghezza propria dell’oggetto. La stessa lunghezza misurata da un riferimento in moto rispetto al riferimento in cui l’oggetto è in quiete, risulterà più piccola. Ciò vuol dire che la lunghezza propria è la lunghezza più lunga che possa essere misurata per un dato oggetto.

Categorie:Senza categoria