Ingegneria Meccanica – Roma Tre

AA/2011-2012

APPUNTI PER IL CORSO

(Ripresi integralmente e da me assemblati dai testi di bibliografia)

Roberto Renzetti

Bibliografia: R. Renzetti –Vari appunti miei raccolti negli anni -www.fisicamente.blog

EQUAZIONI DI TRASFORMAZIONE RELATIVISTICHE.

L’EQUAZIONE FONDAMENTALE DELLA DINAMICA RELATIVISTICA

        Riprendiamo in esame una relazione già incontrata, la (l5):

che si può anche scrivere:

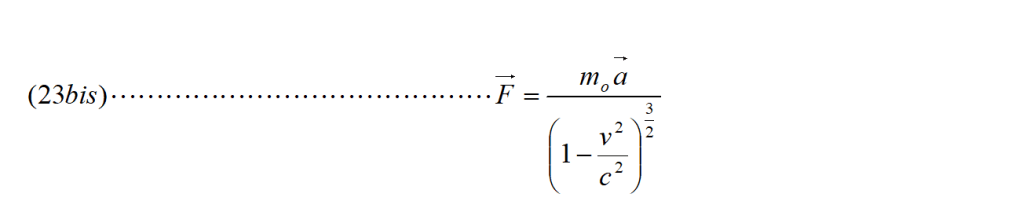
avendo posto dv/dt = a.

        Ma, nel caso più generale, quando forza, accelerazione e velocità non sono più vettori tra loro paralleli, come si sviluppa la (15) ? Ricordando che p = mv e che sia m che v sono grandezze variabili, la (15) diventa (si tratta di far la derivata di un prodotto tra due funzioni):

Ed allora per dm/dt si ha:

(dove α è l’angolo fra le direzioni di F e ds) cioè che l’energia cinetica elementare dE_c è data dal prodotto scalare (x) della forza F per lo spostamento elementare ds; la precedente relazione si può anche scrivere:

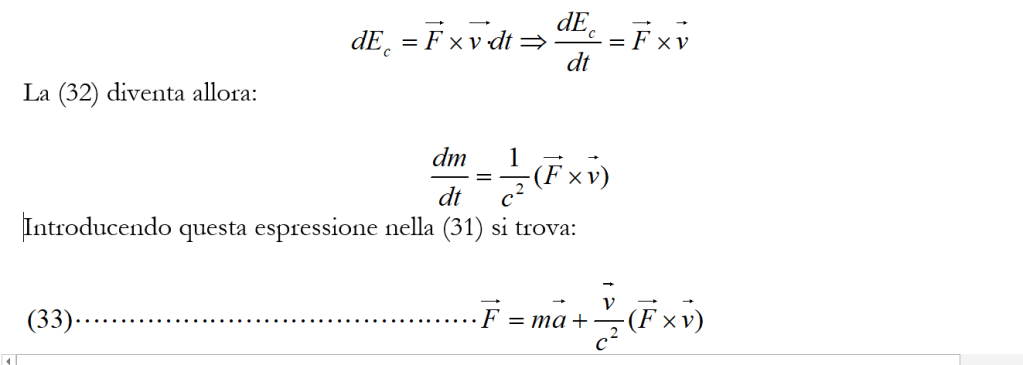
che è l’equazione fondamentale della dinamica relativistica.

        La (33) si può anche scrivere:

Si può subito vedere che l’accelerazione e la forza non hanno, in generale, la stessa direzione (si veda figura 69) poiché ad F occorre sommare il vettore-secondo-termine-del-secondo-membro che non ha necessariamente la direzione di F (questo fatto non si verificava in dinamica classica). Inoltre, sempre

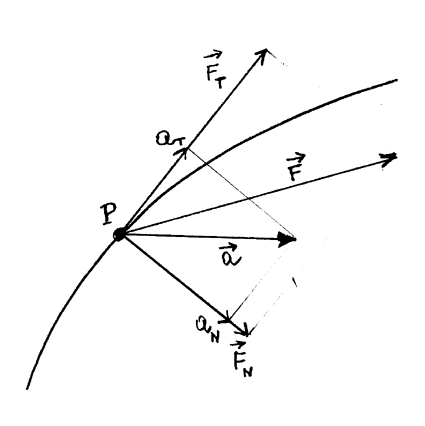
Figura 69

dalla figura 69 si può vedere che invece le componenti tangenziali a_T  e F_T  della forza e dell’accelerazione e le componenti normali a_N  e F_N sempre della forza e dell’accelerazione hanno rispettivamente stessa direzione e stesso verso (si noti che risulta sempre F_T  > F_N).

        Indaghiamo un poco meglio le componenti tangenziale e normale della forza F (rispettivamente F_T  ed F_N) riprendendo in esame la (31):

essere interpretata come la massa che si ottiene per un moto rettilineo, e cioè una massa longitudinale m_L . Si può allora scrivere la (23) nel modo seguente:

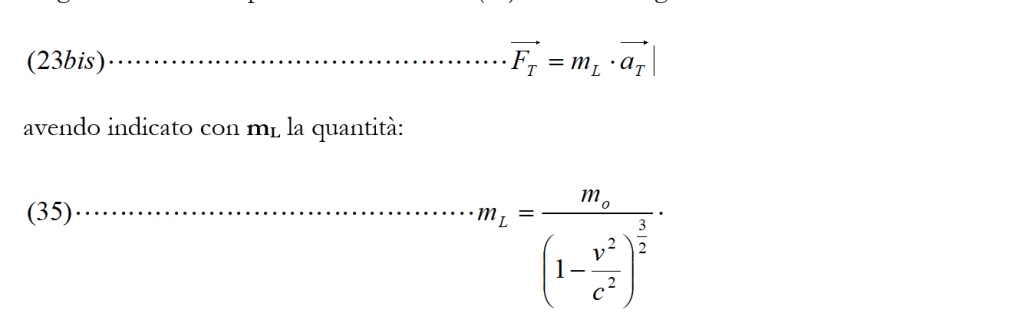
        Nel caso invece in cui la forza  F che compare nella (33) risulti perpendicolare alla velocità v, la stessa forza  risulterà parallela all’accelerazione a. Questo perché quando forza e velocità sono perpendicolari formano tra loro un angolo α di 90°; se α è di 90° ai avrà che cos α = 0 ; e se cos α = 0 il secondo termine del secondo membro della (33 bis) si

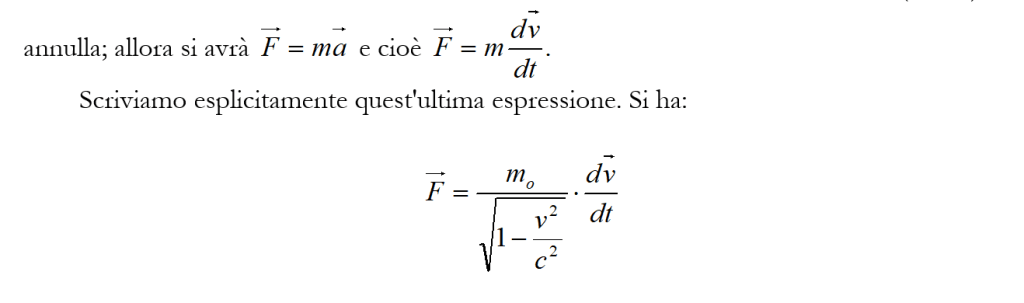
Date le nostre premesse di perpendicolarità esistente tra velocità da una parte e forza ed accelerazione dall’altra, si avrà, in analogia con quanto visto per la (23 bis) e la (35):

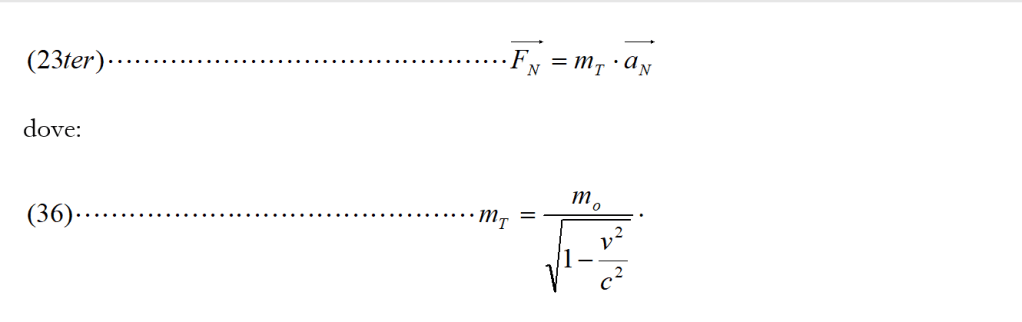
rappresenta quella che va sotto il nome di massa trasversale (al movimento).

Categorie:Senza categoria