Ingegneria Meccanica – Roma Tre

AA/2011-2012

APPUNTI PER IL CORSO

(Ripresi integralmente e da me assemblati dai testi di bibliografia)

Roberto Renzetti

Bibliografia: R. Renzetti –Vari appunti miei raccolti negli anni -www.fisicamente.blog

LE EQUAZIONI DI TRASFORMAZIONE PER LA MASSA E PER LA FORZA

            Le equazioni di trasformazione per la massa, sempre rispetto ai riferimenti S ed S’ presi in considerazione nella sezione precedente, si possono ricavare facilmente a partire da uno dei passaggi che abbiamo incontrato per ricavare la (39):

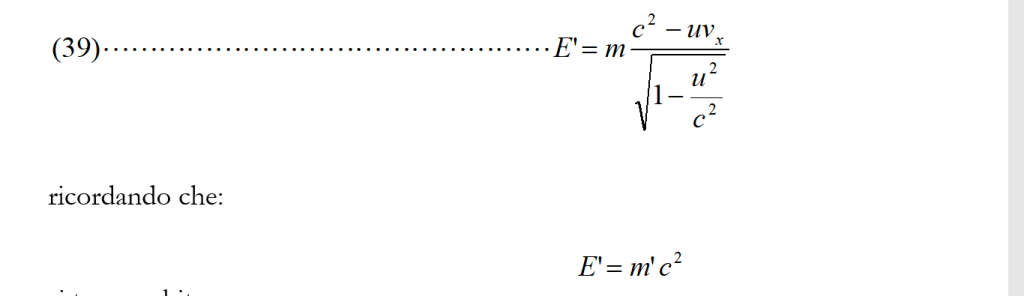
si trova subito:

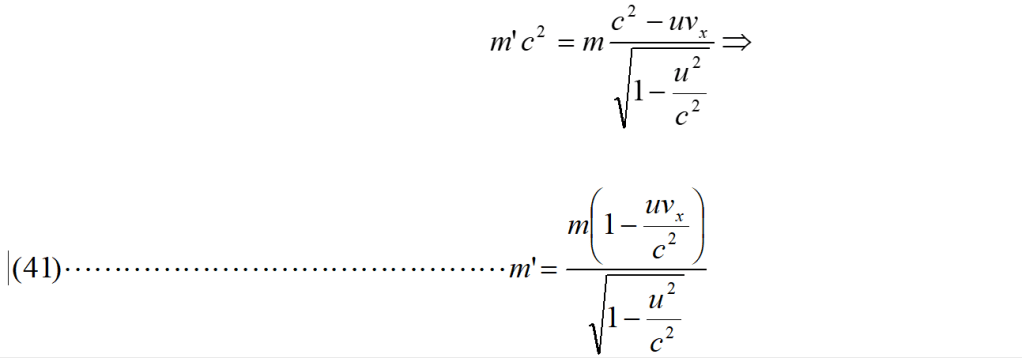
Per il principio di relatività e sostituendo –u ad u, si ricava:

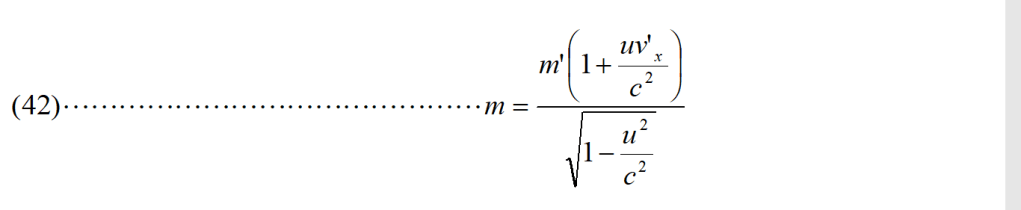
E la (41) e (42) sono le equazioni di trasformazione per la massa da noi cercate.

            Per quel che riguarda le equazioni di trasformazione della forza, basta ricordare la definizione (15):

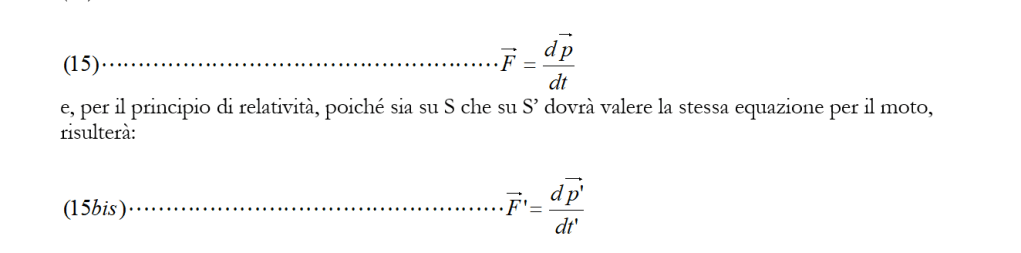
Il problema può allora essere risolto utilizzando le (40). Tenendo conto delle componenti F_x, F_y ed F_z della forza F e ricordando la trasformazione di Lorentz (8) per t’, si ha:

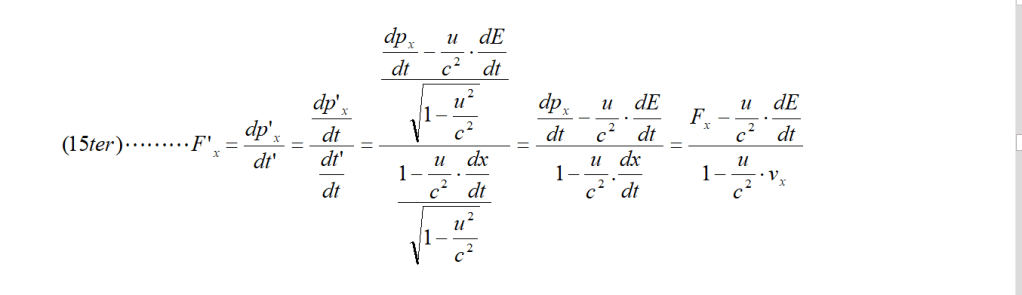
avendo posto v_x =  dx/dt.

            Resta da calcolare dE/dt. Lo faremo semplificando il problema con l’ipotesi che l’oggetto su cui agisce la forza sia istantaneamente in quiete su S’ (v’ = 0). Ricordando la (21 bis):

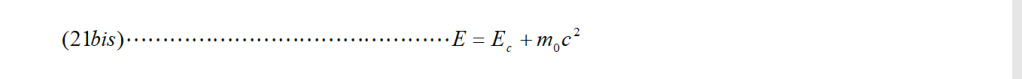
che la variazione infinitesima dell’energia cinetica (dE_c) è uguale al lavoro infinitesimo (F_x.dx) e che m₀c²  è una costante, si ha:

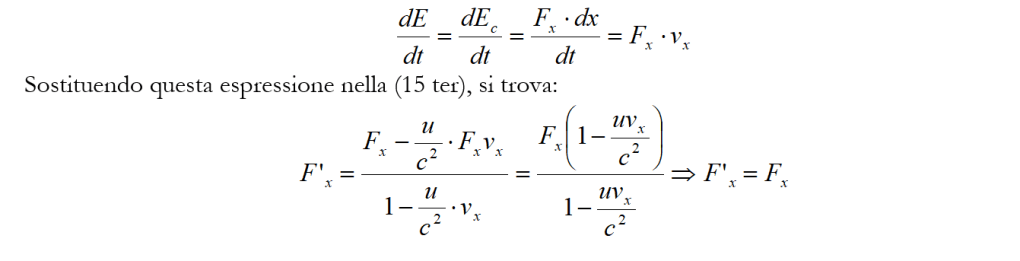
In modo più semplice si può procedere per F’_y ed F’_z. Sempre ricordando le (40) e la seconda delle (10), e cioè  dt/dt’ = 1/(1 – u²/c²)^1/2, si ha:

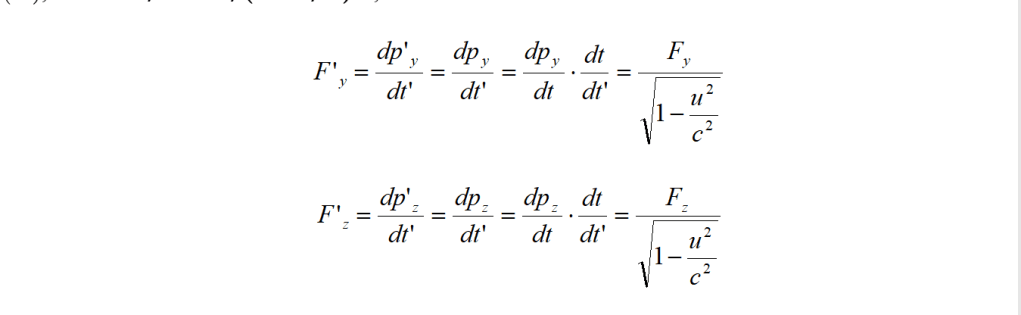
Ricapitolando, nel caso particolare in cui l’oggetto su cui agisce la forza sia in quiete su S’ ad un dato istante (istante nel quale v’ = 0), le equazioni di trasformazione per la forza sono:

Nel caso più generale, in cui l’oggetto su S’ sia già dotato di una data velocità (v’ ≠  0) quando su di esso agisce la forza, si può dimostrare che valgono le seguenti equazioni di trasformazione (si veda, ad esempio, A. P. French – Special Relativity – Norton & Co., New York, 1968):

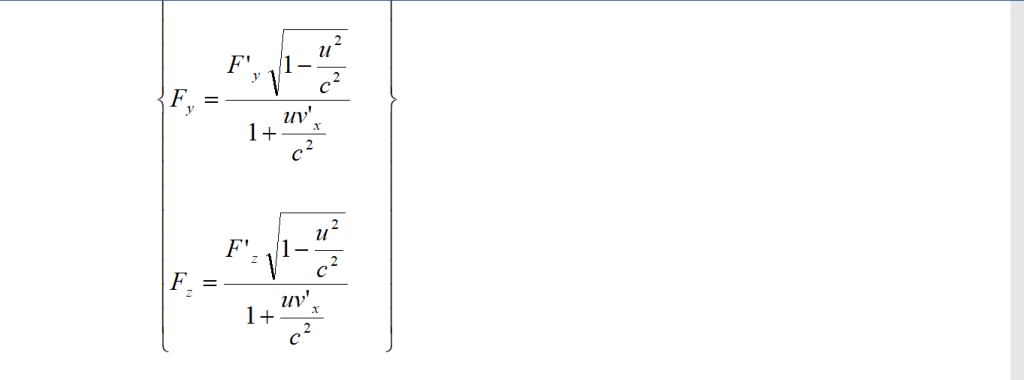
Categorie:Senza categoria