PARTE II
Roberto Renzetti
2.1 – COSA SI CONSERVA, mv o mv2 ?
Abbiamo già visto che Huygens iniziò con grande ammirazione per Descartes. Poi riconobbe che era stata la sua gioventù a portarlo fuori strada e che le elaborazioni di Descartes, particolarmente per ciò che riguardava la conservazione della quantità di movimento, gli risultavano in alcun modo sostenibili. Da qui egli iniziò ad elaborare una teoria alternativa che, come suo solito, era accompagnata da abbondante sperimentazione. Alla fine dei suoi lavori pubblicò un trattato in 13 Proposizioni, De motu corporum ex percussione(1) (pronto nel 1667 ma pubblicato postumo nel 1703), in cui erano raccolti tutti i risultati delle sue elaborazioni teoriche e sperimentali sui problemi d’urto tra corpi (oggi diremmo masse) perfettamente duri (oggi diremmo perfettamente elastici).
Dice Westfall:
Huygens dimostrò l’errore di Cartesio sulla base degli stessi principi
cartesiani. Per Cartesio, quiete e moto erano termini relativi; non esistendo spazio alcuno salvo i corpi, si può solamente dire che un corpo si muove o rimane fermo in rapporto ad un altro corpo. Le sue regole sull’urto purtroppo davano risultati diversi a seconda dei presupposti teorici. Un corpo minore in moto rimbalza da uno maggiore in quiete mantenendo intatta la sua velocità, mentre il corpo maggiore non subisce cambiamenti di sorta.
Cambiando però i presupposti teorici e considerando il corpo minore in
quiete, quello maggiore lo mette in moto, perdendo tanto moto quanto ne dà al corpo minore, e dopo l’urto i due corpi si muovono insieme. Ovviamente il secondo risultato non concorda con il primo se moto e quiete sono termini relativi, come voleva Cartesio. Huygens accettò la relatività del moto [anche se Huygens ebbe a scrivere – Oeuvres completes, Vol. VI, pag. 213 -, a proposito della contrapposizione di moto assoluto con moto relativo: Non è un argomento matematico difficile, ma fisico, iperfisico …; ndr]. Il problema era allora di rivedere le regole dell’urto.
A questo fine, immaginò un esperimento teorico quale soltanto un olandese avrebbe potuto pensare(2). Una barca costeggia tranquillamente un tranquillo canale olandese, e sulla barca un uomo compie esperimenti sull’urto tra i corpi. Huygens immagina i corpi sospesi a corde che l’uomo tiene in mano; congiungendo le mani, fa cozzare i corpi tra loro. Tutto ciò naturalmente va inteso come il tentativo di eliminare anomalie come la frizione e di realizzare il moto ideale di Galileo. Le corde hanno il vantaggio di permettergli di mettere a riva un secondo uomo che stringe le mani al primo quando passa la barca. Due uomini insieme svolgono il medesimo esperimento.
Per sviluppare i suoi ragionamenti, Huygens parte da alcune assunzioni di grande rilievo [per questo argomento mi rifaccio a Mach]. Si afferma il principio d’inerzia enunciato così:
- Un corpo mosso continua a muoversi, se non ha impedimenti, con la stessa velocità costante e lungo una linea retta
e quindi si danno per buone le seguenti regole:
2 – I corpi elastici che abbiano massa uguale, quando si urtano con velocità uguali ed opposte acquistano, dopo l’urto, le stesse velocità che avevano prima ma in verso opposto
3 – Tutte le velocità sono da considerarsi come relative
4 – Quando un corpo più grande ne urta uno più piccolo che è in quiete gli comunica parte della sua velocità
5 – Se uno di due corpi che si urtano conserva la propria velocità, anche
l’altro la conserva.
Dopo queste ipotesi si iniziano a discutere le differenti possibilità di urto. Per discutere il tutto, in termini relativistici, Huygens discute le sue esperienze da due punti di osservazione, quello di chi si trova sulla barca in moto con velocità v e quello di chi si trova sulla riva. Le esperienze consistono in urti di pendoli, sostenuti dai due osservatori. Ciascun osservatore fa la medesima esperienza. Vediamo le più significative cose che Huygens discute.

La figura che compare nella Prima pagina del De motu corporum ex percussione
Huygens inizia nella Proposizione I a discutere di un corpo fermo urtato da un altro corpo uguale. Egli mostra che, dopo l’urto, il corpo che era in moto resterà fermo mentre il corpo che era fermo acquisterà la velocità che aveva il corpo in moto. Nella Proposizione II egli passa a discutere l’ipotesi 2, tenendo conto della 3, facendo anche qui riferimento alla figura, riprodotta più in alto, che compare nella prima pagina del De motu … . Egli immagina, come accennato, che il fenomeno in discussione abbia luogo su una barca in movimento con velocità v, barca che Mach schematizza con il disegno seguente:
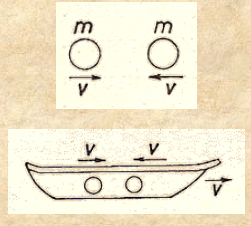
Si hanno così due osservatori per lo stesso fenomeno, quello fermo a terra e quello in moto con velocità v sulla barca. Per colui che si trova sulla barca il fenomeno va così come è descritto nel punto 2; per colui che si trova invece a terra le velocità dei due corpi sono, prima dell’urto, rispettivamente 2v e 0 e, dopo l’urto, 0 e 2v. Per colui che si trova a terra a descrivere tale urto elastico, accade che: un corpo che ne urti uno immobile ed uguale(3) gli comunica tutta la sua velocità restando in quiete dopo l’urto. Più in generale accade che la barca abbia una velocità qualunque u. In tal caso le velocità per l’osservatore a terra sono, prima dell’urto, u + v ed u – v e, dopo l’urto, u – v ed u + v. Da ciò si conclude facilmente che corpi elastici uguali si scambiano nell’urto la loro velocità. Agendo sulla velocità della barca, Huygens fu in grado di esaminare tutti i casi che comportavano corpi uguali. Per affrontare corpi diversi, ipotizzò anche che, ogni qual volta un corpo ne colpisce uno più piccolo fermo, lo mette in moto e perde quella parte del moto che trasferisce al corpo più piccolo. Mediante la barca, aveva rovesciato lo stato di quiete e di moto. Sulla base dei nuovi presupposti teorici, il moto perduto dal corpo grande per muovere quello piccolo appare come moto comunicato a quello grande dall’urto del corpo piccolo. La questione è affrontata nella Proposizione III, sempre tenendo conto dell’ipotesi 3, prendendo le mosse su una strada aperta da Galileo.
Un corpo in quiete, per quanto grande, è messo in moto da un corpo più piccolo che lo urta ed Huygens mostra che l’avvicinamento dei corpi prima dell’urto e l’allontanamento dopo l’urto avvengono con la stessa velocità relativa. Seguiamo Mach:
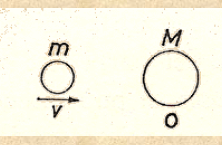
Un corpo m urta contro un altro in quiete di massa M (vedi figura), al quale nell’urto comunica la velocità w, non determinata. Per dimostrare il suo teorema Huygens suppone che il fenomeno abbia luogo su una barca che si muove da M verso m con la velocità w/2. Le velocità iniziali sono dunque v, – w/2, – w/2, le velocità finali x, + w/2. Poiché M non muta il valore della velocità ma solo il segno, anche m, se non ha perduto forza viva nell’urto elastico, cambia soltanto il segno della sua velocità. Di conseguenza levelocità finali sono – (v – w/2), + w/2, cioè la velocità relativa di avvicinamento prima dell’urto è uguale alla velocità relativa di allontanamento dopo l’urto. Qualunque sia il cambiamento di velocità, sempre, come in questo esempio della barca, il valore della velocità prima e dopo l’urto non cambia se non tiene conto dei segni. Il teorema acquista così valore generale.
A questo punto è indispensabile un’osservazione. Huygens introduce il teorema delle forze vive solo nella Proposizione XI ma lo usa già a partire dalla Proposizione VIII. Il fatto si spiega nella logica della cronologia di redazione delle sue opere. Infatti il teorema delle forze vive era stato ricavato da Huygens in relazione al moto pendolare che aveva studiato a partire dal 1657 e questo lavoro sugli urti, anche se pubblicato postumo nel 1703, era stato redatto nel 1667. E’ plausibile che, nella redazione del De motu, Huygens applicasse cose che dava per scontate in quanto già ricavate in Lavori diversi di statica e dinamica del 1661(5). Fatta questa premessa, passo ad occuparmi della Proposizione VIII che, come detto, introduce l’applicazione del teorema delle forze vive, per passare subito dopo ad illustrare il modo con cui Huygens ricava quest’ultimo teorema. Continuo con Mach:
Se due masse M e m si urtano con la velocità V e v inversamente proporzionali alle masse, M rimbalza dopo l’urto con velocità V e m con velocità v. Supponiamo che le velocità dopo l’urto siano V1 e v1; in base al precedente teorema abbiamo V + v = V1 + v1, e per il teorema delle forze vive:
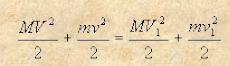
Supponiamo che V1 = v + w; allora necessariamente V1 = V – w; in questo caso la somma sarà:
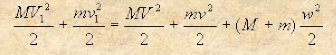
Questa uguaglianza può essere valida solo se si pone w = 0, e con ciò il teorema sopra esposto è dimostrato. Huygens ha raggiunto la prova mediante il confronto, compiuto con l’aiuto di una costruzione geometrica, fra le altezze a cui possono salire i corpi prima e dopo l’urto. Se le velocità dei corpi che si urtano non sono inversamente proporzionali alle masse, si può ottenere questo diverso rapporto immaginando un conveniente movimento della barca. Il teorema allora include ogni caso possibile.(4)
In questo modo, studiando ogni possibilità relativa a corpi elastici, Huygens fornisce tutte le leggi degli urti con una completa trattazione relativistica. Questi importanti risultati saranno ripresi da Newton e resi in forma più moderna e comprensibile al nostro modo di affrontare tali problemi, tra l’altro, con l’introduzione accennata della massa.
Per ciò che abbiamo potuto vedere, a fianco della grandezza mv che conosciamo come quantità di moto, abbiamo introdotto la grandezza mv2 che è invece una energia (anche se tale nome non era ancora utilizzato) chiamata forza viva. La comparsa di quest’ultima grandezza fece nascere un lungo dibattito tra coloro che si erano messi sulla linea di Descartes e Gottfried Wilhelm Leibniz (1646–1716). Il dibattito, che verteva su quale delle due grandezze si conservasse e che ebbe anche sviluppi in ambito di premi banditi su tale argomento, si protrasse per tutto il XVIII secolo, quando fu ancora ripreso da Pierluigi Lagrange (1736–1813) nella sua Mécanique analytique del 1788. Il problema comunque andava al di là della mera scelta di cosa si conservasse. L’argomento è troppo lungo da trattare ed esula dai fini di questo lavoro ma chi è interessato potrà leggere qui l’evoluzione della questione. Invece riporto ora il nocciolo del problema della conservazione delle due grandezze, come riportato da Mach ed alcune altre considerazioni:
La somma delle quantità di moto di un corpo in movimento si conserva
nell’urto, tanto se i corpi sono elastici quanto se non lo sono. Bisogna però intendere qui la conservazione in un senso diverso da quello che le diede Descartes. Nell’urto la quantità di moto di un corpo non diminuisce in proporzione a quella che aumenta in un altro corpo. Quando, per esempio, due masse uguali anelastiche si urtano con velocità uguali e opposte, perdono entrambe la loro quantità di moto intesa in senso cartesiano. Al contrario la somma di queste quantità si conserva se si dà segno positivo a tutte le velocità che hanno una direzione e segno negativo a quelle didirezione opposta. La quantità di moto così concepita resta costante in tutti i casi.
La somma delle forze vive di un sistema di masse varia nell’urto se si tratta di masse anelastiche; invece si conserva per le masse perfettamente elastiche. È possibile misurare la diminuzione delle forze vive che si determina nell’urto di masse anelastiche, o, in generale, quando i corpi si muovono dopo l’urto con velocità comune. […] La perdita di forza viva nell’urto è equivalente al lavoro prodotto dalle forze interne, cioè dalle cosiddette forze molecolari.
La disputa quindi non poteva avere vincitori. Sarà necessario attendere gli sviluppi della Termodinamica e l’affermazione del Primo Principio di essa.
Vi è comunque un dato da registrare. Nel 1692 Huygens scriveva a Leibniz a proposito di suoi articoli inviati alla Royal Society affermando che
in essi ho fatto uso, tra l’altro, di questa conservatio virium aequalium, e
della deduzione del moto perpetuo, vale a dire dell’impossibile [Oeuvres
completes, Vol. X, pag 303]
Inoltre, nel caso di collisioni perfettamente elastiche, egli aveva dimostrato in due articoli al Journal des Sçavants e nelle Philosophical Transactions of Royal Society (ambedue scritti nel 1686 e pubblicati postumi nel 1699) che la somma dei prodotti delle masse e dei quadrati delle rispettive velocità, calcolata prima dell’urto, è uguale all’espressione corrispondente calcolata dopo l’urto. Questo teorema si era presentato anche a Leibniz sempre nel 1686. Di esso aveva scritto ad Huygens preparando anche un articolo pubblicato nel 1686 negli Acta eruditorum dal titolo Demonstratio erroris memorabilis Cartesii. E’ in tale articolo che Leibniz chiama forza viva il prodotto di una massa per il quadrato della sua velocità (quasi quella che noi chiamiamo energia cinetica; diventerà proprio l’energia cinetica quando Coriolis – 1792-1843 – introdurrà per essa il fattore moltiplicativo 1/2) mentre chiama forza morta la stessa cosa che non è in moto, quella che noi chiamiamo oggi energia potenziale. A tal proposito dice Gliozzi (in Abbagnano):
Ora, Leibniz proponeva di valutare la « forza » (noi diremmo l’energia) di
un corpo in caduta libera dall’altezza alla quale questo corpo potrebbe
risalire, se fosse rilanciato verso l’alto con la velocità acquisita, sicché si
avrebbe in ogni caso eguaglianza tra forza viva e forza morta. Se la «forza» si valuta così, dalle leggi della meccanica risulta che essa è eguale al prodotto del «corpo» per il quadrato della sua velocità, sicché un corpo dotato di velocità doppia possiede una «forza» quadrupla. Ciò che si conserverebbe nell’urto dei corpi non è la quantità di moto, come affermava la terza regola di Descartes, ma la somma delle forze vive dei corpi urtanti: è questo, secondo Leibniz, l’errore di Cartesio.
Ma i cartesiani si levarono contro Leibniz in difesa di Descartes … [Essi]
facevano osservare che i corpi rilanciati verso l’alto risalivano alla stessa
altezza in un tempo doppio e produrre un effetto quadruplo in un tempo
doppio non significa avere una «forza» quadrupla, ma semplicemente
doppia. Non è il caso di seguire nei particolari tecnici la polemica. Ci
basterà dire che essa fu risolta nel 1728 da Gian Giacomo De Mairan (1678 -1771) e meglio ancora da Giovanni d’Alembert (1717-1783) nel discorso preliminare del suo Traité de dynamique (1743). Tutta la polemica s’era fondata su un equivoco relativo alla definizione delle quantità di movimento. I cartesiani s’erano fermati alla definizione scalare data da Descartes; De Mairan mostrò che tutti gli esempi d’urto addotti nel corso della polemica obbedivano alla legge di conservazione delle quantità di moto, purché questa si considerasse, com’è, un vettore. In definitiva, nell’urto elastico si ha tanto conservazione di quantità di moto quanto conservazione di forze vive.
2.2 – UN DIBATTITO CON LEIBNIZ SULLA RELATIVITA’ DEL MOTO
Ma il dibattito con Leibniz riguardava anche altre questioni, in particolare la relatività del moto, che era diventato problema centrale da quando erano stati pubblicati i Philosophiae Naturalis Principia Mathematica (in breve: Principia) di Newton, nel 1687. In quest’opera, che ho discusso altrove, si affermavano varie cose di grandissimo rilievo che fecero discutere per moltissimi anni. Tra queste l’affermazione di spazi e tempi assoluti, con la conseguenza di una definizione precisa di moti relativi. Naturalmente sia Huygens che Leibniz intervennero su quanto era sostenuto da Newton con varie perplessità ma anche con disapprovazione. La cosa ebbe conseguenze nella corrispondenza che Huygens intratteneva con Leibniz (riporto di seguito ciò che in proposito scrive Jammer in Storia del concetto di Spazio).
Nel 1692 aveva visto la luce un’opera di Leibniz (scritta nel 1676), la Critica ai Principia Philosophiae di Descartes. Alcune cose qui sostenute, dettero origine allo scambio di opinioni tra i due scienziati. Tra l’altro, in questa Critica, si sosteneva
Se il moto non è altro che il cambiamento di un contatto o di una vicinanza immediata, ne segue che non può essere mai stabilito quale oggetto viene mosso. Infatti, come in astronomia i medesimi fenomeni sono presentati sotto differenti ipotesi, così è sempre possibile attribuire il moto reale all’uno o all’altro di quei corpi che mutano fra loro la vicinanza o la situazione; per modo che avendo arbitrariamente scelto uno di questi corpicome in quiete, o in moto, per una determinata ragione, lungo una linea data, può venire determinato geometricamente quale moto o quiete deve essere attribuito all’altro così che possa apparire il fenomeno dato. Di qui segue, che se non c’è in moto nient’altro che questo reciproco mutamento, allora non c’è in natura alcuna ragione perché il moto debba essere attribuito all’uno piuttosto che agli altri. La conseguenza di ciò sarà che non vi è alcun moto reale. Perciò, perché si possa dire che una cosa è mossa, si richiede non solo la sua situazione rispetto alle altre, ma anche che la causa del cambiamento, la forza o l’azione, sia in se stessa.
A queste righe si riferisce Huygens nella sua lettera a Leibniz del 29 maggio 1694. Egli si oppone all’asserzione “che sarebbe sconveniente che non esistessero moti reali ma soltanto relativi” (“absonum esse nullum dari motum realem sed tantum relativium”). Non importa che la citazione da Leibniz di Huygens sia inesatta. Huygens vi esprimeva la propria intenzione di attenersi alla sua teoria – forse per via del contrasto fra la propria fermezza e l’indecisione di Leibniz – e diceva che non avrebbe permesso a se stesso di restare influenzato dagli esperimenti dei Principia, convintocom’era che Newton fosse in errore. Al tempo stesso sperava che nella prossima edizione dei Principia, che pensava sarebbe stata edita da David Gregory, Newton avrebbe ritratto la sua teoria. L’istinto di Huygens nei confronti della propria teoria era giusto, sebbene sbagliasse per quanto riguarda la seconda edizione dei Principia, che di fatto fu preparata da Roger Cotes, come sbagliava quanto alla sua possibile revisione da parte di Newton.
La speranza di Huygens appare nella sua prima lettera a Leibniz, in cui si legge:
Vi dirò soltanto che nelle vostre annotazioni su Descartes, ho rilevato che voi credete che sarebbe sconveniente che non esistessero moti reali, masoltanto relativi. Cosa che, malgrado tutto, tengo per ferma, senza occuparmi dei ragionamenti e delle esperienze di Newton nei suoi Principia philosophiae, che conosco essere in errore; e desidero vedere se nella nuova edizione di questo libro, che farà David Gregory, egli si ritratterà.
La replica di Leibniz a questa lettera (22 giugno 1694) è estremamente
interessante:
Quanto alla differenza tra movimento assoluto e relativo, credo che se il
moto o piuttosto la forza motrice dei corpi è qualcosa di reale come sembra si debba ammettere, occorrerà pure che abbia un soggetto. Poiché se a e b vanno l’uno verso l’altro, ammetto che tutti i fenomeni si verificheranno nella medesima maniera, qualunque sia quello in cui si sarà posto il moto o la quiete; e quand’anche ci fossero 1000 corpi, rimango d’accordo sul fatto che i fenomeni non sapranno fornire a noi (e nemmeno agli angeli) una ragione infallibile per determinare il soggetto del moto o del suo grado; e che ciascuno potrà essere pensato a sé come in riposo, che è proprio quello che voi chiedete; ma non neghereste, credo, che ciascuno ha veramente un certo grado di moto o, se volete, di forza, nonostante l’equivalenza delle ipotesi. È vero che ne ricavo la conseguenza che nella natura v’è qualche
altra cosa che la geometria non riesce a determinare. E fra le numerose
ragioni di cui mi servo per provare che oltre all’estensione e alle sue
variazioni che sono cose puramente geometriche, bisogna riconoscere
qualcosa di superiore, ossia la forza, questa non è fra le minori. Newton
riconosce l’equivalenza delle ipotesi nel caso dei moti rettilinei; ma per i
moti circolari egli crede che lo sforzo compiuto dai corpi ruotanti per
allontanarsi dal centro o dall’asse del moto circolare riveli il loro moto
assoluto. Io, però, ho ragioni che m’inducono a credere che niente rompa la legge generale della equivalenza. Mi pare, tuttavia, che voi stesso, signore, foste già, riguardo al moto circolare, dello stesso avviso di Newton.
Come mostra questa lettera, Leibniz si trova in una situazione precaria, in quanto da un lato abbraccia il principio logico della relatività cinematica e dall’altro il fenomeno del moto circolare che richiede l’esistenza dello spazio assoluto. Il suo “moto vero” che differisce concettualmente dal puro moto geometrico, è ovviamente un tentativo di compromesso.
Ma Huygens è contrario ad ogni compromesso. Così, in una lettera datata 24 agosto 1694, scrive:
Per ciò che riguarda il moto assoluto e relativo, ammiro la Vostra memoria, in quanto vi siete ricordato che, al riguardo del moto circolare, in altri tempi ero dell’avviso del signor Newton. Il che è vero, infatti è solo da 2 o 3 anni che ho trovato una teoria più verosimile, dalla quale sembra che voi, per lo meno adesso, non siate più lontano se non per il fatto che voi volete che, quando piu corpi hanno fra di loro un movimento relativo, ciascuno di essi abbia un certo grado di moto reale, o di forza, cosa su cui non sono affatto della vostra opinione.
La replica di Leibniz del 14 settembre 1694 – replica che mise fine a questo scambio di idee estremamente interessanti, essendo morto Huygens nel 1695 – mostra il suo grande interesse per la soluzione di Huygens circa il problema del moto circolare. Egli approva che nessuno speciale privilegio venga assegnato al moto circolare rispetto al moto rettilineo uniforme e che tutti i sistemi di riferimento siano trattati come equivalenti. Secondo l’opinione di Leibniz soltanto il principio di semplicità conduce all’attribuzione di certi moti a certi corpi. Senza dubbio questo principio fu preso in prestito da Leibniz dal campo dell’astronomia, dove per molti anni giocò un .ruolo importante nella controversia tra i copernicani e i loro oppositori. Leibniz comprese non soltanto la naturale somiglianza del problema in discussione con quello della preferibilità del sistema tolemaico o di quello copernicano, ma compose anche un trattato, Tentamen de motuum coelestium causis, la cui intenzione era di mostrare come gli argomenti fondati sulla relatività meccanica del moto suggeriscano l’equivalenza dei due sistemi cosmologici antagonisti. Sembra che da principio egli intendesse pubblicare questo lavoro a Roma durante la sua visita alla Città Santa. Ma prevalse la cautela ed egli stesso sottomise al giudizio solo un Promemoria, la cui parte teorica inizia con la proposizione:
Per comprendere più esattamente l’argomento, si deve sapere che il moto è assunto in modo tale da comportare qualcosa di relativo e che non esistono fenomeni dei quali si possano determinare in assoluto il moto e la quiete; il moto infatti consiste nel mutamento di sito o luogo.
Abbiamo menzionato l’ultima lettera di Leibniz a H,uygens. Ecco la parte
che ha a che fare col problema dello spazio assoluto:
… Quando un giorno a Parigi vi dissi che era difficile conoscere il vero
soggetto del movimento e voi mi rispondeste che ciò era possibile per mezzo del moto circolare, ciò mi fermò; e me ne ricordai leggendo più o meno la stessa cosa nel libro del signor Newton; ma ciò avvenne quando già io credevo di vedere che il moto circolare non ha in questo alcun privilegio. E vedo che voi siete del medesimo avviso. Personalmente ritengo che tutte le ipotesi sono equivalenti e quando assegno certi moti a corpi determinati, io non ho né posso avere altra ragione che la semplicità dell’ipotesi, ritenendo che si possa considerare la più semplice (dopo aver tutto considerato) come l’ipotesi reale. Così, non essendoci alcun altro segno di differenziazione, credo che la divergenza fra di noi consista nel modo di parlare, che io, per
quanto posso, mi sforzo di adattare all’uso comune, salva veritate. Non
sono, però, molto lontano dal vostro modo di parlare e in un piccolo scritto che inviai al signor Viviani, e che mi sembrò adatto a convincere i Signori di Roma a permettere la teoria di Copernico, io me ne servii. Tuttavia se sulla realtà del moto nutrite queste opinioni, immagino che sulla natura deicorpi dobbiate averne di diverse da quelle che comunemente si hanno. Io ne ho di molto singolari e che mi paiono dimostrate.
Qual è questa singolare concezione della natura dei corpi sulla base della quale Leibniz può affermare di aver trovato la soluzione del problema del moto circolare ? Non lo sappiamo. Leibniz, per quanto ci è noto, non spiegala propria soluzione né qui né altrove. Quanto alla soluzione di Huygens del medesimo problema, siamo in una posizione più felice. Come può Huygens, alla luce di certi efffetti dinamici come il sorgere delle forze centrifughe nel moto circolare, mantenere il principio cinematico della relatività del moto, e al tempo stesso fare a meno dell’esistenza dello spazio e del moto assoluti ?
Nel 1886 L. Lange attirò l’attenzione sulla possibilità di trovare la soluzione di Huygens fra i suoi scritti postumi negli archivi di Leida. Fu, però, solo nel1920 che D. J. Korteweg e J. A. Schouten, avendo trovato negli archivi di Leida quattro fogli sciolti scritti da Huygens, e tutti concernenti il moto circolare, pubblicarono la soluzione. Citiamo in parte il quarto foglio, in cui Huygens riassume la soluzione:
A lungo ritenni che, a causa della forza centrifuga, il criterio del vero moto risiedesse nel moto circolare. In verità, è identico, rispetto agli altri
fenomeni, che un disco circolare o una ruota ruotino intorno a me o che
intorno al disco fermo ruoti io. Ma se una pietra viene messa sulla
circonferenza sarà proiettata solo se il disco ruota e perciò ritenni si
potesse giudicare del suo moto di rotazione senza relazione ad altro. Ma
questo effetto mostra solo che le parti della ruota, a causa della pressione esercitata sulla circonferenza, sono spinte con moto relativo fra di loro in direzioni differenti. Il moto rotatorio è quindi solo un movimento relativo delle parti, che vanno verso lati diversi, ma che sono tenute insieme da un vincolo o da una connessione. Ora, è possibile che due corpi si muovano di moto relativo fra loro senza che cambi la loro distanza ? In verità, ciò è possibile solo se si impedisce un incremento della loro distanza. Nella circonferenza esiste un moto relativo opposto. Parecchia gente ritiene che il vero moto di un corpo consiste nel suo essere trasferito da un certo posto fisso nell’universo. Ciò è sbagliato: infatti, se lo spazio è illimitato in ogni direzione, quale può essere la definizione o l’immobilità di un luogo? Si dirà forse che nel sistema di Copernico le stelle fisse sono realmente in quiete. E siano pure mutuamente immobili l’una rispetto all’altra; ma prese insieme,
relativamente a quale altro corpo saranno dette in quiete o per che cosa si distingueranno dai corpi che si muovono molto velocemente in qualche direzione? È quindi impossibile stabilire se nello spazio infinito un corpo è in quiete o in moto; perciò quiete e movimento sono soltanto relativi.
In tal modo Huygens pensa di aver scoperto che gli effetti dinamici dovuti alla presenza di forze centrifughe siano una mera indicazione del moto relativo delle differenti parti del disco. Inoltre il moto relativo di queste parti può essere trasformato a distanza assumendo come sistema di riferimento proprio quel sistema che ha la medesima velocità angolare (e la medesima origine) del disco ruotante. In questo sistema di coordinate in rotazione le parti del disco sono in quiete. Tuttavia, l’effetto dinamico riferito a questo sistema, non svanisce: la “pressione” esercitata dalle forze centrifughe non è stata, a distanza, trasformata, come avverrebbe se la forza centrifuga fosse nient’altro che un effetto dinamico del moto relativo delle particelle. La spiegazione di Huygens, quindi, non supera certamente la prova della moderna critica scientifica. Nondimeno, è un fatto storico che Huygens, ispirato dalla sua corretta conoscenza scientifica, fu il primo fisico che credette, duecento anni prima della moderna relatività, nella validità esclusiva di un principio cinematico in quanto relatività dinamica.
2.3 – IL CENTRO DI OSCILLAZIONE DI UN PENDOLO COMPOSTO
Vediamo ora, sempre con Mach, il più importante dei risultati conseguiti da Huygens nello studio dei pendoli, la determinazione del centro di oscillazione di un pendolo reale (pendolo composto) e non più ideale come quello di Galileo. Come già detto queste cose furono elaborate da Huygens nel 1661 in suoi appunti (Lavori diversi di statica e dinamica) pubblicati poi nelle Oeuvres completes e riprese in modo più completo ed articolato nella Parte IV dell’Horologium Oscillatorium del 1673(8).
Fino a quando in dinamica si considera un corpo solo, i principi di Galileo sono sufficienti, ma la trattazione del moto di più corpi agenti gli uni sugli altri costituisce un problema risolvibile solo con l’aiuto di un nuovo principio. Questo nuovo principio fu appunto trovato da Huygens.
Sappiamo che i pendoli più lunghi oscillano più lentamente di quelli corti. Immaginiamo ora che attorno a un asse ruoti un corpo pesante il cui centro di gravità cada fuori dell’asse: un tale corpo forma un pendolo composto. Ogni particella materiale di questo corpo, se fosse situata da sola alla stessa distanza dall’asse, avrebbe una sua propria durata di oscillazione. Essendo le parti del corpo vincolate tra loro, questo si muove come un tutto e la durata della sua oscillazione ha un unico valore ben definito. Immaginiamo molti pendoli di lunghezza diversa; i più corti oscillano più velocemente, i più lunghi meno. Se li
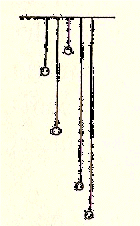
uniamo in modo da formare un solo pendolo, avverrà che il movimento dei pendoli più lunghi sarà accelerato, quello dei più corti sarà ritardato; ne risulterà una durata media di oscillazione. Avremo così un pendolo semplice di lunghezza intermedia fra la lunghezza dei più lunghi e quella dei più corti, l’oscillazione del quale avrà la stessa durata di quella del pendolo composto. Se confrontiamo la lunghezza di questo pendolo semplice con quella del pendolo composto, troviamo un punto che, malgrado il legame con gli altri punti, oscilla come se fosse solo. Questo punto è il centro di oscillazione. Mersenne propose il problema della determinazione di questo punto. Descartes ne diede una soluzione che però era insufficiente.
Huygens per primo ha trovato una soluzione generale. Oltre a lui, quasi tutti i maggiori scienziati del suo tempo si sono occupati di questo problema, e si può dire che i principi fondamentali della meccanica moderna sono tutti legati in qualche modo con esso.
Huygens partì da un’idea nuova molto importante. In tutti i casi, quali che siano le variazioni reciprocamente apportate dalle masse del pendolo ai rispettivi moti, le velocità acquistate nel moto di discesa del pendolo possono essere soltanto tali che il centro di gravità delle masse (particelle) possa risalire esattamente alla stessa altezza da cui è disceso [Principio di Torricelli, vedi Nota 4; ndr]; questo vale sia che le masse restino vincolate tra loro, sia che i vincoli siano tolti. Di fronte ai dubbi, espressi da suoi contemporanei, sull’esattezza di questo principio, Huygens fece notare che esso contiene solo l’affermazione che i corpi pesanti non si muovono da sé verso l’alto. Supponiamo che il centro di gravità delle particelle materiali vincolate tra loro nella caduta possa, per la soppressione dei vincoli, salire a un’altezza maggiore di quella da cui queste particelle sono cadute; allora ne seguirà che corpi pesanti in virtù del loro stesso peso possono salire a qualsiasi altezza, purché l’operazione venga ripetuta un numero sufficiente di volte. Se invece, dopo la soppressione dei vincoli, il centro di gravità può innalzarsi solo a un’altezza minore di quella da cui è sceso, basterebbe rovesciare il verso delle operazioni perché il corpo di nuovo si innalzi, per il suo peso, a un’altezza qualunque. La legge di Huygens enuncia un fatto di cui nessuno ha mai dubitato, e che anzi tutti conoscono istintivamente. Egli però ha usato concettualmente questa conoscenza istintiva. Non mancò di far notare l’inutilità delle ricerche intese a ottenere un moto perpetuo. Possiamo dunque riconoscere nella legge ora esposta la generalizzazione di un pensiero galileiano.
Vediamo ora quale ruolo ha questa legge nella determinazione del centro d’oscillazione. Consideriamo per semplicità un pendolo lineare OA = r, formato da un grande numero di masse indicate nella figura con punti [il pendolo OA è cioè formato da tanti pendoli di diversa lunghezza legati tra loro; ndr]. Se lo si lascia libero nella posizione OA, esso discenderà fino a H e salirà fino ad A’ dove AH = HA’. Il suo centro di gravità S salirà da una parte tanto quanto è sceso dall’altra.
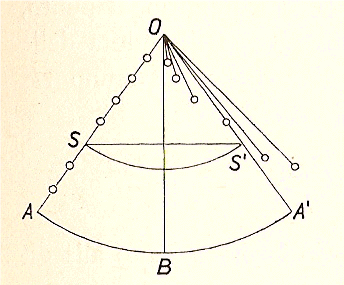
La soluzione non può ancora essere trattata da questa osservazione. Se liberiamo improvvisamente, nel momento in cui il pendolo si trova in OB, le singole masse dal loro vincolo reciproco, esse, con le velocità acquisite a causa del vincolo stesso, innalzeranno alla stessa altezza il loro centro di gravità. Se fissiamo le masse, liberamente oscillanti, alla loro altezza massima, i pendoli più corti restano al di qua della linea OA’, i più lunghi al di là di essa, ma il centro di gravità del sistema si trova in OA’, nella posizione precedente.
Osserviamo ora che le velocità impresse sono proporzionali alle loro distanze dall’asse, e che quindi, data una di queste velocità, tutte le altre sono determinate, ed è determinata anche l’altezza cui perverrà il centro di gravità. Inversamente la velocità di qualsiasi massa è determinata quando sia conosciuta l’altezza del centro di gravità. Se conosciamo in un pendolo la velocità corrispondente a una distanza di caduta, conosciamo con ciò tutto il suo movimento.
Fatte queste osservazioni, affrontiamo ora la soluzione del problema(5).
Se si considerano dei pendoli semplici di diversa lunghezza ed oscillanti con uguale ampiezza, la loro velocità al punto più basso è proporzionale alla radice quadrata della lunghezza. Riferendoci alla figura, ricordiamo che per un pendolo semplice si ha:
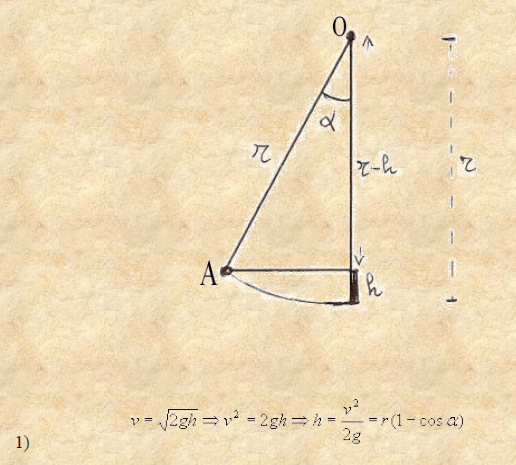
Se ora leghiamo questo pendolo ad altri di diversa lunghezza al fine di formare un unico pendolo (composto) avremo per tutti una oscillazione unica con medesima velocità. Consideriamo ora uno di questi pendoli (potrebbe essere ad esempio quello che coincide con il baricentro) ed indichiamo con rb e vb rispettivamente la sua lunghezza e velocità. Si avrà, evidentemente, che la lunghezza r e velocità v di un pendolo qualunque (tra quelli legati) e la lunghezza rb e velocità vb del pendolo considerato stanno tra loro secondo la seguente proporzione:
2) v/vb = r/rb ![]()
che vuol dire che la velocità di uno qualunque dei pendoli legati dipende dalla sua distanza r dal punto di sospensione O. E vuol ancora dire che se si confrontano pendoli liberi con i loro corrispettivi legati la velocità vL di questi ultimi sarà accelerata per i più lunghi e ritardata per i più corti(6).
Quindi, sul pendolo composto, vi sarà lungo OA un pendolo di lunghezza rb che, malgrado il legame con gli altri, oscilla come se fosse libero. E la lunghezza rb di tale pendolo rappresenta, come detto, la distanza dal punto di sospensione O al centro di oscillazione. Si tratta di calcolarsi il valore di rb e lo faccio con l’aiuto di Salvo D’Agostino.
Riferiamoci al pendolo composto di figura formato da due masse uguali m1 ed m2. Chiamiamo OB = r1 ed OA = r2 . La posizione del baricentro del pendolo, situata tra B ed A, la possiamo indicare, come già fatto, con rb. Chiamiamo poi h1 ed h2 le altezze di caduta delle masse m1 ed m2 e con hb l’altezza di caduta del baricentro.
Avremo (vedi la relazione 1):
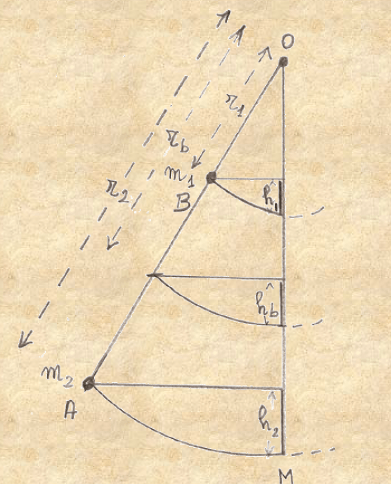

Esprimiamo ora l’altezza a cui arriverebbe il baricentro delle masse m1 ed m2 se, giunte nella posizione più bassa (corrispondente ad OM), si liberassero. Si tratta in pratica di trovare il centro di oscillazione di tale pendolo cioè quale dovrebbe essere la lunghezza r* di un pendolo semplice (con caduta h* e velocità di caduta v*) per avere lo stesso periodo di oscillazione del pendolo composto considerato (nel nostro caso formato dalle due masse m1 ed m2). Utilizzando i dati fino ad ora forniti, per la lunghezza del pendolo semplice equivalente, si trova(7):

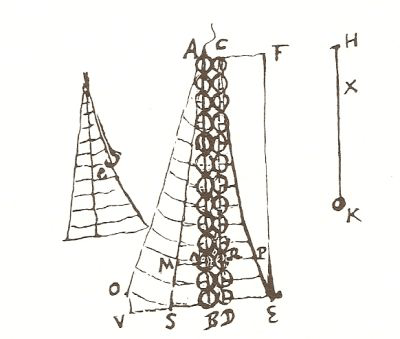
palle AB rappresenta una sbarra solida che oscilla dalla posizione AG.
Immaginò che la sbarra si divida nelle due parti componenti quando è in
posizione verticale, e la linea delle palle CD rappresenta le parti separate.
Quindi immaginò che ogni parte venga deviata SI da salire diritta. La linea
retta AS mostra 1’altezza da cui scende ogni parte della sbarra. La linea
curva CE mostra le altezze cui possono salire le parti quando si separano le
une dalle altre. Poiché il centro di gravità delle parti dopo la separazione
non può essere più alto del centro di gravità della sbarra alla sua altezza
originale, l’area triangolare ABS deve essere uguale all’area curvilinea
CDE.
2.4 – LA FORZA CENTRIFUGA
Abbiamo visto nella Parte I di questo lavoro che Huygens aveva scritto un trattato sulla forza centrifuga, De Vi Centrifuga(9), pubblicato postumo nel 1703 negli Opuscola Postuma ed aveva anche discusso di forza centrifuga nella Parte V ed ultima dell’Horologium oscillatorium del 1673 ma solo presentando alcuni teoremi senza dimostrazione. Un commento sul titolo è indispensabile: si introduce la parola forza e quindi programmaticamente Huygens si pone sulla strada complessa della dinamica, strada che aveva rifiutato quando si era occupato di urti. Probabilmente, con Westfall, l’idea era di pensare questa forza come un peso statico e quindi del tutto accettabile nella statica. L’interesse per questo problema gli nasceva dallo studio degli orologi a pendolo e dalle oscillazioni ad arco di cerchio delle masse rigide pendolari. Egli osservò che un corpo rigido che si muove di moto circolare uniforme ha la tendenza (il conatus) a spostarsi verso la periferia e, tale tendenza, è del tutto simile a quella di un corpo in caduta, e quindi dei corpi pesanti sospesi ad un filo. Per Huygens forza centrifuga e peso, erano più che fenomeni simili; essi dovevano anche essere complementari. Occorre solo aggiungere che si risente l’influsso di Descartes, non certo per le conclusioni ma per l’essersi impegnato nell’esprimere in modo quantitativo il tentativo (conatus) dei corpi di allontanarsi dal centro di rotazione. Cercherò ora di discutere i risultati che egli ricavò su una grandezza, la forza centrifuga, che fu introdotta proprio da lui.
Per trattare l’argomento, come diremmo oggi, Huygens si pone nel sistema di riferimento in moto rotatorio. Occorre aggiungere che oggi la forza centrifuga è considerata una forza fittizia poiché scegliamo sempre di studiare i fenomeni totatori da un riferimento inerziale (o fermo o in moto rettilineo uniforme). Osservando da tale riferimento noi possiamo solo dire che un oggetto in moto circolare ha la tendenza ad andare verso il centro del moto, essendo soggetto così ad una accelerazione centripeta (variazione della velocità non in modulo ma in direzione e verso)(10). Egli ipotizza una grossa ruota in rotazione su un piano orizzontale ed imperniata su un asse verticale. Prima di passare a discutere le elaborazioni di Huygens, leggiamo alcuni passi del De vi centrifuga, riferendoci alla figura seguente (sovrapposizione di due figure, la 4 e la 6, del De vi centrifuga).
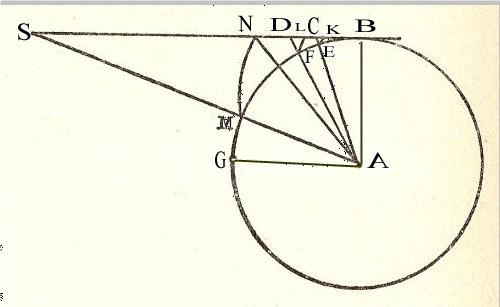
Sia una ruota BG orizzontale ruotante attorno al suo centro A. Una sfera attaccata alla sua circonferenza, quando giunge al punto B, ha una tendenza (conatus) a continuare il suo percorso secondo la retta BS tangente alla ruota nel punto B: in effetti, se essa è staccata dalla ruota e se sfugge, resterà sul percorso BS e non ne uscirà, a meno che la forza di gravità non la tragga verso il basso o che l’incontro con un altro corpo non impedisca il suo movimento. In verità, è difficile comprendere, a prima vista, perché il filo AB sia teso come è quando il globo ha una tendenza a procedere secondo BS, perpendicolare ad AB. Ma tutto diventerà chiaro con il seguente ragionamento.
Immaginiamo, inoltre, che quest’uomo tenga in mano un filo che porti attaccato alla sua seconda estremità una palla di piombo. Il filo sarà dunque teso allo stesso modo e con la stessa energia (aeque valide) per mezzo della forza di rotazione, sia che venga tenuto in questo modo, sia che vada sino al centro A e che vi sia attaccato; la ragione per la quale è teso può essere intuita molto chiaramente. Prendiamo degli archi uguali BE, EF, molto piccoli in rapporto alla circonferenza intera … L’uomo fissato alla ruota percorre questi archi in tempi eguali, e negli stessi intervalli di tempo, il piombo percorrerebbe, se venisse lasciato, dei percorsi rettilinei BK, KL uguali a questi archi, e le cui estremità K, L, non cadono in verità esattamente sui raggi AE, AF, ma, sono ad una piccolissima distanza da queste linee dalla parte di B … (Poiché queste estremità si allontanano un poco dai raggi del lato di B), accade che il globo non tenda ad allontanarsi dall’uomo seguendo un raggio, bensì una curva che tocca questo raggio nel punto in cui si trova l’uomo. ( … )
Di conseguenza, poiché il globo trascinato dalla ruota, tende a descrivere, in rapporto al raggio nel quale si trova, una curva tangente a questo raggio, si vede che il filo sarà teso da questa tendenza (conatus) esattamente come se il globo tendesse a seguire il raggio stesso.
Ma gli spazi che percorrerebbe il globo sulla suddetta curva in tempi crescenti per gradi uguali sono come la sequenza dei quadrati 1,4,9.,16, … di numeri interi, se si considera l’inizio del movimento e degli spazi molto piccoli. La figura mostra ciò nel caso in cui si
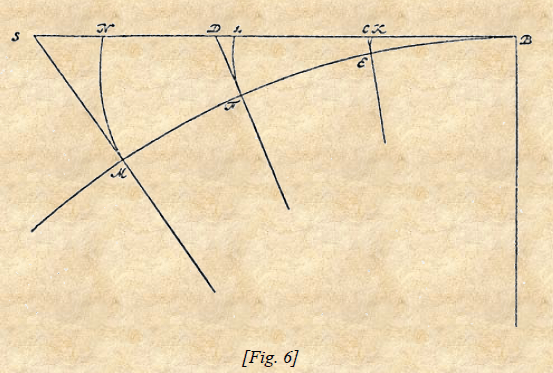
siano presi, sulla circonferenza della ruota, degli archi uguali BE, EF, FM, e sulla tangente BS dei segmenti BK, KL, LN, uguali a detti archi; poiché essendo d’altra parte i raggi EC, FD, MS. Se il globo fosse staccato nel punto B dalla ruota che gira, quando B giungesse nel punto E, il globo sarebbe nel punto K e avrebbe percorso l’elemento EK della curva qui sopra descritta; in capo ad un secondo intervallo di tempo uguale al primo, quando B fosse arrivato al punto F, il globo si troverebbe nel punto L e avrebbe percorso la parte di curva FL. .. Ma queste porzioni di curva devono essere considerate all’inizio della separazione del globo e della ruota come uguali alle rette EC, FD, MS che esse toccano, poiché si possono prendere, a partire da B, degli archi sufficientemente piccoli perché la differenza tra queste rette e gli archi stia, con la loro lunghezza in un rapporto interiore ad ogni rapporto immaginabile.
Dunque gli spazi EK, FL, MN, devono essere considerati come crescenti secondo la serie dei quadrati 1,4,9,16. E, conseguentemente, il conatus del globo trattenuto sulla ruota in movimento, sarà lo stesso che se il globo tendesse ad avanzare seguendo il raggio con un movimento accelerato nel corso del quale percorrerebbe in tempi uguali degli spazi crescenti come i numeri dispari… Da ciò trarremo la conclusione che le forze centrifughe di mobili disuguali trasportati in cerchi uguali a velocità uguali stanno tra di loro come le gravità dei mobili, cioè come le quantità solide … Ci rimane da trovare la grandezza o la quantità dei diversi conatus per le diverse velocità della ruota [Tratto da Canguilhem].
Da questa presentazione del fenomeno occorre passare alla sua formalizzazione. Intanto alcune osservazioni. La prima è relativa alla gravità che, come si può facilmente apprezzare, è considerata una tendenza verso la caduta (il conatus). La seconda riguarda come viene presentato il problema della misura della gravità: si deve misurare la velocità dell’oggetto immediatamente dopo la rottura del vincolo. E da ciò prende le mosse Huygens per discutere quantitativamente la forza centrifuga (seguirò D’Agostino).
L’uomo che si trova sulla ruota nel punto B rompe il vincolo (la corda) che teneva il corpo legato al centro A. Se questo corpo continua a muoversi con la medesima velocità, allora arriverà successivamente in K, L, … Per piccoli intervalli di tempo, tali che il conatus non faccia in tempo a distruggersi, si
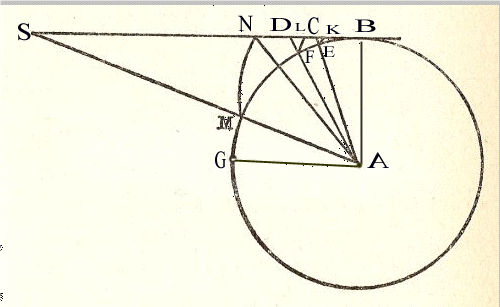
possono fare le seguenti approssimazioni: EK = EC; FL = FD. Osserviamo ora che EC ed FD aumentano con i quadrati dei tempi e ciò vuol dire che il conatus si comporta come un grave sospeso ad un filo per il quale già sappiamo che vi è una dipendenza dal quadrato del tempo. Da qui si può trarre una prima conclusione: le forze centrifughe dei corpi mobili ineguali, ma mossi secondo circonferenze eguali e con eguali velocità stanno tra loro come la gravitas o quantità solide dei corpi(11), la stessa cosa deve accadere per i corpi in rotazione, inoltre la forza centrifuga aumenta in proporzione con il peso (o materia solida) del corpo.
Prendiamo ora in considerazione il triangolo rettangolo BAD. Da esso si ricava:
AB2 + BD2 = AD2
osservando che AD = AF + FD e che AF = AB, si ha:
AF2 + BD2 = (AF + FD)2
sviluppando e semplificando:
BD2 = FD2 + 2.AF.FD
Se FD è, come nelle ipotesi, piccolo, allora FD2 è trascurabile:
BD2 = 2.AF.FD =>

Si devono ora fare delle osservazioni relativamente alla fisica del problema. La lunghezza BD è quella percorsa dall’oggetto che si allontana di moto uniforme, si avrà pertanto:
BD = vt
La lunghezza AF è il raggio r della ruota, la lunghezza FD è la lunghezza che il corpo percorre soggetto alla gravitas e quindi percorsa di moto uniformemente accelerato:

che è l’espressione nota per l’accelerazione centrifuga. Quando sarà affermata la definizione newtoniana di forza (F = ma), basterà sostituire ad a questa espressione per avere la relazione che fornisce la forza centrifuga(12). Occorre osservare che la 2) non fu data esplicitamente da Huygens ma che era completamente implicita nelle sue proposizioni.
Questo brillante studio di Huygens era finalizzato a realizzare pendoli sempre più perfezionati ed in particolare i pendoli conici, quelli costretti ad oscillare non su di un piano ma nello spazio. In un tale pendolo acquista importanza la forza centrifuga perché assume un valore che supera il peso del bilanciere e perché tale forza mantiene il pendolo non lungo la naturale linea verticale. Dice Westfall:
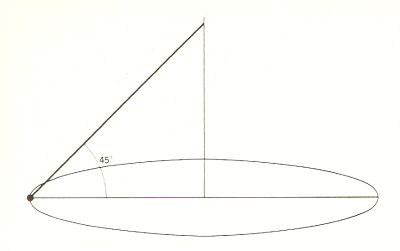
Quando la corda faceva un angolo di 45° con la verticale, intuitivamente sembrava che la forza centrifuga dovesse essere uguale al peso del bilanciere. In questo pendolo conico, il raggio della circonferenza descritta dal bilanciere era uguale all’ altezza verticale del cono, e di conseguenza (in base alla sua analisi del moto circolare) la velocità del bilanciere era uguale a quella che acquisterebbe un corpo cadendo lungo metà dell’ altezza del cono. Mediante quest’equazione, poté anche paragonare il tempo di caduta di un corpo lungo 1’altezza del cono al periodo del pendolo conico. Aveva dimostrato che tutti i pendoli conici con la medesima altezza verticale hanno lo stesso periodo e che tra pendoli che hanno diverse altezze verticali il periodo varia secondo la radice quadrata dell’altezza verticale (AB). Galileo
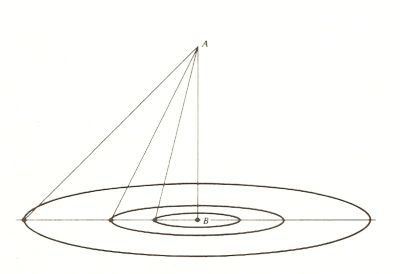
aveva mostrato che il periodo di un pendolo normale varia secondo la radice quadrata della sua lunghezza e Huygens comprese che nel caso singolo di un’oscillazione minima il pendolo conico diventa uguale al pendolo normale. Il periodo di un pendolo conico quindi è uguale al periodo di un pendolo normale la cui lunghezza sia uguale all’ altezza verticale del cono (AB). Poi, con una serie di semplici rapporti, utilizzando la propria analisi sul pendolo conico e la cinematica della caduta di Galileo, stabili che il rapporto tra il periodo di un pendolo ed il tempo di caduta lungo la sua lunghezza è uguale a p√2. Ma il periodo di caduta è √2l/g. Di conseguenza il periodo di un pendolo è 2p√l/g. Per Huygens, l’incognita dell’equazione era l’accelerazione di gravità, g. Riuscì a misurare il periodo e la lunghezza. A partire dal tempo di Galileo, moltissimi studiosi avevano cercato di misurare g misurando la distanza che un grave cadendo copre in un secondo. La maggior parte dei risultati dava g = circa 24 piedi/sec2; il gesuita Riccioli aveva trovato un dato di 30 piedi/sec2. Con il pendolo, Huygens stabili che g = 32,18 piedi/sec2, alla latitudine dei Paesi Bassi, un dato che corrisponde alla migliori misurazioni odierne.
2.5 – LA CAUSA DELLA GRAVITA’
E’ d’interesse osservare che alcune note di Huygens scritte a margine del De vi centrifuga nel 1659 ed alcune proposizioni dell’Horologium oscillatorium mostrano che Huygens aveva compreso che la forza centrifuga facesse equilibrio alla forza gravitazionale che il Sole esercita sui pianeti, in modo da mantenerli sulle loro orbite (la gravità, ipotizzata da Newton, controbilancia così bene le forze centrigughe dei pianeti e produce esattamente l’effetto dei movimenti ellittici di Kepler). Huygens, da seguace di Galileo, non indugiava spesso a speculazioni che non potesse poi sottoporre ad esperienza. Sta di fatto che rifiutava (insieme a molti altri scienziati) la concezione newtoniana di azione a distanza (a me pare assurda) poiché sembrava un cedere il passo a qualità occulte (in nota 12 vi sono altre considerazioni in proposito).
Sulla questione della gravità Huygens tornò nel 1686, nei suoi Pensées privées, scrivendo:
I pianeti galleggiano nella materia. Se così non fosse cosa impedirebbe
infatti ai pianeti di fuggirsene via, e cosa li farebbe muovere ? Keplero
assegna, erroneamente, questa funzione al sole [Oeuvres completes, Vol XXI, pag. 366].
e due anni dopo appuntò:
Vortici distrutti da Newton. Vortici di movimento sferico al loro posto.
Rettificare l’idea dei vortici.
Necessità dei vortici: la terra fuggirebbe via lontano dal sole; ma assai
distanti l’uno dall’altro e non come quelli di Descartes, l’uno contiguo
all’altro [Oeuvres completes, Vol. XXI, pagg. 437-439]
e quindi scrisse:
Il famoso Newton ha spazzato via tutte le difficoltà [relative alle leggi di
Kepler] insieme ai vortici di Descartes; ha dimostrato che i pianeti sono
mantenuti nelle rispettive orbite dalla loro gravitazione verso il sole. E che gli eccentrici diventano necessariamente ellittici [Oeuvres completes, Vol. IX, pag. 190].
Finché, nel 1690, pubblicò il suo Discours de la cause de la pesanteur, che era un’elaborazione di una conferenza che tenne alla Royal Society di Londra nel 1689, nel quale espone ampiamente le sue visioni che contrastano nettamente con quelle di Newton (seguirò qui la discussione che fa Koyré).
Questo lavoro di Huygens inizia con queste parole:
La Natura agisce attraverso delle vie così segrete ed impercettibili, portando a Terra tutti i corpi che chiamiamo pesanti, che per quanta attenzione o industria s’impiega i sensi non riescono a scoprire nulla. E ciò ha obbligato molti Filosofi del secolo passato a non cercare la causa di questo effetto mirabile che dentro i corpi medesimi e di attribuirla a qualche qualità interna e inerente che li faccia tendere in basso e verso il centro della Terra dove c’è una tendenza delle parti ad unirsi al tutto. E ciò non ci fa cogliere le cause ma supporre dei Principi oscuri e non capiti. […]
Mediante autori e studiosi moderni della Filosofia, molti hanno giustamente affermato che occorrerebbe trovare qualcosa all’esterno dei corpi che causasse le loro attrazioni ed i fenomeni che, in relazione ad esse, uno osserva [Oeuvres complètes, vol. XXI, pag 445].
Ed Huygens propende per questa seconda possibilità, rifacendosi in qualche modo a Descartes con delle sostanziali modifiche alla teoria dei vortici. Egli affermava:
Credo che se l’ipotesi principale, sulla quale io mi baso, non è quella vera, vi siano poche speranze di poterla trovare, restando nei limiti della vera e sana filosofia.
e così scriveva:
Se ci limitiamo ai corpi, senza (considerare) quella qualità che è chiamata gravità, vediamo che il loro movimento è naturalmente rettilineo o circolare; il primo è proprio dei corpi che procedono senza incontrare resistenza, il secondo di quelli che vengono trattenuti intorno a qualche centro o proprio intorno a questo centro ruotano. Conosciamo abbastanza la natura del movimento rettilineo e le leggi osservate dai corpi, quando si scontrano, nel trasmettere il loro movimento. Ma per quanto si ci sforzi di analizzare soltanto questo tipo di movimento e le reazioni che è capace di determinare nelle parti della materia, non si scoprirà tuttavia la necessità del loro tendere verso un centro. Diviene quindi indispensabile volgersi alle proprietà del moto circolare per vedere se ve ne siano alcune che possano servire al nostro scopo.
So bene che Descartes ha già tentato, nella sua Fisica, di spiegare la
gravità con il movimento di una certa materia che ruota intorno alla terra;
e torna a suo grande merito l’aver avuto per primo quest’idea. Ma,
attraverso le osservazioni che svilupperò nel resto di questo Discorso,
vedremo in che cosa la sua soluzione è diversa da quella che io proporrò, e anche da che punto di vista la consideri [Oeuvres complètes, vol. XXI, pag 455]
Sono le forze centrifughe, le cui proprietà egli qui ricorda, che lo aiutano sulla strada della sua interpretazione:
Lo sforzo di allontanarsi dal centro è, dunque, un effetto costante del
movimento circolare e sebbene questo effetto possa sembrare direttamente opposto a quello della gravità, e sebbene si sia obbiettato a Copernico che, a causa della rotazione diurna della terra, le case e gli uomini verrebbero scagliati in aria, dimostrerò tuttavia che proprio quello sforzo checompiono i corpi che si muovono di moto circolare per allontanarsi dal centro è motivo del convergere di altri verso il medesimo centro [Oeuvres complètes, vol. XXI, pag 452]
Per spiegare ciò egli introduce un’esperienzacon la quale egli credeva di poter spiegare la gravitazione mediante il moto molto veloce delle parti di un mezzo. Pose in un vaso chiuso pieno d’acqua dei pezzetti di ceralacca (cera spagnola), che essendo un po’ più pesanti dell’acqua si depositano sul fondo del vaso. Se si fa ruotare il vaso, la ceralacca si dispone ai bordi esterni del vaso; se si fa cessare improvvisamente la rotazione, l’acqua continua a girare, mentre i pezzi di ceralacca, che stanno sul fondo e il cui moto è di conseguenza frenato con maggiore rapidità, sono ora spinti verso il centro del vaso. Huygens vide in questo fenomeno una copia esatta dell’effetto della gravitazione oltre a vedervi anche i vortici cartesiani che comunque dovevano essere pensati in modi diversi da quanto aveva fatto Descartes. Scrive egli dunque:
Supporrò che nello spazio sferico che comprende la terra e i corpi che la
circondano fino a grande distanza si trovi una materia fluida, formata da
piccolissime particelle, che, in diversi modi, viene agitata in tutte le
direzioni con grande velocità. Dico che il movimento di tale materia, poiché non può abbandonare questo spazio, dato che è circondato da altri corpi, deve divenire parzialmente circolare intorno al centro; non in modo tale, comunque, che le sue particelle ruotino tutte nello stesso modo, ma piuttosto in modo che la maggior parte dei suoi movimenti si compia su superfici sferiche intorno al centro di questo spazio che diviene, per casi dire, il centro della Terra [Oeuvres complètes, vol. XXI, pag 455]
ed allora le particelle che costituiscono il vortice non ruotano più, come Descartes aveva supposto, tutte in un’unica direzione e su piani paralleli, ma in tutte le direzioni e su tutti i piani pensabili passanti per il centro della Terra. Inoltre tali vortici dovevano essere pensati molto più piccoli di quelli ipotizzati da Descartes e costituiti da particelle in moto rapido in tutte le direzioni; pensò che, in uno spazio chiuso, il moto circolare di queste particelle prevalga su quello rettilineo, e si stabilisca da se stesso. Conseguenza di ciò è che:
Non è difficile spiegare come, da questo movimento, venga generata la
gravità. Poiché, se in mezzo alla materia fluida che ruota nello spazio, come abbiamo supposto, si trovano delle parti più grosse di quelle che
compongono la materia fluida, o anche corpi formati da fasci di piccole
particelle strettamente aderenti, e [se] questi corpi non seguono il rapido
movimento della suddetta materia [fluida], saranno necessariamente spinti verso il centro del movimento e li formeranno il globo terrestre, se si suppone che la terra ancora non esista. E la ragione è la medesima che, nel sopracitato esperimento, costringe la cera spagnola ad ammassarsi al centro del recipiente. È dunque probabilmente in questo [effetto] che consiste la gravità dei corpi, e si può dire che essa [cioè la gravità] è lo sforzo che la materia fluida compie per allontanarsi dal centro e per spingere al suo posto i corpi che non seguono il suo movimento. Adesso, il motivo per cui i gravi che si vedono discendere nell’aria non seguono ilmovimento sferico della materia fluida è abbastanza chiaro; infatti, poiché v’è movimento in ogni direzione, gli impulsi che un corpo riceve si succedono l’un l’altro così rapidamente che nessuno di essi viene esercitato per un periodo di tempo sufficiente a fare acquistare al corpo un movimento sensibile [Oeuvres complètes, vol. XXI, pag 456]
In definitiva, messa a punto qualche altra questione, ha in mano la sua teoria dellagravità e può quindi concludere su Newton:
Non ho dunque niente contro la «Vis Centripeta», come la definisce il
signor Newton, che ne fa la causa del gravitare dei pianeti verso il Sole e della Luna verso la Terra; al contrario, non trovo difficoltà a dichiararmi
completamente d’accordo: infatti l’esperienza c’insegna non soltanto che
esiste in natura un’attrazione o impulso di questo genere, ma anche che esso si può spiegare con le leggi del movimento, come si vede da quanto ho scritto supra a proposito della gravità. Niente impedisce infatti che la causa di questa «Vis Centripeta» verso il Sole sia simile a quella che costringe i gravi a muoversi verso la Terra. È passato ormai molto tempo da quando si immaginò che la figura sferica del Sole potesse esser prodotta dalla medesima [causa] che, secondo me, produceva quella della Terra; ma non avevo esteso l’azione della gravità a distanze così grandi come quelle che separano il Sole dai pianeti, o la Terra dalla Luna; questo perché i vortici di Descartes, che in un primo momento mi apparvero assai verosimili, e che tenevo ancora presenti, le superavano. Neppure immaginavo, a proposito del regolare diminuire della gravità, che esso fosse inversamente proporzionale al quadrato delle distanze dai centri: una nuova ed importante qualità della gravità di cui mette conto di indagare la causa. Ma vedendo adesso, con la dimostrazione del signor Newton, che, se si suppone una simile gravità verso il Sole e che diminuisce secondo detta proporzione, essa controbilancia così bene le forze centrifughe dei pianeti e produce esattamente l’effetto dei movimenti ellittici supposti e dimostrati con osservazioni di Keplero, non posso dubitare né della verità di queste ipotesi riguardanti la gravità, né del sistema di Newton in quanto vi si fonda […]
Sarebbe diverso, naturalmente, se la supposizione fosse che la gravità è una qualità inerente alla materia corporea. Ma non credo che il signor Newton lo avrebbe ammesso perché una simile ipotesi ci allontanerebbe di molto dai principi matematici e meccanici [Oeuvres complètes, vol. XXI, pag 472-474] .
In definitiva, messa a punto qualche altra questione, ha in mano la sua teoria della gravità e può quindi concludere su Newton:
Altro punto di disaccordo con Newton ed in accordo con la sua teoria dei vortici, era la supposizione di uno spazio vuoto (e non perché avesse obiezioni contro il vuoto ma perché, come vedremo nel paragrafo che segue, era convinto che la luce si propagasse per onde e ciò non andava d’accordo, nella sua concezione, con spazi vuoti. E’ così che su questo tema conclude:
V’è solo questa difficoltà, che Newton, respingendo i vortici di Descartes,
afferma che gli spazi celesti contengono soltanto una materia molto
rarefatta, tale da consentire ai pianeti e alle comete di procedere nella loro rapida corsa incontrando un minimo di resistenza. Ma se si ammette questa estrema rarefazione degli spazi celesti, pare non sia possibile spiegare l’azione della gravità o quella della luce, almeno con i mezzi di cui mi sono servito. Per esaminare questo problema, dico che la materia eterea può considerarsi rarefatta in due modi: a) le sue particelle restano separate l’una dall’altra da un vasto spazio; b) sono l’una contigua all’altra, in modo però che la trama che ne risulta non sia eccessivamente compatta, ma piuttosto cosparsa di un grande numero di piccoli spazi vuoti. Quanto al vuoto, lo ammetto senza difficoltà e credo che sia indispensabile per il movimento dei piccoli corpuscoli tra di loro, poiché non sostengo affatto con Descartes che solo l’estensione costituisce l’essenza del corpo; aggiungo bensì ad essa la perfetta durezza che lo rende impenetrabile e impedisce che venga rotto o scalfito. Comunque, se si considera la rarefazione nel primo modo non vedo come si possa arrivare a una spiegazione della gravità; e, quanto alla luce, mi sembra del tutto impossibile, ove si ammettano tali vuoti, spiegarne la prodigiosa velocità che, secondo la dimostrazione del signor Roemer, da me riportata nel Traité de lumière, deve essere seicento volte maggiore di quella del suono. Questo è il motivo per cui ritenni che una tale rarefazione non poteva darsi negli spazi celesti [Oeuvres complètes, vol. XXI, pag 473].
2.6 – IL TRAITÉ DE LA LUMIÈRE
Nel 1691 vide la luce il Traitè de la lumière di Huygens(5). Ma l’opera era già stata fatta conoscere al momento della sua definitiva redazione, nel 1678. Nella Prefazione Huygens spiega il motivo dei 12 anni di ritardo nella pubblicazione: il breve trattato lo aveva scritto in un cattivo francese ed egli lo avrebbe voluto in un buon latino per poi inserirlo in una opera più completa (verrà pubblicato in latino nel 1728 con il titolo Tractatus de Lumine). Ci informa poi che il lavoro è rimasto lo stesso di quando lo ha scritto salvo alcune aggiunte: l’ipotesi sulla struttura dello spato d’Islanda e la scoperta della birifrangenza del quarzo.
L’opera è ampiamente incompleta e lo stesso Huygens ce lo dice. Manca ogni discussione sui colori della luce e sugli oggetti colorati e, soprattutto, non si entra a discutere la natura della luce. Gli argomenti trattati sono: la propagazione della luce, la riflessione, la rifrazione, la rifrazione da parte dell’atmosfera, la rifrazione dello spato d’Islanda, questioni di ottica geometrica. Egli si mostra insoddisfatto di tutte le teorie sulla luce fino ad allora costruite soprattutto perché sono poco chiare su questioni come il cammino rettilineo della luce e sul fatto che raggi di supposte particelle non si disturbano incrociandosi. Per Huygens la luce è movimento, solo un movimento può eccitare la visione. E poiché l’incontro tra due raggi di luce non origina disturbi, non è pensabile che la luce sia costituita da particelle. Piuttosto deve trattarsi di vibrazioni, allo stesso modo del suono. Quindi vibrazioni nel mezzo che sta in mezzo tra sorgente e ricevente e, ancora come nel suono, senza trasporto del mezzo interposto. E’ allora ad onde longitudinali, quelle caratteristiche del suono (la vibrazione si ha nella direzione di propagazione dell’onda), che pensa Huygens. Il suono poi cammina con velocità finita nell’aria, allo stesso modo della luce, come ha mostrato Röemer. Ma in quegli anni si era scoperto anche che, mentre la luce continua a muoversi in un ambiente in cui si era fatto il vuoto, lo stesso non accade per il suono (Boyle, 1660). E’ qui che subentra l’etere, questa sostanza che deve riempire l’intero universo, compenetrare di sé ogni sostanza ed essere tanto sottile da sfuggire all’aspirazione della pompa da vuoto. Ma, contemporaneamente ed ancora in analogia con il suono che si propaga meglio in mezzi più densi, l’etere deve essere uniformemente molto elastico e quindi ad elevatissima durezza per permettere le elevate velocità della luce, e la cosa non è ulteriormente indagata anche se misteriosa. Huygens passa quindi a discutere delle sorgenti di luce (radiazione) e del modo di propagazione della medesima. Inizia con un disegno famoso che riporto:
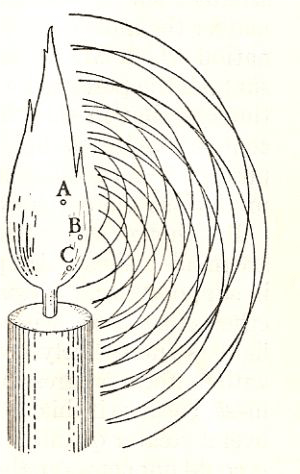
Secondo Huygens da ogni punto di una sorgente luminosa si dipartono delle onde sferiche longitudinali:
«Ogni punto di un corpo luminoso, come il Sole, una candela o un carbone ardente, emette onde il cui centro è proprio quel punto …; i cerchi concentrici descritti intorno ad ognuno di questi punti rappresentano le onde che si generano da essi … Quello che a prima vista può sembrare molto strano e addirittura incredibile è che le onde prodotte mediante movimenti e corpuscoli cosi piccoli possano estendersi a distanze tanto grandi, come, per esempio, dal Sole o dalle stelle fino a noi …».
Come è allora possibile che avvenga ciò ?
«Cessiamo però di meravigliarci se teniamo conto che ad una grande
distanza dal corpo luminoso una infinità di onde, comunque originate da
differenti punti di questo corpo, si uniscono in modo da formare
macroscopicamente una sola onda che, conseguentemente, deve avere
abbastanza forza, per farsi sentire».
Possiamo riconoscere in queste poche righe la formulazione della teoria ondulatoria fino al principio di Huygens o dell’inviluppo delle onde elementari. Lo stesso Huygens illustra questo principio con la figura seguente:
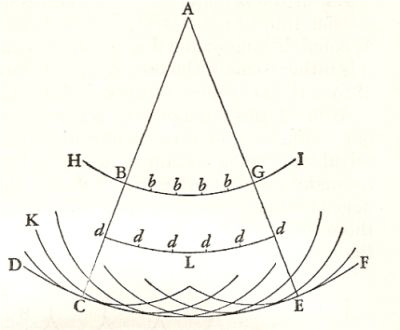
e dice:
«se DCEF è una onda emessa dal punto luminoso A, che è il suo centro, la particella B, una di quelle che si trovano all’interno della sfera delimitata da DCEF, avrà fatto la sua onda elementare KCL che toccherà l’onda DCEF in C, allo stesso momento in cui l’onda principale, emessa da A, raggiunge DCEF; è chiaro che l’unico punto dell’onda KCL che toccherà l’onda DCEF è C che si trova sulla retta passante per AB. Allo stesso modo le altre particelle che si trovano all’interno della sfera delimitata da DCEF, come quelle indicate con b e con d, avranno fatto ciascuna una propria onda. Ognuna di queste onde potrà però essere solo infinitamente debole rispetto all’onda DCEF, alla cui composizione contribuiscono tutte le altre con la parte della loro superficie che è più distante dal centro A».
Quanto ora detto può essere riassunto da quanto già sappiamo e cioè che ogni punto in cui arriva una vibrazione diventa esso stesso centro di nuove vibrazioni (onde sferiche); l’inviluppo di un gran numero di onde elementari, originate in questo modo, origina un nuovo fronte d’onda, con centro la sorgente, molto più intensa, delle onde elementari che la compongono (principio di sovrapposizione o di Huygens). Huygens proseguiva affermando che con questo modo di intendere le cose, e con l’ammissione di minore velocità della luce nei mezzi più densi, si spiegherebbero tutti i fenomeni ottici conosciuti passando poi a dare dimostrazioni della riflessione, della rifrazione, della doppia rifrazione e della propagazione rettilinea della luce.
Huygens inizia con la riflessione offrendoci questo disegno:
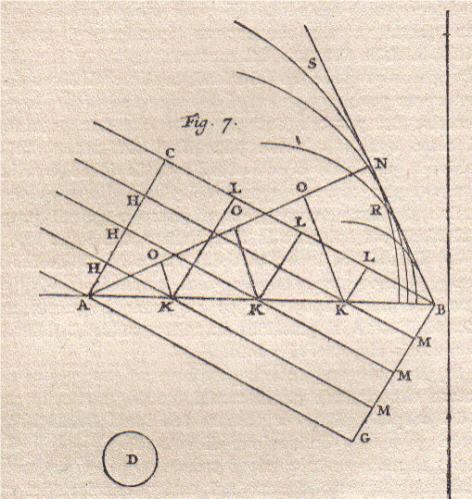
La radiazione luminosa proviene dalla sinistra ed è rappresentata dal fronte d’onda AHHHC, che è una parte di retta, in quanto la curvatura di un’onda sferica con raggio infinito è nulla. L’onda va ad incidere sulla superficie AKKKB. Il primo punto dell’onda che si riflette è A e via via lo fanno tutti gli altri (ogni punto del fronte d’onda, al momento della riflessione, diventa sorgente di una onda elementare). In figura è riportata solo la riflessione di A che, da quel punto, ritorna ad essere un’onda sferica. Ciò vale per tutti gli altri punti del fronte d’onda che, dopo essersi riflessi (ed essere tornati onde sferiche) ricostituiscono l’inviluppo che origina il fronte d’onda BN.
Il disegno per la rifrazione è invece il seguente:
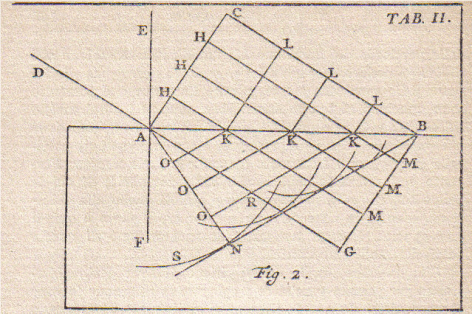
e, con ragionamento analogo a quello di prima, il fronte AHHHC, proveniente dalla sinistra, inizia a rifrangersi prima con il punto A e via via con tutti gli altri, finché non si ricostituisce il fronte d’onda BN.
Le leggi che vengono trovate sono le stesse che si avevano nel caso corpuscolare, come dimostrerò con linguaggio moderno nel paragrafo seguente. Ora basta dire che Huygens dimostra, alla fine del capitolo dedicato alla rifrazione, che il principio di Fermat (la luce impiega il tempo più breve per andare da un punto ad un altro) è in accordo con la sua rifrazione di onde.
Quando passava però a dare una spiegazione dei fenomeni che oggi si spiegano con la polarizzazione egli, molto semplicemente, affermava che non gli era stato possibile trovare nulla che lo soddisfacesse. Riguardo poi alla natura di queste onde ed al loro modo di propagazione, Huygens diceva:
«Nella propagazione di queste onde bisogna considerare ancora che ogni particella di materia da cui un’onda si diparte, deve comunicare il suo movimento non solo alla particella vicina …, ma lo trasmette anche a tutte quelle altre che la toccano e si oppongono al suo moto».
E questa è una chiara enunciazione di quella che sarà la più grande difficoltà dell’ottica ondulatoria fino a Maxwell: il fatto che le onde luminose risultavano onde di pressione e quindi longitudinali. L’ammissione, inevitabile, di onde longitudinali e non trasversali impediva di pensare a qualsiasi fenomeno di polarizzazione (e quindi questa difficoltà era alla base quanto Huygens confessava di non saper spiegare). Questo punto era ben presente a Newton che nell’Optiks lo cita e ne tenta una spiegazione ammettendo che i raggi di luce abbiano dei «lati» ciascuno dei quali dotato di particolari proprietà. Se infatti si va ad interpretare un fenomeno di polarizzazione mediante onde longitudinali, non se ne cava nulla poiché “queste onde sono uguali da tutte le parti“. E’ necessario dunque ammettere che ci sia una “differenza … nella posizione dei lati della luce rispetto ai piani di rifrazione perpendicolare.” Come già accennato solo la natura trasversale delle onde elettromagnetiche avrebbe potuto rendere conto, fino in fondo, dei fenomeni di polarizzazione.
C’è un altro aspetto che differenzia radicalmente la teoria ondulatoria da quella corpuscolare e riguarda la spiegazione del fenomeno di rifrazione (nel passaggio, ad esempio, da un mezzo meno ad uno più denso): come accennato, nella teoria ondulatoria occorre ammettere che la velocità della luce sia minore nei mezzi più densi.
Anche questo quindi diventava un elemento cruciale per decidere sulla maggiore o minore falsicabilità di una teoria. Se si fosse riusciti a determinare la velocità della luce in mezzi di diversa densità si sarebbe stati in grado di decidere quale teoria fosse più vera.
Huygens offre certamente molte novità ed lacune di estremo interesse passibili di grandi sviluppi nell’Ottocento. Ma tutta la costruzione resta deludente. Si tratta di mere deduzioni, non c’è l’accuratezza di Newton nel fare esperienze su esperienze. Non si capisce poi perché ci si fermi proprio dove la teoria ondulatoria avrebbe potuto dare il meglio di sé, nella diffrazione che non viene toccata.
2.7 – ALTRE CONCLUSIONI
Non v’è alcun dubbio che Huygens fu un vero gigante del pensiero scientifico. E, come abbiamo visto, si muove su tutte le strade aperte da Galileo, con ogni curiosità su argomenti che in quegli anni sorgevano da ogni parte. Dal punto di vista scientifico egli era un perfetto laico che mai fece riferimenti ad un qualche Dio nel descrivere il funzionamento del mondo. Passi in avanti se ne erano fatti molti rispetto a Descartes, anche se alcuni suoi contemporanei (newton e Leibniz) rimisero Dio dentro le cose del mondo.
Più in generale Huygens ebbe la ventura di fare da ponte tra Galileo e la cultura del Sud Europa con Newton ed il nuovo mondo che si faceva strada. Anche se i suoi contributi sono di una personalità eccezionale, egli non riuscì ad emergere come i suoi meriti gli avrebbero permesso. Da una parte le guerre anche di religione e la transizione dal latino alle lingue volgari locali che lo trovarono in difficoltà perché egli non era un buon conoscitore né del francese né dell’inglese. Il suo olandese non era ancora lingua diffusa ed il tedesco ancora non emergeva a livello scientifico. Così egli affastellò opere che non furono pubblicate a tempo debito ed i suoi meriti non ebbero la risonanza che sarebbe stata auspicabile.
Ancora oggi si trova poco in giro su Huygens, particolarmente nel panorama provinciale italiano. Cose sparse, suoi contributi qua e là. Mai nulla di organico (a parte il citato libro della D’Elia che però è introvabile). La tradizione esterna alla meccanica newtoniana di uno dei seguaci del metodo di Galileo fu soffocata dall’emergere possente della figura di Newton che, paradossalmente, congelò la ricerca scientifica per circa un secolo: la sua opera era considerata dai più talmente ben fatta ed esaustiva che sembrava impossibile dire qualcosa di nuovo e di più completo. Si dimostra ancora che l’indeterminatezza logica delle teorie è un possente motore per progredire.
Su Huygens dice Mach:
Per quanto riguarda la forma dell’esposizione dell’Horologium
oscillatorium, bisogna dire che Huygens divide con Galileo il merito di una completa e nobile sincerità. Egli espone infatti apertamente i metodi di cui si è servito nelle ricerche, permettendo così al lettore di arrivare a una perfetta comprensione delle sue scoperte. Né vede alcuna ragione per tenerli nascosti. Se fra mille anni il suo nome sarà ancora presente alla memoria degli uomini, verrà ricordato come quello di uno scienziato di eccezionale grandezza. Nella nostra esposizione dei lavori huygensiani dobbiamo procedere in modo diverso da quello usato per Galileo. Infatti le trattazioni di Galileo, nella loro classica semplicità, possono essere esposte senza modificazioni, mentre questo non è possibile per Huygens, che studia problemi più complicati, servendosi di notazioni e metodi matematici, per noi insufficienti e lenti.
A ciò aggiunge D’Agostino:
In complesso, attraverso la lettura dei lavori di Huygens risalta il 1avoro
sperimentale che era stato fatto col pendolo in questi anni, lo scambio di
informazioni sui risultati, osservate anche in viaggi oceanici. Un contesto
veramente assai differente di quello presente a Galileo: la nuova fisica non è più mediterranea, nello stesso senso in cui era mediterraneo il Rinascimento e l’uomo del Rinascimento.
Ed è amaramente vero. Il baricentro della ricerca che ancora nella prima metà del Seicento era localizzato in Italia, grazie alla distruttrice opera della Chiesa, si era trasferito al Nord e si sente dall’apertura del dibattito che prescinde dal doversi giustificare per ogni cosa detta e financo pensata. E’ il clima che è indispensabile alla ricerca, un clima di libero pensiero con la concessione dei soli condizionamenti che uno vuol porre a se stesso. Dalla metà del Seicento l’Italia fornirà scienziati alle varie corti europee. I nostri scienziati dovranno fare gli inventori per procurarsi il denaro che serviva loro per qualche ricerca. Mentre a Roma si faceva la Fisica Sacra. Fino al miracolo Fermi e scuola di Roma. Ma anche qui ci pensò Mussolini a fare di nuovo tabula rasa. Meno male che un certo Amaldi … Ma oggi, ormai da qualche anno, la distruzione è ancora in atto. La Chiesa trionfa e la scienza deve sempre scontare qualche suo peccato capitale.
NOTE
(1) Riporto la traduzione inglese del lavoro di Huygens, ON THE MOTION OF BODIES RESULTING FROM IMPACT. Ad essa mi riferirò nel seguito.(2) Una situazione sperimentale identica era stata immaginata in precedenza da Giordano Bruno ne La cena de le Ceneri del 1584 (circa 90 anni prima) per introdurre il problema della relatività del moto attraverso la discussa questione della deviazione dalla verticale di un corpo in caduta. L’esperienza suggerita da Bruno era la seguente:
Teo. Or, per tornare al proposito, se dunque saranno dui, de’ quali uno si
trova dentro la nave che corre, e l’altro fuori di quella, de’ quali tanto l’uno quanto l’altro abbia la mano circa il medesmo punto de l’aria, e da quel medesmo loco nel medesmo tempo ancora l’uno lasci e scorrere una pietra e l’altro un’altra, senza che gli donino spinta alcuna, quella del primo, senza perdere punto né deviar da la sua linea, verrà al prefisso loco, e quella del secondo si trovarrà tralasciata a dietro. Il che non procede da altro, eccetto che la pietra, che esce dalla mano de l’uno che è su stentato da la nave, e per consequenza si muove secondo il moto di quella, ha tal virtù impressa, quale non ha l’altra, che procede da la mano di quello che n’è di fuora; benché le pietre abbino medesma gravità, medesmo aria tramezzante, si partano (e possibil fia) dal medesmo punto, e patiscano la medesma spinta. Della qual diversità non possiamo apportar altra raggione, eccetto che le cose, che hanno fissione o simili appartinenze nella nave, si muoveno con quella; e la una pietra porta seco la virtù del motore il quale si muove con la nave, l’altra di quello che non ha detta participazione. Da questo manifestamente si vede, che non dal termine del moto onde si parte, né dal termine dove va, né dal mezzo per cui si move, prende la virtù d’andar rettamente; ma da l’efficacia de la virtù primieramente impressa, dalla quale depende la differenza tutta. E questo mi par che basti aver considerato quanto alle proposte di Nundinio.
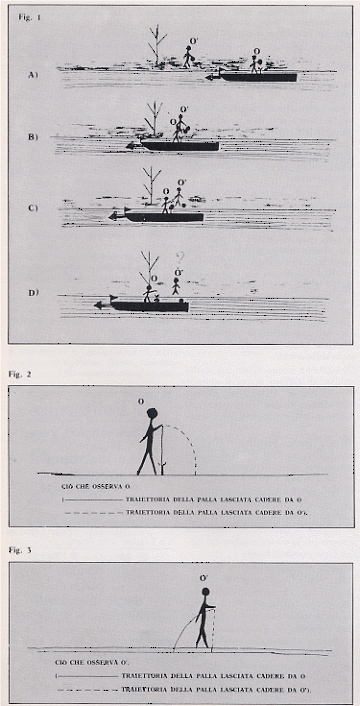
Tradotto in un linguaggio più comprensibile, ciò vuol dire quanto segue. Supponiamo che una barca, trasportata dalla corrente di un canale, marci velocemente vicinissima alla sponda. Sulla barca c’è un osservatore O e sulla riva un osservatore O’. Ambedue gli osservatori tengono le braccia tese: O verso la riva ed O’ verso la barca. Ciascun osservatore tiene in una mano una palla di ferro (figura 1a). Appena la barca porta O ed O’ a sfiorarsi le mani (figura 1b), i due osservatori lasciano cadere la palla di ferro che hanno in mano, in modo che ambedue le palle cadano sulla coperta della barca. Cosa osserva O dalla barca? La palla che egli ha lasciato è caduta perpendicolarmente sulla coperta della barca, mentre la palla lasciata da O’ ha seguito, per O, una traiettoria obliqua (figure 1e e 1d), tant’è vero che è caduta più indietro rispetto a quella lasciata da O (la palla lasciata da O era dotata della velocità orizzontale della barca, mentre la palla lasciata da O’ cadeva con velocità iniziale nulla e la barca gli sfuggiva sotto). Le figure 2 e 3 riportano, rispettivamente, le traiettorie delle palle osservate da O e da O’.
Con questa esperienza Bruno riesce, in modo eccellente, a ribaltare il problema: cambiando punto d’osservazione, è sulla Terra che si hanno deviazioni dalla caduta verticale; su una nave, invece, anche se essa è in moto, le cose vanno come se fosse ferma (principio dinamico di relatività). È importante osservare che moto della Terra, composizione dei movimenti, principio d’inerzia e relatività del moto si affermano come un’unica problematica.
(3) Huygens come Galileo non ha un concetto chiaro di massa e quindi parla di uguaglianza tra corpi. Nel seguito del testo parlerò anche io di masse. Dal contesto è chiaro che il suo è un riferimento a masse uguali. il concetto di massa sarà definito formalmente per la prima volta da Newton, non senza vari problemi di circolarità del suo discorso. Per maggiori dettagli, si veda Roberto Renzetti, Massa e Peso.
(4) A chiosa di questo lavoro di Huygens dice Westfall:
Quando due corpi duri si scontrano, se uno di essi conserva dopo l’urto tutto il moto che aveva, neanche l’altro perde né guadagna alcun moto. Ed Huygens dimostrò che ciò poteva verificarsi solamente quando le grandezze dei corpi erano inversamente proporzionali alle loro velocità. Ma affermare che ciò poteva avvenire solamente in tali condizioni significava dire anche che ciò avveniva in ogni urto, perché la relatività del moto permetteva in ciascun caso di scegliere un presupposto teorico secondo cui le loro velocità avranno tale rapporto con le loro grandezze. Rispetto al loro centro di gravità comune, le grandezze di due corpi nell’urto sono sempre inversamente proporzionali alle loro velocità, e dopo l’urto i corpi si separano alle medesime velocità con cui si sono avvicinati. Il centro di gravità naturalmente non subisce cambiamento di sorta. Esiste, concludeva Huygens, «un’ ammirevole legge di natura» che appare valida per tutti gli urti di tutti i corpi. È che il centro di gravità di due o tre o un numero a piacere di corpi si muove sempre, prima e dopo il loro urto, uniformemente in linea retta nella stessa direzione. Vale a dire, l’urto può essere risolto applicando il principio di Torricelli [“Due gravi insieme congiunti non possono muoversi da sé, se il loro comune centro di gravità non si abbassa” (Torricelli, Opere geometriche, pag. 158); ndr]. Mentre questi l’aveva applicato solamente al moto verticale nel caso di due corpi costretti a muoversi insieme, Huygens l’applicò anche ai moti inerziali di corpi non congiunti. Un sistema isolato di corpi può essere considerato come un corpo singolo che sta intorno al loro centro di gravità comune. Da questo punto di vista, era possibile una discussione puramente cinematica dell’urto, senza fare riferimento di sorta alla forza della percossa. La parola «forza» non compariva nel titolo del trattato di Huygens, De motu corporum ex percussione. Nonostante correggesse ampiamente Descartes, la sua visione
dell’urto includeva aspetti fondamentali di quella cartesiana. Nell’urto non avviene azione dinamica di sorta; dal punto di vista del centro di gravità, la direzione del moto di ciascun corpo cambia istantaneamente, ma entrambi si allontanano dall’urto mantenendo inalterati i loro moti originali.
(5) La dimostrazione di Huygens, nella sua traduzione francese, si trova in Huygens, Oeuvres completes, Vol. XVI, pagg. 420-428 e si può consultare qui. Si trova in Lavori diversi di statica e di dinamica ed è del 1661.
(6) Partendo dalla relazione 2) riportata nel testo, con semplici sostituzioni si trova:
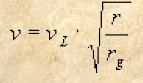
da cui si vede che: se r < rg, la radice risulterà minore di uno; se r > rg allora la radice risulterà maggiore di uno.
(7) Riporto, per il lettore che non volesse accettare il dato così com’è, i calcoli necessari che sono lunghi ma elementari. Osservo che tutto questo oggi si risolve semplicemente con il calcolo differenziale che, all’epoca, ancora non era stato sviluppato. In particolare il centro di oscillazione r* viene introdotto nei moderni trattati di fisica, mediante le equazioni cardinali della dinamica elaborate da Euler
Si parte dalla relazione 3) del testo, nella quale occorre inserire, in luogo di hb ed rb, le nostre incognite h* ed r* e sviluppare con passaggi successivi.

Fatto ciò, nell’espressione ottenuta, sostituiamo alle velocità v le espressioni che si ottengono dalla 2) del testo.
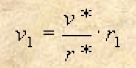

:

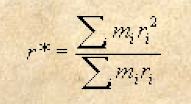
e la quantità che compare al numeratore sarà chiamata da Euler momento d’inerzia (un concetto che Mach definisce di economia nella meccanica) mentre la quantità che compare al denominatore prenderà il nome di momento statico della massa di un pendolo.
(8) Riporto la traduzione inglese della Parte IV del lavoro di Huygens, divisa in due HOROLOGIUM OSCILLATORIUM Parte IVa ed HOROLOGIUM OSCILLATORIUM Parte IVb. Il resto della traduzione inglese dell’Horologium si può trovare in http://www.17centurymaths.com/contents/huygenscontents.html.
(9) Riporto DE VI CENTRIFUGA nella sua traduzione inglese.
(10) Dice Mach in proposito:
Se si accetta il principio galileiano che la forza determina accelerazione,
necessariamente va attribuita a una forza ogni variazione di velocità, e
quindi ogni variazione nella direzione del moto (giacché la direzione è
determinata da tre componenti della velocità perpendicolari fra loro). Se
dunque un corpo sospeso a una corda, per esempio una pietra, è fatto ruotare con moto circolare uniforme, la traiettoria curvilinea è spiegabile solo supponendo che una forza costante faccia deviare il corpo dalla traiettoria rettilinea. La tensione della corda è questa forza che fa deviare dalla linea retta il corpo e lo tira verso il centro del cerchio. La tensione rappresenta dunque una forza centripeta. D’altra parte la tensione del filo agisce anche sull’asse o sul centro fisso del cerchio, e quindi si presenta come forza
centrifuga.
(11) Si osservi che l’espressione usata da Huygens, quantità solida, non può essere altro che la massa. Si osservi anche che l’influenza della sua formazione cartesiana (teoria dei vortici) faceva considerare ad Huygens il peso come una mancanza di forza centrifuga: la caduta di una pietra avviene in corrispondenza ad una piccola quantità di materia che si allontana dalla Terra.
(12) A commento della scoperta di Huygens dell’accelerazione centrifuga e delle conseguenze che ne derivavano nella spiegazione della gravità, dice Dijksterhuis:
Fra le varie applicazioni per le quali Huygens fece uso della sua teoria del moto circolare uniforme citiamo specialmente il pendolo conico, una
particella appesa a una corda priva di massa, che descrive un cono circolare retto. Questo caso presentava per lui un interesse particolare in connessione con la costruzione di orologi a pendolo. L’importanza della teoria della forza centrifuga di Huygens per la meccanica teorica consiste principalmente nel fatto che essa rendeva assolutamente chiaro che il mantenimento di un moto curvilineo, anche se è uniforme, richiede l’azione costante di una forza (la tensione esercitata lungo la corda è tale da neutralizzare la forza centrifuga).
Così una vecchia, ma mai completamente sradicata, concezione dell’inerzia, la quale riteneva che una particella, una volta che si trovasse in moto lungo un cerchio, avrebbe continuato a muoversi in questo moto circolare, qualora fossero state eliminate tutte le influenze esterne, veniva così definitivamente confutata. E’ inoltre importante il fatto che un moto curvilineo uniforme possiede un’accelerazione (giacché questo è, propriamente parlando, il risultato a cui porta la linea di pensiero di Huygens, anche se egli non usa la parola “accelerazione”) si basa sul fatto che la variazione di una velocità (il requisito per la presenza di una accelerazione) può anche consistere esclusivamente in un mutamento di direzione; e ciò equivale al riconoscimento del carattere vettoriale di una velocità.
Sullo stesso argomento dice Mach:
Con l’aiuto della sua teoria Huygens fu in grado di spiegare immediatamente tutta una serie di fenomeni. Quando, per esempio, si scoprì che un orologio a pendolo trasportato da J. Richer da Parigi a Caienna (1671-73) ritardava nel suo movimento, Huygens osservò che la forza centrifuga dovuta alla rotazione della terra è maggiore all’equatore, e ne dedusse la diminuzione dell’accelerazione gravitazionale g, dando così la spiegazione del ritardo.
Ed in proposito aggiunge Dijkstheruis:
Huygens introduceva una nuova specie di materia dotata di un particolare grado di sottigliezza ogni volta che ne avesse bisogno per la spiegazione di un fenomeno. Così c’era una materia per la spiegazione dei fenomeni magnetici, una per i fenomeni elettrici e una per render conto del fenomeno da lui scoperto – che un liquido che non contenga aria può rimanere in un tubo barometrico a un livello molto più alto di quello che corrisponde alla pressione atmosferica. Ma non sempre è chiaro se anche più tardi abbia continuato a distinguere tra due tipi siffatti di materia. E nel Traité de la lumière, per dare una spiegazione del fatto che vi sono corpi che non trasmettono affatto la luce (i metalli) si suppone persino che tra le particelle dure ve ne siano alcune molli, le quali ricevono gli impulsi di etere, ma non li trasmettono. Ma allora questa mollezza avrebbe a sua volta dovuto venir spiegata supponendo che queste particelle fossero composte da particelle ancora più piccole, le quali avrebbero dovuto a loro volta essere dure. Ciò mostra in maniera convincente come la concezione puramente meccanicistica, la quale non riconosce altre qualità all’infuori della dimensione, della forma e del movimento, coinvolgesse gli scienziati nelle massime difficoltà non appena essi cominciavano a studiare i fenomeni in maniera esaustiva. E tuttavia, accettando la durezza come una proprietà originaria, Huygens si allontanava già dalla posizione strettamente
E D’Agostino, per parte sua, conclude:
La pesantezza o peso è spiegata in questo lavoro come effetto dell’urto o pressione nelle particelle dell’etere che circonda i corpi sui corpi stessi
ed in questo senso viene modificata la teoria di Descartes del trascinamento (che, fra l’altro, non spiegava il moto retrogrado di alcune comete), Huygens si chiede anche come i corpi possono essere ancora pesanti quando si muovono con una velocità uguale a quella delle particelle urtanti di etere: ma le particelle di etere sono accelerate ed in questo fatto Huygens crede di trovare una spiegazione anche alla legge di. uguale accelerazione di caduta dei gravi scoperta da Galilei. (vedi, in questi tentativi di spiegazione per urto, oltre che un ritorno al quadro Cartesiano, anche un inizio di quei concetti che saranno ripresi dalla teoria cinetica dei gas). Si accenna arche all’esperimento eseguito dalla spedizione alla Caienna, un paese dell’America centrale, sulle oscillazioni del pendolo: il fatto che le oscillazioni in quel paese equatoriale sono più lente, cioè g è minore che a Parigi, viene spiegato con la presenza della forza centrifuga (sic) senza tener conto dello schiacciamento terrestre.
BIBLIOGRAFIA
1 – U. Forti – Storia della scienza – Dall’Oglio 1968
2 – L. Geymonat (diretta da) – Storia del pensiero filosofico e scientifico – Garzanti 1970
3 – R. Tatón (coordinata da) – Storia generale delle scienze – Casini 1964
4 – Hugh Kearney – Science and Change 1500 – 1700 – Weidenfeld and Nicolson. 1971
5 – H. Butterfield – Le origini della scienza moderna – il Mulino 1962
6 – Richard S. Westfall – La rivoluzione scientifica del XVII secolo – il Mulino 1984
7 – Paolo Rossi – La nascita della scienza moderna in Europa – Laterza 2000
8 – Maurizio Mamiani – Storia della scienza moderna – Laterza 2002
9 – Paolo Rossi (diretta da) – Storia della scienza – UTET 1988
10 – Robert Lenoble – Le origini del pensiero scientifico moderno – Laterza 1976
11 – A. Rupert Hall – Da Galileo a Newton – Feltrinelli 1973
12 – E.J. Dijksterrhuis – Il meccanicismo e l’immagine del mondo – Feltrinelli 1971
13 – Carl B. Boyer – Storia della matematica – Mondadori 1980
14 – Morris Kline – Matematical thought from ancient to modern times – Oxford University Press, 1972
15 – Maurice Daumas (a cura di) – Storia della scienza – Laterza 1976
16 – Nicola Abbagnano (coordinata da) – Storia delle scienze – UTET 1965
17 – I. Bernard Cohen – La rivoluzione della scienza – Longanesi 1988
18 – A.R. Hall e M. Boas Hall – Storia della scienza – il Mulino 1979
19 – Charles Singer – Breve storia del pensiero scientifico – Einaudi 1961
20 – Salvo D’Agostino – Dispense di Storia della Fisica (a.a. 1972/73) – IFUR 1972.
21 – Roberto Pitoni – Storia della fisica – S.T.E.N. 1913.
22 – Mary B. Hesse – Forze e campi – Feltrinelli 1974.
23 – David Park – Natura e significato della luce – McGraw-Hill 1998.
24 – Dava Sobel – Longitudine – Rizzoli 1999.
25 – L. Figuier – La ciencia y sus hombres – D. Jaime Seix Editor 1880.
26 – Friedrich Klemm – Storia della tecnica – Feltrinelli 1966
27 – C. Truesdell – Essays in the History of Mechanics – Springer-Verlag 1968
28 – Edmund Whittaker – A History of Theories of Aether and Electicity – Nelson and Sons 1954
29 – Ernst Mach – La meccanica nel suo sviluppo storico-critico – Boringhieri 1968
30 – G. Canguilhem – Introduzione alla storia delle scienze – Jaca Book 1973
31 – David Park – Natura e significato della luce – Mc Graw Hill 1998
32 – Max Jammer – Storia del concetto di forza – Feltrinelli 1971
33 – I. Bernard Cohen – La rivoluzione newtoniana – Feltrinelli 1982
34 – Alexander Koiré – Studi newtoniani – Einaudi 1972
35 – Christiaan Huygens – Treatise on light – Encyclopaedia Britannica 1952
36 – Giordano Bruno – La cena delle ceneri, in: Bruno e Campanella, Opere, Ricciardi 1956
37 – Amos Funkenstein – Teologia ed immaginazione scientifica dal Medioevo al Seicento – Einaudi 1996
38 – Max Jammer – Storia del concetto di spazio – Feltrinelli 1966.
Categorie:Galileo Galilei
Rispondi