Roberto Renzetti
UN CENNO AL SETTECENTO
L’Illuminismo, che si ispira alla filosofia di Newton e di Locke e che ha nel primo un riferimento costante come rappresentante della ragione scientifica (osservazioni sperimentali e conseguenti elaborazioni teoriche, con la matematica, delle medesime) contro ogni metafisica, si svolse essenzialmente su tre grandi linee-guida:
1) La ragione è in grado di spiegare tutti i più grandi problemi dell’uomo. Lo spirito
scientifico ha il primato su ogni forma di oscurantismo.
2) L’uomo ‘illuminato’ ha il dovere di difendere la cultura. Occorre che i filosofi naturali, essi stessi, facciano i divulgatori dello spirito scientifico. L’operazione di divulgazione porta con sé il superamento delle vecchie credenze che sono ancora alla base della diffusione, e quindi del potere,della religione.
3) La condizione umana può essere radicalmente migliorata proprio dall’abbattimento di miti, pregiudizi, superstizioni. L’uomo che si è impadronito dello spirito scientifico può progredire.
Questa grande fiducia nelle possibilità, dell’uomo nasceva certamente dai grandi successi che, nel secolo precedente, la filosofia naturale aveva conseguito. Ed il massimo sintetizzatore di quei successi e di quella filosofia naturale era proprio Newton che ora si ergeva a modello da imitare. Con l’uso dei metodi scientifici indicati da Newton e con i principi filosofici enunciati da Locke sarebbe stato possibile sbarazzarsi dei residui scolastici e metafisici presenti in Descartes ed in Leibniz. D’altra parte le filosofie cartesiana e leibniziana rispondevano bene agli interessi di chi manteneva vecchi privilegi e pertanto, da questi ultimi, erano state accettate e rese funzionali al loro sistema di potere. La lotta quindi contro il cartesianesimo ed il leibnizianesimo, per l’affermazione della filosofia di Newton, aveva in sé una grande carica rivoluzionaria e si configurava come lotta di potere con l’illusione che, di per sé, l’affermazione del newtonianesimo avrebbe comportato quella di nuove classi sociali (la borghesia).
Fu certamente il grande impegno di un uomo come Voltaire (1694-1778) che riuscì a far conoscere al grande pubblico francese l’opera di Newton. Furono poi i lavori di Condillac, Helvetius, Diderot, D’Alembert e molti altri fino a Laplace che imposero la filosofia di Newton nel continente. Ma questo passaggio dall’Inghilterra al resto d’Europa avverrà con notevoli cambiamenti della stessa. Pur mantenendo formalmente l’azione a distanza della gravitazione universale, si introdurranno modelli fluidistici (calore, elettricità, magnetismo) che di fatto hanno bisogno di una trattazione ‘a contatto’; le forze, che nonostante tutto risultano oscure e vaghe, non sono più considerate come cause di accelerazioni ma come semplici variabili delle equazioni differenziali che ne formulano le condizioni di equilibrio e di conservazione; l’etere, che per Newton assolveva un ruolo importante, viene piano piano accantonato; lo spazio ed il tempo perdono il loro ruolo centrale diventando meri elementi di calcolo; le equazioni del moto si vanno sempre più configurando come ristrutturazione e non come ampliamento delle premesse newtoniane; Dio scompare nella spiegazione e nel sostegno del mondo.
Dunque il movimento illuminista, in Francia, si staccò sempre più radicalmente dal razionalismo aprioristico di tipo cartesiano per abbracciare un nuovo tipo di razionalismo fondato su fatti empirici. In definitiva si lavora sempre più per risolvere problemi concreti piuttosto che occuparsi di concezioni del mondo. Le questioni tecniche, nel secolo precedente affidate in gran parte alla pratica del lavoro artigianale, vengono sempre più sottomesse a trattamento teorico e questo fatto comporterà un progressivo avvicinamento tra scienza e tecnica (anche se per tutto il XVIII secolo almeno, sarà la tecnica ad avere il primato delle conquiste più originali e feconde). Anche qui con i dovuti distinguo. Mentre infatti in Inghilterra, ancora per lungo tempo, il fatto tecnico potrà evolversi autonomamente e con grande e riconosciuta dignità come conseguenza della scelta, fatta dalla cultura inglese, di prendere a modello lo sperimentalismo dell’ 0ptics di Newton per avvicinarsi alla comprensione dei fenomeni, ben altrimenti le cose si svolgeranno in Francia. In questo paese il modello metodologico cui i filosofi della natura si ispirano è quello matematico dei Principia e, non a caso proprio in Francia, la Meccanica diventerà Meccanica Razionale, Meccanica cioè che partendo dal fatto concreto, nel suo svolgersi, sempre più perde di vista il punto di partenza per passare ad elaborazioni in cui la
matematica assume un ruolo determinante e che sempre di più usa di metodi propri della matematica stessa. Si lavora per fornire alla Meccanica una validità scientifica che non dipenda più dalle semplici osservazioni empiriche. Si tratta di ricavare tutti i fenomeni e tutte le leggi da alcuni principi molto generali. All’interno poi dei processi di elaborazione matematica dei lavori di Newton che, come abbiamo già accennato, trascendono l’opera stessa del nostro per configurarsi come ristrutturazione piuttosto che come generalizzazione di quest’opera, scaturiranno fatti nuovi come conseguenza della mera formalizzazione della teoria. La matematica non può qui, in alcun modo, essere considerata come puro e semplice strumento tecnico, come linguaggio che descrive fatti già noti, ma, al contrario, come qualcosa che, partendo dalla descrizione dei fenomeni, è in grado di predirne degli altri al suo interno. Sempre più quindi la matematica diventerà indispensabile per comprendere le tematiche in discussione e per poterne discutere con cognizione. Ed il filosofo che si sente sfuggire l’immediata lettura di un fatto naturale a causa del suo occultamento in equazioni via via più complesse, non potrà far altro che richiamarsi alla realtà che lui conosce, quella che i sensi gli sottopongono (ad esempio: Berkeley). La potenza della matematica, nell’interpretazione e nella predizione di nuovi fenomeni, era molto chiara agli addetti ai lavori dell’epoca e questa potenza risulta tutta nella meccanica razionale (ed analitica). La meccanica razionale, con Baracca e Livi, è una scienza che studia rigorosamente (a partire da un ristretto numero di leggi generali – n.d.r.) i sistemi meccanici perfetti, macchine ideali senza attriti, sul modello della ‘macchina celeste’, retta da forze agenti a distanza lungo la congiungente con intensità [inversamente] proporzionale al quadrato della distanza.” E quindi, in nome del meccanicismo newtoniano, Lagrange (1736-1813) potrà affermare nella prefazione della sua Meccanica Analitica (1788): “Non si troveranno figure in quest’opera. I metodi che io espongo non richiedono né costruzioni né ragionamenti geometrici o meccanici, ma solamente operazioni algebriche soggette ad un andamento regolare ed uniforme. Quelli che amano l’Analisi vedranno con piacere la meccanica divenirne una nuova branca e mi saranno grati d’averne esteso così il dominio.“
Ed anche D’Alembert, come del resto tutta la scienza che si affermò come ufficiale, non era alieno da avere una visione aristocratica del progresso sociale, in ogni caso condizionato dalla conoscenza “dei principi razionali e matematici”. Alcuni però iniziarono una revisione di questa concezione e “Diderot, in particolare, attaccò, in De l’Interpretation de la Nature (1753), l’eccessiva matematizzazione della scienza francese nel quadro di una rivalutazione baconiana della pratica degli artigiani.”
Per tutto il ‘700, comunque, la Francia privilegerà la scienza teorica pura, mentre l’Inghilterra la scienza sperimentale ed applicativa (solo nei primi anni dell’ Ottocento questo dato si invertirà ed, in particolare, in Francia ci si occuperà di problemi applicativi soprattutto al fine di sostenere le necessità degli eserciti di Napoleone). In ogni caso, quanto abbiamo detto sull’accettazione della filosofia di Newton da parte degli illuministi francesi, non deve far intendere che non permanessero fortissimi influssi cartesiani che si compenetravano via via sempre di più con alcune problematiche leibniziane. Ed a proposito degli influssi di Leibniz sul Settecento francese, si osservi, con Cassirer, che “D’Alembert, pur combattendo anche lui i principi della metafisica leibniziana, manifestava sempre la più grande ammirazione per il genio filosofico e matematico di Leibniz; e l’articolo di Diderot su Leibniz nell’Encyclopedie ne tesse un elogio entusiastico.”
Anche in questo secolo quindi non c’è l’egemonia incontrastata di una sola filosofia, ma l’intrecciarsi di varie tematiche e problematiche che certamente vedranno il prevalere, per un lungo periodo, della filosofia di Newton ma che, allo stesso tempo, alimenteranno e nutriranno quelle correnti di pensiero che, prendendo le mosse essenzialmente da Leibniz, confluiranno, agli inizi del secolo seguente, in un’aspra critica del meccanicismo stesso (senza più alcuna distinzione sul tipo di meccanicismo).
RIVOLUZIONE FRANCESE, SCUOLA E SCIENZA
La Rivoluzione Francese ebbe il merito di iniziare un’opera di modernizzazione dell’Europa tirandola fuori da un Regime spartitorio di ogni cosa, e prima di tutto dell’individualità della persona, di Monarchie assolute e Chiesa. Due regimi corrotti che da secoli lavoravano insieme per affermare quovis modo il loro potere sulla enorme massa dei cittadini che non erano neppure tali ma solo carne da lavoro e da macello. I Paesi che riuscirono a seguire lo spirito della Rivoluzione piano piano si andarono liberando delle palle al piede di nobiltà e clero per avanzare sui terreni civili e sociali. Altri continuarono a subire ogni angheria per qualche decennio, in alcuni Paesi fino ad oggi e non si sa fino a quando ancora.
Come ogni momento creativo e, poiché investe grandi masse di persone, sacro, dell’attività dell’uomo la Rivoluzione francese ebbe momenti di degenerazione, di profittatori, di voltagabbana, di veri e propri maniaci. Ma ciò non toglie all’intera avventura il profondo merito che annunciavo e per il quale non smetterò, e nessuno dovrebbe mai smettere, di essere grato a questa impresa collettiva.
I termidoriani segnarono un lungo periodo della Rivoluzione. Per entrare nell’argomento che ho l’intenzione di cominciare a trattare, l’impulso alla ricerca scientifica che venne dalla Rivoluzione, inizio proprio da qui riportando un passo di un lavoro di Furet e Richet, La Rivoluzione Francese (Laterza 2003) che si occupa della base indispensabile per ogni progresso, la scuola:
I Termidoriani non sono soltanto – e del resto non tutti – uomini avidi di denaro e di piacere, e nutrono anzi due. profonde passioni politiche, l’odio per i nobili e l’anticlericalismo. Tutto il loro passato lo dice chiaramente, ed anche il loro presente. Contro i nobili ricorrono ai cannoni anche a dispetto della Costituzione che hanno varato, e contro i preti credono nella forza dell’istruzione, come tutto il XVIII secolo: il popolo è prigioniero dei suoi vecchi pregiudizi perché è ignorante e abbandonato agli uomini della superstizione. Bisogna dunque repubblicanizzare l’insegnamento, fondando un’istruzione pubblica che diffonda i Lumi.
Al vertice delle nuove istituzioni destinate a formare e gestire lo spirito pubblico, c’è l’Istituto di Francia, creato durante l’ultima seduta della Convenzione con la grande legge del 3 brumaio anno IV (25 ottobre 1795). Questo grande corpo scientifico,che deve la propria esistenza alla Costituzione, come il Direttorio e i Consigli, rappresenta per così dire una specie di terzo potere spirituale. […]
L’Istituto diviso in tre classi che coronano l’intero corpo delle discipline – scienze fisiche e matematiche, letteratura e belle arti e, grande novità, scienze morali e politiche – ha quindi un’importante ruolo culturale e politico, come dimostrerà l’organizzazione del 18 brumaio. Tempo addietro, nei pochi mesi che Bonaparte ha trascorso a Parigi fra l’Italia e l’Egitto, ci si meravigliava «di vederlo cosi timido, inoperoso e circospetto, sempre all’Istituto e tutto preso da sua moglie, dalle carte geografiche e dalle poesie di Ossian». Ma la sua frequenza all’Istituto è soltanto uno scaltro pellegrinaggio. Eletto nel 1797 dai suoi colleghi, i grandi baroni della scienza e della Repubblica, al posto di Carnot, escluso, egli diventa un eroe di statura antica; non è più soltanto una spada, ma anche una mente, e del resto non perde occasione per dire «La mia religione è quella dell’Istituto». Il fatto è che, riunendo l’élite intellettuale dell’epoca, l’Istituto dà il cambio alle accademie del XVIII secolo, e diventa in certo modo il conservatorio della tradizione illuminista, cristallizzata in una comune visione del mondo, quella degli «ideologi». Tutti medici, filosofi o letterati, raramente costoro sono uomini di genio; ma i più eminenti […] formano una pleiade di spiriti curiosi dell’ignoto e del nuovo. Tutti seguaci di Condillac, essi respingono le «idee innate» di Descartes, rifiutano qualunque spiegazione metafisica della conoscenza umana, e vogliono fondare una scienza della formazione delle idee partendo dalle sensazioni, donde il loro nome, estendendo questo razionalismo sperimentale a quella ch’essi considerano la scienza del costume e del comportamento umano […].
L’ottimismo di questi precursori del positivismo si fonda sul progresso delle scienze liberate da qualsiasi «presupposto» metafisico. A coloro che nel 1796 lo accusano di spiegare il «sistema del mondo» escludendo l’intervento della provvidenza, Laplace ribatte che quest’ipotesi non gli è stata necessaria. I grandi scienziati dell’epoca – matematici come Lagrange e Monge, chimici come Berthollet, Chaptal, Fourcroy e Darcet, naturalisti come Lamarck, Cuvier e Geoffroy Saint-Hilaire, medici come Pinel e Bichat – non sono tutti necessariamente materialisti, ma i loro studi e le loro scoperte suffragano e divulgano una concezione dell’universo troppo nuova per non riuscire sospetta alla religione e alla tradizione.[…]
L’idea di un’istruzione pubblica destinata a liberare il popolo. dalla superstizione risale alla Convenzione, ai programmi di Condorcet e di Le Peletier e a una legge del 30 frimaio anno II (20 dicembre 1793) sulle «prime scuole» quelle cioè che oggi chiameremmo scuole elementari. Ma le sue più importanti articolazioni furono approvate dopo la caduta di Robespierre e applicate sotto il Direttorio ed è quindi ai Termidoriani che ne spetta la paternità.
I principi cui si ispira sono molto semplici. Il nuovo insegnamento è pubblico e laico, ed esclude perciò sia l’antico monopolio della Chiesa sia il carattere confessionale dell’istruzione impartita. La Chiesa naturalmente è libera di mantenere i propri istituti scolastici, ma le scuole della Repubblica accessibili a tutti i cittadini e agnostiche, godono dell’inestimabile sostegno dello Stato. Quali scuole? Mentre le leggi dei Montagnardi riguardavano soprattutto l’insegnamento primario, l’orientamento termidoriano è più borghese, più destinato a formare i rampolli dei possidenti che a dirozzare la popolazione contadina, ed è condizionato inoltre da ragioni economiche che, poiché non si può fare tutto in una volta danno la priorità all’istruzione delle élites.
La grande legge è la stessa che il 3 brumaio anno IV crea l’Istituto: rimangiandosi in parte le sue vecchie promesse troppo democratiche e troppo costose, la Convenzione prevede soltanto una scuola ogni due o più Comuni, e soprattutto non è lo Stato che stipendia l’insegnante, costretto a vivere del contributo pagato dagli allievi e di un’eventuale indennità del Comune. Nulla si dice dell’obbligo scolastico, sottolineato nel 1793. La Convenzione termidoriana, al contrario, organizza accuratamente l’insegnamento secondario e superiore. Questi due termini presi dal vocabolario moderno sono peraltro assai poco adeguati alle concezioni dell’epoca, giacché le «scuole centrali» previste dalla legge del 24 febbraio 1795 al posto dei collegi dei Gesuiti e degli Oratoriani dell’Ancien Régime, in ragione di una per ciascun dipartimento, sono in realtà una via di mezzo fra le scuole secondarie e quelle superiori del giorno d’oggi. I corsi scolastici previsti dalla legge sono suddivisi in tre sezioni successive: la prima, dai dodici ai quattordici anni, comprende disegno, scienze naturali e lingue antiche e moderne; la seconda, dai quattordici ai sedici anni, scienze (matematica, fisica e chimica); la terza, infine, dai sedici anni in poi, ciò che il testo di legge definisce «grammatica generale» fondata su una teoria del linguaggio e una logica ispirate alla psicologia sensistica degli ideologi, ossia lettere, storia (in cui è sempre compresa la geografia) e diritto. I corsi sono facoltativi e generalmente a carico del dipartimento, e i professori vengono scelti fra i candidati abilitati da una giuria d’istruzione. Molto liberale, e anzi forse anche troppo, questo sistema ammirevolmente innovatore sanziona molte delle rivendicazioni culturali del secolo, quali la laicità, la promozione delle scienze, la supremazia della lingua francese sulle lingue morte, la filosofia.
Salendo ancora, v’è tutto un sistema di istituti superiori, creati anch’essi dalla Convenzione termidoriana, destinati alla formazione degli specialisti e all’incentivazione della ricerca: il Conservatorio delle arti e mestieri, la Scuola dei servizi pubblici per l’esercito, la marina e il genio civile, che diventerà l’odierna Ecole polytechnique; tre scuole di medicina – a Parigi, Lione e Montpellier -, la Scuola normale superiore destinata a formare i professori, la Scuola di lingue orientali il Conservatorio di musica, il Museo e l’Osservatorio. Questo sistema, coronato dall’Istituto di Francia, è indubbiamente troppo concentrato a Parigi e insieme incompleto, giacché dopo le scuole centrali nulla è previsto per le lettere e per diverse scienze. L’avvenire di molti istituti superiori, creati nel 1794-95 dimostrerà comunque ampiamente l’importanza dell’opera dei Termidoriani.
Divenuti direttoriali, i Termidoriani dovettero d’altronde applicare le leggi varate. Lo sviluppo dell’insegnamento primario fu compromesso dalle loro stesse reticenze. Mal retribuiti dal contributo degli scolari o dal Comune i maestri scarseggiano e sono spesso mediocri, e la mancanza dell’obbligo scolastico li pone in certo modo alla mercè dei genitori, che generalmente, da bravi contadini, decidono di «fare come si è sempre fatto», ossia di destinare i propri figli ai lavori agricoli. A che serve del resto un maestro che non insegna il catechismo e la religione e che non prepara i ragazzi alla prima comunione? La scuola privata, spesso tuttora, esistente, ha dalla sua il vantaggio della tradizione. Cosi, per mancanza di denaro, di tempo e di convinzione il tentativo del Direttorio cozza contro la diffusa indifferenza del pubblico, e otterrà qualche risultato solo dopo il 18 fruttidoro, quando il regime comincerà a contrastare localmente la concorrenza, della scuola privata. […]
In ciascun dipartimento furono invece create le «scuole centrali» previste dalla legge. […] Queste scuole ebbero spesso maestri illustri […] Il sistema si rivelò però eccessivamente liberale e ambizioso; molti allievi frequentavano un solo corso, e quasi tutti, invece di seguire la trafila, enciclopedica dei sei anni ripartiti in tre corsi successivi, si suddivisero fra lettere e scienze, segnando cosi sin d’allora la profonda divisione moderna. D’altra parte il livello dell’insegnamento era spesso troppo elevato per quell’uditorio troppo libero e cosi inegualmente preparato. I Consigli del Direttorio cercarono pertanto di restituire alle scuole centrali il loro vero carattere di scuole secondarie, suggerendo la creazione, al livello successivo, di cinque licei e di alcune scuole di medicina che avrebbero favorito il decentramento dell’insegnamento superiore. Come in molti altri settori, essi spianarono cosi la strada alle riforme del Consolato e dell’Impero.
Una buona parte della gioventù borghese – e soprattutto le ragazze – continuerà però a frequentare le scuole secondarie private o ad essere affidata alle cure di precettori benpensanti, giacché molti capifamiglia della buona società, anche se leggono Voltaire, per i propri figli e le proprie mogli preferiscono affidarsi al sostegno morale delle certezze religiose, il che conferisce alla riforma scolastica termidoriana un carattere ancora più rivoluzionario. Il fatto che questo sistema educativo largamente aperto alla ricerca più moderna, pur abolendo a vantaggio dello Stato il monopolio clericale e lasciando il più ampio spazio alle scienze e allo spirito scientifico non abbia raggiunto i suoi obiettivi più immediati né salvato il regime ha un’importanza molto relativa, giacché ha fornito alla Francia borghese delle basi ben altrimenti durevoli.
Con tutti i limiti qui descritti, la politica scolastica, l’allargamento dei fruitori dell’istruzione, la progressiva conquista della laicità contro le spiegazioni irrazionali e metafisiche dei fatti naturali, a fianco di nuove condizioni economiche, saranno alla base della grande fioritura scientifica francese nel periodo immediatamente successivo alla Rivoluzione.
Agli alti livelli dell’elaborazione scientifica il Settecento aveva rappresentato l’accettazione dell’immagine scientifica del mondo elaborata da Newton. Gli scienziati avevano lavorato per ampliare quell’immagine e per conciliarla con quanto di nuovo veniva scoperto sperimentalmente. Dal punto di vista della produzione scientifica non si ottenne quanto l’esaltazione della scienza avrebbe fatto sperare ma si gettarono le basi per l’esplosione dell’Ottocento. Anche se vi fu un’epoca di dittatura della matematica, esercitata da D’Alembert, Lagrange e Laplace, se nacque la chimica moderna con Lavoisier, se con Buffon, Lamarck e Diderot iniziò a definirsi l’ambito della biologia e dell’evoluzione organica. A tale proposito afferma Bernal:
Il confluire di diversi aspetti dell’evoluzione sociale e tecnico-scientifica non può evidentemente essere attribuito a una causa unica. Quanto più da vicino esaminiamo i fili che legano scienza, tecnica, economia e politica, tanto più intricati essi ci appaiono nel quadro del processo generale di trasformazione della civiltà. È questo un periodo cruciale nella storia dell’umanità: è ora – e solo ora – che si ha una svolta decisiva nel dominio dell’uomo sulla natura, con la duplice sostituzione della macchina multipla al posto della mano dell’uomo, e della forza del vapore al posto della forza umana e animale e delle forze incostanti e localizzate del vento e dell’acqua. E le due trasformazioni fondamentali avvenute nei secoli XVI e XVII – presupposti essenziali di quelle del XVIII – erano state la nascita di una scienza sperimentale quantitativa e dei metodi capitalistici di produzione, fenomeni originariamente separati. Le maggiori applicazioni pratiche della scienza e lo stimolo più forte al progresso scientifico si erano avuti nel campo della navigazione, che era un complemento indispensabile dell’attività e del progresso commerciale, ma che era solo indirettamente legata con la produzione. Minore utilità pratica immediata per il miglioramento della manifattura era derivata dal grande sforzo degli scienziati del XVII secolo, riuniti nelle loro società e accademie. La fine del XVIII secolo fu invece caratterizzata dal confluire delle innovazioni scientifiche e capitalistiche, dalla cui interazione si liberarono forze che più tardi avrebbero trasformato sia il capitalismo che la scienza, e insieme il corso stesso dell’umanità.
Le premesse all’innovazione nell’ambito della ricerca in Francia, si erano avute con le Scuole Militari in cui fu possibile realizzare una feconda intersezione tra scienza e tecnica con il grande impegno di Coulomb e Lazare Carnot che imposero nei loro insegnamenti elevati standard di precisione. Si seguiva qui una sorta di cammino alla rovescia di quanto avvenuto in Gran Bretagna dove la scienza era al seguito dei ritrovati tecnici. Ora, dalle elaborazioni teoriche della meccanica razionale, si tentava un avvicinamento alle realizzazioni pratiche. Ed il fenomeno non nasceva per qualche elaborazione a tavolino ma per la spinta di una sempre più intraprendente borghesia che guardava oltre Manica e si sentiva ingabbiata da regole troppo antiquate e paralizzanti. E le scuole politecniche avevano proprio questa funzione, quella di preparare tecnici e scienziati di prim’ordine (tra i quali vi furono vi furono personalità come Henri-Louis le Chatelier, Émile Clapeyron, Auguste Comte, Michel Chasles, Sadi Carnot, Gustave Coriolis, Augustin Louis Cauchy, Augustin Fresnel, François Arago, Claude-Louis Navier, Siméon-Denis Poisson, Joseph-Louis Gay-Lussac, Étienne-Louis Malus, Jean-Baptiste Biot). In queste scuole erano stati reclutati come insegnanti gli scienziati più prestigiosi di cui la Francia disponeva (all’École, tra gli altri: Monge, Berthollet, Lagrange, Laplace, Ampère) ed il loro era un ruolo di servizio allo Stato, erano i primi scienziati che diventavano dei professionisti a cui oltre all’obbligo di istruire era delegato quello di scrivere libri e trattati e rendiconti delle lezioni.
IL PERIODO NAPOLEONICO
L’uscita napoleonica della Rivoluzione ha caratteri di rilievo che vengono ben descritti da Baracca e Livi:
La società napoleonica si configura come vera e propria società tecnocratica, che valorizza la funzione sociale e produttiva dell’attività scientifica, inquadrandola organicamente nelle strutture statali dell’educazione. Gli scienziati, divenuti ormai professionisti, funzionari statali, sono tenuti in grande onore e assumono cariche importanti. La loro situazione non è assolutamente confrontabile con quella degli scienziati inglesi dell’epoca, spesso ridotti in miseria e senza protezione statale. Alla centralizzazione della ricerca scientifica nel quadro dell’alta burocrazia creata da Napoleone, e concentrata a Parigi, corrisponde una più accentuata divisione del lavoro. Nasce la specializzazione scientifica. L’unità filosofica illuministica si frantuma di fronte a nuove esigenze di integrazione della scienza nel processi produttivi e nel corpo sociale. Le branche scientifiche si rendono autonome […] nascono la pura matematica, la pura analisi, la pura geometria; la fisica-matematica si separa dalla matematica, la chimica dalla fisica cosi come viene riconosciuta l’autonomia della termodinamica (da Fourier e Sadi Carnot) e dell’elettrodinamica (da Ampère). […] Si configura cosi un rapporto di tipo nuovo tra la scienza e l’attività produttiva, che va ben al di là dell’ideologia illuministica. La scienza deve ora attestarsi su canoni metodologici che ne legittimino la ricerca di nuovi standards di esattezza e di rigore, sia manuali che teorici, giustificando lo studio delle leggi naturali e delle loro applicazione non più in base all’illusione illuministica di essere direttamente uno stimolo per la produzione, ma piuttosto asserendo l’autonomia e la necessità di tale ricerca in quanto valida in sé e destinata pertanto ad avere prima o poi delle applicazioni utili. L’ispirazione diretta ai problemi che nascono nel mondo della produzione viene anzi sistematicamente rivendicata dai fisici dell’École. La filosofia funzionale a questi sviluppi sarà quella del positivismo, che si instaura di fatto come atteggiamento generale e come metodo di lavoro nell’ambito dell’École, prima che i suoi canoni vengano ufficialmente enunciati da Comte, anch’egli appartenente non a caso al medesimo ambiente.
Il positivismo, con il culto del fatto scientifico, lo studio dei fatti sperimentali e la ricerca delle loro leggi matematiche, traduce l’esigenza di staccarsi definitivamente dalle ipotesi metafisiche del passato, la richiesta di obiettività e di rigore imposta dalla diffusione delle conquiste tecniche e di un modo di produzione che fa di esse un cardine del suo funzionamento.
Malgrado la specializzazione delle nuove branche, però, la meccanica – pur cessando di delineare l’intero orizzonte della «filosofia naturale» – rimane un quadro di riferimento necessario per la conoscenza razionale e pratica della realtà. La limitazione alle sole azioni rettilinee di forze centrali agenti a distanza (che è così esplicita, ad esempio, nei fondatori francesi dell’elettrodinamica) non è vista in alcun modo come un’ipotesi, poiché un suo uso in tal senso sarebbe anzi incompatibile con l’esigenza positivistica di attenersi ai fatti; tale limitazione costituisce piuttosto uno schema «a priori», in senso kantiano, una proprietà inerente ai fenomeni naturali, che garantisce la possibilità stessa di impostare degli esperimenti e di estrarne correttamente i risultati in modo rigoroso, assicurando cosi uno stretto legame tra le due fasi del lavoro scientifico come si vedrà ad esempio con particolare chiarezza nell’opera di Ampère.
E’ da osservare che questi caratteri saranno mantenuti anche dopo la caduta di Napoleone, durante la Restaurazione, almeno fino al 1830. La spinta iniziale era stata così imponente che per vari anni ancora si conseguirono risultati molto brillanti. Era però venuto meno lo slancio che la borghesia aveva impresso relativo all’uso di quanto la scienza realizzava ed una traccia evidente di ciò la possiamo ritrovare nei lavori di Sadi Carnot che rimasero praticamente ignorati in Francia. Ma vi è anche un altro aspetto, sottolineato da altri autori, secondo il quale la politica, gli affari ed anche il fare i letterati, era diventato più attraente per il successo sociale che non il fare lo scienziato. A ciò si può certamente aggiungere che il forte accentramento unito all’insopportabile burocrazia creò delle rigidità che non misero gli scienziati in grado di evolvere come i rapidi progressi nei vari campi della ricerca scientifica richiedevano.
Questa premessa dovrebbe aiutare a capire il clima in cui ci si muove e a far meglio comprendere il lavoro scientifico di alcuni degli allievi dell’École, a cominciare da Ampère.
BIOGRAFIA SCIENTIFICA DI ANDRÉ-MARIE AMPÈRE
André-Marie Ampère nacque nel 1775 in un paesino vicino Lione. Non fece studi regolari e suo padre lo volle educare secondo i principi dell’Émile di Rousseau. Ebbe lezioni private e fu in gran parte autodidatta. Mostrò fin da giovane grandi abilità per il calcolo ed interessi molto vivi per i fenomeni naturali. Lesse moltissimo tutto ciò di cui disponeva con particolare interesse per l’Encyclopédie i cui autori studiò organizzandone la lettura addirittura mettendoli in ordine alfabetico. Il latino che non lo aveva interessato quando era ancora giovanissimo, lo interessò ai 16 anni quando si rese conto che era l’unico modo per leggere le opere di Daniel Bernouilli, Newton ed Euler.
La libertà che suo padre, pur fervente cattolico, concesse al figlio, permise a quest’ultimo di apprezzare fino in fondo lo spirito dell’89 e quindi il grande valore che deve essere assegnato alla libertà ed alla scienza per l’emancipazione dell’uomo e delle nazioni. Un breve scritto di Ampère, una lettera al suo amico Gosse del 1817, epoca buia di Restaurazione, può far intendere lo spirito positivo che animava Ampère che si accompagnava ad un sincero auspicio di miglioramento, attraverso la conoscenza, delle condizioni di vita e di lavoro dell’uomo:
Non si devono temere lo sviluppo dell’industria e le continue invenzioni di macchine e di procedimenti per abbreviare il lavoro, ecc. Man mano che il lavoro di un medesimo numero di uomini produce di più, i prodotti diminuiscono di costo e il loro uso si estende di classe in classe. Bisogna incoraggiare questo progresso fino a quando l’ultimo agricoltore abbia buoni alimenti, buoni vestiti, abitazioni salubri, ecc. Auguriamoci che queste idee si sviluppino e si moltiplichino. Si dice che allora l’agricoltore non vorrà più lavorare: l’esperienza prova il contrario. Il contadino, l’operaio spagnolo o il bretone passano la metà del loro tempo coricati nella loro sudicia capanna. Quelli invece del Delfinato o della Normandia, impiegano ogni minuto della loro giornata per non perdere neppure una parte del benessere a cui sono abituati. Inoltre in una carestia questi soffrono soltanto una diminuzione di godimento, mentre quelli che non hanno mai saputo procurarsi altro che lo stretto necessario muoiono di fame quando le circostanze li privano delle loro risorse. Più gli uomini producono, più le tasse sono considerevoli e facili da esigere, più la massa della nazione è felice, più i delitti sono rari. Questa condizione superiore a quella odierna sarà il sicuro risultato del cammino sempre accelerato dello spirito umano. Paragonate l’Europa dei tempi [del Quattrocento] con l’Europa moderna e da quanto si è raggiunto in questo intervallo di tempo immaginate quello che si potrà ottenere in un eguale periodo a partire da oggi. Man mano che si avanza, la velocità cresce, avviene come per un corpo che cade. Ma l’azione dei governi può ancora facilitare questo progresso; ringraziamo quelli che lo comprenderanno.
Che queste opinioni rimangano fra […] noi; esse mi farebbero lapidare e io non potrei vedere l’aurora del giorno in cui se ne annuncerà la realizzazione. Eccoci già liberati dai due grandi flagelli che hanno rischiato di soffocare la Francia: lo spirito giacobino che voleva soltanto pane e ferro e lo spirito militare, che richiedeva uomini e ricchezze per coloro che distruggevano invece di produrre.
A. Ampère.
Nel 1796, dopo tre anni di completa apatia dovuta al dolore per la morte del padre, Ampère iniziò a dare insegnamenti privati (matematica, chimica e lingue) a Lione. Qualche anno prima, nel 1793, aveva perso in modo drammatico suo padre che, giudice di pace a Lione, era stato condannato a morte perché la città dove esercitava si era ribellata alla Convenzione che aveva riconquistato la città ed esercitato una violenta repressione. Lo consolò una donna, Julie Caron, con la quale nello stesso 1896 si sposò. Nel 1801 fu assunto come professore di fisica-chimica nella scuola secondaria di un paesino a 70 km da Lione. Questa scuola era chiamata centrale ed era una delle creazioni della Rivoluzione. Nel 1801 però il ministro dell’Istruzione di Napoleone aprì un’inchiesta su tali scuole e nel 1802 le fece chiudere trasformandole in ordinari licei perché, a suo giudizio, non coordinate con le scuole primarie, troppo libere e scarse di insegnamento religioso. Nel 1804 Ampère ebbe un nuovo grandissimo dolore per la perdita della sua amatissima Julie che lo lasciò solo con un figlio e con varie meditazioni metafisico-religiose. Nel 1806 finalmente Ampère, per interessamento di Delambre, passò a fare l’assistente di analisi matematica all’École Polytechnique. Quest’ultimo suo passaggio è importante perché porta Ampère a Parigi, a contatto con l’ambiente culturale più vivo di Francia.
Già a partire dal 1801 Ampère aveva iniziato la sua produzione scientifica scrivendo di matematica. Nel 1802 fu stampato il suo primo lavoro, Considerazioni sulla teoria matematica del gioco, che impressionò Delambre che volle conoscere il giovane divenendone il protettore. Questi anni, fino al 1815, saranno per Ampère di grande impegno matematico con incursioni importanti in ambito chimico ed anche con un lavoro del 1815 in cui studiava le leggi della rifrazione(1). Pubblicò vari lavori che lo fecero conoscere ed apprezzare negli ambienti scientifici, fino a riconoscimenti ufficiali come la sua nomina a membro dell’Académie des Sciences, a segretario del Bureau des Arts et des Métiers e a professore di Analisi matematica e Meccanica all’École. Va comunque detto che Ampère non pubblicava tutto ciò che trovava e realizzava. Dalle sue Lettere sappiamo che egli ottenne molti risultati prima di altri e che sono attribuiti ad altri perché questi ultimi li pubblicarono pur avendoli elaborati in modo indipendente ma successivamente(2). La sua generosità e curiosità faceva spiegare cose agli amici senza che egli ne traesse benefici. Inoltre, dato un problema, esso perdeva ogni attrattiva per Ampère nel momento in cui aveva trovato la sua soluzione.
Ma il corpo delle opere per cui Ampère è diventato, con merito, famoso doveva ancora iniziare ad essere scritto e ciò avvenne dopo due comunicazioni di François Arago all’Académie des Sciences il 4 e l’11 settembre 1820.
LA NATURPHILOSOPHIE ED OERSTED
(per comodità del lettore riporto quanto già trattato altrove, con qualche approfondimento)
Gli eccessi della Rivoluzione e gli ideali dell’Illuminismo esportati non già da D’Alembert e Diderot ma dagli eserciti di Napoleone, provocarono reazioni importanti in tutta Europa anche in ambito di pensiero(3). L’Ottocento è il secolo del Romanticismo, ed in particolare, per ciò che ci riguarda ora, di Schelling (1775 -1854), il fondatore della Naturphilosophie, la filosofia della natura. Tra il 1797 ed il 1801, Schelling scrisse 4 lavori(4) in cui sviluppò le sue idee
Secondo Schelling il meccanicismo fisico non rende ragione dell’esistenza della natura, contrariamente al dinamismo che egli ricava da Kant e che ha ascendenti in Boscovich. La concezione meccanicista di materia come un qualcosa di inerte fino a che su di essa non agiscono forze, entità diverse e separate dalla materia è, secondo Schelling, l’ammissione di una discontinuità tra materia e spirito (tra natura e uomo) che non corrisponde alla unità originaria di queste due entità, per esempio, nell’organismo vivente. Schelling sostiene che è lo spirito (le forze) che si organizza in materia e pone quindi le forze, agenti tra punti inestesi (alla Boscovich), con i loro “conflitti e trasformazioni” alla base dell’esistenza del mondo (dinamismo fisico). Non c’è più materia allora ma c’è una particolare modificazione di una determinata zona dello spazio dovuta appunto ai conflitti ed alle trasformazioni delle forze (spirito) eterne e preesistenti. Questo rifiuto netto del meccanicismo, e più in generale del metodo scientifico, non nasce casualmente in questo periodo.
Le differenti scoperte in ambito elettrico e magnetico, che il meccanicismo non aveva ancora spiegato esaurientemente, avevano aperto campi di indagine e di polemica in cui si inserirono efficacemente le speculazioni romantiche nella loro offensiva generale contro il meccanicismo. Certamente al culmine del meccanicismo, quando l’azione istantanea a distanza lungo la congiungente gli «oggetti» era alla base di tutte le teorie fisiche, nessuno avrebbe pensato di ottenere un qualche risultato progettando esperienze che si ponevano a priori in contrasto con le premesse di principio ed in particolare con quel tipo di azione. È quindi proprio sotto l’influenza ideologica della Naturphilosophie che il fisico e chimico danese Hans Christian Öersted (1777-1851), professore all’università di Copenaghen dal 1806, progettò ed effettuò una memorabile esperienza che scosse profondamente l’edificio meccanicista(5). Per la prima volta, dopo più di 130 anni di rassicuranti azioni ‘rettilinee a distanza’, veniva evidenziata una azione totalmente differente: un filo conduttore, se disposto parallelamente ad un ago magnetico, vede l’ago ruotare di 90º e disporsi perpendicolarmente al filo, quando in esso viene fatta circolare corrente.
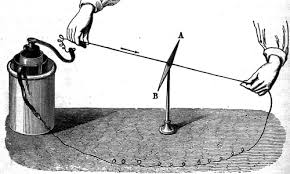
Esperienza di Oersted
Questo tipo di azione si svolge su di un piano perpendicolare alla congiungente filo – ago e consiste in una rotazione dell’ago medesimo risultando, come dice Oersted, ‘circolare’. Oersted, nel condurre l’esperienza, muove l’ago nello spazio circostante il filo e si accorge che, se la rotazione avviene in un senso con l’ago disposto sotto il filo, essa avviene in senso opposto se si dispone l’ago sopra il filo. Per Oersted quindi, le forze magnetiche sono distribuite nello spazio che circonda il filo e, data la simmetria degli spostamenti dell’ago, conclude che le forze magnetiche sono costituite da cerchi “poiché è nella natura dei cerchi che movimenti da parti opposte debbano avere opposte direzioni” (oggi diremmo che le linee di forza del campo magnetico intorno ad un filo rettilineo percorso da corrente, sezionando il filo con un piano ad esso perpendicolare, hanno la forma di circonferenze concentriche al filo).
Questo tipo di azione non era più riconducibile alle forze centrali. Sono proprio le forze secondo un moderno modo di vedere, che riempiono tutto lo spazio e quindi che esistono sia lungo la congiungente filo-ago sia lungo la normale a questa congiungente che rendono possibile la deviazione dell’ago. Lo stesso Öersted, dopo aver premesso che:
«all’effetto che ha luogo nel [filo] conduttore e nello spazio circostante, daremo il nome di conflitto elettrico»,
e dopo essersi accertato degli effetti di simmetria:
«se si colloca il filo conduttore in un piano orizzontale sotto l’ago magnetico, si hanno gli stessi effetti come se il filo fosse posto in un piano al di sopra dell’ago, però in direzione opposta»,
sosteneva:
« … Il conflitto elettrico non è racchiuso nel conduttore ma, come abbiamo già detto, è al medesimo tempo disperso nello spazio circostante, e ciò è ampiamente dimostrato da tutte le osservazioni fin qui fatte… ».
Riferendosi poi all’effetto di simmetria da lui riscontrato nel disporre l’ago magnetico al di sopra o al di sotto del filo percorso da corrente diceva:
« … In maniera simile è possibile dedurre da quanto abbiamo osservato che questo conflitto agisce circolarmente perché questa sembra essere una condizione senza la quale è impossibile che la medesima parte del filo di congiunzione, che quando sta sotto il polo magnetico lo fa spostare ad est, lo fa spostare invece ad ovest quando è posta sopra di esso. Perché è nella natura dei cerchi che moti in parti opposte abbiano direzioni opposte… ».
La Naturphilosophie aveva la sua base sperimentale e l’esperienza di Öersted, se da una parte si opponeva alle teorie meccaniciste, dall’altra affermava l’esigenza del metodo scientifico (negata da Shelling): le forze o chi per esse preesistono nella «natura» solo se, andandole a cercare, le troviamo. Comunque questa osservazione non fu fatta all’epoca e l’esperienza di Oersted suscitò un interesse ed un fermento di ricerca che tanti risultati avrebbero dato allo sviluppo della scienza.
Il quadro concettuale nel quale questa esperienza irrompeva era quello newtoniano che si era affermato a partire dalla scoperta della gravitazione universale (Newton, 1685). Al di là dell’aspetto matematico (proporzionalità tra masse che interagiscono e dipendenza dall’inverso del quadrato della distanza tra i loro centri), questa legge
sottintende che:
1) l’azione tra le due masse è rettilinea, avviene cioè lungo la retta che unisce i centri delle stesse;
2) l’azione è a distanza, non si ha cioè bisogno di intermediari tra le due masse perché l’azione abbia luogo;
3) l’azione è istantanea, non richiede cioè tempo per propagarsi (essa si propaga quindi con velocità infinita).
Tutto il Settecento, come già detto, visse sotto l’autorevole influsso di Newton e quindi alla ricerca di azioni del tipo di quelle descritte. Così John Michell nel 1750 provò a dare una stessa legge per le forze che si esercitano tra poli magnetici trovando un qualcosa di simile (a parte la definizione dei poli con p):
F = K1.(p1.p2)/r2
(proporzionalità tra ‘poli’ che interagiscono e dipendenza dall’inverso del quadrato della loro ‘distanza’), legge che non funziona e Coulomb ricavò (1785) la legge di forza tra cariche elettriche (a parte la definizione della definizione di carica con q):
F = K2.(q1.q2)/r2
(proporzionalità tra cariche che interagiscono e dipendenza dall’inverso del quadrato della distanza tra i loro centri), legge che funziona solo a condizione di cariche puntiformi ed a grande distanza, …. Insomma tutti i fisici tentavano di trovare leggi alla Newton e nel far ciò avrebbero certamente disposto i loro strumenti di misura ‘tra’ i due oggetti che andavano ad interagire.
Questo quadro interpretativo, per la verità poco fecondo, venne sconvolto dall’esperienza di Oersted che, come già detto, era un convinto sostenitore di Schelling che riteneva le forze essere presenti dappertutto con i loro conflitti e trasmutazioni.
Occorre a questo punto dire che dall’esperienza di Oersted avevano un ambiente di facile accettazione per la difficoltà più generale che la pila ed il galvanismo avevano rispetto alla fisica di Newton. Inoltre quell’esperienza fu possibile proprio perché era stato realizzato quel generatore di corrente continua che è la pila. Disponendo di un tale generatore è possibile mostrare effetti altrimenti impensabili. Naturalmente non bastano gli apparati sperimentali, occorre anche essere guidati da un pregiudizio, in questo caso dal conflitto di forze.
Oersted mostrò, in linguaggio moderno, che una corrente elettrica provoca effetti magnetici e Faraday mostrerà che il magnetismo produce elettricità. Da questo momento il magnetismo diventa un capitolo della più generale scienza elettromagnetica (resta sempre lo studio dei fenomeni legati ai materiali magnetici ma sarà piuttosto un problema di struttura della materia). Finché la luce non sarà inglobata nel più generale elettromagnetismo, rendendo l’ottica un suo capitolo. E la misura della sua velocità ci riporterà a vicende meccaniche con conseguenze impensabili ancora alla fine dell’Ottocento.
Il campo di indagine diventò immenso e sarà occupato successivamente dai grandi fisici dell’Ottocento e dei primi del Novecento, tra i quali giganteggiano Ampère, Ohm che formulerà le leggi della corrente fornita da una pila, Faraday, Maxwell, Hertz, W. Thomson, Lorentz, Einstein.
L’INTERVENTO DI AMPÈRE
Tra i primi ad iniziare ricerche per trovare correlazioni tra fenomeni elettrici e magnetici che in qualche modo rendessero meglio conto dell’esperienza di Oersted per cercare di ricondurla nell’ambito delle forze centrali, furono i meccanicisti (Biot, Arago, Ampère ed altri). La memoria di Öersted, come accennato, fu comunicata all’Académie des Sciences di Parigi, il 4 e l’11 settembre del 1820 da François Arago. Immediatamente, nello stesso settembre, partirono le prime ricerche sperimentali degli scienziati francesi. In quello stesso mese ed in quelli immediatamente successivi Ampère lesse all’Académie una serie di note(6) in cui riuscì in un impresa da tutti ritenuta impossibile: quella di ricondurre le forze del tipo di quelle osservate da Oersted al caso delle forze centrali.
Prima di passare ad un qualche approfondimento sull’opera di Ampére è bene osservare che, fra le comunicazioni all’Académie ve ne furono, come vedremo meglio più oltre, due di una certa importanza fatte da Jean Baptiste Biot (1774-1862) e Felix Savart (1791-1841)(7). Anche se non c’è una precisa documentazione scritta, risalente all’epoca delle comunicazioni all’Académie, sulle ipotesi e sugli esperimenti da cui mossero Biot e Savart, che permetta un giudizio critico sul loro contributo alla spiegazione delle «forze di Oersted», i due fisici riuscirono a fornire una determinazione molto accurata della legge di forza tra corrente ed ago magnetico. Alla determinazione di questa legge, nella sua forma integrale definitiva, contribuì anche Laplace come ricorda Biot(8):
… Egli (Laplace) ha dedotto matematicamente dalle nostre osservazioni la legge della forza esercitata singolarmente da ogni tratto di filo su ogni molecola magnetica ad esso esposta. Questa forza è diretta, come l’azione totale, perpendicolarmente al piano formato dall’elemento longitudinale di filo e dalla più breve distanza tra questo elemento e la molecola magnetica sollecitata. La sua intensità, come nelle altre azioni magnetiche è inversamente proporzionale al quadrato di questa stessa distanza.
Come si vede, anche questa è una legge che ha una grande analogia formale con quella di Coulomb e quella di Newton: l’andamento con l’inverso del quadrato della distanza ed il riconoscimento stesso di un’azione a distanza bastano per ora a far intravedere la presenza rassicurante di Newton e ad allontanare lo spettro delle forze « disordinate » ed « in permanente conflitto ».
Il contributo di Ampère (1775-1836), come è stato già detto, fu più preciso e determinante mostrando, come primo risultato, che non solo un ago magnetico ruota in presenza di una corrente ma anche un’altra corrente opportunamente disposta. Nella sua prima memoria del 18 settembre all’Académie annunciò la scoperta delle azioni ponderomotrici tra correnti elettriche, nelle immediatamente successive illustrò meglio il fenomeno con dovizia di particolari, di sperimentazioni diverse, di interpretazioni teoriche. Seguiamo con un poco di attenzione l’opera di Ampére. Egli studiando l’azione che si esercita tra due correnti, da lui stesso scoperto nel settembre 1820, scriveva(9):
... I due conduttori si trovano così paralleli e vicini l’un l’altro su di un piano orizzontale; uno di essi può oscillare intorno alla linea orizzontale passante per le estremità dei due punti di acciaio, e, in questo movimento, esso resta necessariamente parallelo all’altro conduttore (che è) fisso...
Ampére inizia a studiare due conduttori rettilinei disposti parallelamente ed in grado di muoversi parallelamente l’uno rispetto all’altro. In questo caso si ha attrazione o repulsione (a seconda del verso delle correnti nei due fili).
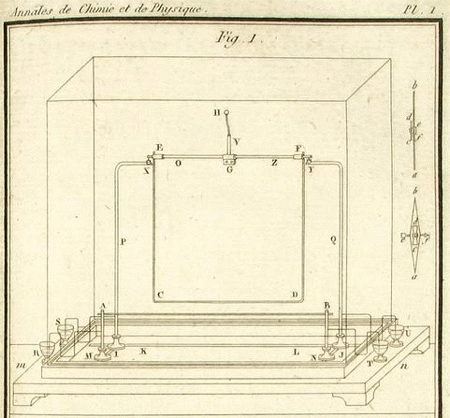
Uno dei primi sistemi ideati da Ampère per studiare le azioni elettrodinamiche tra correnti (bilancia di Ampère). Il conduttore AB è fisso mentre il lato BC della spira BCEF è mobile potendo oscillare lungo l’asse EF, mantenendosi parallelo ad AB. Questa bilancia e le successive mostrate provengono dalla prima memoria di Ampère sulla spiegazione dell’esperienza di Oersted (Mémoire sur les effets des courants électriques, 1820).
Di seguito altri sistemi (bilance) ideati da Ampère.
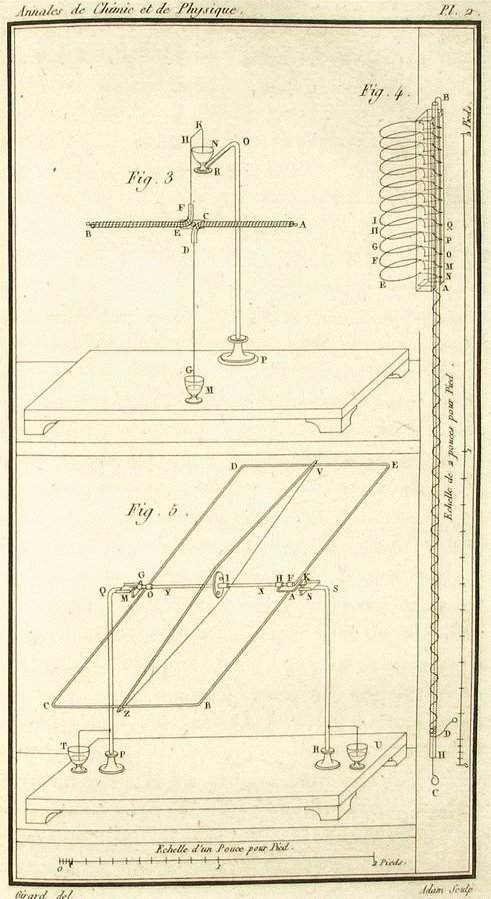
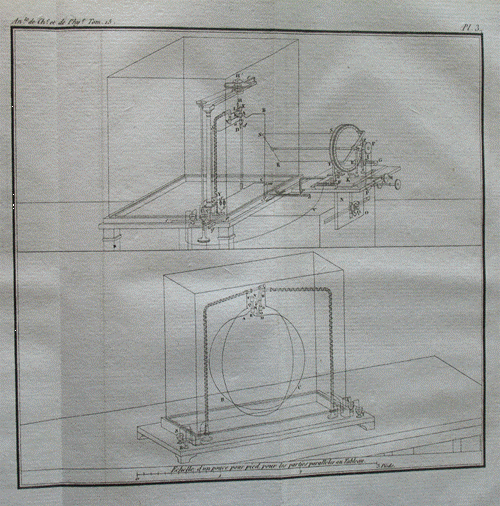
Ancora altri sistemi (bilance) ideati da Ampère.

Ancora altri sistemi (bilance) ideati da Ampère.
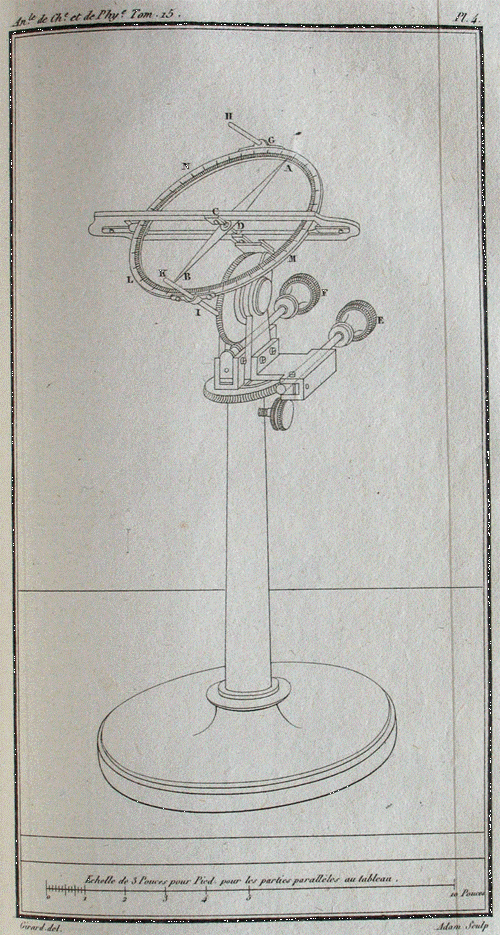
Sistema per impedire all’ago magnetico di sentire l’influenza del campo magnetico terrestre.
Il problema che Ampére aveva bene in mente era però quello della rotazione dell’ago magnetico di Öersted ed allora egli monta l’esperienza in modo da avere un filo rettilineo fisso ed un altro in grado di ruotare su di un piano parallelo al primo(9):
… Se il conduttore mobile, invece di essere costretto a muoversi parallelamente a quello fisso, è libero soltanto di girare su di un piano parallelo a questo conduttore fisso, intorno ad una perpendicolare comune passante per i loro centri, è chiaro che, secondo la legge che abbiamo appena ammesso per le attrazioni e repulsioni delle correnti elettriche, le due metà di ogni conduttore attireranno e respingeranno quelle dell’altro, secondo che le correnti siano concordi o discordi; per conseguenza il conduttore mobile girerà fino a quando esso arriva in una situazione in cui si trovi parallelo a quello fisso, e in cui le correnti siano dirette nello stesso senso: da cui segue che nell’azione mutua di due correnti elettriche l’azione direttrice e l’azione attrattiva o repulsiva dipendono da uno stesso principio e non sono che effetti differenti di una sola e medesima azione.
Ampère riuscì a realizzare un sistema di sospensione di una spira percorsa da corrente con contatti mobili (coppette minuscole ripiene di mercurio) come quella di figura seguente:
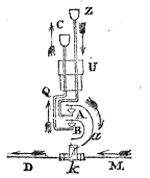
Figura originale di Ampère che compare nella sua memoria
Nella figura si vede che la corrente entrando da Z passa in A dove vi è il primo contatto strisciante della spira. Da qui la corrente entra nella spira (della quale vediamo solo il lato MD), la percorre uscendo in B che è l’altro contatto strisciante della spira. Da B, infine, la corrente torna nel circuito fisso attraverso C. Nella figura seguente è mostrata l’intera spira sospesa al sistema descritto precedentemente:
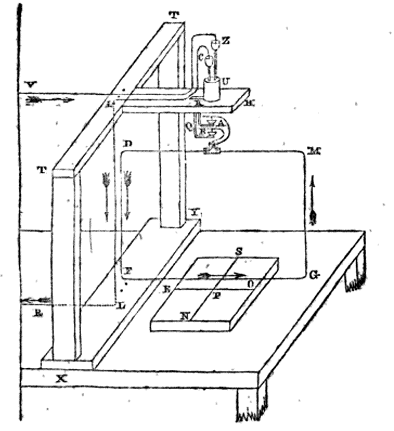
Il sistema realizzato da Ampère per studiare l’azione di un circuito fisso e di una spira sospesa e libera di ruotare. Da Recueil d’observations électro-dynamiques, 1822.
La figura mostra che la corrente del circuito fisso entra in V. Da V va a finire al punto Z che abbiamo visto precedentemente. Segue il circuito precedentemente descritto ZADFGMBC. Da C la corrente ritorna al circuito fisso passando per quella lettera che si legge poco, I , quindi in L, quindi per l’altra lettera che si vede poco chiaramente, R. In questa bilancia la spira può ruotare intorno al sistema di sospensione potendo evidenziare gli effetti di una corrente rettilinea fissa, PL, con una corrente rettilinea, DF, che ora può ruotare con maggiore libertà non avendo vincoli gravitazionali come nella prima figura mostrata.
Nel caso quindi in cui uno dei due conduttori in esame è libero di ruotare esso tende a disporsi parallelamente al primo. In definitiva, secondo Ampère, due correnti non parallele tendono a disporsi parallelamente. Questo primo ragionamento, confortato dall’esperienza, è il nocciolo su cui si impernia tutta l’ulteriore discussione che porterà Ampère ad ammettere una sostanziale identità tra correnti e magneti. Egli dice:
Non è più allora necessario stabilire tra questi due effetti la distinzione che è così importante fare, come vedremo fra poco, quando si tratta dell’azione mutua di una corrente elettrica e di un magnete considerato come si fa ordinariamente in rapporto al suo asse, perché, in questo tipo di azione, i due oggetti tendono a sistemarsi in direzioni perpendicolari tra loro.
L’ipotesi riduzionista di Ampère non può però prescindere da una « teoria » che vada ad interpretare il magnetismo come, appunto, originato da particolari correnti. Ed allora un magnete, ed in particolare un ago magnetico, viene concepito come circondato da correnti che si avvolgono attorno al suo asse risultando perpendicolari a quest’ultimo.
Ampère passa quindi a sottoporre all’esperienza questa ipotesi cominciando a studiare le azioni mutue tra correnti e magneti e tra magneti e magneti:
Esaminerò… l’azione mutua tra una corrente elettrica ed il globo terrestre o un magnete e l’azione mutua di due magneti l’uno sull’altro e mostrerò che esse rientrano l’una e l’altra nella legge dell’azione mutua di due correnti elettriche che ho appena annunciato, concependo sulla superficie e all’interno di un magnete tante correnti elettriche, in piani perpendicolari all’asse di questo magnete, quante si possono concepire linee formanti, senza intersecarsi mutuamente, delle curve chiuse; in modo che non mi sembra molto possibile, dopo il semplice raffronto dei fatti dubitare che non vi siano realmente queste correnti intorno all’asse dei magneti, o piuttosto che la magnetizzazione non consiste che nella operazione per la quale si fornisce alle particelle d’acciaio la proprietà di produrre, nel senso delle correnti di cui abbiamo appena parlato, la stessa azione elettromotrice che si trova nella pila voltaica… .
E questa azione elettromotrice non è rilevabile perché, come osserva Ampère:
… Solamente, poiché questa azione elettromotrice si sviluppa nel caso del magnete tra le differenti particelle di uno stesso corpo buon conduttore essa non può mai… produrre alcuna tensione elettrica, ma solamente una corrente continua rassomigliante a quella che avrebbe luogo in una pila voltaica rientrante su se stessa in modo da formare una curva chiusa [oggi diremmo: pila cortocircuitata, ndr]: è abbastanza evidente… che una tale pila non potrebbe produrre in alcuno dei suoi punti né tensione né attrazioni o repulsioni elettriche ordinarie…; ma la corrente che si stabilirebbe immediatamente in questa pila agirebbe, per orientarla, attirarla o respingerla, sia su un’altra corrente elettrica, sia su un magnete che viene allora considerato come un insieme di correnti elettriche.
E con queste ultime esperienze in connessione con i termini teorici (le ipotesi aggiuntive) Ampère riesce a portare a compimento un’operazione che soltanto un mese prima sarebbe sembrata impossibile: la spiegazione in termini newtoniani dell’esperienza di Öersted. Nel portare a compimento questo «programma » Ampère arriva anche ad una importante conclusione che trascende gli scopi per cui aveva iniziato a lavorare:
E’ cosi che si arriva a questo risultato inatteso, che i fenomeni magnetici sono unicamente prodotti dalla elettricità….
Ecco allora su quali ipotesi Ampère trova la legge di forza tra correnti: il magnete è pensato come un insieme di correnti elettriche nei piani perpendicolari alla linea che unisce i poli. Questa ipotesi è dunque necessaria ad Ampère, e non accessoria come sembra dalla lettura di qualche testo od articolo, per ricavare l’azione ponderomotrice tra correnti, per rendere conto dell’esperienza di Öersted e, infine, per ricondurre le «forze in conflitto» all’ordine newtoniano.
L’introduzione di questa ipotesi spiega bene il perché, contrariamente a due fili percorsi da corrente che tendono a sistemarsi parallelamente, un ago magnetico tende a disporsi perpendicolarmente ad un filo percorso da corrente. Quest’ultimo fenomeno è in realtà analogo a quello dei due fili: sono le correnti che circolano perpendicolarmente al filo e nel far questo portano l’asse del magnete ad essere perpendicolare al filo stesso come mostrato in figura:
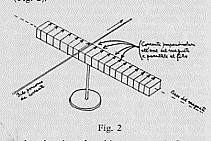
L’esperienza di Oersted nell’interpretazione di Ampère in un disegno mio.
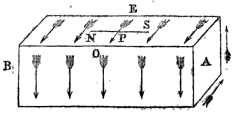
Il disegno originale di Ampère del magnete.
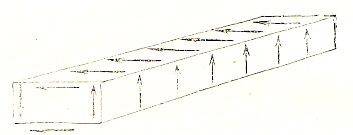
Altro disegno originale
Ampère si rende subito conto però che non è possibile ricavare la legge di forza tra due correnti se non passando attraverso elementi infinitesimi di circuito ed infatti egli trova che:
… L’azione di quelle [correnti] delle quali si possono misurare gli effetti, è la somma delle azioni infinitamente piccole dei loro elementi, somma che si può ottenere con due integrazioni successive, l’una da farsi su tutta la lunghezza di una delle correnti relativamente ad uno stesso punto dell’altra, la seconda da eseguirsi sul risultato della prima integrazione … su tutta l’estensione della seconda corrente…
Anche qui quindi l’espressione della legge che regola l’azione che si esercita tra due correnti elettriche ha il carattere di azione istantanea a distanza tipico della fisica newtoniana. È questo un trionfo di Ampère. I fluidi imponderabili stessi, che la Naturphilosophie con Öersted aveva allontanato dall’indagine fisica rientrano ora di prepotenza sulla scena impregnando di sé non solo la spiegazione dei fenomeni elettrici ma la costituzione stessa della materia.
Da un punto di vista analitico la formula che ci presenta Ampère (Théorie mathématique des phénomènes électro-dynamiques uniquement déduite de l’expérience, 1827) è un capolavoro di “imbroglio fisico-matematico” che, in nome dell’eleganza e semplicità newtoniana ci spaccia come azione centrale quella descritta da(10):
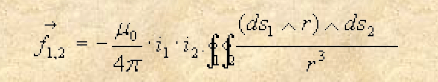
Nella relazione scritta i1 ed i2 sono le correnti che circolano nei due fili, ds1 e ds2 sono gli elementi infinitesimi dei circuiti 1 e 2, r è il raggio vettore da ds1 a ds2
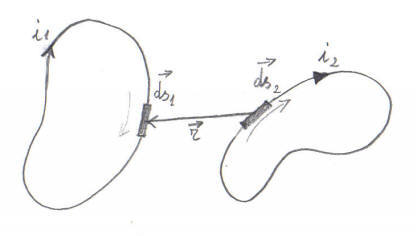
Due circuiti e gli elementi che determinano le attrazioni (in questo caso) tra correnti

Due delle figure originali di Ampère utilizzate per il calcolo della formula appena data. Da Théorie mathématique des phénomènes électro-dynamiques uniquement déduite de l’expérience, 1827.
(questa legge, nella semplificazione di correnti rettilinee, parallele e complanari, è quella nota come azione elettrodinamica tra correnti di Ampère che si studia in ogni corso elementare di fisica: la forza che si esercita su un tratto di filo di

lunghezza s del conduttore è proporzionale, oltre che a tale lunghezza, alle intensità i1 ed i2 delle correnti che fluiscono nei fili ed inversamente proporzionale alla loro distanza r). Provo a spiegare l’imbroglio di Ampère. Nella relazione figura il prodotto tra due correnti e, a meno di costanti, la cosa è formalmente identica a tutte le relazioni che si richiamano alla gravitazione di Newton. Osservando ancora, in modo superficiale, sembrerebbe che l’r che compare al numeratore si debba semplificare con l’r3 che compare al denominatore, di modo che si avrebbe ancora la legge dell’inverso del quadrato. In realtà al numeratore vi è un doppio prodotto vettoriale e vi sono due integrazioni circolari. A conti fatti la relazione non c’entra nulla con quella di Newton, soprattutto perché lo svolgimento dei prodotti vettoriali origina grandezze dipendenti da angoli. E’ facile convincersi che mai Newton avrebbe pensato a forze dipendenti da angoli. Il fatto è che vi era una sorta di religione: non si riusciva a tagliare il cordone con Newton. Solo Faraday, probabilmente perché outsider, proveniente non da ambienti accademici, riuscì nell’impresa e demolì ogni interpretazione newtoniana nell’interpretazione dei fenomeni elettromagnetici.
NECESSITÀ DI INTERPRETAZIONI MICROSCOPICHE: LA MOLECOLA ELETTRODINAMICA DI AMPÈRE
In verità la prima spiegazione che Ampère dà della costituzione elettrica dei magneti, e che abbiamo appena visto, sarà rivista criticamente un paio di mesi dopo dallo stesso Ampère. Nella seduta dell’Académie del 15 gennaio 1821 Ampère lesse una memoria in cui compare per la prima volta, a fianco delle correnti macroscopiche che si muovono perpendicolarmente su linee chiuse intorno all’asse del magnete, l’ipotesi delle correnti particellari. Ecco quello che Ampère testualmente sostenne:
… Si tratta di sapere se le curve chiuse secondo le quali hanno luogo le correnti elettriche che forniscono all’acciaio magnetizzato le proprietà che lo caratterizzano, sono situate concentricamente intorno alla linea che unisce i due poli del magnete, o se queste correnti sono ripartite in tutta la sua massa intorno a ciascuna delle sue particelle, sempre nei piani perpendicolari a questa linea… .
C’era dunque da decidere quale di queste due ipotesi fosse quella esatta. Lo stesso Ampère disse che per fare ciò occorreva attendere finché dei nuovi calcoli e delle nuove esperienze abbiano fornito tutti i dati necessari alla sua soluzione.
A questo punto intervenne Agustin Fresnel (1788-1827) con due lettere private ad Ampère per suggerire la soluzione al problema. Fresnel nella prima lettera confronta, su base sperimentale, le due ipotesi di correnti intorno all’asse del magnete e di correnti intorno a ciascuna molecola ed arriva alla conclusione che è più verosimile quest’ultima ipotesi. Nella seconda lettera precisa ulteriormente questo concetto sostenendo:
… è facile vedere che, supponendo le correnti di uguale intensità intorno a tutte le particelle che si trovano lungo una barra magnetizzata, l’azione dovrà emanare solo dalla superficie che delimita la barra a ciascuna delle sue estremità, perché le azioni laterali di tutte le particelle costituenti la barra si neutralizzeranno dappertutto tranne che nei lati esterni delle particelle che si trovano alla estremità… .
Riporto, in figura, una sezione di un magnete cilindrico inteso costituito da molecole di Ampère:

L’ipotesi del magnetismo di Ampère

Disegno originale di Ampère
E’ da notare che Ampère sviluppò anche una teoria sul magnetismo terrestre basata sul fatto che dovevano esservi delle correnti circolanti da Est ad Ovest sulla Terra.
Da questo punto in poi Ampère userà sempre l’ipotesi di molecola circondata da una corrente elettrica. Questa molecola elettrodinamica di Ampère è d’importanza fondamentale: è la prima volta che si passa dalla concezione di correnti infinitesime, senza realtà fisica, che servono solo per ricavare relazioni matematiche, a correnti reali, anche se ipotetiche, che circondano le molecole costituenti il magnete. Questa concezione riduzionista di Ampère (derivare le proprietà magnetiche unicamente da correnti elettriche in piani perpendicolari al loro asse) è in linea con i tempi e risulterà di estrema importanza per gli sviluppi futuri delle teorie sulla costituzione degli atomi e dei magneti.
A margine della discussione dei fondamenti della scienza elettromagnetica vi erano altre questioni che si ponevano a seguito della scoperta della pila e dell’esperienza di Oersted.
La prima questione riguarda questa nuova grandezza che la pila originava, il passaggio con continuità del fluido elettrico o di quel che si vuole attraverso dei conduttore e, di conseguenza, la necessità di trovare qualcosa connesso a tale passaggio da misurare ed il relativo strumento di misura. A quest’ultima esigenza veniva incontro in modo indiretto l’esperienza di Oersted. Conosciuta l’esperienza furono Ampère e Laplace che si accorsero di un effetto notevole che si ricavava da essa: se un filo percorso dal fluido elettrico passa sopra e poi sotto l’ago, si ha un effetto somma della corrente nel senso che si moltiplica la sua azione sull’ago. Tale eventualità fa si che anche debolissimi fluidi elettrici transitanti in un filo possono essere rilevati dallo spostamento di un ago magnetico. Si tratta delle scoperta del principio che porterà alla costruzione dei primi galvanometri (misuratori di deboli correnti) e dei primi, come successivamente furono chiamati, amperometri (misuratori di correnti qualunque). Osservo tra parentesi che al fisico francese sono dovuti molti neologismi elettrici tra cui: galvanometro, elettrostatica, elettrodinamica, solenoide, … In particolare, anche il termine corrente elettrica è dovuto a lui. Quando infatti presentò la sua legge sulle azioni elettrodinamiche, prima si espresse in termini di attrazioni e repulsioni voltaiche e successivamente in termini di attrazioni e repulsioni tra correnti elettriche.
Fu il fisico tedesco Johann S. Schweigger (1779-1857) che in quello stesso anno realizzò uno strumento che moltiplicava ancora di più gli effetti di debolissimi
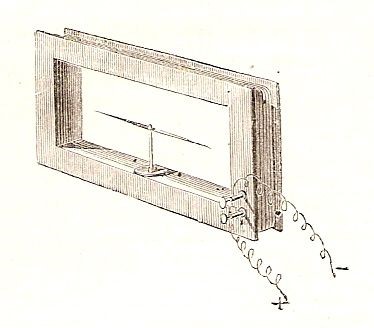
Moltiplicatore di Schweigger
flussi di fluido elettrico facendo passare il filo più volte intorno all’ago mediante il suo arrotolamento su un telaietto rettangolare. L’apparato fu ulteriormente migliorato l’anno successivo (Exposé des nouvelles découvertes sur l’électricité et le magnétisme…, 1822) dallo stesso Ampère che riuscì a togliere gli effetti di
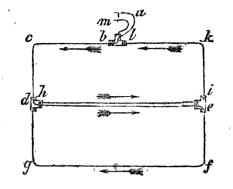
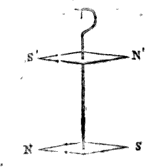
Il sistema astatico ideato da Ampère. E’ la sovrapposizione dei due apparecchi mostrati su: il primo elettrico con correnti circolanti in versi opposti ed il secondo magnetico con due aghi sistemati con polarità opposte.
orientamento dell’ago sotto il campo magnetico terrestre con il sistema astatico (due aghi magnetici collegati rigidamente e disposti con le polarità invertite). Ma il migliore strumento dell’epoca (1825) fu realizzato dal modenese Leopoldo Nobili (1784-1835) che ebbe l’idea di sospendere il dispositivo astatico ad un filo sottile
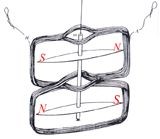
Sistema astatico utilizzato da Nobili
(anziché mantenerlo poggiato su una punta), aggiunse una campana di vetro per proteggere l’apparato da eventuale aria e sistemò al di sotto dell’ago una scala graduata.
FRANÇOIS ARAGO
Ho raccontato i lavori più importanti di Ampère evitando di inserire gli altri contributi che si ebbero subito dopo il lavoro di Oersted per evitare di frazionare troppo il discorso. E’ ora il caso di riprendere tali contributi, ciascuno dei quali aggiunse elementi spesso di notevole importanza per gli sviluppi successivi dell’elettromagnetismo(11).
Una tra le prime analisi dettagliate dell’esperienza di Oersted, subito dopo la comunicazione all’Académie di Arago, fu fatta, come già accennato, da Jean-Baptiste Biot e da Felix Savart che, in una sessione dell’Académie del 30 ottobre del 1820, riuscirono a fornire una determinazione molto accurata della legge di forza tra corrente ed ago magnetico(7). I due fisici misurarono con un cronometro di precisione le oscillazioni di fili magnetizzati in prossimità di un filo percorso da corrente ed in diverse condizioni. E trovarono una relazione che esprime precisamente l’azione che si esercita su un elemento infinitesimo [une molécule] di qualsivoglia polo magnetico, sistemato a diverse distanze da sottili ed indefiniti fili cilindrici, magnetizzati mediante la corrente di una pila. Il brevissimo resoconto di tale esperienza (una paginetta e mezza) dice quanto segue: Dal punto del polo dove è situato l’elemento infinitesimo, tracciate una perpendicolare all’asse del filo; la forza che agisce sull’elemento infinitesimo è perpendicolare a questa linea ed all’asse del filo. La sua intensità è il reciproco della distanza. Di seguito vi sono altre considerazioni che spiegano il perché l’ago magnetico ruoti sotto l’azione della corrente. Traducendo ciò in linguaggio moderno si può dire che la forza magnetica dovuta ad un elemento ds di un circuito, in cui fluisce una corrente i, ad un punto che dista r da ds, è data da
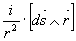
E’ da notare che, in quanto detto, vi è il riconoscimento che un campo magnetico [questo termine è ancora inappropriato e sarà opportuno solo dopo i lavori di Faraday] può essere prodotto allo stesso modo, sia da una corrente elettrica che da un magnete. Su quest’ultimo aspetto lavorò Arago pubblicando una memoria(12) in quegli stessi frenetici giorni. Egli iniziò a notare che un filo conduttore rame in cui passa corrente prodotta da una pila attira della limatura di ferro come un vero magnete. Sospendendo il flusso della corrente, la limatura cadeva a terra. Se la limatura era di rame non veniva attratta dal filo di rame percorso da corrente. Inoltre l’azione avveniva a distanza, era tanto maggiore quanto maggiore era la corrente fornita dalla pila e, se agiva su ferro dolce, essa cessava al cessare della corrente; se invece l’azione avveniva su acciaio si otteneva una magnetizzazione permanente. Arago aveva discusso di questi fenomeni con Ampère che nel frattempo aveva scoperto le azioni ponderomotrici. Questo scambio di informazioni permise ad Arago di servirsi non più di fili rettilinei ma di solenoidi per magnetizzare alcune sostanze. Con i dispositivi di figura seguente egli
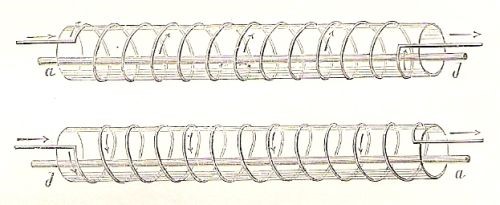
Metodo di Arago per magnetizzare sbarrette di acciaio
magnetizzò varie barrette di acciaio inserendole dentro dei solenoidi percorsi da corrente. Nel seguito della memoria Arago raccontava i molti arrangiamenti sperimentali che realizzò per stabilire dove si situavano i poli dei magneti così ottenuti. Le ultime righe del lavoro erano relative a tentare la spiegazione delle aurore boreali mediante le cose che aveva precedentemente trovato.
Quanto or ora raccontato è uno dei contributi di Arago alla scienza e neppure dei più importanti. Il nostro è famoso soprattutto per i suoi contributi alla misura del meridiano terrestre.
LA MISURA E L’AVVENTURA DI ARAGO
Arago nacque nel 1786 nel sud-ovest della Francia ed ebbe una vita piuttosto movimentata e discussa (qualcuno dice che i suoi meriti discendono da importanti conoscenze che aveva). Dopo aver fatto gli studi secondari al Liceo di Perpignan, nel 1803 entrò all’École Polytecnique di Parigi. Terminata i suoi studi superiori, nel 1805, con il sostegno di Laplace, entrò come bibliotecario all’Osservatorio di Parigi. Appena un anno dopo fu associato a Biot per una spedizione in Spagna che doveva misurare l’arco di meridiano passante per Parigi, operazione indispensabile per definire il sistema metrico decimale su cui era impegnato Napoleone.
La misura del meridiano terrestre era già stata tentata e realizzata varie volte a partire dal 1670 per valutare il diametro della Terra. A questo fine, negli anni, si impegnarono personalità di grande rilievo tra i quali Cassini e Maupetuis, eseguendo misure all’equatore, al polo ed addirittura nell’emisfero australe. Gli strumenti disponibili erano però poco affidabili e le misure lasciavano a desiderare fino ai lavori(13) del 1778 del fisico, matematico e ufficiale della marina francese Jean-CharlesdeBorda (1733-1799) che, impegnato in varie misurazioni sull’Atlantico (localizzazione delle Canarie e misura dell’arco di Meridiano), utilizzò due strumenti, il cerchio ripetitore ed il cerchio riflettente (particolari tipi di sestante), con i quali le misure si fecero più semplici (il cerchio ripetitore era stato

Il cerchio di Borda
realizzato dal suo assistente Etienne Lenoir che lavorò anche ad apportare perfezionamenti al cerchio riflettente, uno strumento realizzato dal tedesco Tobia Mayer nel 1752. Da notare che questo Lenoir, per i suoi meriti di costruttore di strumenti, fu subito assunto alla sezione del metro della Commission des Poids et Mesures, commissione in cui nel 1792 sedevano Lavoisier, Laplace, Condorcet y Legendre).
Con questi strumenti, Delambre e Mechain realizzarono la misura del meridiano terrestre da Dunkerque (estremo nord-est della Francia ai confini con il Belgio) a Barcellona. Il compito che fu invece assegnato a Biot nel 1806 era quello di proseguire la misura estendendo l’arco da Barcellona alle Isole Baleari (all’impresa dette la sua collaborazione il governo spagnolo con la messa a disposizione di una nave ed il governo britannico con i salvacondotti necessari per le Baleari, all’epoca dominio britannico). Nel 1807 Arago (aveva 21 anni) si unì ad
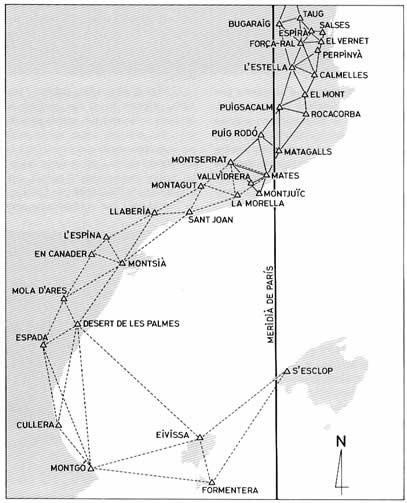
I triangoli scelti dai misuratori del meridiano terrestre. Individuo alcuni luoghi perché li si possano individuare da parte di chi conosce la Catalogna. In alto a destra vi è Perpignan (Perpinyà, che è l’ultima città francese al confine con la regione catalana di Spagna). Scendendo nella zona di terra (grigia) fino ad incrociare il meridiano (Meridià de París) si trova Montjuich (Montjuïc) che è l’altura che si trova sul porto di Barcellona. Le ultime località di terra, in basso a sinistra, si trovano sulla costa valenciana. Una delle isole è Ibiza (Eivissa), l’altra, dove è indicata la località di S’Esclop, è Mallorca.
Arago. Le misure vennero fatta mediante triangolazioni e continuando quelle iniziate dalla spedizione precedente. Nel mese di gennaio 2008 Biot tornò a Parigi con i dati di 11 triangoli (16 considerando anche quelli della precedente spedizione) per sviluppare i conti. Restava la triangolazione sulle isole che fu affidata ad Arago ed allo spagnolo Rodriguez. Arago nel maggio 1808 si spostò a S’Esclop, un’altura vicina al monte Galatzó, il più occidentale di Mallorca.

Il resto delle triangolazioni da Dunkerque a Barcellona
Ma a questo punto subentrarono tanti di quei problemi che meritano almeno un cenno. Durante le misure, gli scienziati si sistemavano sui rilievi più alti che riuscivano a trovare e si comunicavano, di notte, con segnali luminosi. Quando, sul finire di maggio 1808, l’ignaro Arago si trovava a S’Esclop a Mallorca scambiando segnali con lo spagnolo Rodriguez che si trovava sull’altura di Campvey ad Ibiza, la Spagna fu invasa da Napoleone. Arrivata la notizia nell’isola dell’insurrezione popolare contro i francesi nella penisola, anche a Mallorca la popolazione si sollevò contro i francesi presenti nell’isola. Qualcuno ricordò che sul monte vi era un francese che scambiava strani segnali subito intesi come operazioni di spionaggio. Un drappello spagnolo armato si diresse verso il monte per catturare la spia dell’imperatore francese. Il comandante della piccola nave che era stata messa a disposizione della Spagna per la spedizione si rese conto di cosa accadeva e riuscì a raggiungere prima degli altri Arago per portarlo in salvo vestito da contadino dell’isola e con la gran fortuna di parlare correttamente il mallorquino Non riuscì però ad abbandonare l’isola e, per salvarsi, chiese al comandante della nave di farlo rinchiudere nel castello medievale di Bellver. L’episodio è raccontato con ironia da Arago: Spesso si sono visti prigionieri scappare dalle prigioni per salvarsi. Forse io sono il primo che ha dovuto fare le cose alla rovescia.
Arago passò un mese nel castello dove lesse dai giornali portati da Valencia che era stato messo a morte. Poi Rodriguez riuscì ad ottenere che fosse scarcerato ma senza impegno di protezione. Con una barca da pesca si allontanò da Mallorca per raggiungere, qualche giorno dopo, Algeri. Il console francese lo imbarcò su una nave francese diretta a Marsiglia che però, vicino alle coste francesi, fu attaccata da una nave spagnola. Arago fu fatto prigioniero ed incarcerato a Rosas, sulla costa catalana. Furono le gestioni del Governatore (Dey) di Algeri a farlo rilasciare e rimetterlo su una nave algerina diretta a Marsiglia. Una tempesta nel Golfo del Leone stava spingendo la nave verso la Sardegna che era in guerra con l’Algeria. Sulla nave si decisero misure di emergenza: buttare gran parte del carico in mare per renderla governabile e dirigersi verso l’Africa dove arrivarono in una località (Béjaïa) distante tre giorni di marcia da Algeri. I berberi li assaltarono durante il viaggio e sequestrarono casse di strumenti che Arago si portava dietro religiosamente. Ad Algeri Arago chiese l’intervento del Dey, che nel frattempo era cambiato perché il precedente era morto qualche giorno prima per un ammutinamento, ma questi lo ridusse in schiavitù, usandolo come interprete. Fu il console francese ad insistere per la sua liberazione e quella degli strumenti. Riuscito nel suo scopo, di nuovo, fu imbarcato su una nave francese verso Marsiglia. Ma, questa volta, una nave inglese attaccò la francese ordinandole di dirigersi verso l’isola di Menorca nelle Baleari. Fu Arago che convinse il comandante a non ubbidire perché il vento risultava favorevole alla nave francese più piccola. La fuga ebbe successo e finalmente, Arago arrivò a Marsiglia con il suo prezioso bagaglio (1809). Quando si prende un metro in mano, si ricordi cosa è costata la sua determinazione.
Queste avventure, che paiono davvero incredibili, gli valsero la nomina a membro dell’Académie a soli 23 anni. Nello stesso anno il grande matematico Monge lo chiamò come suo supplente all’École polytecnique della quale diventerà professore aggiunto nel 1812. Resterà 20 anni ad insegnare all’École finché, nel 1830 non diventerà Segretario dell’Académie des Sciences. Da qui alla sua scomparsa nel 1853 ebbe molteplici onori e, partire dal 1830, dopo la scomparsa della moglie nel 1829, si dedicò alla vita politica.
LA MODERNIZZAZIONE DELL’OTTICA
Il Settecento è un secolo di esaltazione della scienza ed è il secolo in cui si fa di meno in campo scientifico. Tutti gli storici concordano sul fatto che la perfezione e l’apparente esaustività dei lavori di Newton avevano creato una sorta di soggezione che impediva l’avvicinamento alla ricerca e produzione scientifica. Ciò mostra quanto siano più utili lavori che abbiano dentro di sé importanti indeterminatezze logiche come, ad esempio, quelli di Maxwell.
Ricordo in breve che le teorie della luce che si confrontavano erano due, quella di Newton e quella di Huygens (per seguire una discussione molto più ampia si può leggere qui). Riporto, per comodità del lettore, una breve traccia di quanto ho già trattato altrove. La concezione di Newton è più articolata ed egli, anche se è universalmente noto come padre della teoria corpuscolare della luce, in realtà non prende una posizione precisa ma pone la questione in forma problematica. In certi passaggi sembra evidente una sua adesione alla teoria corpuscolare in assenza di etere; in altre parti della sua opera (Una nuova teoria sulla luce e sui colori – 1672) pare orientato verso la teoria ondulatoria sostenuta dall’etere («Le vibrazioni più ampie dell’etere danno una sensazione di colore rosso mentre quelle minime e più corte danno il violetto cupo; le intermedie colori intermedi»); in altri passaggi poi, come nell’Optiks (Libro II, parte III, proposizione XII, 1704), sembra invece propendere per un’ipotesi che si direbbe un compromesso tra una teoria ondulatoria ed una teoria corpuscolare, particelle precedute da onde, le quali in certo qual modo, predeterminano il comportamento
futuro delle particelle. Più oltre, il tentativo di spiegazione dei fenomeni di diffrazione unito al fatto che, secondo Newton, è impensabile una teoria che voglia la luce fatta di onde (“di pressioni”) perché le onde (“le pressioni”) “non possono propagarsi in un fluido in linea retta” a causa del fatto che hanno la tendenza a sparpagliarsi dappertutto, porta Newton alla formulazione (dubitativa) della teoria corpuscolare che si trova nella Questione 29 dell’Optiks.
Allo stesso modo del suono, dice invece Huygens riguardo alla sua teoria ondulatoria, la luce deve essere un fenomeno vibratorio e cosi come l’ aria sostiene il suono, altrettanto fa l’etere con la luce
“Ogni punto di un corpo luminoso, come il Sole, una candela o un carbone ardente, emette onde il cui centro è proprio quel punto … ; i cerchi concentricidescritti intorno ad ognuno di questi punti rappresentano le onde che si generano da essi … Quello che a prima vista può sembrare molto strano e addirittura incredibile è che le onde prodotte mediante movimenti e corpuscoli cosi piccoli possano estendersi a distanze tanto grandi, come, per esempio, dal Sole o dalle stelle fino a noi … Cessiamo però di meravigliarci se teniamo conto che ad una grande distanza dal corpo luminoso una infinità di onde, comunque originate da differenti punti di questo corpo, si uniscono in modo da formare macroscopicamente una sola onda che, conseguentemente, deve avere abbastanza forza, per farsi sentire.“
Possiamo riconoscere in queste poche righe la formulazione moderna della teoria ondulatoria fino al principio di Huygens o dell’inviluppo delle onde elementari.
Quando Huygens passava a dare una spiegazione dei fenomeni che oggi si spiegano con la polarizzazione egli, molto semplicemente, affermava che non gli era stato possibile trovare nulla che lo soddisfacesse. Riguardo poi alla natura di queste onde ed al loro modo di propagazione, Huygens diceva:
«Nella propagazione di queste onde bisogna considerare ancora che ogni particella di materia da cui un’onda si diparte, deve comunicare il suo movimento non solo alla particella vicina …, ma lo trasmette anche a tutte quelle altre che la toccano e si oppongono al suo moto».
E questa è una chiara enunciazione di quella che sarà la più grande difficoltà dell’ottica ondulatoria fino a Maxwell: il fatto che le onde luminose risultavano onde di pressione e quindi longitudinali. L’ammissione, inevitabile, di onde longitudinali e non trasversali impediva di pensare a qualsiasi fenomeno di polarizzazione (e quindi questa difficoltà era alla base di quanto Huygens confessava di non saper spiegare). Questo punto era ben presente a Newton che nell’Optiks lo cita e ne tenta una spiegazione ammettendo che i raggi di luce abbiano dei «lati» ciascuno dei quali dotato di particolari proprietà. Se infatti si va ad interpretare un fenomeno di polarizzazione mediante onde longitudinali, non se ne cava nulla poiché “queste onde sono uguali da tutte le parti”. E’ necessario dunque ammettere che ci sia una “differenza … nella posizione dei lati della lucerispetto ai piani di rifrazione perpendicolare.” Come già accennato solo la natura trasversale delle onde elettromagnetiche avrebbe potuto rendere conto, fino in fondo, dei fenomeni di polarizzazione.
C’è un altro aspetto che differenzia radicalmente la teoria ondulatoria da quella corpuscolare e riguarda la spiegazione del fenomeno di rifrazione (nel passaggio, ad esempio, da un mezzo meno ad uno più denso): nella teoria ondulatoria occorre ammettere che la velocità della luce sia minore nei mezzi più densi. Anche questo quindi diventava un elemento cruciale per decidere sulla maggiore o minore falsicabilità di una teoria. Se si fosse riusciti a determinare la velocità della luce in mezzi di diversa densità si sarebbe stati in grado di decidere quale teoria fosse più vera.
In linea con tutti gli altri campi della ricerca fisica, in Francia, i newtoniani decidono che Newton era un corpuscolarista e pertanto è la teoria corpuscolare della luce che trionfa (anche se coloro che portarono avanti queste idee abbandonarono l’altro punto che qualificava la teoria corpuscolare di Newton: il fatto cioè che il moto dei corpuscoli costituenti la luce originasse vibrazioni di un ipotetico etere). Questa scelta ha anche una giustificazione pratica di primo piano ed è che la teoria corpuscolare spiegava, più cose di quella ondulatoria; in particolare era molto più immediato con la prima teoria intendere la propagazione rettilinea della luce che, con la seconda, risultava piuttosto confusa (e non soddisfaceva neppure Huygens).
Proprio agli inizi dell’Ottocento un giovane medico britannico scoprì un fenomeno incredibile; luce sommata a luce, in alcune circostanze, origina buio! E’ il fenomeno dell’interferenza che fu scoperto nel 1802 da Thomas Young (1773-1829). Egli scriveva che il modo più semplice di provocare interferenza è
“quando un raggio di luce omogenea cade sopra uno schermo su cui sono stati praticati due piccoli fori o fenditure, che si possono considerare come centri di divergenza, dai quali la luce è diffratta in tutte le direzioni. In questo caso, quando i due raggi, nuovamente formatisi, vanno ad essere intercettati su una superficie interposta lungo il loro cammino, la loro luce risulterà suddivisa da bande scure in porzioni approssimativamente uguali.“
Anche Young si serviva di modelli meccanici e quello a cui egli si rifaceva per dar ragione di quanto avviene nell’ipotesi ondulatoria, è quello delle onde di acqua in uno stagno. Se due serie uguali di onde, provocate sulla superficie dell’acqua in punti a distanza opportuna, si incontrano, accadrà, egli osservava, che andranno a combinarsi in qualche modo. In ogni punto della superficie dell’acqua lo stato vibratorio risultante dipenderà dal modo in cui vanno a sommarsi o a sottrarsi gli effetti delle onde sovrapposte. E così, se le onde andranno a sommarsi, sovrapponendosi in concordanza di fase esse origineranno un’onda più grande delle due componenti prese separatamente; al contrario, se esse andranno ad incontrarsi in opposizione di fase, si distruggeranno l’un l’altra in modo da originare un’onda nulla (acqua immobile). Conseguentemente, il principio d’interferenza per la luce era così enunciato:
“Quando due parti di una stessa luce raggiungono l’occhio seguendo due diversi percorsi di direzioni molto vicine, l’intensità è massima quando la differenza dei cammini percorsi è un multiplo di una certa lunghezza; essa è minima per lo stato intermedio.”
A questo punto Young passava, a calcolarsi la lunghezza d’onda dei vari colori costituenti la luce a spiegare con la teoria ondulatoria i diversi fenomeni ottici conosciuti trovando grande difficoltà a rendere conto della propagazione rettilinea della luce: ma la difficoltà insormontabile restava sempre quella della spiegazione tramite la teoria ondulatoria ed usando di onde longitudinali (che Young, in analogia con il suono, riteneva essere caratteristiche della luce) dei fenomeni che oggi chiamiamo di polarizzazione.
La storia prosegue in Egitto. Nella spedizione napoleonica vi era Monge che non poteva resistere lontano ai suoi studi di geometria. In quel luogo fu sollecitato ad occuparsi di miraggi. Il 28 agosto 1798 lesse all’Institut d’Égypte una sua memoria sul miraggio(14), nella quale, per la prima volta, veniva presentata una spiegazione scientifica di quel fenomeno ottico che creava, nel deserto, visioni straordinarie. Questi studi di Monge influirono molto su Malus, un brillante studente dell’École Polytechnique che era venuto in Egitto al suo seguito.
E, nel 1808, Malus dette uno dei suoi contributi. In quest’anno Malus (1775-1812), che aveva appena pubblicato (1807) la memoria Traitè d’optique analytique e la Sur la mesure du pouvoir réfringent des corps opaques(15), partecipò ad un concorso bandito dall’Institut de France(16) che chiedeva una spiegazione teorica e sperimentale della doppia rifrazione. La memoria(17) che Malus presentò al concorso conteneva la scoperta di un nuovo fenomeno ottico

Doppia rifrazione attraverso un cristallo di calcite
che si rivelerà di enorme importanza, la polarizzazione della luce per riflessione (sciveva Malus: Se si fa cadere un fascio di luce sulla superficie di acqua stagnante, sotto un angolo di 52° 54’ con la verticale, la luce riflessa ha tutti i caratteri di uno dei fasci prodotti dalla doppia rifrazione da parte di un cristallo). Anche il termine polarizzazione è a lui dovuto e discende dal suo modo di considerare i corpuscoli di luce che egli supponeva costituiti da due polarità incandescenti che si sarebbero tutti orientati allo stesso modo quando avveniva la rifrazione in cristalli birifrangenti o quando si avevano riflessioni con determinati angoli. Malus riuscì a mettere in evidenza l’esistenza di tale fenomeno attraverso fenomeni di riflessione: un raggio di luce riflesso si comporta come uno dei raggi birifratti dallo spato d’Islanda e cioè non subisce più la doppia rifrazione se fatto passare di nuovo attraverso un cristallo dello stesso tipo. La spiegazione che Malus dava del fenomeno è riconducibile a quella newtoniana dei lati delle particelle, infatti egli pensava che i corpuscoli luminosi fossero asimmetrici e si orientassero sia durante la riflessione, sia durante una birifrazione, in modo da non potersi più orientare per successive riflessioni o birifrazioni. Newton si ma con qualche dubbio perché così scriveva Malus: adotto dunque l’opinione di Newton, non come verità indiscutibile, ma come un mezzo per fissare le idee e per interpretare le operazioni dell’analisi. È una semplice ipotesi , che d’altra parte non ha alcuna influenza sui risultati del calcolo. La commissione giudicatrice, composta da Laplace, Haüy, Chaptal, Berthollet, lo nominò vincitore del premio per la teoria della doppia rifrazione sviluppata e pubblicata nel 1810 con il titolo Théorie de la double réfraction de la lumière dans les substances cristallisés(18). E’ molto importante notare che la scoperta della polarizzazione si creerà un argomento importante per dirimere una controversia sulla natura delle onde luminose e sonore che si propagano nei fluidi poiché, mentre le prime sono polarizzabili, le seconde no.
Naturalmente la teoria corpuscolare era sostenuta da gran parte della scuola dei fisici-matematici francesi tra cui Biot e Poisson (che tenteranno in tutti i modi, senza però riuscirvi, di ricondurre i fenomeni di interferenza alla teoria corpuscolare), Laplace e, per un certo tempo, Arago. E fu proprio quest’ultimo che, in un ambiente generalmente ostile, dette un importante sostegno al fisico che doveva dare nuovo impulso alla teoria ondulatoria fino a portarla al suo trionfo: Augustin Fresnel.
Come dice Whittaker, ancora nella prima metà degli anni Venti dell’Ottocento, la teoria ondulatoria della luce era gravata da molte difficoltà. La diffrazione era spiegata in modo non soddisfacente; non era disponibile alcuna spiegazione per la polarizzazione; la costruzione realizzata da Huygens richiedeva due diversi mezzi per il trasporto della luce al fine di spiegare il comportamento dei corpi doppiamente rifrangenti (come quelli scoperti da Brewster nel 1814); non si comprendeva perché si ottiene una polarizzazione completa mediante riflessione quando i raggi riflesso e rifratto sono ad angolo retto tra loro (Brewster 1815).
Un altro importante sostegno alla teoria corpuscolare venne della teoria di Laplace della doppia rifrazione (1809)(19). Egli, facendo arrabbiare Malus che in qualche modo si era sentito scavalcato e copiato, era riuscito a conciliare, mediante l’analisi ed utilizzando il principio di minima azione, la teoria di Huygens con quella di Newton ed aveva fatto addirittura pensare che era arrivato il momento della accettazione definitiva della teoria corpuscolare. E proprio a tal fine, nel marzo 1817 fu proposto il tema Diffrazione per il concorso dell’Acadèmie del 1818. Al concorso partecipò il giovane e brillantissimo ex allievo dell’École, poi diventato ingegnere di strade e ponti, Augustin Fresnel (1788-1827), che, con il sostegno di Arago, presentò una ponderosa memoria (di ben 140 pagine) sul fenomeno(20). Tale memoria era stata una rielaborazione approfondita di una precedente memoria presentata all’Académie nel 1816. La giuria era composta da Laplace, Biot, Poisson, Arago (nominato relatore) e Gay-Lussac e tutti (meno Poisson che aspettava qualche esperienza decisiva) furono d’accordo nel concedere il premio del concorso a Fresnel. Questi aveva avuto la grande idea di accordare in modo convincente i vari e proficui concetti che i vari autori del passato avevano sviluppato: l’idea delle onde elementari, del loro inviluppo (Huygens), dell’interferenza (Young). Come dice Ronchi, “egli fece la considerazione fondamentale che un inviluppo di onde non è un inviluppo geometrico, ma l’effetto risultante in un punto qualunque dell’inviluppo stesso è la somma algebrica degli impulsi che vi arrecano le singole onde elementari; impulsi che, ben lungi dall’essere tutti uguali o tutti concordi, possono anche essere contrastanti e dare un effetto globale nullo. Bisognava eseguire questa somma algebrica, ossia l’integrazione degli impulsi elementari che in determinate circostanze arrivano in un dato punto. Fresnel cominciò dal caso di un’onda piana: per calcolarne l’effetto sopra un punto P antistante, immobilizzò il fronte dell’onda in una posizione e lo suddivise in tante «zone» circolari concentriche, aventi per centro il piede della perpendicolare abbassata dal punto P sul fronte stesso. In assenza di diaframmi o di ostacoli di qualsiasi genere, il fenomeno presenta una simmetria di rotazione attorno a questa retta; perciò deve essere possibile tagliare sul fronte d’onda tante zone circolari concentriche, i punti di ciascuna delle quali inviano nel punto P delle vibrazioni in opposizione di fase rispetto a quelle inviate dalle zone contigue. Il calcolo globale, anche se eseguito in un modo non troppo rigoroso, portò Fresuel a concludere che l’effetto risultante delle vibrazioni inviate da tutto il fronte nel punto P era uguale a quello di una piccola superficie del fronte stesso attorno al piede della normale suddetta; perchè tutto il resto preso globalmente dava un totale nullo.
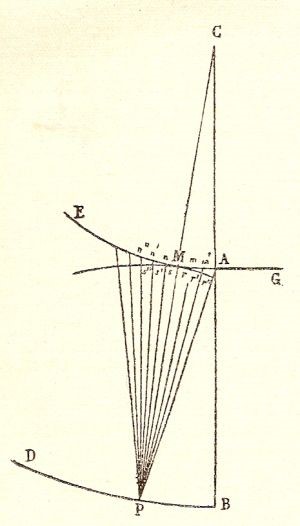
Figura di Fresnel con la quale egli calcola il suo integrale che gli serve per la spiegazione le frange di diffrazione all’orlo dell’ombra di un ostacolo.
La secolare accusa per cui col meccanismo ondulatorio non era possibile la propagazione rettilinea veniva a cadere definitivamente dopo questa dimostrazione. Si svelava ora l’errore logico che era stato ripetuto per tante volte e per tanti anni: è vero che le onde debbono girare gli ostacoli «come fa il suono»; ma il fenomeno non deve essere apprezzato così sommariamente e intuitivamente, estendendo a tutti i casi ciò che appare evidente in qualche esperienza; lo studio deve essere quantitativo, perché gli effetti sono funzioni della lunghezza d’onda.
La luce che aveva una lunghezza d’onda piccolissima doveva dare effetti visibili di rotazione attorno agli ostacoli o di deviazione dal cammino rettilineo quando gli ostacoli erano piccolissimi, e doveva deviare di tratti molto piccoli: appunto come avveniva nelle esperienze di diffrazione. I calcoli di Fresnel corrispondevano all’esperienza con una precisione meravigliosa. Poisson, geometra rigorosissimo, obbiettò che secondo la teoria delle «zone» di Fresnel, doveva apparire la luce nel centro dell’ombra di un dischetto opaco, capace di coprire una determinata calotta del fronte d’onda. Egli giudicava assurda questa conclusione e quindi la teoria; ma l’esperienza eseguita da Arago confermò brillantemente la previsione. La cosiddetta propagazione rettilinea della luce e la diffrazione venivano così conciliate e assestate in tutti i loro particolari. Le idee di Huyghens, così completate, assurgevano al valore di teoria «vera»”.
Tutto quanto detto, sia il modo di propagazione delle onde, sia i vari fenomeni discussi, vide una completa formalizzazione con l’introduzione, come accennato degli integrali (integrali di Fresnel). Evidenziò un fatto importante e cioè che l’omogeneità e la coerenza delle onde sono ciò che permette la loro interferenza. Nella sua elaborazione furono trattati tutti gli aspetti dei problemi in gioco e ricavate le relazioni che esistono tra ampiezze e quindi intensità delle onde incidenti, riflesse e rifratte.
La obiezione di Poisson a Fresnel merita due parole. Letto il manoscritto egli non trovò errori importanti e quindi obiettava che la correttezza della spiegazione ondulatoria doveva essere estesa ad altri fenomeni come, ad esempio, alla macchia luminosa che si forma al centro dell’ombra di uno schermo circolare, fenomeno descritto da J.N. Delisle nei primi anni dell’Ottocento. Ed anche questo fenomeno venne facilmente spiegato con la teoria ondulatoria, come ogni altro fenomeno che via via veniva proposto a Fresnel.
Nel merito più dettagliato, la memoria di Fresnel era estremamente accurata anche nella sperimentazione proprio perché, non riuscendo a leggere le memorie originali di Grimaldi e Young perché non conosceva le lingue, doveva rifare tutto da capo. Fu Arago che lo aveva informato dell’esperienza di Young e da quella egli partì proponendosi di indagarlo meglio. Poteva sorgere il dubbio, infatti, che le frange d’interferenza osservate non fossero altro che fenomeni di diffrazione provocati dal passaggio della luce nei piccoli forellini. Egli trovò così un altro modo di produrre interferenza che non poteva far sorgere dubbi. Anziché usare i forellini di Young fece riflettere (già nella memoria del 1816) un raggio di luce, proveniente da una sorgente puntiforme, su due specchi consecutivi formanti tra loro un angolo prossimo a 180° nel modo indicato nelle figure (a) e (b) seguenti.
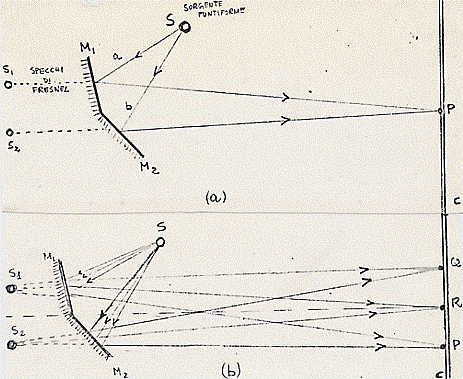
Riferendoci alla figura (a), un raggio (onda) luminoso a emesso dalla sorgente puntiforme S, si riflette sullo specchio M1 e si dirige verso il punto P dello schermo C. Analogamente esisterà un altro raggio (onda) b, proveniente da S che si dirigerà verso P. Poiché i cammini dei due raggi sono differenti, i due raggi, in generale, risulteranno sfasati tra loro. Nel caso in cui vi sia concordanza di fase tra le due onde, P sarà un punto in cui si avrà un massimo di illuminazione; nel caso in cui le due onde siano in opposizione di fase, in P vi sarà buio; nel caso di sfasature diverse vi sarà una variazione dell’ intensità dell’illuminazione dal buio al massimo di cui dicevamo. L’effetto complessivo sarà un fenomeno d’interferenza, analogo a quello che sarebbe generato da due sorgenti puntiformi S1 ed S2, che si osserverà sullo schermo C.
La figura (b) mostra invece più onde che vanno ad interferire in diverso modo sullo schermo C. A seconda del tipo di interferenza, e quindi di sfasatura, tra le onde interessate, i punti P, Q, R saranno bui o illuminati a varie intensità
Con questa esperienza Fresnel sgombrò contemporaneamente il campo sia dall’interpretazione erronea del fenomeno dovuta ai corpuscolaristi (le frange non hanno nulla a che vedere con l’interazione di tipo gravitazionale tra le pretese particelle di luce ed i bordi delle fenditure) sia da quella altrettanto erronea di Young (le frange non sono generate dall’interferenza delle onde dirette con quelle riflesse dai bordi delle fenditure). La chiave della corretta interpretazione di Fresnel fu proprio la ripresa del principio di Huygens: ogni punto di una superficie di un’onda può diventare fonte di onde secondarie. Ebbene, nel fenomeno d’interferenza creata con due forellini, ciascun forellino diventa sorgente di onde; sono le onde che provengono da un forellino che interferiscono con quelle che si dipartono dall’altro. Nella figura seguente vi è la ricostruzione della spiegazione

Figura tratta da A. De Marco – Fisica 2 – Poseidonia 1977.
mediante le onde dell’interferenza di Young (due forellini): le due fenditure O1 ed O2 del secondo diaframma B formano due sorgenti (principio di Huygens) che vanno ad illuminare lo schermo C. Nel tragitto tra B e C le onde provenienti dalle due sorgenti interferiscono tra loro. Nei punti M le onde arrivano in fase e si hanno massimi di illuminazione. Nei punti N si ha invece interferenza distruttiva (onde controfase) e si hanno punti di minima illuminazione.
Vale la pena spiegare meglio quanto detto. Intanto riporto i disegni della sezione di onde: (a) due onde in fase e la loro somma, (b) due onde sfasate e la loro somma, (c) onde in controfase e la loro somma.
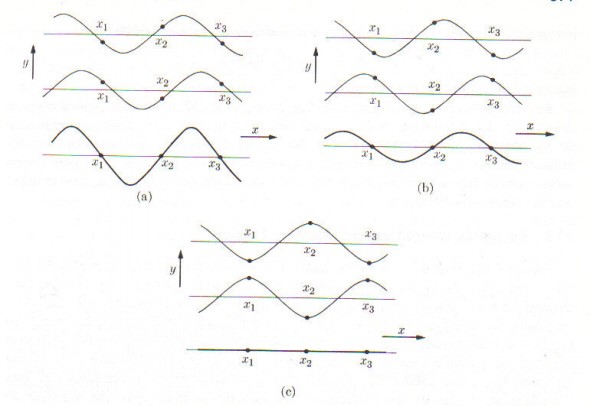
Si può osservare che la somma delle due onde in (a) fornisce un’onda con massimi e minimi somma delle onde che la originano (questa situazione corrisponde al massimo di illuminazione); in (c) si ha un’onda risultante nulla (buio); in (b) una situazione intermedia (penombra). Resta ora da vedere qual è il meccanismo analitico che, sullo schermo origina una situazione di luce o di buio. Per farlo serviamoci della figura seguente e riferiamoci a due figure indietro (spiegazione visiva mediante le onde dell’interferenza).
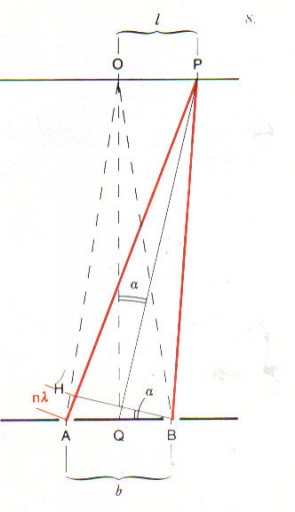
I due fori che avevamo prima (O ed O’) sono ora A e B. Il punto M che avevamo prima è ora O. Lo schermo C di prima è ora OP. Supponiamo di lavorare con luce monocromatica, con luce costituita da una sola lunghezza d’onda. I due raggi che da A e B arrivano in O percorrono un cammino di uguale lunghezza e quindi, essendo partiti in fase dato che fanno parte di una stessa onda (che ne origina due da A e B per il principio di Huygens), sono ancora in fase e vanno a sommarsi in O. Ciò origina in O una maggiore illuminazione. Le onde che invece arrivano in un punto qualsiasi P dello schermo avranno percorsi diversi, PA e PB la cui differenza sarà PA – PB. Ora vi sono due possibilità: o PA – PB è uguale ad un multiplo intero della lunghezza d’onda, cioè nl, con n = numero intero; o PA – PB è uguale ad un multiplo semintero della lunghezza d’onda (n + ½) l. Nel primo caso, l’onda che parte da A arriva in H in modo da riavere la stressa fase dell’onda che sta uscendo da B ed allora da questo punto in poi le due onde viaggiano in fase ed in P si avrà luce. Nel secondo caso, l’onda che parte da A arriva in H in modo da essere in controfase con l’onda che sta partendo da B ed allora da questo punto viaggeranno in controfase ed in P si avrà buio.
Ma fin qui le onde luminose pensate da Fresnel erano longitudinali. Egli, nella sua memoria del 1816, diceva: “in ogni punto dello spazio dove sta condensato, l’etere è compresso e tende ad espandersi in tutte le direzioni“, e queste non sono altro che onde longitudinali.
Ancora nel 1816 Fresnel ed Arago scoprirono che due raggi polarizzati sullo stesso piano interferiscono, mentre se sono polarizzati su piani tra loro perpendicolari non interferiscono più(21). Si introduceva il problema della polarizzazione in una situazione nuova. Il risultato di questa esperienza fu comunicato a Young dallo stesso Arago che nel 1816 si era recato a Londra insieme a Gay Lussac. Young rifletté molto su quanto aveva appreso e, in una lettera ad Arago del 1817, avanzò l’ipotesi che le onde luminose fossero onde di tipo trasversale(22). Arago ne informò Fresnel il quale fece sua l’ipotesi e cominciò a lavorarvi con gran lena. Tra il 1821(23) ed il 1823 Fresnel riuscì a dimostrare che, con questa ipotesi, era possibile spiegare tutti i fenomeni ottici conosciuti (a questo punto però Arago si dissociò da Fresnel e non volle firmare con lui una memoria sull’argomento perché, per sua stessa ammissione, non ebbe il coraggio di sostenere l’idea di onde trasversaliche era argomento troppo grosso da ingoiare per tutti i fisici dell’epoca). In particolare, nella memoria del 1821, Fresnel si rese conto di cosa implicavano le vibrazioni trasversali per la costituzione dell’etere ed iniziò a definirne un modello che doveva rispondere in modo elastico alle distorsioni provocate dalle vibrazioni trasversali. Fatta questa premessa egli discuteva di polarizzazione ipotizzando che la luce sia composta da un insieme di raggi polarizzati (mediante vibrazioni trasversali) in ogni direzione e che l’incidenza di essa su un cristallo non crea polarizzazione ma seleziona le onde del fascio incidente polarizzate in una data direzione. Egli non escludeva poi l’esistenza nell’etere anche di vibrazioni longitudinali (ulteriore complicazione per definire le proprietà elastiche dell’etere). La propagazione rettilinea, invece e come già accennato, che era stata sempre un grosso problema per la teoria ondulatoria, interpretata correttamente mediante i fenomeni d’interferenza (il movimento che un’onda sferica trasmette si distrugge in parte per interferenza), non rappresentava più un problema per questa teoria. Occorre accennare ad un’altra importante memoria che Fresnel presentò ancora all’Académie nel 1818(24), l’anno in cui Fresnel presentò la sua memoria sulla Diffrazione che gli fece vincere il premio. E’ d’interesse per gli sviluppi futuri sullo studio dell’etere. In essa Fresnel iniziò ad occuparsi di un problema estremamente avanzato come l’effetto del moto della Terra sulla luce discutendo di quel fenomeno che va sotto il nome di aberrazione. Parlerò di ciò nel prossimo paragrafo.
Di problema, semmai, ne nasceva un altro e fu lo stesso Fresnel a prospettarlo nel 1821. Ammesse le onde trasversali che così bene spiegavano tutti i fenomeni ottici, che caratteristiche avrebbe dovuto avere l’etere per permettere il loro passaggio ? Le onde longitudinali marciano bene in un fluido, ma per le onde trasversali occorre un solido e neppure un solido qualunque. Questo solido dovrebbe avere una rigidità teoricamente infinita (vista l’enorme velocità di propagazione della luce), quindi più elevata di quella dell’acciaio, e nel contempo deve essere più evanescente di ogni gas conosciuto per non offrire resistenza ai corpi celesti che da secoli vediamo muoversi nel cielo senza apprezzabili rallentamenti. Occorre a questo punto avvertire che ogni argomentazione sulle onde luminose veniva fatta, all’epoca, in analogia con quelle sonore (in cui le vibrazioni sono sempre parallele alla direzione di propagazione) e quindi non era stata ancora sviluppata una teoria della propagazione delle onde nei solidi elastici. Fresnel comunque non ebbe modo di seguire il corso degli eventi: nel 1827, a soli 39 anni, morì di tubercolosi. Prima di questo tragico evento, Fresnel fu nominato (1819) membro della commissione per i fari marini. Passò nel 1821 ad insegnare fisica e geometria all’École Polytechnique. Nel 1822 inventò le famose lenti che portano il suo nome e che permettono di aumentare notevolmente la luminosità di una sorgente (e quindi dei fari marittimi) senza aumentare l’ingombro e la massa (queste lenti le si possono trovare, oggi, nelle lavagne luminose in uso in convegni e conferenze ma anche nei fanali di posizione o indicatori di direzione degli automobili). Nello stesso anno, la sua spiegazione della birifrangenza gli fece ottenere l’ambito riconoscimento del corpuscolarista Laplace. Nel 1823 viene eletto membro dell’Académie del Sciences, all’unanimità.
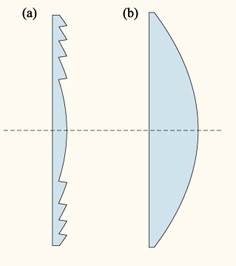
In (a) vi è la sezione di una lente di Fresnel (che oggi può essere costruita con un disco di plastica opportunamente inciso) a confronto con una lente ordinaria (b).
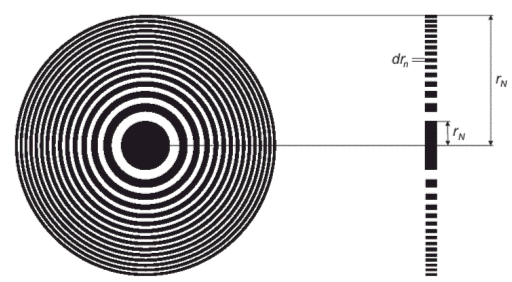
Altra immagine che mostra una lente di Fresnel di fronte ed in sezione.
I lavori di Fresnel aprirono la strada ad una gran mole di ricerche sia teoriche che sperimentali. In particolare l’analogia tra onde luminose ed onde elastiche, che scaturiva dalla teoria di Fresnel, apriva un vasto campo di ricerche sui fenomeni dell’elasticità.
Di tentativi di risoluzione di questi problemi ne furono fatti tantie dal corpo della loro elaborazione analitica, con la matematica sviluppata dalla scuola francese nel ‘700, con quella sviluppata dai Green e dagli Stokes in Gran Bretagna e con altra che via via veniva ideata allo scopo, scaturirono moltissimi teoremi che furono poi di grande utilità per gli sviluppi ulteriori della fisica (particolarmente Maxwell).
Altro campo di ricerche aperto dalla polemica onde o corpuscoli era quello relativo alla velocità della luce. Come abbiamo visto nel capitolo precedente, la spiegazione della rifrazione mediante la teoria corpuscolare prevede che la velocità della luce sia più grande nei mezzi più densi, esattamente il contrario di quanto previsto dalla teoria ondulatoria. C’è l’opportunità di un esperimento cruciale che possa decidere quale teoria descrive meglio i fatti sperimentali osservati.. La crucialità di questa eventuale esperienza era stata sostenuta nel 1838 da Arago che, nel 1810, aveva tentato un’esperienza che dirimesse la polemica tra teoria corpuscolare ed ondulatoria. Il suo progetto era di misurare la velocità della luce mediante uno specchio rotante. A tal fine si ingegnò alla realizzazione di tale strumento che fu pronto solo nel 1850, quando lo stesso Arago era diventato cieco. Con alcune modifiche la sua apparecchiatura fu utilizzata da Foucault e Fizeau. Fino a circa la metà dell”800 quindi le uniche misure della velocità della luce (che da ora indicherò direttamente con c) erano state eseguite su fenomeni astronomici (Röemer e Bradley), non si era ancora trovato il modo di misurare c sulla Terra: il suo elevato valore fa sì che la luce percorre tragitti lunghissimi in tempi brevissimi e tragitti di tale lunghezza non esistono in natura sulla Terra a meno di realizzarli con particolari artifici.
Il primo strumento in grado ai permettere misure di c sulla Terra, che appunto si serviva degli artifici suddetti, fu ideato dal fisico francese H. Fizeau nel 1849 su idea di Arago. L’esperienza di Fizeau permise la misura di c nell’aria ma fu impossibile realizzarla in un altro mezzo perché la distanza su cui Fizeau aveva operato in questa sua prima esperienza, era di circa 9.000 metri.
Chi riuscì ad effettuare la misura di c, non solo sulla Terra, ma nei limiti ristretti di una stanza di laboratorio, fu l’altro fisico francese, L. Foucault, nel 1850. L’essere riusciti a portare questa misura in laboratorio apriva la strada, immediatamente percorsa, alla misura di c in diversi mezzi ed in particolare nell’acqua.
EFFETTI DEL MOTO DELLA TERRA SULLA LUCE
Nel contesto della difesa della teoria corpuscolare, i fisici di formazione meccanicista si misero subito al lavoro nel tentativo, almeno, di dirimere la questione sperimentalmente. In questo contesto, tra il 1809 ed il 1810, Arago ideò e realizzò un’esperienza(25) i risultati della quale avrebbero dovuto, almeno nelle intenzioni, dare una risposta definitiva sulla natura corpuscolare od ondulatoria della luce. Si noti che una esperienza di questo tipo era stata proposta da Boscovich nel 1766. Boscovich proponeva di utilizzare il metodo di Bradley per la determinazione della velocità della luce semplicemente riempiendo il cannocchiale utilizzato da Bradley d’acqua al fine di fare un qualcosa di analogo a quanto farà poi Fizeau: determinare come il mezzo influisce su c. Ma proprio a seguito di questa, esperienza di Arago si arrivò a stabilire che il moto della Terra non ha alcuna influenza sul fenomeno della rifrazione della luce proveniente dalle stelle. A seguito di ciò Fresnel ne concluse l’impossibilità dell’esperienza proposta da Boscovich. L’esperienza fu poi tentata da Airy tra il 1871 ed il 1872 confermando le previsioni di Fresnel.
Era noto che la luce ha velocità diverse in mezzi diversi e questo fatto doveva essere ammesso dalle due teorie della luce per rendere conto del fenomeno della rifrazione. Ma mentre la teoria corpuscolare assegnava alla luce una maggiore velocità quando essa passava da un mezzo meno ad uno più denso, la teoria ondulatoria doveva prevedere un rallentamento della luce nel passaggio a mezzi più densi. Arago pensò quindi di utilizzare il fenomeno della, rifrazione per tentare di dirimere la controversia. La sua idea era di far esperienze di rifrazione “al contrario” e cioè, anziché cambiare i vari mezzi per studiare, a parità di velocità della luce incidente, le diverse rifrazioni in esse, si poteva mantenere sempre lo stesso mezzo e sfruttare la variazione ai velocità della luce, proveniente da una stella, che sulla Terra deve risultare, in diversi periodi dell’anno, a seguito del principio classico di relatività. Infatti, ammesso il principio di relatività ed il moto della Terra intorno al Sole, a sei mesi di distanza, quando la Terra ha percorso metà della sua orbita, la luce proveniente da una fissata stella comporrà diversamente la sua velocità con quella orbitale della Terra (vedi figura seguente). In un dato periodo dell’anno (punto A di figura) la luce proveniente

Si noti che, data l’enorme distanza della stella dalla Terra, il diametro dell’orbita terrestre intorno al Sole risulta del tutto trascurabile e quindi le due linee costituite dalle frecce tratteggiate possono essere considerate parallele
dalla stella cadrà sulla Terra che si muove, ad esempio, nella stessa, direzione e verso; sei mesi dopo (punto B di figura) la luce proveniente dalla stella cadrà sulla Terra che si muove nella stessa direzione ed in verso opposto rispetto ad essa. Detta allora v la velocità orbitale della Terra e c quella della luce proveniente dalla stella, secondo il principio di relatività (e rispetto all’etere fino ad ora supposto immobile;
– in A: la velocità risultante della luce dovrà essere c – v (tutto va come se la Terra fosse immobile e la sorgente di luce si allontanasse da essa con velocità v);
– in B: la velocità risultante della luce dovrà essere c + v (tutto va come se la Terra, fosse immobile e la sorgente di luce si avvicinasse ad essa con velocità v).
Ecco quindi come Arago pensò di modificare le esperienze di rifrazione: egli puntava il cannocchiale su una stella opportunamente situata nel cielo; l’immagine della stella , prodotta dal cannocchiale, era inviata su un sottile prisma nel quale avveniva il fenomeno della rifrazione; l’effetto del prisma, era quello di spostare leggermente fuori dall’asse questa immagine; a sei mesi di distanza si andava di nuovo ad osservare l’immagine nella previsione, appunto, che, essendo variato l’angolo di rifrazione a seguito della variazione della velocità della luce, essa si sarebbe trovata spostata. Ebbene, nel caso fosse valsa la teoria corpuscolare, lo spostamento dell’immagine dall’asse sarebbe dovuto diminuire; nel caso fosse valsa la teoria ondulatoria, lo spostamento dell’ immagine dall’asse sarebbe dovuto aumentare. Gli spostamenti dell’immagine dall’asse dovevano essere proporzionali a 2.v/c, dove 2v è la differenza tra la velocità della luce nelle due situazioni A e B, e c è la velocità della luce considerata rispetto all’etere supposto in quiete. Una dipendenza di questo tipo (proporzionale a v/c) è detta del primo ordine. Dall’esperienza di Arago doveva scaturire un effetto del primo ordine nel rapporto v/c, gli unici effetti che, all’epoca, potevano essere osservati. Infatti, nel passare dalla posizione A alla posizione B di figura, la velocità risultante della luce aumenta e:
– per la teoria corpuscolare, il passare ad una velocità più grande corrisponde ad avere un mezzo più denso con la conseguenza che l’angolo di rifrazione deve diminuire;
– per la teoria ondulatoria, il passare ad una velocità più grande corrisponde ad avere un mezzo meno denso con la conseguenza che l’angolo di rifrazione deve aumentare.
Fatta l’esperienza, Arago trovò che non c’era stato spostamento alcuno della immagine della stella. La luce cioè, viaggiando da una data stella, si comporta in tutti i casi di riflessione e rifrazione come se la stella fosse situata nel luogo in cui essa appare a seguito dell’aberrazione con la Terra come se fosse immobile cosicché la rifrazione su un prisma in moto corrisponde a quella in un prisma immobile. Come si usa dire, il risultato dell’esperienza fu negativo; esso dimostrò che il moto orbitale della Terra non influisce sulla rifrazione della luce proveniente dalle stelle.
Che conclusioni trarne ?
Arago, ottimo conoscitore della teoria corpuscolare, ne dedusse che per spiegare il fenomeno alla luce di questa teoria occorreva ammettere dei fatti che a lui sembravano non credibili e cioè che:
– i corpi luminosi emettono corpuscoli di tutte le velocità;
– solo i corpuscoli che hanno determinate velocità sono da noi visibili;
– solo questi ultimi producono negli occhi la sensazione di luce.
Tutto ciò non sembrò credibile ad Arago. E neanche fu in grado di sviluppare una approfondita indagine nell’ipotesi ondulatoria che, come abbiamo visto, nel 1810 era ancora tutta da costruire.
Negli anni immediatamente successivi Arago sviluppò dei rapporti sempre più stretti con Fresnel il quale, nel frattempo, aveva fornito la teoria ondulatoria di un impianto teorico molto solido. E nel 1818 Arago scrisse a Fresnel ponendogli il problema dei risultati della sua esperienza osservando che non potevano essere spiegati con la teoria emissionistica (corpuscolare). Forse che con la teoria ondulatoria, mediante qualche strano meccanismo di propagazione delle onde o mediante qualche proprietà dell’etere sarebbe stato possibile spiegare il fenomeno ?
Era questa in sostanza la domanda che Arago rivolgeva a Fresnel. La posta in gioco era alta: la rimessa in discussione della teoria ondulatoria che spiegava bene tutti i fatti sperimentali fino ad allora noti. La spiegazione di tutto poteva ritrovarsi nell’etere ? Potrebbe trattarsi di una qualche particolare interazione tra etere e corpi in movimento ? E su quest’ultima strada si mosse Fresnel nella sua risposta ad Arago quello stesso anno. Egli scriveva:
“Mi avete stimolato ad esaminare se il risultato di tali osservazioni possa essere riconciliato più facilmente con la teoria nella quale la luce è considerata in termini di vibrazioni di un fluido universale. E’ del tutto necessario trovare una, spiegazione all’interno di questa teoria …
Qualora si dovesse ammettere che la nostra Terra trasferisce il proprio movimento all’etere che lo circonda(26), sarebbe allora facile vedere il motivo per cui un medesimo prisma dovrebbe sempre rifrangere la luce nello stesso modo, quale che sia la direzione di provenienza della luce stessa. Ma sembra impossibile spiegare l’aberrazione delle stelle mediante questa ipotesi: io sono stato incapace, almeno sino ad ora, di capire con chiarezza questo fenomeno, se non supponendo che l’etere passi liberamente attraverso il globo terrestre, e che la velocità comunicata a questo fluido sottile sia solo una piccola parte della velocità della Terra,non maggiore, ad esempio, di una centesima parte.“(27)
Per risolvere il problema, quindi, Fresnel aggiunge una ipotesi (che poi svilupperà analiticamente), quella del trascinamento parziale dell’etere(28). Fino ad ora, nel discutere l’esperimento di Arago, avevamo supposto che il moto della Terra avvenisse in un immobile oceano di etere con la conseguenza che la Terra si trascinava dietro irrisorie quantità d’etere, per dirla con Einstein, “esattamente come una rete appesa ad un’imbarcazione trascina l’acqua“. E’ questa allora l’ipotesi che va cambiata ed in modo opportuno, così da rendere conto dei risultati sperimentali. A causa del moto della Terra nell’etere deve sorgere un qualche effetto che elimini le discordanze tra teoria ed esperimento.
Fresnel suppose allora che l’etere fosse trascinato dal moto della Terra quel tanto che bastasse a compensare l’effetto di composizione delle velocità della luce e della Terra. L’etere, che impregna tutti i corpi, è contenuto nella materia costituente la Terra (come una. spugna contiene l’acqua al suo interno); secondo Fresnel, nel suo moto la Terra trascina solo una parte dell’etere in essa contenuto: una parte di esso se ne va dalla parte posteriore della Terra in moto ed una pari quantità entra dalla parte anteriore (cosicché all’interno della Terra c’è sempre la stessa quantità di etere)(29). Ciascun corpo, quindi, che si trova sulla Terra, trascina una parte dell’etere in esso contenuto ed in particolare la lente del cannocchiale ed il prisma (dell’esperienza di Arago) trascinano una parte dell’etere in essi contenuto. E, come dicevano Einstein ed Infeld, “la velocità della luce nell’etere in riposo dovrebbe essere differente da quella dell’etere trascinato … precisamente come la velocità di un’onda sonora differisce secondo che l’aria e’ calma o che tira. vento“. Il problema era di stabilire quanto etere fosse trascinato. Fresnel, con considerazioni di carattere teorico, riuscì a stabilire che la quantità di etere trascinato dipendeva dall’indice di rifrazione n della sostanza in cui si propaga la luce(30). Egli riuscì anche a ricavare una formula che forniva la velocità della luce in un dato mezzo in funzione del trascinamento parziale dell’etere contenuto in esso. Nella formula questo trascinamento è espresso mediante un coefficiente α (coefficiente di trascinamento) che è funzione dell’indice di rifrazione n del mezzo in cui si propaga la luce:
α = 1 – 1/n2
La formula per la velocità della luce in un dato mezzo (w) era poi data da(31):
w = c/n ± Δv (1 – 1/n2 ),
dove v rappresenta la velocità di spostamento del mezzo rispetto all’etere immobile. Una considerazione che si può immediatamente fare è relativa alla formula ora data: il trascinamento è tanto maggiore quanto più n risulta maggiore di 1, valore che ha nel vuoto; ciò vuol dire che nell’aria, dove n è circa 1, il coefficiente di trascinamento è praticamente nullo e quindi w = 0. Questo ultimo valore è proprio quello che la luce dovrebbe avere nel vuoto dove n è esattamente uguale ad 1.
La formula di Fresnel ora vista si può interpretare pensando che le cose vanno come se la velocità della luce si sommi solo con una porzione della velocità del prisma e della lente o di qualunque oggetto in moto nell’etere ed, in definitiva, della Terra; questo perché il coefficiente a risulta sempre compreso tra 0 ed 1.
Con l’ipotesi del trascinamento parziale Fresnel riuscì a spiegare tutti i fenomeni che si originavano dal moto di un corpo rifrangente attraverso l’etere ed in particolare l’esperienza di Arago ed il fenomeno dell’aberrazione(32). Rimanevano sull’intera teoria due fondamentali assunzioni che presto o tardi avrebbero richiesto una qualche conferma sperimentale: le onde luminose sono trasversali; l’etere è trascinato parzialmente dai corpi in esso in moto.
Vi era anche qui l’apertura ad una mole di lavori che porteranno, attraverso le misure di Fizeau e Foucalt della velocità della luce, ai lavori di Michelson e Morley ed a colui che fece una mirabile sintesi di tantissime problematiche, Albert Einstein.
NOTE
(1) Ampère, André-Marie. Communication scientifique d’Ampère à 13 ans, 1788.
Ampère, André-Marie. Considérations sur la théorie mathématique du jeu, 1802. (En ligne sur Gallica2)
Ampère, André-Marie. Problème des quadratures. Rapport à l’académie royale des sciences, sur le mémoire de M. Bérard, inséré à la page 110 du VII.e volume de ce recueil, 1817-1818. (En ligne sur Numdam)
Ampère, André-Marie. Discours d’entrée à l’École centrale, à Bourg, 1802.
Ampère, André-Marie. Mémoire sur la détermination de la surface courbe des ondes lumineuses dans un milieu dont l’élasticité est différente suivant les trois directions principales…, 1828. (En ligne sur Gallica)
(2) Tutta la Corrispondenza di Ampère è pubblicata in http://www.ampere.cnrs.fr/ dove si possono trovare molte notizie sulla sua vita e la raccolta delle sue pubblicazioni.
(3) Una trattazione più completa e dettagliata di questa parte, la si può trovare nel mio Concezioni particellari nel XVII e XVIII secolo. La “crisi” dell’azione a distanza.
(4) I lavori di Schelling a cui mi riferisco: Idee per una filosofia della natura (1797), Progetto di un sistema di filosofia della natura ... (1799), Deduzione generale del processo dinamico o delle categorie della fisica (1800), Sulla vera essenza della filosofia della natura … (1801).
(5) Oersted, Hans-Christian, Experimenta circa effectum conflictus electrici in acum magneticam, 21 luglio 1820. Pubblicata in francese: Expériences sur l’effet du conflict électrique sur l’aiguille aimantée. Annales de chimie et de physique, 1820, vol. 14, p. 417-425 . E’ utile ricordare un precedente importante, quello del giurista e filosofo Gian Domenico Romagnosi (1761-1835) che 18 anni prima di Oersted, nel 1820, fece il medesimo esperimento a Trento pubblicando i risultati nei quotidiani di Trento e Rovereto ed inviandolo per il premio di galvanismo istituito da Napoleone all’Académie des Sciences di Parigi. Purtroppo non vi fu nessuno, all’epoca, a cogliere l’importanza di tale lavoro che venne semplicemente nonm preso in considerazione. Lo stesso Oersted, nel 1830, scrisse sull’Enciclopedia di Edinburgo che “la conoscenza dei lavori di Romagnosi avrebbe anticipato la scoperta dell’elettro-magnetismo di 18 anni“.

Il manoscritto di Romagnosi inviato all’Académie des Sciences.
(6) Le note furono lette nei giorni: 18 e 25 settembre; 9, 16 e 30 ottobre; 6 novembre. Il sunto di queste note fu pubblicato negli Annales de Chimie et de Physique (2), t. XV, p. 59/76 e 170/218 nell’anno 1820 sotto il titolo De l’action excercée sur un courant électrique par un autre courant, le globe terrestre ou un aimant. C’è da notare che tutte le memorie di Ampère dal 1820 al 1825 furono raccolte in volume nel 1827 sotto il titolo: Memoire sur la théorie matematique des phénomènes électrodynamiques uniquement deduit de l’expérience. Di seguito riporto l’elenco di alcune memorie di Ampère su questioni elettromagnetiche che si trovano in rete:
Ampère, André-Marie. Mémoire sur les effets des courants électriques, 1820.
Ampère, André-Marie. Recueil d’observations électro-dynamiques, 1822. (document PDF, en ligne sur Gallica)
Ampère, André-Marie, Babinet, Jacques. Exposé des nouvelles découvertes sur l’électricité et le magnétisme…, 1822. (En ligne sur Google “Recherche de Livres”)
Ampère, André-Marie. Exposé méthodique des phénomènes électro-dynamiques et des lois de ces phénomènes, 1823. (En ligne sur Gallica)
Ampère, André-Marie. Description d’un appareil électro-dynamique construit par M. Ampère, 1824. (En ligne sur Gallica)
Ampère, André-Marie. Théorie mathématique des phénomènes électro-dynamiques uniquement déduite de l’expérience, 1827. (document PDF, en ligne sur Gallica)
Ampère, André-Marie. Mémoire sur l’action mutuelle d’un conducteur voltaïque et d’un aimant, 1828. (En ligne sur Gallica)
(7) Le memorie furono lette il 30 ottobre ed il 18 dicembre e non furono mai pubblicate (a parte un brevissimo sunto, Note sur le Magnétisme de la pile de Volta, negli Annales de Chimie et de Physique (2) t. XV, p. 222, 1820 ed il resoconto di una dissertazione tenuta in una seduta pubblica dell’Académie pubblicato sul Journal des Savants del 1821 alla pag. 221). Una esposizione dettagliata dei lavori di Biot e Savart fu da loro eseguita nella terza edizione del Précis élémentaire de Physique, t.II, p. 704 e segg; 1823 (una esposizione più breve si trova sulla seconda edizione della stessa opera, t. II, p. 117 e segg; 1821).
(8) Vedi Précis élémentaire de Physique, citata in nota precedente, p. 737 e segg.
(9) Annales de Chimie et de Physique (2), t. XV, p. 71; 1820
(10) Lo sviluppo di tutto il processo analitico che porta a questa relazione è sviluppato da Whittaker, Vol. 1, pagg. 84-87. Naturalmente gli stessi calcoli sono nel lavoro originale di Ampère Théorie mathématique des phénomènes électro-dynamiques uniquement déduite de l’expérience.
(11) Una volta per tutte devo dare un riferimento linguistico. La parola elettromagnetismo è sinonimo della parola elettrodinamica. La prima nasce nella tradizione inglese mentre la seconda nella tradizione tedesca. Io userò indifferentemente l’una o l’altra.
(12) Arago, Dominique François Jean, Expériences relatives à l’aimantation du fer et de l’acier par l’action du courant voltaïque, Annales de chimie et de physique, vol. 15, p. 93-102, 1820.
(13) Borda, Verdun de la Crenne, Pingré, Voyage fait par ordre du roi en 1771 et 1772, en diverses parties de l’Europe et de l’Amérique, pour vérifier l’utilité de plusieurs méthodes et instruments servant à déterminer la latitude et la longitude, etc. 1778.
Borda, Description et usage du cercle à réflexion. 1778.
(14) G. Monge, Mémoire sur le phénomène d’Optique, connu sous le nom de Mirage, Décade égyptienne, 1, an VII-1799, pp. 37-46; riedito in Mémoires sur l’Égypte, 1, 1800, pp. 64-78.
(15) Nella prima memoria, Traité d’optique analytique (Journal de l’École polytechnique, 14ème cahier, t. VII, avril 1808, p. 1-44 et p. 84-129), Malus sviluppò un’ottica tridimensionale che gli fu poi molto utile per interpretare e sviluppare le successive scoperte. La seconda memoria, Sur la mesure du pouvoir réfringent des corps opaques (Journal de l’École polytechnique, 15ème cahier, t. VIII, décembre 1809, p. 219-228), contiene la legge di Malus che fornisce la misura dell’intensità del fascio emergente in funzione di quello incidente.
(16) L’Institut de France fu fondato durante la Rivoluzione nel 1795. Per quanto dirò nel seguito è utile sapere che nel 1801 integrò i membri dell’Institut d’Égypte fondato da Napoleone durante la sua spedizione in Egitto nel 1798 e chiuso nel 1801 quando i francesi furono sconfitti dagli inglesi. Le prime cariche dell’Institut d’Égypte furono così assegnate: Monge presidente, Bonaparte vicepresidente e Fourier segretario. Esso era diviso in quattro classi: I. Mathématiques; II. Physique et Histoire Naturelle; III. Economie politique; IV. Littérature et beaux-arts (l’Institut de France, invece, comprendeva tre classi: I. Sciences Physiques et mathématiques; II. Sciences morales et politiques; III. Littérature et beaux-arts e, si può notare, l’avanzamento del nuovo Istituto rispetto al precedente. Non è infatti banale la separazione tra la matematica e le scienze naturali). Era stato Bonaparte a volere portare con sé il meglio della cultura francese deell’epoca con il fine di riportarla dove era nata. Quindi Monge ebbe un ruolo importante nella spedizione ed egli portò con sé vari membri della Commission des Sciences et des Arts tra cui (i più noti in ambito scientifico) Berthollet, Fourier, Geoffroy Saint-Hilaire, Malus.
(17) E. L. Malus, Sur une propriété de la lumière réfléchie par les corps diaphanes, Nouveau Bulletin des sciences par la Société philomathique de Paris, N° 16, Janvier 1809, p. 266-269. Malus scriverà ancora un’importante memoria sull’argomento, Sur les phénomènes qui dépendent des formes des molécules de la lumière, Nouveau Bulletin des sciences par la Société philomathique de Paris, N° 20, Mai 1809, p. 341-344 et N° 21, Juin1809, p. 353-355. In quest’ultima memoria Malus assimilò la molecola di luce a un magnete in accordo con la fisica di Newton.
(18) E. L. Malus, Théorie de la double réfraction de la lumière dans les substances cristallisés, Garnery, Baudouin; Paris 1810.
(19) P. S. Laplace, Sur la double réfraction de la lumière dans les cristaux diaphanes, Nouveau Bulletin des sciences par la Société philomathique de Paris, N° 18, Mars 1809, p. 303-310.
(20) A. Fresnel, Mémoire sur la diffraction de la lumière: ou l’on examine particulierement le phenomenes des franges colorees que presentent les ombres des corp eclairees par un point lumineux, Annales de Chimie et de Physique, t. X., 288, pp. 339-475, 1819. Depositato all’Institut il 29 luglio 1818 ed aggiunte successivamente e prima della pubblicazione due note: la prima per un calcolo dell’intensità della luce; la seconda per la spiegazione della rifrazione nella teoria ondulatoria.
E’ da notare che Fresnel non amava particolarmente la fisica, contrariamente alla matematica. Era di salute cagionevole e preferì ritirarsi nella casa paterna in un paesino vicino Caen dove si dedicò a studiare questioni teoriche di vario tipo. Ad un certo punto iniziò ad interessarsi dei fenomeni luminosi. Era riuscito ad entrare in corrispondenza con Arago il quale gli consigliava vari scritti di Newton, di Grimaldi, di Young, … ma il nostro non conosceva né latino, né inglese. Abbiamo una sua lettera del 15 maggio 1814 in cui chiede al fratello Léonor di procurargli un qualche scritto che gli spieghi cosa sarebbe la polarizzazione di cui ha sentito parlare: «Vorrei avere anche qualche memoria che mi mettesse al corrente delle scoperte dei fisici francesi sulla polarizzazione della luce. Ho visto nel «Monitore », qualche mese fa, che Biot aveva letto all’Istituto una memoria molto interessante sulla polarizzazione della luce. Ho un bel rompermi la testa, ma non indovino che cosa sia». La lettera mostra che ancora nel 1814 Fresnel sapeva quasi nulla di ottica. Come ci racconta Ronchi, “lontano dai grandi centri, privo di libri, privo di mezzi sperimentali (racconta di essersi fatto fare dal fabbro del villaggio il micrometro con cui eseguì le prime misure sulla diffrazione), disturbato dalla salute cagionevole, agitato dalle vicende politiche e burocratiche [era un realista in ambienti repubblicani, ndr], non si può proprio dire che egli fosse nelle migliori condizioni per lavorare tranquillamente e serenamente. Invece proprio in queste condizioni egli poté trovare quella serenità, di spirito, quella indipendenza dai preconcetti, che, tante volte, è la chiave migliore per risolvere i problemi che più affaticano la mente umana”. Appena un anno dopo (15 ottobre 1815) Fresnel già presentava all’Académie la sue due prime memorie sui fenomeni luminosi, una sull’interferenza e l’altra sulla teoria dei colori che compaiono su una superficie rigata e che Fraunhofer, dieci anni più tardi chiamerà reticolo. Inoltre, nel 1816 presentò all’Académie una memoria (Annales de Chimie, 2, i, p. 239, 1816) in cui avanzava una teoria simile a quella di Young per spiegare le frange d’interferenza. Per la prima volta si inizia ad intravedere il ruolo della differenza di fase per interpretare l’interferenza. Tale memoria ebbe un supplemento presentato il 15 luglio 1816 nel quale, per la prima volta, gli effetti della diffrazione sono riferiti alla interferenza mutua delle onde secondarie emesse da quelle porzioni dell’originario fronte d’onda che non avevano subito ostacolo dal reticolo di diffrazione. Questo supplemento di memoria fu elaborato nei conti nei successivi due anni e fu quello che originò la memoria di inizio nota che fu poi premiata dall’Académie. Prima di tale memoria però, Fresnel ne presentò un’altra (30 marzo 1818) a l’Académie des sciences de l’Institut de France, è la Mémoire sur les couleurs développée dans des fluides homogènes.
Successivamente Fresnel presentò altre memorie all’Académie, tra cui:
Mémoire sur la réflexion de la lumière, 15 novembre 1819.
Mémoire sur la double réfraction, 26 novembre 1821.
Mémoire sur la loi des modifications que la réflexion imprime à la lumière polarisée, 7 gennaio 1823.
Oltre all’Acadèmie, Fresnel inviava suoi lavori anche ad altre istituzioni che avevano loro riviste. Tra queste memorie merita di essere citata:
Mémoire sur un nouveau système d’eclairage des phares, dicembre 1822.
(21) F. Arago, A. Fresnel, Annales de Chimie, 10, 1919 (questa memoria come molte altre fu pubblicata molto dopo la sua comunicazione).
(22) Young, Miscellaneous Works, 1:383. In questa lettera del 12 gennaio 1817, tra l’altro, si dice: «I have been reflecting on the possibility of giving an imperfect explanation of the affection of light which constitutes polarisation, without departing from the genuine doctrine of undulations. It is a principle in this theory, that all undulations are simply propagated through homogeneous mediums in concentric spherical surfaces like the undulations of sound, consisting simply in the direct and retrograde motions of the particles in the direction of the radius, with their concomitant condensation and rarefactions. And yet it is possible to explain in this theory a transverse vibration, propagated also in the direction of the radius, and with equal velocity, the motions of the particles being in certain constant direction with respect to that radius; and this is a polarisation». A questa prima lettera ne seguì un’altra del 29 aprile 1818. In essa Young esemplificava le vibrazioni trasversali delle onde luminose a quelle che si possono generare su una corda tesa ai suoi estremi.
(23) A. Fresnel, Annales de Chimie, 17, p. 180, 1821.
(24) A. Fresnel, Annales de Chimie, IX, p. 57, 1818.
(25) F. Arago, Mémoire sur la vitesse de la lumière, Comptes Rendus Comunicati all’Institut nel 1810 ma pubblicati molto più tardi, in due parti: 8, p. 326, 1839 e 36, p. 38, 1853.
(26) Fresnel si sta qui riferendo all’ipotesi di trascinamento totale dell’etere da parte della Terra, ipotesi con la quale, come dice subito dopo, risulta inspiegabile il fenomeno dell’aberrazione.
(27) A. J. Fresnel, Sur l’influence du mouvement terrestre dans quelques phénomènes d’optique, Annales de chimie et de physique; 9; pagg. 57-66; 1818.
(28) L’ipotesi in oggetto prevede che l’etere sia in riposo assoluto nel vuoto; in riposo quasi assoluto nell’aria, qualunque sia la velocità di cui quest’aria è dotata; parzialmente trascinato dai corpi rifrangenti.
(29) E precisamente quello che si condensa intorno alle sue molecole e che costituisce la quantità in più di etere contenuto nella Terra rispetto a quella che si avrebbe in una uguale pozione di spazio vuoto. Cioè, secondo Fresnel, si ha una maggiore densità di etere nella materia di quanta se ne abbia nello spazio vuoto; nel moto di un corpo nell’etere esso tende a perdere la massa di etere che ha in più (rispetto a quella che si avrebbe in un uguale spazio vuoto) rimpiazzandola via via con dell’altra presa dallo spazio circostante. In questo modo si origina un parziale vento d’etere, all’interno del corpo, che ha verso contrario al moto del corpo stesso. Fu G. G. Stokes che nella sua memoria On the Aberration of Light (Phil. Mag. , 27; 1845) sviluppò una teoria basata su due assunzioni fondamentali: a) il moto dell’etere è dotato di una velocità potenziale (l’etere è incompressibile ed in esso non si originano vortici); b) L’etere che sta all’interno dei corpi materiali partecipa totalmente al loro moto; così la Terra si trascina tutto l’etere che ha al suo interno e quello che ha nelle immediate vicinanze; questo moto dell’etere va via via decrescendo finché, nelle zone più lontane dello spazio, esso è totalmente in quiete (teoria del trascinamento totale dell’etere). Poste le cose così, in modo abbastanza semplice, si riesce a spiegare, ad esempio, il risultato negativo dell’esperienza di Arago (e di tutte le altre dello stesso tipo), infatti le cose vanno sulla Terra come se essa fosse immobile nello spazio. Una difficoltà molto grossa di questa teoria, come dice Born, stava nella sua incapacità di “spiegare come mai la luce proveniente dalla stella non subisca variazioni di direzione e di velocità nell’attraversare lo strato che separa l’etere dello spazio dall’etere trascinato dalla Terra. Stokes fece un’ipotesi che tenesse conto di tutte le condizioni imposte dalle leggi dell’ottica; ma, come si vide in seguito, essa si dimostrò in contrasto con le leggi della meccanica“. In definitiva l’ipotesi del trascinamento totale incontrava gravi difficoltà nella spiegazione del fenomeno dell’aberrazione; ovviamente non riuscì a rendere conto dell’esperienza di Fizeau che invece ben si raccordava con l’ipotesi del trascinamento parziale di Fresnel; infine, per l’aver introdotto ipotesi in contrasto con le leggi della meccanica (come dimostrerà H.A. Lorentz nel 1886), fu presto abbandonata.
(30) Si ricordi che l’indice di rifrazione n è definito come il rapporto della velocità c della luce nel vuoto (nell’etere) con quella c1 della luce nel mezzo materiale: c/c1 = n => c1 = c/n. E’ importante notare che, da considerazioni relative all’aberrazione stellare, Fresnel fece l’ipotesi che il risultato negativo dell’esperienza di Arago non dipendesse dal prisma in sé, che esso fosse cioè indipendente dalla natura del mezzo rifrangente.
(31) Per approfondire questa parte si può vedere Born, pagg. 167-173.
(32) Questo almeno al 1° ordine del rapporto v/c. In ogni caso la strumentazione dell’epoca non avrebbe mai permesso di apprezzare effetti al 2° ordine ( v2 / c2). Occorre notare che il fenomeno dell’aberrazione trovava una soddisfacente spiegazione anche nell’ipotesi di etere immobile, mentre era spiegato con difficoltà dall’ipotesi di trascinamento totale. L’esperienza di Arago invece era spiegata solo dall’ipotesi di trascinamento parziale dell’etere.
BIBLIOGRAFIA
(1) A.Baracca, R. Livi – Natura e storia: fisica e sviluppo del capitalismo
nell’0ttocento – D’Anna, 1976.
(2) E. Cassirer – La filosofia dell’illuminismo – La Nuova Italia, 1973.
(3) E. Bellone – Il mondo di carta – EST Mondadori 1976.
(4) J. D. Bernal – Storia della scienza – Editori Riuniti 1965.
(5) R. Taton (diretta da) – Storia generale delle scienze – Casini 1965.
(6) L. Geymonat (diretta da) – Storia del pensiero filosofico e scientifico – Garzanti 1971.
(7) P. Rossi (diretta da) – Storia della scienza – Utet 1988.
(8) A. M. Ampère – Opere (a cura di M. Bartolini) – Utet 1969.
(9) Salvo D’Agostino – L’elettromagnetismo classico – Sansoni 1975.
(10) E. Whittaker – A History of Theories of Aether and Electricity – Nelson & Sons 1954.
(11) V. Ronchi, Storia della luce, Zanichelli 1939.
(12) M. Born – La sintesi einsteniana – Boringhieri 1965. (L’opera è del 1920).
(13) http://web.unife.it/cdl/castelli/rivista/anno4/cardinali.pdf
Categorie:Senza categoria
Rispondi