Roberto Renzetti

(Aprile 2009)

ALCUNI DATI BIOGRAFICI

        Giovan Battista Baliani (o Baliano) nacque a Genova nel 1582 da una famiglia patrizia. Non si hanno molte notizie del giovane Baliani ma, vista la grande simpatia che la nobiltà genovese mostrò verso la Compagnia di Gesù tanto da chiedere nel 1547 a Ignazio de Loyola l’istituzione a Genova di una scuola che fu poi aperta nel 1554 (il Collegio dei Gesuiti), è da immaginare che studiasse in quella scuola che estese la propria attività a studi universitari nel 1604. Senza particolari problemi economici anche perché i Signori genovesi che avevano insistentemente richiesto la scuola si rifiutarono poi di pagarla affidandosi solo a private liberalità. Baliani terminò comunque presumibilmente in tale scuola gli studi in ambito scientifico (matematica e fisica). Dico ciò anche se nel Collegio genovese il settore delle discipline scientifiche non fu particolarmente curato per la cronica mancanza di insegnanti di tali discipline. Padre Bernardino Salino, che fu nominato lettore di matematica nel Collegio di Genova nel 1604, scriveva a Cristoforo Clavio pregandolo di inviare da Roma testi scientifici: perché mai altre volte si è letta questa scienzia in questo luogo, per questo ho trovato il collegio sfornito di libri e di istromenti necesari per questa professione. D’altra parte Genova non aveva brillato in ambito scientifico nei secoli in cui Firenze, Pisa, Padova, Venezia ed altri centri culturali italiani davano i loro grandi contributi. Ancora alla metà del Seicento, come annotava  il gesuita P. Sonderegher era potius civitas Mercurio quam Patri Pieridum dicata, dedita cioè maggiormente allo scambio di merci e di materiali che allo studio e alla cultura. Ed il giudizio era lo stesso di Giacomo Bonvicino, insegnante di matematica nel collegio dei Gesuiti: Genova non è città di scienze: i grandi attendono a negotii e cambi, i giovani a dame e balli […] tanto si ammette al governo un ignorante, quanto uno scienziato […]. Molti ingegni di questa città preferirono andare a lavorare in altre città italiane o addirittura all’estero, come Gian Domenico Cassini che passò a Bologna prima di andare a Parigi (anche il gesuita Orazio Grassi, coetaneo e conterraneo del Baliani, essendo nato a Savona nel 1583, e che avrà una storia di polemiche con Galileo, era andato a studiare al Collegio Romano). Anche perché, caso unico tra le città dell’importanza di Genova, in questa città, fino alla creazione di quella dei Gesuiti nel 1604, non vi era alcuna Università. Maggiore quindi il merito del giovane Baliani che, come accennato, dovette terminare i suoi studi nel Collegio dei Gesuiti (probabilmente anche in quella Università aperta proprio in tempo utile per la sua età) ed in questo ambiente il suo corso di studi per poi accedere, come d’uopo per un patrizio, all’assunzione di una qualche responsabilità politica nella gestione della Repubblica. Il primo incarico lo ebbe nel 1611 e fu quello di Prefetto della rocca di Savona. Nel 1623 ottenne l’incarico di Governatore della città di Sarzana, quindi nel 1624 fu nominato al Senato della Repubblica di Genova. Come Senatore nel 1626 ottenne l’incarico di fare da sovrintendente scientifico ad una grande impresa: la costruzione di una muraglia (le Mura Nuove) che doveva difendere la città dal lato terra (una sorta di triangolo equilatero con un lato sul mare e gli altri due di una lunghezza complessiva di circa 13 chilometri). A Baliani venne affidato il compito di calcolare e verificare sul posto ogni angolo saliente o rientrante dei bastioni, la distanza tra un bastione e l’altro e la loro lunghezza, che a Genova per la prima volta nella storia dell’architettura militare, assunse una notevole dimensione. Con l’importante suo contributo Genova divenne una città all’avanguardia nell’architettura militare, modello per le scuole francese e tedesca. La costruzione delle Mura Nuove, con qualche breve interruzione nei lavori, terminò nel 1633. Intanto, nel 1630, Baliani ebbe dal Governo della Repubblica l’incarico, dopo averne verificato il grado con adeguati scandagli, di rimediare gli eventuali problemi di insabbiamento del porto della città nelle cui acque arrivavano i detriti dei torrenti Bisagno e Polcevera. Quella città, con poca tradizione scientifica per suo maggiore interesse in affari, proprio per questi ultimi, si trovò ad essere, nei primi anni del Seicento, la promotrice di varie imprese scientifiche come quelle citate (mura e porto) e quella della costruzione di un acquedotto per l’approvvigionamento idrico della città, della quale discuterò più oltre. Per concludere con le cariche politiche che crescevano anche per i meriti accumulati sul campo, Baliani, dal 1647 al 1649, fu ancora a Savona ma come Governatore e, contemporaneamente, fu Capitano degli arcieri della Repubblica che avevano sede nell’imponente Fortezza di Priamar nella stessa Savona.

        Quindi Baliani, anche filosofo, letterato ed uomo d’affari, e nonostante la Repubblica di Genova non considerasse che attività a fini pratici^(1), ebbe un’intensa attività pubblica che si coniugò con l’attività di ingegnere civile e militare e con una importante attività di scienziato che scaturiva da tutti i problemi pratici che dovette risolvere e per i quali era indispensabile aggiungere alla fase empirica quella teorica e sperimentale.

        Baliani si spense a Genova nel 1666.

I PRIMI INTERESSI SCIENTIFICI

        Un documento importante sugli interessi scientifici di Baliani è una prima lettera che Galileo gli scrive  il 25 gennaio 1614 (Galileo ha 50 anni e Baliani 32). Questa lettera discendeva da due precedenti lettere che l’amico di Galileo, Filippo Salviati⁽²⁾, gli aveva inviato come presentazione del medesimo Baliani. La prima di queste due lettere è del 27 dicembre 1613 e proveniva da Genova. Scriveva Salviati a Galileo:

Ho trovato qua un filosofo alla usanza nostra, garbatissimo gentil huomo, nominato il S.r Gio. Batista Baliani. Lui filosofa sopra la natura, si ride di Aristotile et di tutti i Peripatici. È buon geometra, et m’ ha detto che andò a Venetia aposta per vedere V. S. Si ride di chi ha scritto contro al vostro libretto, sebene m’ ha detto che ha notate alcune cose nel libro di V. S. che non gli piacciano; et io l’ ho pregato che me le mostri, il che m’ ha promesso fare, ma dice che ha il libro in villa. Cercherò me le mostri, per vedere, se è possibile, resti satisfatto. È per la buona quanto huomo che habbia mai trovato, ma è un poco di sua opinione; nel resto, garbatissimo et da piacere a V. S., et non desidera altro se non una conversatione di filosofi liberi.

E’ una presentazione molto buona basata sul ridersi di Aristotele. A questa lettera Salviati ne faceva seguire un’altra in data 13 gennaio 1614 nella quale si entrava in argomento:

Dissi al S.r Gio. Batista Baliano quanto la mi scriveva per conto di pesar l’ aria. Mi rispose che desidera grandemente, con comodità di V. S., di saper il modo, o almeno quanto l’aria pesa respetto all’ acqua. Di gratia, V. S., quando sarà disoccupata, gli scriva et gli dia qualche sodisfatione, perché è gentil huomo garbato et stima assai V. S. È filosofo libero et ha molta opinione di V. S., et a molte cose m’ ha dato l’istesse ragioni che ho intese da lei; et se trattassi con V. S., in pochi giorni converresti in ogni cosa. Se la gli scrive, gli dia del molto Ill. solamente.
A me non risponda, perché le lettere non mi ci troveriano. Et baciandoli le mani, la prego a far mie racomandationi a’ soliti, con dirli se vogliono niente di Spagna, me lo avisino.

L’argomento che indicava Salviati a Galileo era relativo al peso dell’aria, problema che, evidentemente, era stato argomento di discussione tra lo stesso Salviati e Galileo. Della qual cosa Salviati doveva aver parlato a Baliani e quest’ultimo chiedeva di saperne di più.  Galileo si mise subito in contatto con chi gli indicava l’amico con questa lettera del 25 gennaio 1614:

Molto Ill.re Sig.r et P.ron Oss.mo

L’ Ill.mo Sig.r Filippo Salviati con le sue ultime lettere mi ha significato, come V. S. desiderava di veder certe mie lettere intorno alle macchie solari, le quali con questa gl’ invio, sebene è lettura assai popolare e indegna dell’ orecchie di V. S., non mi havendo porto il finto Apelle ⁽³⁾ occasione di troppo sottilizzare, come ella dalle sue lettere comprenderà. Forse in breve, con opportuna occasione, tratterò questo medesimo argomento più esattamente. Il medesimo Signor mi scrisse, più giorni sono, come V. S. haveva veduto quel mio trattatello delle cose che stanno sul’ acqua, scritto, com’ Ella vede,  incidentemente; nel quale intendo che V. S. ha alcune cose che non gli satisfanno interamente, le quali io la supplico a conferirmi, assicurandola che io riceverò per maggior favore le censure di quelle cose che non gli piacessero, che l’assenso o le lodi del resto, poi che quelle saranno di mio utile, e non queste. Al medesimo Signor mandai un modo, delli tre che ne ho, di pesar l’aria, acciò lo conferisse con V. S.; ma perchè non so se la mia lettera sarà giunta avanti la sua partita, potrà V. S. farmene avvisato, acciò, in difetto di quella, le passi supplire con altra al comandamento di V. S.
Il Sig. Filippo, al quale ho conferito buona parte delle mie immaginazioni filosofiche, mi scrive haver trovato gran conformità tra le sue speculazioni e le mie; di che io non mi sono molto maravig1iato, poiché studiamo sopra il medesimo libro e con i medesimi fondamenti.
Restami di dovere offerirmi a V. S., il che fa con ogni affetto di cuore e sincerità di animo; e la prego a gradire tale mio affetto et a darmene segno col comandarmi e col conferirmi alcuna delle sue contemplazioni: il che riceverò per gratia singolare. E con questo gli bacio le mani, come fa anche al Sig. Giovanni Batista Pinelli, mio antico padrone; e dal Signor Dio gli prego somma felicità.

Galileo era estremamente cortese e disponibile. Chiedeva a Baliani che gli dicesse su cosa non era d’accordo e si diceva pronto a dare le spiegazioni che eventualmente gli fossero richieste. Baliani non aspettava altro ed in tempi brevissimi, il 31 gennaio 1614, scrisse a Galileo una lunga lettera. Nella prima parte, dopo aver ringraziato Salviati per avergli dato l’opportunità di conoscerlo, si presentava come sostenitore del nuovo modo di fare scienza affermando che, anche se è un principiante, è:

[…]  amico delle scienze e per conseguenza di chi le possiede, quale ho conosciuto prima d’ hora essere V. S. in quel suo dottissimo trattato delle cose che stanno su l’acqua, e di presente nelle Lettere che mi ha favorito mandarmi, che trattano delle macchie del sole: nelle quali cose tutte si scorgon infinite, bellissime e nuove oppinioni filosofiche, provate con sotilissime dimostrationi geometriche; senza le quali la filosofia non merita il nome di scienza, ma più tosto d’oppinione. Et invero io mi son sempre riso di tutte le conclusioni filosofiche, che non dipendano (oltre quelle che sappiamo esser vere per lume di fede) o da dimostrationi matematiche o da esperienze infallibili; e se pochi si sono ritrovati sin al dì d’ hoggi che habbian filosofato in cotal maniera, ciò è per avventura avvenuto per esservi pochi che habbiano piena contezza delle due sudette scienze […].

        Non era usuale in questo periodo trovare dei sostenitori del metodo scientifico, qualcuno che sostenesse che l’osservazione di un fenomeno se non accompagnata da un trattamento teorico non serviva a molto. Ma Baliani aggiungeva un qualcosa che è di grande interesse in ogni periodo della storia: sono pochi coloro che hanno acquistato il modo corretto di disquisire sulle questioni naturali perché sono pochi coloro che hanno dimestichezza con la matematica e con il modo di sperimentare.

        Dopo questa premessa Baliani entrava in argomento su due questioni. La prima era una discussione sulle macchie solari, con continui riferimenti a punti precisi del lavoro di Galileo in proposito, Istoria e dimostrazioni intorno alle macchie solari e loro accidenti (1613), in particolare al moto che Galileo assegnava al Sole:

Non posso negare di non haver un poco di difficoltà a conceder quel che V. S dice […] del moto del sole⁽⁴⁾: perchè, tutto che si concedesse che la nave mossa, a cui si togliessero gli impedimenti estrinseci, si havesse a muover sempre, non ne séguita, s’io non m’inganno, che il sole si habbia sempre a muover, poiché non par necessario conceder che l’ambiente non gli debba dare qualche piccolo impedimento; né basta, per mio aviso, d’ir che anche egli se ne muova. poiché l’aria, che è intorno ad una ruota che gira, si muove anch’ essa per lo moto di lei, né perciò credo che V. S. stimi che non le dia qualche puoco trattenimento.

Sulle macchie solari altre questioni nascevano sul fatto che gli astri avessero delle superfici opache e ruvide e sulla possibilità che le macchie fossero legate al maggiore o minore calore che il Sole invia sulla Terra e quindi alla loro influenza sul clima (per il fatto che una macchia è una zona da cui non si dipartono i raggi solari). La seconda era relativa ad un dubbio che aveva avuto leggendo il Discorso intorno alle cose che stanno in su l’acqua, o che in quella si muovono (1612) relativo al fatto che, secondo quanto comunemente si riteneva, il ghiaccio dovrebbe essere acqua condensata con tutte le conseguenze di ciò. La cosa non gli tornava perché una materia condensata ha maggior peso dell’acqua e quindi, invece di galleggiare, deve andare a fondo. Ma il dubbio glielo aveva già chiarito Salviati

dicendomi che il giacchio occupa maggior luogo dell’acqua: il che io poi anche provai per isperienza, e gli dissi la mia oppenione, come possa essere che il giacchio si faccia dal freddo che condensi l’ acqua e che ad ogni modo egli occupi maggior luogo; perchè si condensa non uniformemente, ma più tosto in diverse parti, fra le quali restano delle parti più rare, onde egli tutto insieme viene ad essere più raro dell’ acqua, la qual difformità de parti è caggione che il giacchio perda in gran parte la diafaneità […]

Restavano in sospeso due questioni che Baliani chiedeva a Galileo. La prima è in una domanda sull’eventuale osservazione di Galileo di una nova nella costellazione del Cigno:

Vorrei sapere se V. S., che ha ricercato così diligentemente tutte le regioni celesti, ha per avventura osservata col canone, o sie telescopio, la stella nuova che è nel petto del Cigno, per vedere se a sorte vi si scorgesse qualche differenza dalle altre stelle. Mi par di vedere che V. S. appruovi le oppenioni del Copernico; e pur io crederei che le osservationi che si fanno col cannone circa Venere e le Stelle Medicee e le macchie del sole più tosto provassero la flussibilità della materia celeste, onde par che più tosto venga ad essere più provabile 1’opinion del Ticone.

Era proprio convinto Galileo del sistema copernicano ? Non sembrava più probabile, dalle osservazioni indicate, quello di Tycho ?

        L’ultima questione era quella del peso dell’aria rispetto all’acqua, poiché Salviati era già partito non aveva avuto risposta al quesito già avanzato.

        Infine Baliani informava Galileo di una sua esperienza relativa alla produzione di calore mediante lo sfregamento di due metalli, tanto calore in grado di cuocere degli alimenti:

E perchè V. S. mi dice ch’ io le scriva qualcheduna delle mie speculationi, come che io habbia fatto puoco di buono, le dirò solo per hora che ho novamente ritrovato un modo, a parer mio nuovo, di cuocere senza fuoco, mediante il moto di due ferri che si riscaldano insieme; e fattane l’esperienza (sebene assai imperfettamente), m’è riuscita assai bene. Procurerò di farla di nuovo meglio; e questo et ogni altra cosa mia sarà sempre a’ suoi comandi, poichè, come già le ho detto, V. S. può valersi d’ogni mia cosa e di me stesso; e mi serà gran favore, sempre che si compiacierà di farlo.

        Il 12 marzo arrivò la risposta di Galileo, altrettanto lunga ed articolata. Galileo iniziava con le scuse per il ritardo nella risposta dovuta a sue condizioni di salute quindi, dopo aver ringraziato Baliani per aver letto con attenzione i suoi lavori, passava a rispondere alle questioni sollevate nella precedente lettera di Baliani a cominciare dall’essenza delle macchie solari. Galileo scriveva che in proposito egli non dava nulla per definitivo ma aveva soltanto espresso un’ipotesi tra le mille possibili che noi non possiamo neppure immaginare:

quanto all’ essenza delle macchie solari, io veramente non ardirei mai di affermarne cosa alcuna, se non a quello che par che le si assimiglino, delle cose conosciute da noi: ma a quante più cose hanno similitudine, tanto più è dubbio l’ affermar di loro quel che le siena; oltre che posson esser mille cose ignotisssime a noi.

Sul moto del Sole intorno al proprio asse Galileo spiegava a Baliani una sottile questione logica. Non era che egli non pensasse che potesse esservi un qualche impedimento al Sole da un ambiente immobile che lo circondasse, era solo che, poiché l’ambiente che è intorno al Sole (le macchie) ruota, tanto vale ammettere che lo stesso Sole ruoti:

io veramente non ho hauto intenzione di dir che ‘l corpo solare, rivolgendosi in se stesso, non fusse per ricever qualche impedimento dall’ ambiente che stesse fermo; ma hebbi pensiero di dir che, dato che l’ambiente si girasse intorno al sole, esso ancora da tal rivolgimento sarebbe menato in volta: però V. S. mi favorirà di riveder quel luogo, perchè forse ne potrà cavar questo senso che non ha dell’ improbabile, sì come l’altro sarebbe veramente erroneo.

Sulla sostanza costituente le stelle, Galileo aveva premura di dire che egli faceva grande differenza tra quelle fisse e quelle mobili (i pianeti): le prime devono avere superficie lucida, non trasparente, che emette luce e le seconde devono ricevere la luce dal Sole. Se poi queste seconde sono diafane al loro interno non sapeva dire (anche se si chiedeva perché mai dovevano esserlo) ma certamente la superficie esterna doveva essere rugosa e , ai nostri occhi, opaca come una pietra.

        Galileo accennava poi alla nova della costellazione del Cigno dicendo di non averla osservata quindi si mostrava entusiasta dell’esperienza di produzione di calore mediante lavoro meccanico e manifestava il desiderio di essere informato di ulteriori sviluppi. Vi era poi la questione relativa all’accettazione del sistema astronomico di Tycho o di quello di Copernico e qui Galileo afferma che è decisamente favorevole a Copernico mentre ha vari problemi con il sistema ticonico in particolare quello relativo all’immobilità della Terra:

Quanto all’opinione del Copernico, io veramente la tengo sicura, e non per le sole osservazioni di Venere, delle macchie solari e delle Medicee [i satelliti di Giove che Galileo aveva scoperto, ndr], ma per l’altre sue ragioni, e per molt’altre mie particolari che mi paiono concludenti. […]. Nell’opinione del Ticone mi ci restano quelle massime difficoltà che mi fanno partir da Tolomeo, dove che in Copernico non ho cosa alcuna che mi apporti un minimo scrupolo, e men di tutte le instanze quelle che fa Ticone contro alla mobilità della terra in certe sue lettere.

L’ultimo argomento trattato nella lettera era relativo all’esperienza che Galileo aveva ideato per pesare l’aria rispetto all’acqua. Seguiamo il racconto di Galileo di tale esperienza:

Per pesar l’aria, io piglio un fiasco di vetro AB, grande come la testa d’un huomo incirca, il quale nel collo habbia la strozzatura B, per potervi legar fermamente un ditale di cuoio CD; il qual ditale nel mezo habbia un’animella da pallone ben fermata, per la quale con uno schizzatoio caccio molt’aria nel fiasco AB, havendolo prima pesato in una bilancia esatta; e dopo havervi compressa molt’aria per forza, la quale in virtù dell’animella resta carcerata, torno a pesare il fiasco e trovolo notabilmente più grave: e però salvo appartatamente il peso che bisogna aggiunger di più, il quale vien a esser il peso dell’aria straniera.

E per assicurarmi che non ne vada traspirando punta, metto innanzi nel fiasco un poco d’acqua, e tenendolo sempre. con la bocca in giù m’assicuro che l’aria non può uscire, perchè prima caccerebbe l’acqua et io la vedrei gocciolare. Resta hora che io misuri l’aria estranea. Però piglio un altro simil fiasco EFG, col collo strozzato in F e con un piccol foro in G, e con la bocca che termina sottile, come si vede in E, dove è il foro assai stretto. Questo lo lego nella parte inferiore del ditale, cioè verso D, sì che la punta E risponda, incontro al foro dell’animella; e dopo haverlo saldamente legato, spingo la punta E contro al coperchietto che serra l’ animella; et apertolo, l’aria compressa del vaso AB fa impeto e caccia fuora l’ acqua dell’altro vaso per il foro G, e séguita di cacciarne tanta, quanta è la mole dell’ aria che esce dal vaso AB: e questa è tutta quella che v’ era compressa oltre alla costituzione naturale. Salvando dunque l’acqua che verrà fuori del foro G, la peso poi diligentemente, e trovo quanto ella sia multiplice in peso all’ aria che fu pesata nel vaso primo: la quale, per quanto mi ricordo, pesava circa 460 volte più; ma non me n’assicuro. Si può reiterar l’operazione molte volte, per venirne in certezza.

Questa sarà l’ultima lettera di Galileo a Baliani in questo periodo. Probabilmente perché alla sua chiusura Galileo aveva detto di essere affaticato e di non poter diffondersi come avrebbe voluto. Ciò non toglie che Baliani, dopo aver risposto a questa missiva di Galileo il 4 aprile 1614, continuerà a scrivergli. Nella risposta Baliani si diceva soddisfatto delle risposte che oltre a servire a lui per chiarire molte cose, erano d’aiuto a molti genovesi interessati di questioni scientifiche soprattutto di quanto scriveva il medesimo Galileo. Diceva che Galileo, nel suo scritto, non aveva trattato la questione delle macchie solari come responsabili delle variazioni climatiche, era favorevolmente colpito dall’esperienza ideata da Galileo per misurare l’aria e forniva dettagli sul suo modo di produrre calore strofinando due ferri:

e perchè V. S. desidera ch’ io le dica il modo di cuocer senza fuoco io ho fatto far un vaso di ferro col fundo piano, rotondo, di diametro circa una spanna, et un altro ferro, pur rotondo e piano, dell’ istesso diametro, il qual ferro io faccio voltar velocemente, o per mezo d’una ruota grande o di acqua corrente, sopra il quale faccio posare il fundo del detto vaso, che stia ben fermo. Hor donque con lo stropicciarsi insieme si riscaldan tanto i detti due ferri, che si riscalda anche e si cuoce ciò che si pone dentro il vaso.

        Dopo questo scambio epistolare, Baliani pensò bene di recarsi a Pisa e Firenze per conoscere personalmente Galileo (con il quale discusse anche sul problema del moto di caduta dei gravi) e fece un tal viaggio nei primi mesi del 1615 mentre Galileo trattava con il suo amico Federico Cesi per poter iscrivere il Baliani all’Accademia dei Lincei⁽⁵⁾. Alla fine di tale viaggio il 17 giugno 1615 scrisse una lettera a Galileo. Dopo le scuse per non essersi congedato da lui in occasione della partenza da Firenze, scelta fatta per evitare di affaticare Galileo non ancora in buona salute, gli diceva di essere passato per Pisa ed aver ivi incontrato Don Benedetto Castelli ed un tal signore che ha ritrovato il tanto desiderato il moto perpetuo al quale io non credo punto. La lettera prosegue con una dimostrazione che Galileo aveva richiesto a Baliani, di un teorema del matematico francese François Viète (1540-1603), relativo alla proportione della forza che si richiede a tirar su un peso sopra piani variamente inclinati. La dimostrazione era stata richiesta da Galileo perché aveva avuto un qualche sospetto in proposito. Infatti, avutala, si rese conto che quella dimostrazione era sua come pubblicata nel suo Trattato di meccaniche (opera circolante manoscritta ed elaborata a Padova a partire dal 1598) e solo per errore attribuita al Viète. Su questa dimostrazione sorgerà un qualche imbarazzo di Galileo nel 1638 quando riprenderà la corrispondenza tra i due. Il fatto è che nel 1615 egli aveva elaborato la dimostrazione in oggetto ma, con il tempo, l’aveva abbandonata perché superata. Ora su tale dimostrazione Baliani impostava il suo De motu del 1638 e se era vero che quella dimostrazione era di Galileo, ora non era più riconoscibile come tale dopo oltre 20 anni. Tra l’altro Baliani utilizzava la dimostrazione utilizzando il concetto di momento che nella formulazione di Baliani risultava una sorta di sostituto della velocità. Ed il De motu, attraverso il momento, trattava la caduta dei gravi, sia sulla verticale che sui piani inclinati, con il momento, cioè con la velocità o meglio con la velocità costante senza l’introduzione della variazione di velocità nel tempo, cioè dell’accelerazione. Da qui il profondo imbarazzo di Galileo. Queste vicende saranno comunque riviste più oltre, dopo il seguente paragrafo, quando entrerò a discutere dei contenuti del De motu.

        Prima di avere un’altra lettera, una testimonianza cioè dell’attività di Baliani in assenza di altre informazioni, occorre attendere l’8 agosto 1619. In questa lettera Baliani affrontava due problemi: il primo relativo a delle considerazioni che gli erano venute sulla natura del caldo e freddo, il secondo relativo alla natura delle medesime comete, ambedue a seguito della lettura del libro sulle comete di Mario Guiducci, Discorso delle comete (1619), che riprendeva molte teorie di Galileo. A proposito di questo secondo problema Baliani affermava di non essere in grado di vedere quale difficoltà vi fosse nell’ammettere che la cometa è un corpo generato di quell’istessa materia che i pianeti, ma non così ben conglutinata insieme, e perciò facile a dissolversi. Relativamente poi al fatto che la coda della cometa è sempre rivolta in verso opposto alò Sole, Baliani affermava che gli sembrava fin troppo chiaro che la causa di ciò stia nei raggi del sole che per lo corpo della cometa  siano trappassati, il che a’ pianeti non adviene  per la opacità loro. Il primo problema era discusso in modo da mettere in gioco degli ignicoli, delle piccole particelle cioè di fuoco. Il suo ragionamento iniziava dal caldo generato dal movimento de gli orbi celesti, come affermato nel lavoro citato. Partiamo dalla lettura di ciò che scriveva Mario Guiducci:

Ma posto ancora il movimento de gli orbi celesti e ‘l rapimento de’ supremi elementi, io non veggo però come da tale agitazione si possa produr calore e accendimento, più tosto che freddo e spegnimento di fuoco. Né vorrei che noi insieme con Aristotile ci lasciassimo indurre in questo concetto, che ‘l moto abbia facultà d’eccitar calore; perchè tal proposizione è falsa. Ben è vero che una gagliarda compressione e confricazione [sfegamento, ndr] di corpi duri è atta e bastante ad eccitar calore e anche incendio, ben che ella sia fatta con movimento tardissimo: e così le girelle delle taglie insieme co’ canapi s’ abbrucerebbono, mentre nell’ alzare grandissimi pesi, ancor che con moto tardissimo, si soffregano, se col bagnarle non fossero rinfrescate; e se noi con somma velocità faremo andare intorno una grandissima ruota di legno o a’ altra materia, ella non si scalderà punto né nella sua massima circonferenza, dove il moto è velocissimo, né in altra sua parte, ma bene s’ecciterà gran calore nel suo asse, nello stropicciarsi co’ suoi sostegni, benché egli sia molto sottile e però di moto tardissimo sopra ogn’ altra parte di essa ruota; ed i fabbri comprimendo con grave martello un ferro, in pochi colpi il riscaldan sì che ne traggono il fuoco. La compressione e confricazione de’ corpi solidi e duri non è senza moto; ben sono molti moti senza di lei. E perchè dalla compressione, quantunque lentissima, ne veggiamo eccitar calore, ma non già dal moto senza fregagione di corpi duri, benché veloce, perciò l’ effetto dello scaldare dal fregamento si de’ riconoscere, e non dal moto, ancor che Aristotile, avendo più la mira alla falsa immaginazion conceputa ch’ alla sensata esperienza, abbia creduto e scritto che ‘l ferro della freccia tirata con gran velocità s’infocasse. Ma io credo tutto’l contrario, e dico che tirandosi una freccia col ferro molto ben caldo, egli molto più tosto nella somma velocità si raffredderebbe, che tenendolo fermo. […]

Il corpo, dunque, che ha da render calore, bisogna che si vada dissolvendo in sottilissime parti, !e quali, movendosi, penetrano per li meati della nostra carne, e nel passar per essa, secondo che saranno pochi o molti, tardi o veloci, produrranno col lor toccamento in noi un certo grato diletico, che noi poi chiamiamo caldo soave, o vero una violenta dissoluzion di parti con molto nostro dolore, la quale scottamento o abbruciamento vien detta. Ma che più? qual materia si vedrà mai produr calore, se non quando ella si va consumando e in sottilissime parti dissolvendo? I legni, la cera, gli oli, e in somma ogni materia, scaldando si consuma e s’abbrucia.

        Il Guiducci contestava Aristotele in un punto dove il Filosofo aveva scritto cose corrette e Baliani parlava a Galileo di quanto aveva letto perché Guiducci prendeva le mosse dalla teoria fasulla delle comete del Galileo medesimo. E scriveva Baliani a Galileo:

 Intorno [al caldo generato dal moto] dico stimare fundatissima la suoa sentenza, dove crede che qualunque cosa mossa velocemente per l’aria non si riscaldi: anzi mi sono meravigliato di qualche istorici, ma più di Giusto Lipsio che lo confermi nel suo trattato della Militia Romana, dove dicono che le palle di piombo tirate da’ fiondatori romani, per la gran velocità riscaldate si struggeano. Tengo donque per cosa certissima, che non dalla velocità del moto, ma dallo stroppicciamento di due corpi insieme se ne produca il calore. È ben il vero ch’ io non ho ben potuto capire la suoa opinione [su] come si senta il caldo; né posso intendere in che modo quelle sottilissime parti del corpo sminuzzato, penetrando nella nostra carne, si facciano sentire soavemente se sono tarde, con dolore se violenti; perchè vediamo pure, oltre il dolore che produce in noi sì fatta dissolution de parti, produce anche nel corpo che si dissolve quella cosa che dimandiamo fuoco, sia ella sostanza o accidente: del che bisognarebbe pure addurne la cagione, e dimostrare in che modo la detta dissolutione vien prodotta. Et è da notare che se i legni, la cera e l’oli scaldando si consumano, si dissolvono in vapori, cioè a dire in parti molto diverse da quelle ne’ quali è da credere che V. S. presupponga che si dissolvano i ferramenti et altri corpi duri con il fregarsi insieme.

        Insomma si trattava di questioni tutte da discutere e da capire, tanto che lo stesso Galileo scriveva una nota a margine di questa lettera in cui poneva, anche lui, delle domande.

        Dopo questa lettera non abbiamo ulteriori notizie per più di 10 anni⁽⁶⁾.

I PROBLEMI LEGATI ALLA DISTRIBUZIONE DELL’ACQUA

        Per capire il seguito della storia occorre capire a quali problemi doveva far fronte Baliani nella sua attività di ingegnere della Repubblica.

        Sono a tutti noti gli imponenti acquedotti romani. In essi veniva sfruttata la semplice gravità. L’acqua veniva prelevata da una sorgente, fatta scorrere in condotte con generalmente piccole pendenze, fino ad arrivare in serbatoi che si trovavano in punti elevati rispetta alla città che doveva essere servita. La ‘caduta’ da questi serbatoi, oltre a fornire l’acqua per i normali usi, era in grado di alimentare le diverse fontane. Nei secoli successivi alla caduta dell’Impero di Roma, svariati acquedotti risultarono danneggiati e si crearono concentrazioni urbane in luoghi non precedentemente serviti dagli acquedotti di Roma. Si ritornò quindi a metodi primitivi: al trasporto dell’acqua mediante botti nei luoghi di consumo. Nel periodo rinascimentale si iniziarono a riproporre i problemi dell’approvvigionamento continuo di acqua delle città. La situazione era però tale che gli imponenti acquedotti alla romana erano ora praticamente irrealizzabili. Si trattava di approvvigionarsi da fonti relativamente più vicine. Allo scopo iniziò lo sviluppo delle pompe aspiranti e prementi che avevano la funzione di innalzare l’acqua da vicini fiumi fino a raggiungere la città da alimentare che generalmente, per problemi logistici di difesa, era a livelli superiori. Cominciarono a nascere le prime grosse difficoltà: se il dislivello fiume-città era troppo elevato le pompe via via più grandi dovevano spingere l’acqua ad enormi pressioni dentro delle tubature; la ghisa non era in grado di sopportare tali pressioni, il piombo tanto meno, il bronzo sarebbe stato in grado ma costruire acquedotti in bronzo avrebbe rappresentato una follia economica. In attesa degli sviluppi della tecnica metallurgica, sollecitata anche da questi problemi, si preferì lavorare con più pompe: ognuna serviva a raccogliere l’acqua ad un livella di poco più alto, fino a raggiungere la quota desiderata (l’acquedotto che riforniva la reggia ed i giardini di Versailles, realizzate nel 1682, disponeva di 64 pompe operanti sulla riva del fiume, di 79 pompe al primo serbatoio e di 82 pompe al secondo serbatoio; tutte le pompe venivano alimentate dalla stessa energia idraulica).

        Con un problema di questo tipo si imbatté Baliani nel 1630, quando si occupò dell’ampliamento dell’acquedotto di Genova. Si trattava di costruire delle nuove prese, al torrente di Bargagli, al greto del Bisagno con derivazione del torrente Lentro, per poi arrivare in città dopo aver superato alcuni dislivelli. La condotta doveva superare una collina alta poco più di 20 metri (circa 70 piedi) ed il raccordo con le due condotte che si trovavano ai due lati della collina era stato realizzato mediante un sifone di rame. L’acqua non passava ed anzi accadeva uno strano fenomeno: l’acqua con cui preventivamente era stato riempito il sifone, al momento del raccordo, sgorgava dal sifone alle due condotte che si trovavano ai piedi della collina finché il livello dell’acqua nei due rami del sifone non raggiungeva una quota di circa 10 metri. 

        Scriveva Baliani a Galileo (27 luglio 1630):

Abbiam fatto un sifone di rame, conforme al disegno inchiuso, ove CA è il livello: A ove

piglia l’acqua, B ove ha da uscire, C l’imbottaio per dove si empie il sifone. DE l’altezza a piombo che l’acqua ha da salire. Però questo sifone non ha l’effetto desiderato; anzi, aperto, ancorché chiuso dal di sopra, l’acqua esce da tutte le parti, e se si tien chiuso da una parte, aprendo dall’altra, ad ogni modo da questa esce l’acqua. Io non mi posso dar a credere che l’acqua habbia in questa occasione voluto appartarsi dalle sue proprietà naturali, onde è forza che, uscendo 1’acqua, vi sottentri aria nella parte di sopra: però non si vede di dove.
Avviene un’ altra cosa che mi fa stupire; et è, che aprendosi la bocca A, esce l’acqua sin che dalla parte D sia scesa per la metà in circa [arrivando cioè a circa 10 metri di altezza, ndr], ciò è sin a F, e poi si ferma.

        Il fatto si presentava incomprensibile, e Galileo, nel rispondere a Baliani, faceva sapere che anch’egli si era imbattuto in difficoltà dello stesso genere, almeno a partire dal 1594 quando inventò un edificio da alzar acqua et adacquar terreni. Secondo Galileo (6 agosto 1630):

L’acqua si può far salire per un cannone o sifone per attrazzione e per impulso. Per attrazzione, intendo quando l’ordigno (qualunque si sia) che lavora, sarà posto nella parte superiore A del cannone AB;

per impulso, si fa montar l’acqua, tuttavolta che l’ordigno impellente sia accomodato da basso in B. Quando l’acqua si abbia a cacciar per impulso, si potrà sollevare e spignere a qualsivoglia altezza, anco di 1000 braccia [un braccio fiorentino = 0,583 m; n.d.r.], purché il cannone sia saldo e forte, siché non crepi: ma nell’alzarla per attrazzione ci e’ una determinata altezza e lunghezza di canna, oltre alla quale e’ impossibile far montare l’acqua un sol dito, anzi un sol capello; e tale altezza parrai che sia circa 40 piedi, e credo ancor meno [in realtà 32 piedi ~ 10 metri; n.d.r.].

        Ciò era anche confermato dai fontanieri di Firenze e da vari artigiani che avevano parlato della cosa con Galileo: con le pompe aspiranti non si riusciva a far salire l’acqua oltre circa 10 metri. Galileo ne aveva tentato una spiegazione (errata)della quale discuteva con Baliani nella lettera in oggetto. Secondo il nostro occorreva sostituire la vecchia teoria dell’ horror vacui (secondo la quale la Natura ha paura del vuoto e se, casualmente, si producesse un vuoto in qualche luogo, la natura stessa provvederebbe immediatamente a riempirlo di materia, e con la quale, in accordo con la fisica aristotelica, si spiegavano, all’epoca, una gran varietà di fenomeni, come il funzionamento delle ventose, delle pipette e degli stessi sifoni) con una teoria della «forza del vuoto». Galileo assimilava una colonna d’acqua ad una corda di nave, o ad una corda d’acciaio o di rame o di qualsivoglia materiale. Quando una corda di un tal genere viene tirata, ad un certo punto si rompe. Ebbene, perché non dovrebbe accadere la medesima cosa per l’acqua che viene «tirata» in un tubo ? Scriveva Galileo a Baliani ancora nella medesima lettera:

Io non havea fatto la distintione che sia diverso il far ‘salire l’acqua in un cannone per attrazzione o per impulso; e come che e da Vitruvio c da Frontino si vede che per impulso i Romani facevan salire l’ acqua in grande altezza, mentre che col sifone traversavan le valli, che mi persuado che non fussero così poco profonde, io mi dava ad intendere che lo stesso dovesse avvenire per attrazzione, e che perciò poco importasse che ‘l sifone fusse rivolto all’ ingiù overo all’ insù, ma che il sifone dovesse sempre far la sua operatione, pur che fusse fatto in modo che, non facendola, havesse a rimanervi necessariamente luogo vacuo. Conosco che io ho fatto errore, e che è verissima la consideratione di V. S., che un canape, ancor che sia d’acciaio e di qualsisia grossezza determinata, non può reger un peso immenso, e neanche se stesso, quando che sia tanto longo che ‘l suo peso sia immenso, e che perciò si regerà solo mentre che sia di una tale longhezza, la quale non si può passare, e che V. S. dichiara benissimo quanta sia questa longhezza; e mi è avviso che lo stesso debba avvenire al canale pieno d’acqua. Però so che V. S. mi permetterà che io le dica che mi resta tuttavia un dubbio, che pur V. S. accenna mentre che dice che la corda dell’ acqua si strapparà più facilmente del canape, quanto le parti dell’ acqua, nel separarsi l’una dall’ altra, non hanno da superar altra resistenza che quella del vacuo, la quale non si è sin hora determinato quanta ella sia; e se ben tanto o quanto il vacuo impedisce lo strapparsi il canape, e tanto più la corda d’acciaio, ad ogni modo mi par pure che vi sia gran diferenza, anzi che sia dubbio se possa esser che, strappandosi la corda, vi resti vacuo o no. Ma comunque ciò sia, è certo che è molto maggiore il vacuo che resta nel canale.

        In questo brano Baliani si riferiva agli acquedotti romani che aveva studiato sui testi che citava. Ne traeva l’erronea conclusione che i sifoni degli acquedotti, come quelli di figura in uso nell’antica Roma,

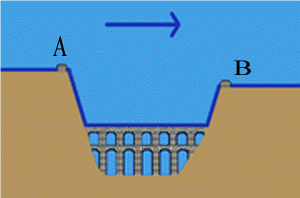
Sifone in giù.

 potevano essere invertiti a piacimento, come mostrato nella figura seguente:

Sifone in su

Ebbene, nel primo caso, l’acqua proveniente da A va, attraverso il sifone in giù, a B perché B è comunque ad un livello più basso rispetto ad A. I romani, vuoi per esperienza o per pura casualità, non realizzarono mai acquedotti in cui il livello B della figura fosse più alto di 10 metri (all’incirca) rispetto a quello A. Nel secondo caso, quello del sifone in su⁽⁷⁾, se si vuole portare l’acqua da A a C, passando attraverso il sifone, è necessario che il dislivello esistente da dove si prende l’acqua, A, fino alla massima quota a cui arriva il sifone, B, non superi quei 10 metri. Come capirà Baliani, indipendentemente da Torricelli e per altra via, è il peso dell’aria sulla superficie dell’acqua in A che permette all’acqua di salire fino ai circa 10 metri (e non oltre perché il peso dell’aria, la sua spinta, non ce la fa ad andare oltre e, se si vuole farlo, occorre aumentare la spinta dell’aria mediante pompe).

        Baliani si era scontrato con questo problema che, in precedenza non era mai stato affrontato per cercarne una soluzione che qui era indispensabile⁽⁸⁾.

Ma se si rompono corde di canapa e d’acciaio, mentre debbano reggier soverchio peso, che dubbio doviamo noi bavere che non si sia per strappare anco una corda d’acqua? anzi si strapperà questa tanto più facilmente, quanto le parti dell’acqua, nel separarsi l’una dall’altra, non hanno da superare altra resistenza che quella del vacuo succedente alla divisione; che nel ferro o altra materia solida, oltre alla resistenza del vacuo, vi è quella grandissima del tenacissimo attaccamento delle parti, del quale mancano le parti dell’acqua⁽⁹⁾.  […]

[Nel sifone di V. S.] l’acqua deve salire per attrazzione a perpendicolo sino all’ altezza di 84 palmi, per perpendicolo dico ciò essere impossibile, perché la sua corda non è sì gagliarda, ma si strappa anco in assai minor lunghezza. Né ci è di sollevamento l’essere il sifone non eretto a perpendicolo, ma inclinato, essendo che la lunghezza dell’ inclinato, et in conseguenza la quantità dell’ acqua in esso contenuta, è tanto maggiore, che ricompensa appunto la resistenza maggiore nell’ esser alzato a perpendicolo. E qui parimenti noti V. S. che l’essere i sifoni più longhi o più stretti non diversifica. nulla circa ‘1 potersi attrarre a minore o maggiore altezza; e se, vgr., in un sifone largo come una paglia, attraendo, non si può far salir l’acqua se non all’ altezza di 20 braccia, in nessun altro sifone, di qual si voglia larghezza, si farà montare ad altra altezza: ma di tutti i sifoni ~ determinata la lunghezza medesima, possibile per l’ attrazzione; perchè delle corde (per così dire) d’acqua tanto crescie la robustezza, cioè la loro grossezza, quanto il peso da reggersi, cioè la quantità dell’acqua.

        Baliani non si convinse di questa spiegazione. Egli aveva già elaborato un tentativo di teoria che, pur non respingendo l’ipotesi di esistenza del vuoto, si rifaceva alla pesantezza dell’aria. Di quest’ultimo argomento Baliani e Galileo si erano già scritti, come visto. Ora Baliani collegava le sue difficoltà e la non soddisfazione della spiegazione galileiana del mancato funzionamento del sifone, proprio alla pesantezza dell’aria. La sua lettera infatti così proseguiva:

Io non sono già dell’opinione volgare che non si dia vacuo … E per non mancare di dirle la mia opinione intorno a ciò, io ho creduto che naturalmente il vacuo si dia da quel tempo ch’io ritrovai che l’aria ha peso sensibile, e che V.S. m’insegnò in una sua lettera il modo di ritrovarne il peso esatto, ancorché non mi sia riuscito finora di farne esperienza.

        È evidente che qui Baliani aveva ben chiara la connessione esistente tra vuoto e pesantezza dell’aria, connessione che avrà un ruolo di primaria importanza nei lavori posteriori di Torricelli (1644). Ma Baliani andava oltre ed illustrava le sue idee nel modo seguente:

Io mi figuro adunque di essere nel fondo del mare, ove sta l’acqua profonda dieci mila piedi, e se non fosse il bisogno di rifiatare io credo che-io starei, sebbene mi sentirei più compresso e premuto da ogni parte di quel che io mi sia nel presente;  e per ciò io credo che per avventura io non potrei star nel fondo di qualsivoglia profondità d’acqua, la quale crescendo in infinito, crescerebbe, per mio avviso, proportionatamente tal compressione, in modo che le mie membra non vi potrebbon resistere. Ma per ritornare, dalla detta compressione in fuori io non sentirei altro travaglio, né sentirei maggiormente il peso dell’ acqua di quel che io mi faccia quando, entrando sotto acqua la state bagnandomi nel mare, io ho dieci piedi d’acqua sopra ‘l capo, senza che io ne senti il peso. Ma se io non fussi entro l’acqua, che mi preme da ogni parte, e che fussi non dico in vacuo, ma nell’ aria, e che dalla mia testa in su vi fusse l’acqua, all’ hora io sentirei il peso, il quale io non potrei sostenere, solo se havessi forza a lui proportionata; in modo che, ancorchè, ovonque, separando io violentemente le parti superiori dell’ acqua dalle inferiori, non vi rimanesse vacuo, ma vi subintrasse aria, ad ogni modo vi vorrebbe forza a separarle, però non infinita, ma determinata, e via via maggiore secondo che la profondità dell’acqua, sotto la quale io fussi, fusse maggiore: la quale non ha dubbio che chi fusse nel fondo detto di sopra di 10 mila piedi d’acqua, stimerebbe impossibile far detta separatione con qualonque forza, come che egli mai non ne farebbe la pruova; e pur si vede che non sarebbe vero che fusse impossibile, ma che 1’impedimento gli verrebbe da non haver lui tanta forza di poter far all’ acqua una tal violenza che fusse bastante a separarla.  

        Secondo Baliani dunque quando una persona si mette in acqua a poca profondità non avverte il suo peso perché è premuto da ogni parte ma se stesse in aria e quell’acqua l’avesse sulla testa se ne accorgerebbe perché il peso sarebbe grande. Allo stesso modo nell’aria noi siamo premuti da ogni parte e non avvertiamo il suo peso che invece c’è e preme dappertutto.

Lo stesso mi è d’avviso che ci avvenga nell’aria, che siamo nel fondo della sua immensità, e non sentiamo né il suo peso, né la compressione che ci fa d’ ogni parte … Ma se fossimo nel vacuo allora si sentirebbe il peso dell’aria che abbiamo sopra il capo, il quale io credo grandissimo, perché, ancorché io stimi che quanto l’aria è più alta, sia sempre più leggera, io credo che sia tanta la sua immensità che, per poco che sia il suo peso, conviene che si sentisse quel di tutta l’aria, che ci sta sopra, peso molto grande, ma non infinito, e perciò determinato, e che con forza a lui proporzionata si possa superare, e perciò causarsi il vacuo. Chi volesse trovar questa proporzione converrebbe che si sapesse l’altezza dell’aria e il suo peso in qualunque altezza. Ma comunque sia, io veramente lo giudicavo tale che per causar vacuo, io credeva che si richiedesse maggior violenza di quella che può far l’acqua nel canale non più lungo di 80 piedi.

        Non più quindi la forza del vuoto ma la pesantezza dell’aria è all’origine delle difficoltà incontrate nella posa del sifone.

        E’ l’aria che preme in basso che permette che l’acqua salga ad una determinata altezza. Baliani si stupisce solo del fatto che l’effetto riscontrato risulti inferiore a quello previsto.

        La cosa non ebbe più un seguito immediato ma certamente Galileo dovette riflettere su quanto gli era stato riferito da Baliani e dovette certamente parlarne con Torricelli quando quest’ultimo, nel 1641, era andato a visitare il suo maestro nel domicilio coatto di Arcetri⁽¹⁰⁾ per poi restare con lui fino alla sua morte. Ma questa è un’altra storia. Baliani invece aveva risolto il suo problema pratico anche se la soluzione rendeva tutto molto complicato nella realizzazione dell’acquedotto perché o il sifone non superava quei 10 metri o occorrevano delle pompe.

A MARGINE DEL DE MOTU NATURALI GRAVIUM SOLIDORUM ET LIQUIDORUM. LA CORRISPONDENZA CON GALILEO

        Dopo un lungo periodo del quale si sa poco e nulla di Baliani, a parte una sua lettera a Galileo del 23 aprile 1632 in cui lo ringraziava per aver ricevuto il suo Dialogo sui massimi sistemi, rispetto ad alcuni passi del quale sollevava dei quesiti sui quali tornerò più oltre, nel 1638 pubblicò un  lavoro, il De motu naturali gravium solidorum, che, completamente rifatto ed ampliato in una seconda edizione del 1646 (al titolo sarà aggiunta la parola et liquidorum), darà un contributo scientifico notevole ed avrà vasta risonanza. Dell’evento Baliani informò Galileo con una lettera del 15 dicembre 1638 in cui, allegandola, affermava di essersi rifatto ai suoi insegnamenti (le sue pedate) per elaborare i suoi scritti.

        Il lavoro si occupava del moto e quindi anche della caduta dei gravi sia liberamente che su piani inclinati. Nella discussione dei problemi che si trovano nel libro avrà spazio un grande contributo di Baliani relativo alla prima comprensione della differenza tra la massa ed il peso. Inoltre risulteranno trattate altre diverse questioni tra cui le maree.

        Prima di entrare in un qualche dettaglio occorre render conto dell’accoglienza del lavoro che vedeva la luce qualche mese prima che dall’Olanda arrivassero le copie stampate dei Discorsi e dimostrazioni matematiche intorno a due nuove  scienze di Galileo. Oltre a questa coincidenza vi era quella dell’argomento trattato che riguardava nei due casi la caduta dei gravi (anche se i Discorsi di Galileo avevano una portata estremamente più vasta per gli argomenti trattati). Queste circostanze crearono una situazione di critica nei riguardi di Baliani che sembrava non aver riconosciuto pienamente tutto il suo debito verso Galileo uscendo con un lavoro simile e senza dare a Galileo i meriti che aveva. Su questo evento si intrecciarono vari commenti in differenti corrispondenze. Nell’aprile del 1639 Bonaventura Cavalieri, l’amico e corrispondente di Galileo, scriveva al filosofo e matematico Giannantonio Rocca (1607-1656), anch’egli corrispondente di Galileo: …. Quanto al libro o Dialoghi del moto del Sig. Galileo, non l’ ho ancora visto: dicono che se ne vendino in Roma, ed alcuni amici miei in Milano l’ hanno fatto venire da Parigi.
Ho ricevuto poco fa un’operetta di un Sig. Gio. Battista Baliani Genovese, intitolata De motu ‘naturali gravium solidorum, dove vi sono molte cose, credo io, inventate dal Sig. Galileo e che si vedranno in quest’ ultimo Dialogo. Io non l’ ho ancora visto con diligenza, ma nelle supposizioni che fa pare che vi sia in una parte qualche difficoltà a concederle. Lui le suppone provate da Simone Stevinio e dal Sig. Galileo. …. E Cavalieri si suppone abbia detto qualcosa anche allo stesso Baliani se quest’ultimo gli scriveva le cose seguenti: Il Galilei non mi ha somministrato sussidio a ciò, perché io non haveva notitia alcuna di quel che poi ho veduto alla propositione seconda del terzo dialogo, dopo che esso mi favorì ultimamente di mandarlomi. Ma Cavalieri non cambiò idea tornando più oltre sulle cose che non gli funzionavano nel trattatello di Baliani.

        Inizierà a questo punto un nuovo scambio epistolare tra Baliani e Galileo al quale accennerò e che però sopravveniva in epoca di gravi difficoltà fisiche di Galileo al domicilio coatto. Baliani comunque, dopo le reazioni al suo primo lavoro, lo riscrisse in modo differente. Il testo pubblicato nel 1646, quando già Galileo era morto (1642) da tempo, era molto più ambizioso di quello del 1638. Quest’ultimo era solo il primo dei sei capitoli che conteneva quello del 1646, i primi tre dedicati ancora alla caduta dei gravi ma ora anche all’impeto, al principio d’inerzia, al moto dei proiettili, alla percossa (quindi molto più vicino, almeno negli argomenti, ai Discorsi di Galileo) e gli altri tre alla caduta dei liquidi.

        L’opera di Baliani del 1646 era ora chiaramente non riportabile a Galileo, si muoveva su cammini differenti, utilizzava dimostrazioni differenti e, a volte, addirittura antagoniste a quelle di Galileo. Si può comunque dire che, visti i circa 8 anni passati dal lavoro sia di Baliani che di Galileo, anni di intensissima attività su questi problemi in tutta Europa⁽¹¹⁾, l’opera di Baliani nasceva in un’epoca più matura e poteva essere considerata complementare a quella di Galileo nelle parti dove questa risultava poco chiara, carente o troppo prolissa. La curatrice del lavoro di Baliani per Giunti, Giovanna Baroncelli, riassume la critica più accreditata a questa seconda edizione dell’opera di Baliani. In tale critica vengono messe in risalto le differenze epistemologiche e la sostanziale differenza tra le concezioni di Galileo e Baliani, “la complementarietà tra il richiamo critico all’esperienza mosso ripetutamente dal Baliani nei confronti degli enunciati galileiani e la coerenza teorica ed epistemologica contrapposta da Galileo allo sperimentalismo accentuato e non sempre sorvegliato dello scienziato genovese”. Oltre a ciò viene messo in risalto che, ingiustamente, l’intera seconda edizione di Baliani viene giudicata appiattendola sull’infelice formulazione, che qui Baliani dette, della legge di caduta dei gravi. Ma la Baroncelli ci racconta altro su Baliani ed i suoi rapporti con i perfidi gesuiti, nemici per la pelle di Galileo. Scrive la nostra critica: “Negli anni ’40 i circoli dei gesuiti italiani cercarono di ottenere l’appoggio di Baliani nell’allora rovente polemica sollevata dall’esperimento torricelliano [l’esistenza del vuoto, provata da Torricelli, era un colpo mortale all’intera fisica di Aristotele e, come vedremo, Baliani insisterà molto con Galileo per negarlo, ndr]. La cooptazione del Baliani, autorevole scienziato, uomo vicino al circolo galileiano e al tempo stesso indipendente da ogni condizionamento di scuola, avrebbe fornito un punto di riferimento scientifico autorevole e imparziale, un appoggio solido e al tempo stesso duttile, non troppo ingombrante e perciò relativamente manovrabile nel dibattito in corso sull’esistenza del vuoto; avrebbe inoltre favorito il dirimersi scientifico della controversia e di conseguenza allontanato la tentazione, temuta dall’ala più aperta dell’ordine, alla rigida chiusura dottrinale e alla limitazione del dibattito scientifico che andava sempre più insistentemente emergendo. Se in quel caso l’operazione non riuscì, andò tuttavia a segno un secondo, contrapposto tentativo. Paolo Galluzzi ha dimostrato che negli stessi anni era sorto un secondo ‘caso Galileo’, occasionato dalla saldatura evidenziata da Gassendi nel De motu impresso a motore traslato tra copernicanesimo, cinematica galileiaana e atomismo. La pericolosità della connessione innescò un nutrito e ben orchestrato coro di reazioni che coinvolse negli anni’ 40 numerosi gesuiti italiani e oltramontani (Cabeo, Morin, Le Cazre, Fabri) attorno alla solidità delle leggi enunciate nei Discorsi. Si trattò di una vera e propria seconda affaire Galilée, più sottile e subdola, che non mancò tuttavia, nelle sue punte più violente, di ammonire minacciosamente la comunità scientifica, mettendola in guardia contro il pericolo di eresia insito nell’atomismo e nella riduzione di ogni qualità a moto locale. In questo nuovo ‘caso Galileo’, a cui non fu estraneo Marin Mersenne, il Baliani ebbe una parte non secondaria, operando di concerto con il gesuita lionese Fabri, questa volta aderendo, con la seconda edizione del De motu, all’esplicito disegno di quanti volevano ribadire l’assurdità della cosmologia copernicana dimostrando la manchevolezza dell’intera teoria galileiana de motu. 

        Le indicazioni fin qui emerse invitano per il loro grande interesse ad una riconsiderazione attenta dell’origine, della composizione, stratificazione e continuo aggiustamento dei due testi de motu, le cui tracce possono essere seguite, in parte, proprio nel carteggio Baliani-Galileo, negli scambi epistolari con l’ambiente galileiano (Cavalieri, Castelli, Rocca) e con i circoli scientifici francesi facenti capo a Mersenne, nonché con la varia ed eclettica cerchia degli scienziati gesuiti italiani e oltramontani (Confalonieri, Grassi, Fabri)”.

        Noi abbiamo seguito il carteggio con Galileo fino alla comunicazione che Baliani faceva nel dicembre 1638 della pubblicazione della prima edizione del suo De motu. Vediamo ora cosa accadde a partire da questo momento, da quando Galileo, ormai non più in grado di leggere, ricevette la lettera di Baliani del dicembre 1638 e, il 7 gennaio 1639, rispondeva. La lettera di Galileo iniziava con il racconto a Baliani dei suoi malanni e con i complimenti per il suo lavoro:

La gratissima lettera di V. S. Ill.ma mi fu resa hieri, insieme col suo libro Del moto, dal molto Rev. P. D. Clemente di S. Carlo delle Scole Pie, compagno del Rev. P. Francesco di S. Giuseppe: e perchè il mio infortunio di esser cieco del tutto da circa due anni in qua non mi permette il poter vedere né anche il sole, non che oggetti tanto minori e privi di luce quali sono le scritture e le figure geometriche, ho ottenuto questo giorno che il sopradetto P. D. Clemente sia venuto a trattenersi da me per molte hore, nel qual tempo haviamo di compagnia scorso il detto suo libro, veramente con mio gusto particolare, ancorché io non habbia potuto intendere distintamente le dimostrationi, non potendo incontrarle con le figure; ma per la pratica che ho della materia, e per sentire buona parte delle sue propositioni incontrarsi con le mie già scritte, ho penetrato i suoi sensi e concetti.

Quindi Galileo passava ad illustrare i suoi Discorsi confrontandoli, in linea di massima, con il De motu di Baliani che, egli si lamentava, ancora non aveva avuto neppure in una sola copia:

Io ho trattato la medesima materia, ma alquanto più diffusamente e con aggressione diversa; imperoché io non suppongo cosa nessuna se non la diffinitione del moto, del quale io voglio trattare e dimostrarne gl’accidenti, imitando in questo Archimede […]. lo mi dichiaro di volere esaminare quali siano i sintomi che accaggiono nel moto di un mobile il quale, partendosi dallo stato di quiete, vada movendosi con velocità crescente sempre nel medesimo modo, cioè che gl’ acquisti di essa velocità vadano crescendo non a salti, ma equabilmente secondo il crescimento del tempo; siché il grado di velocità acquistato, per esempio, in due minuti di tempo sia doppio dell’ acquistato in un minuto, e l’acquistato in tre minuti, e poi in quattro, triplo, e poi quadruplo, del medesimo che fu acquistato nel primo minuto; e non premettendo altra cosa nessuna, vengo alla prima dimostratione, nella quale provo, gli spatii passati da cotal mobile, essere in dupplicata proportione di quella de’ tempi, e sèguito poi a dimostrare buon numero di altri accidenti. De’ quali ella ne tocca alcuni, ma io molti più ve ne aggiungo, e per avventura più pellegrini, come V. S. Ill.ma potrà vedere nel mio Dialogo di tal materia, già due anni fa stampato in Amsterdam: del quale non me ne è venuto, salvo che di foglio in foglio mandato di là per le correttioni e per fabbricarne una tavola delle cose più notabili; di poi non me ne è pervenuto pur uno, e tuttavia so che ne sono stati sparsi per tutte le provincie settentrionali, e, quello che è più, intendo che in Roma ve ne sono capitati e che vi si vendono tre scudi l’uno; e questi per avventura possono essere quegli che, essendo pervenuti in Praga, furono immediatamente raccolti tutti da’ PP. Gesuiti, sicché né l’Imperatore istesso potette ottenerne una copia, havendo mandato il S.r Francesco Piccolomini, suo cameriere per haverle, come l’istesso S.r Piccolomini, tornato qua circa due mesi sono, a bocca mi replicò. Se mai me ne perverranno, non mancherò di inviarne uno a V. S. Ill.ma; intanto starò aspettando con desiderio di sentire i suoi pensieri intorno alli liquidi, alla mia mente molto oscura e piena di difficultà.

Galileo continuava parlando un poco del suo metodo, del suo lavorare in vari casi per ipotesi (argomento ex suppositione sopra il moto, in quella maniera diffinito) guidato sempre da Archimede. Comunicava infine a Baliani il seguito del suo lavoro e cioè la trattazione del moto dei proiettili, della forza della percossa, della resistenza dei materiali. A questo punto devono esservi state altre lettere tra i due che non possediamo. La prima lettera, successiva a quella vista, della quale disponiamo è una lettera di Baliani a Galileo del 1° luglio 1639 nella quale Galileo veniva ringraziato per avergli inviato il 20 giugno un libro de’ Movimenti locali [i Discorsi] che aveva letto con grandissimo gusto anche perché, per quanto avesse cercato in Europa, non era riuscito ancora a procurarsi una copia di tale lavoro. Baliani passava quindi a commentare ciò che aveva letto confrontandolo con il proprio metodo d’indagine che considera diverso da quello di Galileo che viene accusato di non far dipendere le sue conclusioni da esperienze:

Ringratio V. S. parimente della pacienza havuta in legger le mie cose e delle considerationi che vi fa. Io in vero ho giudicato che l’esperienze si debbano por per principii delle scienze, quando son sicure, e che dalle cose note per lo senso sia parte della scienza condurci in cognitione delle igniote. Non ricuso però in questo ciò che V. S. mi promette di questo particolare trattarmene un’altra volta, come anche io penso di raggionarne compitamente in un trattatello che col tempo penso di publicare in materia di loica, e mostrare come la scienza non opera altro in noi, e che il cercar le cause spetta ad un altro habito, detto sapienza, come ho accennato nella prefattione del libro de’ Moti, e sì come i principii delle scienze sogliano essere deffinitioni, assiomi e petitioni, che queste nelle cose naturali siano per lo più esperienze, e sopra tali son fondate l’astronomia, la musica, la meccanica, la prospetiva e tutte le altre.

Vi è una troppo grande valutazione dell’esperienza che tende a far sparire, almeno in questo modo di affrontare il problema, il ruolo dell’elaborazione teorica ed anche della possibilità di avanzare teorie anche se non immediatamente confortate dall’esperienza perché, a volte, l’esperienza non è realizzabile per mancanza di strumenti tecnici. Ma vi era anche un altro sottile motivo che spingeva Baliani a criticare la ricerca delle cause che iniziava a muovere Galileo. La questione si legava ancora ad Aristotele che vedeva nella ricerca delle cause un ambito estraneo alla fisica e quindi attinente alla metafisica. La stessa matematica che è in qualche modo fuori dall’esperienza veniva messa in discussione. Il fatto straordinario è che l’accusa di non operare adeguatamente con esperienze viene fatta a Galileo il quale, deve sempre essere tenuto presente con una adeguata storicizzazione delle questioni, era un apripista che aveva oltre al compito di rompere una gran quantità di pregiudizi, di impedimenti, ed addirittura un intero apparato culturale solidamente sedimentato in secoli. Ciò lo obbligava a fare varie cose che non soddisfacevano i puristi del cambiamento, come lo scrivere in volgare e parlare in modo discorsivo. Se si confrontano i testi di Torricelli e dello stesso Baliani, per fare solo due nomi, si trovano una serie di teoremi con relative dimostrazioni che fanno felici gli addetti ai lavori ma non comunicano nulla a chi deve entrare in questo nuovo mondo che utilizza non solo argomenti ma anche una logica differente. E’ facile dopo che Galileo ha fatto il grosso, per il quale si trovava arrestato ad Arcetri, dire che le cose non sono soddisfacenti perché vi sono poche dimostrazioni, poca matematica, e poche esperienze raccontate. Comunque Baliani diceva chiaramente ciò che pensava.

        La lettera proseguiva con un paio di osservazioni abbastanza acide relative a ciò che Baliani non aveva trovato nei Discorsi. Aspettava di togliersi delle curiosità su cose lette nel Dialogo che sperava ora approfondite, in particolare voleva sapere come aveva fatto a contare i cinque secondi per un oggetto che cada da un’altezza di cento braccia.

Rispetto a quel che dice di haver scritto delle vibrationi del pendolo fatto nell’istesso tempo, e dell’osservatione de’ gravi che con pari velocità discendono, io non ho veduto altro, solo quel che scrive ne i Dialoghi del Sistema [il Dialogo sui Massimi sistemi, ndr]. Anzi che in quelli V. S. dice qualche cosa, di che io sperava che ne dovesse dar più distinto conto in questi, cioè di haver osservato che il grave discende di moto naturale per cento braccia in cinque minuti secondi d’ hora; sperava, dico, che dovesse dir con che ragione si è assicurata che sian cinque secondi, e massime V. S. dà conto distinto di altre esperienze fatte in simil materia.

        Subito dopo Baliani entrava in critiche particolari e  dettagliate  su  vari  argomenti che aveva trovato nei Discorsi⁽¹²⁾:

E finalmente, perché V. S. mi scrive che io le dica liberamente il mio senso, io le dico sicuramente che tutto ciò che ho detto di sopra non stimo che vi sia ponto di adulatione, perchè V. S. insegna al mondo molte cose nuove e bellissime, mostrando in che consiste che le machine picole non riescono in grande, e lo prova benissimo particolarmente all’ottava propositione del secondo Dialogo, alla quale io arrivai con grandissimo gusto. Mi par benissimo provato ove consista non solo la resistenza al rompersi delle corde, legne, pietre e metalli, ma anche dell’acqua, se ben di questa già V. S. me ne fece parte altre volte con sua lettera, in occasione che io le domandai aiuto in un siffone alto circa 40 braccia⁽¹³⁾, che non riuscì: e tutti i discorsi in tal materia, che V. S. fa delle particelle di vacuo, ancorché io non ne sia totalmente sodisfatto, ad ogni modo le conosco per cose sotilissime e verissime, servendosi di propositioni di mattematica molto sottili e molto a proposito […]. Tali anche harei stimato ove ritrova la proportione fra l’acqua c l’aria, se non fusse che non mi è comparsa per nuova, perciò che V. S. con sua lettera altre volte me ne fece parte. Tutto il discorso del secondo Dialogo [è la Giornata Seconda dei Discorsi, quella che tratta di resistenza dei materiali, ndr] è parimente molto dotto, né io vi ho difficultà di consideratione: solo desiderei che V. S. havesse un tantino più dichiarato alla propositione prima, che il momento della forza in C al momento della resistenza è come e D alla metà di DA⁽¹⁴⁾; ….

        Seguono alcune puntuali obiezioni o perché Galileo è stato troppo sintetico o perché non è credibile che un’esperienza dia tali risultati o cose simili (vedo che V. S. ha saputo cacciarne molte conchiusioni, che non ho ritrovato io). Una osservazione era relativa ai vuoti disseminati che Galileo aveva supposto per rendere conto della condensazione e rarefazione ed al fatto che Galileo introduceva  a proposito della dimensione dei supposti vuoti considerazioni sugli indivisibili, argomento che aveva sviluppato, da un punto di vista matematico, per anni con Bonaventura Cavalieri. Scriveva il nostro:

tutti i discorsi in tal materia, che V. S. fa delle particelle di vacuo, ancorchè io non ne sia totalmente sodisfatto, ad ogni modo le conosco per cose sotilissime e verissime, servendosi di propositioni di mattematica molto sottili e molto a proposito.

Altra osservazione riguarda la discussione che Galileo aveva fatto della traiettoria di un proiettile di archibugio. La strana posizione di Baliani prevedeva il semplice non credere che accadesse quanto Galileo affermava:

Da ciò che discorre […] par che, sparandosi in alto un’archibugiata, dovrebbe la palla far l’istessa passata, in distanza, verbi gr., di 10 palmi dall’archibugio, tanto nello scendere quanto nel salire; il che né credo che riuscirebbe in fatto, né pare che si possa sciorer per lo condensamento dell’aria, perciò che non è questa, per mio aviso, tale altezza che nello scendere il grave non osservasse la regola della duplicata proportione in tempi uguali.

In definitiva si tratta di osservazioni marginali. La conclusione di Baliani è la seguente:

Io vedo che l’ harò attediata, ma più mi converebbe attediarla se io volessi lodar, cosa per cosa, tutto ciò che per mio parere è degno di tal lode; perciò farò fine, con bacciar a V. S. le mani e con restar desideroso di ricever suoi commandamenti, e pregarle dal Signore vista, salute et ogni maggior prosperità.

        Rispondeva Galileo il 1° agosto 1639 con una lunga lettera iniziando da quel grave che cade da 100 braccia in 5 secondi. Il discorso di Galileo è quello di uno scienziato che parla ad un tecnico pedante. Le esperienze in fisica devono poter fornire legge generali. Non si può fare una esperienza per un oggetto in caduta da 100 braccia e poi da 110 braccia e poi da 200 braccia e poi dal numero di braccia a piacere. Occorre fare un certo numero di esperienze, ricavare una legge che poi deve essere valida per qualunque situazione. Non è pensabile che ogni caso che differisca di un poco da quello sperimentato debba prevedere una nuova esperienza. Sarebbe la paralisi e la condanna della fisica all’inutilità. Quanto ho ora detto, lo diceva Galileo nel modo didascalico seguente, mostrando un qualche fastidio:

V. S. Ill.ma mi dice che volentieri harebbe sentito 1’artificio col quale io mi sia potuto assicurare che il grave descendente a perpendicolo, partitosi dalla quiete, passi cento braccia di altezza in cinque minuti secondi. Qui due cose si cercano: la prima è il tempo della scesa per le cento braccia, la seconda è il trovare qual parte sia questo tempo delle 24 hore del primo mobile. Quanto alla prima operatione, la scesa di quella palla che io fo scendere per quel canale ad arbitrio nostro inclinato, ci darà tutti i tempi non solo delle cento braccia, ma di qualsivoglia altra quantità di caduta perpendicolare, atteso che, come ella medesima sa e dimostra, la lunghezza del detto canale, o vogliamo dire piano inclinato, è media proporzionale tra la perpendicolare elevatione di detto piano e la lunghezza di tutto lo spazio perpendicolare che nel medesimo tempo si passerebbe dal mobile cadente: come, per esempio, posto che il detto canale sia lungo 12 braccia, e la sua perpendicolare elevazione sia mezo braccio, un braccio o due, lo spazio passato nella perpendicolare sarà braccia 288, 144 o 72, come è manifesto. Resta hora che troviamo la quantità del tempo delle scese per il canale. Ciò otterremo dalla ammirabile proprietà del pendolo, che è di fare tutte le sue vibrationi, grandi o piccole, sotto tempi eguali. Si ricerca, pro una vice tantum, che dua, tre o quattro amici curiosi e pazienti, havendo appostata una stella fissa che risponda contro a qualche segno stabile, preso un pendolo di qualsivoglia lunghezza, si vadano numerando le sue vibrationi per tutto il tempo del ritorno della medesima fissa al primo luogo; e questo sarà il numero delle vibrationi di 24 hore. Dal numero di queste potremo ritrovare il numero delle vibrationi di qualsivoglino altri pendoli minori e minori a nostro piacimento; siché se, vgr.[è l’abbreviazione di ‘verbi gratia’ ed equivale al nostro ‘per esempio’, ndr], le numerate da noi nelle 24 hore fossero state, vgr., 234 567, pigliando un altro pendolo più breve, col quale uno numeri, per esempio, 800 vibrationi mentre che l’altro numerasse 150 delle maggiori, già havremo per la regola aurea il numero delle vibrationi di tutto il tempo delle 24 hore: e se con queste vibrationi vorremo sapere il tempo della scesa per il canale, potremo con la medesima agevolezza ritrovare non solo i minuti primi, secondi e terzi, ma quarti e quinti, e quanto più ci piacerà. Vero è che noi potremo passare a più esatte misure con havere veduto et osservato qual sia il flusso dell’ acqua per un sottile cannello, perchè raccogliendola, et havendo pesata quanta ne passa, vgr., in un minuto, potremo poi, col pesare la passata nel tempo della scesa per il canale, trovare l’esattissima misura e quantità di esso tempo, servendoci massime di una bilancia così esatta che tira ad un sessantesimo di grano. Questo è quanto all’ artificio; il quale penso che ella stimerà esquisitissimo, ancorché poi volendo sperimentare se quello che io scrissi delle 100 braccia in cinque secondi sia vero, lo trovasse falso, perchè per manifestare la estrema gofferia di quello che scriveva et assegnava il tempo della caduta della palla d’artiglieria dall’ orbe lunare, poco importa che i cinque minuti delle 100 braccia siano o non siano giusti.

        Galileo passava quindi all’osservazione di Baliani sui supposti vuoti per rendere conto della condensazione e rarefazione, fornendo un’altra lezione al fisico genovese: a volte è necessario avanzare delle teorie che ci forniscano modelli di comportamento delle cose che studiamo restando comunque pronti ad abbandonarli quando ne verifichiamo in ulteriori prove o speculazioni la fallacia:

Che V. S. Illustrissima, benché approvi quelle sottigliezze che io arreco, in proposito di quei vacui disseminati, per la esplicatione della condensatione e rarefatione senza la necessità di introdurre la penetratione dei corpi o gli spatii quanti vacui, soggiunga poi di non restare intieramente appagato, io non me ne maraviglio, dovendo noi con l’intelletto fare una mescolanza di infiniti e di indivisibili, quelli per la troppa grandezza, e questi per la piccolezza, soverchiamente sproportionati all’ intelletto nostro, terminato e finito: e bene a me sarebbe carissimo il sentire qualche sua contemplatione in proposito di questi due effetti, ché sono sicuro che sentirei concetti molto più rationabili di quelli che sono stati sin qui arrecati da gl’ altri filosofi.

La successiva risposta di Galileo riguardava l’insoddisfazione di Baliani relativa alla propositione prima della Giornata seconda dei Discorsi, dove Galileo, secondo Baliani, avrebbe dovuto dire che il momento della forza in C al momento della resistenza è come e D alla metà di DA (si riveda in proposito la nota 14). Scriveva Galileo:

Quanto al desiderare che ella fa di essere assicurata che nella mia propositione prima del secondo Dialogo la forza della resistenza habbia la medesima proportione che CB alla metà di BA, mi pareva che fusse assai chiaro, mentre che si parla di prismi o di cilindri, intorno al centro de’ quali siano circunfuse resistenze di eguali momenti: nella quale operatione casca il medesimo accidente che interviene nel vette AB, il cui sostegno sia in C, dove posti nella

               B___________|____________________________A
                                    C

minore distanza CB quantisivogliano pesi eguali, pendenti da distanze eguali, faranno la medesima resistenza alla forza posta in A, che se tutti i detti pesi, ridotti in un solo, pendessero dal mezo di BC. E quando sopra di ciò gli restasse pure qualche dubbio (il che non credo), tenterò con più distinta dimostratione di rimoverlo.

Riguardo all’altra questione posta da Baliani, quella relativa all’elevazione  e quindi ricaduta del proiettile di archibugio, Galileo, ancora con grande pazienza, spiegava:

Che poi l’impeto della palla descendente dalla altezza dove dalla forza del fuoco fu cacciata, non racquisti, tornando indietro, giunta le dieci braccia vicina all’archibugio, che ella ebbe quando da principio fu scaricata, da me è tenuto per effetto verissimo; ma questo non altera punto la mia propositione, nella quale io dico che il grave descendente da alto racquista, nei medesimi luoghi della scesa, della forza che era bastante a rispingerlo in su, quando ne’ medesimi luoghi si ritrovò salendo. Ma questo effetto niente deroga dalla mia prima opinione e proposta, e forse da quello che già si legge nei luoghi da lei citati raccor si potrebbe; ma è vero che, senza aggiungere io alcune nuove osservationi, forse non potrebbe agevolmente esser compreso. Ma il produrle ricerca un poco più di ozio e di quiete di mente di quella che di presente io posseggo: lo farò altra volta, quando ella pure me lo richiegga.

        La lettera si avviava alla conclusione e Galileo poteva ammettere che qualcosa non era certamente spiegata come egli avrebbe voluto. Accettava una obiezione di Baliani dicendo però che anche egli aveva usato la stessa proposizione alla quale faceva obiezione:

Che poi il principio che io suppongo […] non gli paia di quella evidenza che si ricercherebbe ne’ principii da supporsi come noti, gli lo voglio concedere per hora, ancorché ella medesima faccia l’istessa suppositione, cioè che i gradi di velocità acquistati sopra l’ orizonte da’ mobili descendenti per diversi piani dalla medesima altezza siano eguali.

        La parte finale riguardava invece le gravi disfficoltà che aveva avuto Galileo nello scrivere quest’ultimo lavoro, difficoltà aggravatesi sempre più con il passare del tempo.

Hor sappia V. S. Ill.ma, che doppo haver perso la vista, e per conseguenza la facoltà di potere andare internando in più profonde propositioni e dimostrationi che non sono le ultime da me trovate e scritte, mi sono andato nelle tenebre notturne occupando intorno alle prime e più semplici propositioni, riordinandole e disponendole in miglior forma et evidenza; tra le quali mi è occorso di dimostrare il sopradetto principio nel modo che a suo tempo ella vedrà, se mi succederà di havere tanto di forze che io possa migliorare et ampliare lo scritto e publicato da me sin qui intorno al moto, con aggiungervi altre speculationcelle et in particolare quella attenente alla forza della percossa, nell’ investigatione della quale ho consumate molte centinaia e migliaia di bare, e finalmente ridottala ad assai facile esplicatione, siché altri in manco di mez’ hora di tempo potrà restarne capace. […]

        Baliani rispondeva a questa lettera il 19 agosto 1639 con uno scritto in cui continuava ad insistere sui medesimi dettagli affermando che sembrava impossibile che accadesse così e, di fatto, continuando a mettere in dubbio sia ciò che Galileo scriveva, sia facendo finta di non capire le spiegazioni di fondo che Galileo gli forniva. INoltre si diceva soddisfatto delle risposte ma proseguiva con gli stessi quesiti. Ricominciò con la questione del grave che cade da 100 braccia in 5 secondi non soddisfatto del modo per misurare il tempo, mediante un pendolo tarato sull’arco delle 24 ore, che Galileo gli aveva comunicato. Questa volta richiamava la pretesa autorità di un altro che, per somma felicità di Galileo e per rendere conto della perfidia di Baliani, era un gesuita, padre Niccolò Cabeo (1586-1650). Scriveva un qualcosa che da un punto di vista fisico è profondamente errato e cioè che la misura si deve fare con un solo determinato strumento. Affermava cioè che occorreva disporre di un pendolo che facesse l’oscillazione in un secondo in modo da poter contare con facilità i 5 secondi:

Vedo ciò che mi dice del modo di assicurarsi che il grave discenda per cento braccia in cinque secondi, il che tutto camina benissimo. Io hebbi tal pensiero per altra strada, e stimai che a questo dovesse giovare il ritrovar un pendolo di tal longhezza che facesse le’ vibrationi precisamente in un minuto secondo; e perchè è cosa che richiede diligenza e patienza, pregai il Padre Nicolò Cabeo, che mi pareva atto a ciò et a molto maggior cosa, che volesse cercarlo, et esso mi scrisse da’ Ferrara di haverlo fatto, e me ne mandò la misura, che è come questa che è qui in margine [si tratta di una semplice linea verticale lunga 22,3 centimetri con estremi E e D, ndr]: ove dice che il filo ha da esser longo quanto ED, e nel D sia il centro della palla grave da applicarvisi, dicendo che in un secondo ritorna la palla nel luogo di dove partì. Questo, come V. S. vede, serve per un horrologgio da misurar molte cose che richiedono tempo breve, e particolarmente servirebbe a questi (sic) di misurar la scesa del grave, ove fose una torre altissima.

Il solo fatto che Baliani dovesse fargli un disegno della lunghezza del pendolo che doveva essere proprio come quella disegnata, mostra quanto insensata fosse la cosa. In ogni caso, nell’ipotesi di avere un modo diverso di effettuare la misura si dice che si è soddisfatti di quanto viene detto e si dice che forse quest’altro modo potrebbe andare meglio … Ma Baliani andava sempre più sulla strada dell’indisponenza, ancora maggiore se si riflette all’età che aveva Galileo, a quante volte aveva detto che con i disegni non riusciva più a ragionare e soprattutto a sollevare questioni di tale banalità su un’opera, i Discorsi, gigantesca per respiro e contenuti. Le critiche di Baliani seguivano sempre sugli stessi argomenti ai quali Galileo aveva già risposto e così la lettera seguiva sulla vicenda dei vuoti nella materia, quelli con i quali si poteva spiegare la rarefazione e la condensazione. Baliani forniva la sua visione in un argomento che Galileo aveva ben spiegato essere una pura ipotesi. L’ipotesi di Galileo valeva quanto la sua negazione da parte di Baliani e dopo che Galileo aveva già risposto perché continuare ?

Per quello che spetta alla condensatione, intorno alla quale V. S. dice coso belissime e sottilissime, io cosi alla grossa mi andava fra me immaginando che la materia sia atta a condensarsi, e che rispetto a lei non sia absurda la penetratione, già che pare assai chiaro che debba esser più materia in un cubo di piombo che di pietra, e che per la istessa raggione ne possa esser più in un cubo di aria densa che rara, e che l’impedimento al penetrarsi sia solo fra le cose di sostanza diversa, nelle altre no; ché anche il vetro vedo che si piega, onde la superficie interna si fa minore, né io so salvarlo senza la penetratione. Et in somma la materia è cosa sicura che ha quella natura che è piacciuto a Dio di darle quando la creò, né vedo esperienze che mi assicurino che la creasse impenetrabile.

Il passaggio alla questione successiva mostra che Baliani doveva accettare quanto Galileo diceva, almeno nel caso specifico, anche se lo fa con un molesto sarcasmo:

Ciò che dice nella propositione prima del secondo Dialogo, mi parve verissimo, e tanto più mi si conferma con ciò che V. S. dice nella lettera: il poco scropolo che mi resta è solo se, per quanto sia vero, si dovessi domandarlo in una petitione.

A proposito dell’archibugio, Baliani si dava per soddisfatto ma non c’era verso che si convincesse (è proprio così !) perché in realtà egli non credeva in alcun modo alla possibilità di moto parabolico e quindi insisteva, pur affermando che non sapeva per quale ragione:

In quanto all’ impeto della palla descendente dall’altezza ove fu cacciata dal’archibuggio, non solo son sodisfatto di ciò che dice nella lettera, ma anche di quel che dice nel Dialogo, che ho letto di nuovo. Crederei però che chi havesse commodità di torre di grand’ altezza, potrcbbono farsi delle esperienze a questo proposito, e non solo vedere se la palla dell’archibuggio, il quale a questo effetto doverebbe esser molto curto, tirata perpendicolarmente all’ in giù, andasse perdendo vigore, ma se spinta da stromento di forza minore, come da una balestra, perdesse di velocità; parendomi, ma non so per che raggione, che possa essere che la perda, e poi caminando avanti, possa esser che la riacquisti, se ben, come ho detto, par che la raggione voglia il contrario.

E continua con sottigliezze che davvero devono aver messo a dura prova il vecchio e malandato Galileo, chiudendo la lettera affermando che una certa frase, quicunque gradus velocitatis sit in mobili, sua natura indelebiliter impressus etc., invece di metterla lì, Galileo avrebbe dovuto metterla all’inizio del lavoro.

        Galileo rispondeva il 1° settembre 1639 e sarà l’ultima volta che scriverà a Baliani. Le lettere di Galileo erano via via più privi di convenevoli, rispondevano all’interlocutore per pura cortesia poiché davvero non capivano il fine di tante sottiglieezze, tanto più che era diventato chiaro che dietro Baliani vi erano i gesuiti.

        Scriveva Galileo a proposito del pendolo per misurare il tempo che il Padre Cabeo poteva anche pensare di usare un pendolo qualunque utilizzando poi un pochino di matematica (che da tempo si conosce) per ricavare il tempo di un secondo:

quanto al misurare il tempo con un pendulo aggiustato a fare le sue vibrationi in un minuto secondo, si avanza la fatica del fare il calculo con la semplice operatione della regola aurea [averlo tarato sulle 24 ore, ndr], havendo una volta tanto tenuto conto del numero delle vibrationi di qualsivoglia pendolo fatte in 24 ore: la quale osservatione è necessario che il Padre Cabeo habbia fatta con un pendulo di qualsisia lunghezza, e da esso cavatane, con l’inventione delle medie, la lunghezza del pendolo di un minuto secondo; la quale inventione è sottoposta a qualche errore, il quale, benché piccolo, multiplicato secondo il numero delle molte vibrationi, può partorire notabile errore, il che non accade nelle vibrationi non obbligate alla lunghezza del filo che, molte centinaia di volte replicate, ci deve dare la misura del tempo, siché ogni piccolo errore preso nella lunghezza del pendulo va molte centinaia di volte multiplicato: mentre nell’ altra mia operazione l’errore non può nascere, salvo che nel numerare le vibrazioni, delle quali una sola parte di una sola vibratione può esser presa più o meno del giusto. Dove accade (per dichiararmi con un esempio) il medesimo che avverrebbe a quello che volesse assegnare la lunghezza dell’ anno da due ingressi del sole nell’ equinoziale, presi con l’intervallo di un solo anno tra ingresso et ingresso; dove l’errore di un quarto o di una mez’ ora casca tutto sopra la determinazione della quantità dell’anno, la qual quantità ritenuta come giusta con tale errore, volendo assegnare la quantità del tempo di cento, 200 e più anni, partorisce errore di 100 o 200 volte maggiore di quello che cadde nella determinazione di un solo anno: ma se si piglierà l’ingresso del sole nell’equinoziale accaduto et osservato 1000 o 1500 anni fa, e si prenderà simile ingresso al presente, posto che da gli antichi si fusse errato di una meza ora, e che non meno anco da noi si incorresse in simile errore, questo, compartito nelle quantità dei 1000 o 1500 anni, al più che lui possa ingannare nell’assegnare la quantità del tempo di un anno, non può partorirmi maggior errore di quello che importi la millesima parte o 1500ma di tutto l’errore intrapreso.
Che l’uso del pendolo per misuratore del tempo sia cosa esquisitissima, ho io detto molte volte; anzi ho raccolte insieme diverse operazioni astronomiche⁽¹⁵⁾, nelle quali col benefizio di tal misuratore trovo io precisioni infinitamente più esatte che quelle che si traggono da qualisivogliono strumenti astronomici, quando anco i quadranti e sestanti, armille o altri tali, havessero i lati o i diametri lunghi non 40 solo le dua o tre braccia di quelli di Ticone [Tycho, ndr], ma né 20, 30 o 50, divisi anco non solo in gradi e minuti, ma in parti di minuti ancora.
E l’ haver trovato modo di misurare esattamente il diametro di una stella, oltreché per se stessa è operazione bellissima, tanto è più da stimarsi, quanto io trovo, gli astronomi che tali grandezze hanno voluto determinare si sono ingannati non dirò di 20 o 30, ma di venti o trenta mila, per cento.

Galileo passava poi a ribadire quanto detto sulla rarefazione e condensazione, affermando di nuovo che in mancanza di sperimentazioni possibili, ognuno poteva farsi l’idea che credeva migliore:

Quanto a quello che ella mi dice della opinione sua circa alla condensazione e rarefazione, cioè che ammette la penetrazione dei corpi l’uno con l’altro, già ho io scritto (come ella può vedere) che chiunque tale operazione volesse ammettere, io gli concedo quanto li piace, non havendo io hauto. intenzione di scrivere quanto in tal proposito ho scritto se non in grazia di quelli che negano la penetrazione e gli spazii vacui potersi dare in natura.

Infine Galileo passava a rispondere punto per punto alle reiterate obiezioni  mostrandosi sempre più insofferente anche se disponibile ad inviargli ogni scritto che Baliani avesse richiesto. Per chiudere, a proposito del proiettile lanciato dall’archibugio e della teoria di Baliani, scriveva

Che una palla cacciata da grandissima altezza dall’ archibuso o dall’arco all’ingiù possa perdere del primo impeto conferitogli, credo che l’esperienza lo mostrerebbe senz’ altro, e V. S. lo concede; ma soggiugne poi, poter essere che quello che ella ha perso da principio per l’impedimento del mezo, lo possa poi per se stessa andar racquistando nel medesimo mezo. Questo veramente a me sarebbe duro a concedere, quando io non havessi esperienza o dimostrazione in contrario.

Baliani scriveva due lettere successive di risposta (9 settembre e 16 settembre 1639) ma Galileo smise, per quanto ne sappiamo, di rispondere. Riporto qualche brano delle due lettere all’unico fine di mostrare quanto petulante fosse Baliani. Continuava ad insistere su cose ampiamente dibattute e sulle quali Galileo aveva dato la sua opinione. Si poteva pensarla diversamente ma insistere così era veramente fuori luogo:

Il calcolo del Padre Cabeo credo che sia fatto al modo di V. S., ché cosi io gli suggieri’ quando esso era qui; non però tanto esattamente di numerar le vibrationi fatte in 24 hore, ma credo in una o due hore solamente in qualonque longhezza di pendolo, con farvi poi il conto per la regula aurea, come V. S. dice.
Che l’uso del pendolo possa servire a’ calcoli celesti, è cosa chiara; et io ho per fantasia di valermene un dì, se haverò otio, come anche di altri stromenti fatti senza artificio e che operino giusto, intendendo io in tal caso di valermi poco di uno sestante, che ho assai bello, di 5 piedi in circa di semediametro, fatto in Bologna di ordine del Ticcone, di cui esso fa mentione nelle sue lettere, che restò appresso al Magino [Giovanni Antonio Magini, astronomo anticopernicano, che nel 1588 fu preferito a Galileo per la cattedra di astronomia presso lo Studio di Bologna, ndr], da cui io lo hebbi poi: se ben so che V. S. in questo e ogn’ altra cosa harà inventioni più sottili e più belle delle mie.

Tornava poi sul proiettile dell’archibugio dicendosi soddisfatto però no.

Resto sodisfatto a pieno di ciò che dice della acceleratione del moto; però par dura cosa a credere che non solo il moto della palla di artellaria sia più veloce al principio di quel che possa essere, passato qualonque distanza di moto naturale, ma che anche qual si sia proietto, spinto o da braccio o da altro stromento, vada sempre crescendo di impeto ogni volta che si allontana dal proiciente, per quanto vada di moto violento e per quanto poco declini verso il centro; onde si verificherebbe il detto che il moto si va sempre celerando, non solo del moto naturale, ma del violento ancora, come V. S. prova benissimo […]: il che prima io stimavo falso, e par ad un certo modo contra il senso, parendo verisimile ché una ferita non solo fatta da una balestra o arco, ma da un sasso tirato dal braccio, sia maggiore quanto è più vicina a quel che la tira; onde quello che V. S. dice, che il crescimento della velocità non ha luogo ove si tratta de i proietti fatti dar impeto di fuoco, si verrebbe anche a verificare in quelli che son fatti da altri moventi di minor attività.

E quindi nell’ultima lettera ancora su una questione che si era dimenticato di dire nella precedente e con la comunicazione a Galileo di una correzione al suo De motu in una paginetta e mezza per un errore del ricopiatore o dello stampatore ⁽¹⁶⁾ (in realtà per aver appreso da Galileo che aveva errato):

e con occasione che mi è convenuto ristampar un foglio della mia operetta, per un errore trascorsovi per colpa parte del riccoppiatore c dello stampatore e parte mia, nella correttione degl’errori di stampa vi ho succintamente inestato la detta dimostratione.
Ho havuto per bene di darne parte a V. S. e mandarle una copia di detta mia operetta così l’acconcia, pregandola che la accia degna di star in un canto della sua libraria, con stracciar l’altra che le mandai prima, che non vorrei che vi stesse in alcun modo. Io credo che sia buona dimostratione, supposto per principio che la proportione degli spatii si compone della proportione dei tempi e delle velocità; e ne ho fatto una gionta alla dichiaratione del settimo postulato, facendola nascere dalla propositione decima quinta. Ho voluto mandargliele tale quale è, se ben con poca speranza che senza veder le figure possa dirmene intieramente il suo senso. Con questa occasione spero anche nel fin dell’opera haver dimostrato, che ove il cadente gionge e si muove sopra il piano orizonntale, fa, in tempo uguale, moto per ispatio doppio li. quel che fece cadendo tanto perpendicolarmente quanto sopra piano comonque sia inclinato.

La lettera si chiudeva con un Baliani che racconta di altre sue esperienze ma, anche qui, il tutto è marginale e privo di ogni interesse per l’interlocutore Galileo. Resta la penosa mistificazione e l’inserimento nel De motu di una cosa trovata da Galileo che Baliani spacciava come un piacevole ritrovarsi alle medesime conclusioni essendoci arrivate per vie diverse. Queste piccole bassezze, il lavorio sotterraneo insieme ai gesuiti rendono conto del perché Baliani fu trascurato anche per le cose buone che aveva fatto.

IL DE MOTU NATURALI GRAVIUM SOLIDORUM ET LIQUIDORUM (1638). IL CONTENUTO DELL’OPERA

        Una delle difficoltà più grandi che si erano avute nello spiegare il moto ed i concetti collegati, fino a circa la metà del Seicento, nasceva dalla confusione esistente tra le due grandezze massa e peso. Fu indubbiamente Baliani il primo a dire delle cose che andavano a separare i due concetti. Fermiamoci per ora su questo argomento osservando però che Baliani, nel fissare le sue osservazioni al 1611, stava dicendo che Galileo non c’era entrato nulla nelle sue elaborazioni, anche se, fino all’incirca al 1638 lo stesso Baliani si professava umile allievo di Galileo (è dal 1645 che Baliani affermerà la sua completa indipendenza da Galileo sostenendo che non avrebbe influito per nulla nei suoi lavori, tacendo di ogni trascorso epistolare). E’ interessante leggere parte dell’introduzione del lavoro di Baliani, il  De motu  (1646), per capire gli enormi passi in avanti fatti in pochi anni nella comprensione proprio del concetto di massa (quantità di materia) e del come il concetto si andava distinguendo da peso, volume e densità.

Nel 1611 … nei pochi mesi in cui, in osservanza alle leggi della mia città, ricoprivo l’incarico di prefetto della fortezza di Savona, assistendo alle esercitazioni militari compresi che le munizioni di ferro e di pietra usate nelle macchine belliche, e dunque anche tutti i corpi gravi, di specie uguale o diversa, e notevolmente diseguali in mole e gravità, percorrevano nella caduta naturale il medesimo spazio con tempo e moto uguali; ciò avveniva con straordinaria uniformità perché, ripetendo l’esperimento, constatai che due siffatti globi, entrambi di ferro, oppure l’uno di pietra e l’altro di piombo, lasciati andare nel medesimo istante da un’altezza di cinquanta piedi, giungevano al suolo in un indivisibile istante di tempo, sì che i due colpi si percepivano come uno solo, nonostante l’uno pesasse una libbra e l’altro cinquanta.
Mi ripetevo che, secondo la sentenza comunemente accolta, i gravi si muovono di moto naturale seguendo il rapporto delle loro gravità. Così decisi di mettere ulteriormente alla prova quell’enunciato, nel senso che, forse, esso descriveva correttamente la caduta di corpi aventi pressappoco la medesima mole ma peso sensibilmente diverso, ad esempio uno di piombo e l’altro di cera: sperimentai un tempo di caduta appena maggiore nel corpo di cera, ma tuttavia decisamente inferiore al rapporto delle gravità, dal momento che in una caduta di cinquanta piedi il globo di cera si trovava a distare circa un piede dal suolo nell’istante in cui quello di piombo lo colpiva, per via dell’aria interposta, ritengo, che ne ritardava il movimento ostacolandolo sensibilmente.
Decisi di approfondire l’indagine, e sospesi a cordicelle uguali sfere di materiali e gravità differenti; compresi che esse, una volta poste in movimento, si muovevano in tempi uguali, e che mantenevano tale uguaglianza tanto fedelmente che una sfera di piombo di due once, un’altra di due libbre, una di ferro di trentaquattro libbre e una di pietra di quaranta libbre, nonché un sasso informe, le cui corde di sospensione, sommate al raggio di ciascuno, fossero tra loro uguali, si muovevano in un medesimo intervallo temporale e compivano il medesimo numero di vibrazioni, indipendentemente dal maggiore o minore spazio percorso, poiché il pendolo spinto con maggior impeto percorreva sì uno spazio maggiore, ma con altrettanto maggiore velocità.
Nel corso di tali esperienze osservai con sorpresa che globi sospesi a cordicelle diseguali si muovevano di moto diseguale, e in modo tale che le lunghezze stavano tra loro come i quadrati della durata dei movimenti. Inoltre, poiché le suddette osservazioni dimostravano a sufficienza che nel moto naturale dei gravi non si conserva la proporzione – generalmente fin qui accettata – delle gravità, mi risolsi ad attribuire alla gravità il ruolo dell’agente, e alla materia o, se si preferisce, al corpo materiale, quello del paziente, e a stimare perciò che i gravi si muovano secondo la proporzione tra gravità e materia; di conseguenza, fintanto che si muovono naturalmente lungo la perpendicolare senza impedimento di sorta, si muovono ugualmente, dato che a maggior gravità corrisponde parimenti maggior materia, ovvero quantità materiale; quando invece sopravviene qualche resistenza, allora il moto è regolato dall’eccesso della virtù attiva rispetto alla resistenza passiva, ovvero agli impedimenti del moto. Questo eccesso lo chiameremo ‘momento’, e le proprietà solitamente attribuite alla gravità noi le attribuiremo al momento, asserendo che i momenti stanno tra loro nello stesso rapporto delle velocità.
Da questo principio possiamo anche dedurre la misura o proporzione con cui i gravi si muovono di moto naturale su piani comunque inclinati, una volta noti i loro corrispondenti momenti, che sembra certo debbano essere considerati maggiori o minori a seconda che i gravi poggino più o meno sopra il piano, ovvero secondo la maggiore o minore inclinazione del piano resistente; relazione, quest’ultima, che mi sembra facilmente riconducibile a quella secondo cui i momenti stanno tra loro in un rapporto reciproco di quello delle linee dei detti piani, se esse vengono tracciate a partire dal medesimo punto e fino al medesimo piano orizzontale, come affermano sia Simon Stevin nella [… Statica] sia Galileo nel manoscritto della sua Meccanica, quando descrive con grande acutezza la ‘coclea’, e come io stesso ritengo per certo, avendolo verificato con un’ esperienza analoga.

        La citazione è lunga ma era necessaria per rendersi conto come chiaramente vengono messi in gioco tutti i termini del problema in questione. E Baliani ricavava questo a partire da dati empirici che poi divengono esperienze con tutte le elaborazioni teoriche, che vengono diffusamente illustrate nelle pagine che seguono. Il tutto nasceva, come diceva lo stesso Baliani, nel 1911 quando Baliani era prefetto della rocca di Savona, quando le munizioni di cui disponeva fossero di ferro, piombo o pietra, con  mole o gravità diverse, percorrevano nella caduta spazi uguali in tempi uguali. Si vedeva facilmente che Aristotele era in errore quando affermava che la velocità degli oggetti in caduta dipende dal suo peso. E la cosa si vedeva anche con i pendoli che oscillavano sempre in modo isocrono indipendentemente dal peso che avevano sotto la fune. Al massimo si aveva una maggiore ampiezza dell’oscillazione alla quale però corrispondeva una velocità maggiore. E, partendo da questi dati sicuramente empirici, l’osservazione diventava più finalizzata con la ripetizione di eventi al fine di una loro migliore comprensione. E’ uno degli esempi più significativi della scienza galileiana che si fa strada e che fornisce agli studiosi che seguiranno, oltre alle elaborazioni, un metodo di lavoro estremamente potente ed efficace. In particolare, il fatto che il peso (gravità) si comporta come agente e la materia come paziente, sarà letteralmente ripreso da Newton allo stesso modo di virtù attiva e resistenza passiva, come vedremo (ma Newton e quasi tutti gli altri scienziati dell’epoca, tradiranno lo spirito galileiano rimettendo in ballo qua e là la metafisica. Solo Huygens, che fonda una meccanica esterna a quella newtoniana, può essere definito uno scienziato galileiano).

        Dal brano riportato si vede chiaramente che Baliani non si fermava alla distinzione tra massa (quantità di materia) e peso, ma riesce a scorgere il profondo significato del fatto che i gravi cadenti hanno tutti la stessa accelerazione: pur riferendosi solo al peso e alla massa vede già il fatto fondamentale che noi oggi esprimiamo dicendo che «la massa inerte [proprietà per cui la materia reagisce alle azioni modificatrici del suo stato di quiete o di moto uniforme e rettilineo] è proporzionale alla massa gravitazionale [proprietà per cui la materia è attratta, e attrae, altra materia]». Ma l’indagine prosegue e Baliani si chiede perché due palline uguali A e B di cui una pesa il triplo dell’altra (mettiamo A di platino, B di ferro), cadono con identica accelerazione? La risposta è semplice: per il fatto che se A è spinta con forza tripla di B, essa ha, però, anche massa tripla: è tripla la potenza di azione, ma è tripla anche la resistenza: i due fatti si compensano perfettamente. E da ciò egli ricava che:

I gravi si muovono secondo la proporzione dei loro pesi alla loro materia, onde se cadono senza impedimento, verticalmente, si devono muovere tutti con la stessa velocità, poiché quelli che hanno più peso hanno anche più materia o quantità di materia.

        E ciò vuol dire è proprio della natura dei gravi, che il loro peso è connesso alla quantità di materia, e sempre la segue, a questa condizione: tanto è il peso, cioè la sua potenza di azione, altrettanta è la materia, cioè la resistenza. E da ciò seguono effetti uguali (cioè uguali accelerazioni). Se dovessimo oggi scrivere in formula quanto Baliani sostiene dovremmo scrivere che l’accelerazione a di un grave in caduta è il rapporto tra il suo peso p e la sua massa m:
 

a = p/m      =>     p = ma

(e ciò vuol dire che di tanto cresce il peso, di tanto cresce la massa con la conseguenza che l’accelerazione, rapporto tra le prime due grandezze, si mantiene costante). E se si fa attenzione la relazione scritta non è che un caso particolare della seconda legge di Newton F = ma (che è qui solo riferito ad una particolare forza, il peso p). Nel Libro IV, infine, vi è un ribadire di nuovo il concetto precedente:

la natura dei gravi è tale che il loro peso sia connesso alla materia e sempre la segua a tale condizione: che quanto è il peso, ossia la sua potenza d’azione, altrettanta sia la materia e perciò la resistenza; dal che infine seguono effetti uguali.

        E poiché Baliani è poco conosciuto, non è male aggiungere qualcosa anche se apparentemente distante da quanto discuto. In tutto il Libro I del De motu vengono trattate tutte le possibili cadute di gravi mediante pendoli, piani inclinati e libere e non si fa mai riferimento alle diverse masse parlando genericamente solo di gravi, con ciò mostrando di aver compreso, con Galileo e come diremmo oggi, l’indipendenza della caduta di un grave dalla sua massa. Nell’introduzione al Libro III (aggiunto nel 1646) si enuncia con chiarezza il principio d’inerzia con le parole che seguono:

Poiché dunque, come si è appena detto, il mobile che è stato messo in movimento si muove in seguito uniformemente senza bisogno di alcun motore, sembra legittimo inferire che il moto produce il moto, o meglio il perseverare del moto e, per così dire, la sua stessa estensione e prolungamento, in quanto ogni volta che il mobile è stato messo in movimento diventa adatto e virtualmente capace di muoversi immediatamente nello stesso modo. Queste considerazioni mi suggerirono l’idea che l’essenza dei mobili consistesse nel comportamento indifferente nei confronti tanto della quiete quanto di qualsiasi moto, cosicché, ogni qual volta si sia dato un movimento, e da qualunque causa provenga, naturale o violenta, ad esso succeda un movimento simile, ovvero il medesimo movimento di prima perseveri con la stessa velocità che aveva assunto in un istante qualunque, fino a che non venga ostacolato. Tali riflessioni mi indussero inoltre a credere che questa prosecuzione del movimento, che scaturisce in modo così immediato dalla natura del mobile, fosse probabilmente l’unica e semplice causa dalla quale derivano tutti quegli effetti e proprietà che noi percepiamo nei fenomeni di movimento sia naturale che violento.

     Ho fin qui estratto dal lavoro di Baliani i suoi contributi più significativi ed importanti ma il De motu, anche nell’edizione del 1646, ha una quantità di problemi che conviene evidenziare per darne una visione più completa.

        I fenomeni indagati, la caduta dei gravi e l’oscillazione di pendoli, mostravano ambedue un’indipendenza dalla massa (come diremmo oggi e dico da ora per necessità discorsiva). Vi era una sorta di analogia che si estendeva anche alle leggi fino allora ricavate dei due fenomeni. Nella caduta di un grave spazi percorsi e tempi impiegati stanno tra loro nella stessa proporzione che si ha, in pendoli di lunghezza differente, tra la lunghezza del filo ed i quadrati dei periodi di oscillazione.  La cosa venne colta con chiarezza da Baliani che distinse, come visto, tra agente (la gravitas o forza attiva) e paziente (la materia o massa, che risulta un ostacolo al moto). Come scrive la Baroncelli,

“la falsa proporzionalità tra gravità e velocità poteva essere corretta a patto di sostituire alla gravità il momento, ovvero la differenza tra la forza agente e la resistenza del grave: come stanno i momenti così staranno le velocità. Di qui l’eguaglianza delle cadute libere di corpi di massa diversa, dato che ad una maggiore gravità corrisponde e fa ostacolo una altrettanto maggiore resistenza, sì da produrre un momento costante. Non solo: anche i momenti dei gravi in caduta lungo piani inclinati – concludeva con limpida sicurezza Baliani – erano esattamente calcolabili. Come avevano provato Stevin e Galileo, i momenti variano secondo l’inclinazione del piano, risultando, per un medesimo dislivello, inversamente proporzionali alle lunghezze dei piani. E poiché inoltre il momento secondo l’intendimento del Baliani è una grandezza specifica, nel senso che – come diremmo noi – non dipende dalla massa⁽¹⁷⁾, da quelli si potevano dedurre le diverse velocità di caduta lungo piani diversamente inclinati, ripristinando un fondamentale assioma metafisico, prima ancora che meccanico: l’effetto deve essere proporzionale alla causa, e perciò la velocità assunta dal mobile sul piano inclinato è direttamente proporzionale alla forza  attiva, cioè al momento.

        La proposizione XI – l’unica del breve trattato che determini qualche proprietà relativa alla velocità – stabilisce infatti, con la semplicità di un corollario, la inversa proporzionalità sul piano inclinato tra le velocità per I inclinata e per la perpendicolare e gli spazi stessi percorsi dal grave sul-1 inclinata e la perpendicolare in corrispondenza di un uguale dislivello. Essendo infatti le velocità proporzionali ai momenti, come stabilisce il secondo postulato, e questi ultimi inversamente proporzionali alle linee dei piani, segue subito l’enunciato.

        Ora, anche ammettendo che il momento a cui il Baliani pensa sia da intendersi come una grandezza indipendente dalla massa, resta da chiedersi di quale velocità egli stia qui parlando. La perpendicolare AB sta all’inclinata AC come la «velocitas super AC» sta «ad velocitatem in AB»: sembra dunque che si possa attribuire una velocità uniforme all’intero tratto AC e un’altra, maggiore ma altrettanto uniforme, allo spazio AB⁽¹⁸⁾. Ad una prima lettura si ha l’impressione che nel 1638 il Baliani sia tuttora legato all’idea che il moto di caduta avviene con velocità uniforme e che l’accelerazione ne è un dato accidentale, e compia insomma l’errore che Galileo aveva commesso nel giovanile de motu ma che si era guardato dal ripetere già nelle Mecaniche, nelle quali, stabilendo da un punto di vista rigorosamente statico la inversa proporzionalità tra momenti e linee dei piani, si era astenuto dall’estrapolare alla caduta il legame apparentemente così naturale tra momenti e velocità

        In realtà, l’interesse prevalente del Baliani sembra rivolto qui a stabilire il confronto tra la rapidità con cui avviene il moto di caduta lungo le diverse inclinazioni piuttosto che a dirimere se la velocità varia o meno in uno stesso moto di caduta. In un certo senso, infatti, la proposizione può coesistere sia con il presupposto della costanza delle due velocità, sia con quello del loro simmetrico e proporzionale aumento rispetto agli spazi percorsi sull’inclinata e la perpendicolare. Ma su quest’ultimo punto il Baliani non si esprime, lasciando la questione del tutto impregiudicata. Il lessico stesso, a questo proposito sempre sfuggente e approssimativo, denota la scarsa rilevanza deliberatamente assegnata al concetto di velocità, e la sua relativa ininfluenza nell’uso e nella concatenazione deduttiva. Certo, appare inconcepibile che nel 1638, e nell’opera di uno studioso che conosceva da più di un ventennio l’ambito dei problemi e dei paradigmi galileiani, si pretendesse ancora di affrontare il moto di caduta trascurando ogni definizione e tematizzazione del concetto di velocità. Eppure è proprio quanto fa il Baliani, che vuole disimpegnarsi da ogni asserzione circa la sua crescita. Occorre aspettare la seconda edizione del Libro I per trovare un accenno al suo continuo variare lungo il piano inclinato, e anche qui l’inciso è tanto fugace da suggerire la deliberata intenzione di trascurare il problema. Ora, non c’è dubbio che il Baliani sia giunto a riconoscere 1’esistenza dell’accelerazione ben prima del 1638. Egli si comporta però come se tale fenomeno fossenon definibile, non controllabile, non calcolabile a livello sperimentale, e dunque da espungere anche a livello teorico. Inoltre, come vedremo, riteneva di poterne prescindere, e di conseguenza scelse di non fare alcun cenno al variare della velocità”.

        Sulla questione delle velocità e dei momenti, sulla necessità che su questi argomenti vi fosse un qualche chiarimento, intervenne anche il matematico gesuita milanese Luigi Confalonieri (circa 1600-1653). Costui era persona molto colta particolarmente in matematica e, a suo dire, non altrettanto in filosofia naturale per cui in qualche modo erano complementari con Baliani. Da bravo gesuita era era un esempio di doppiezza dottrinale in quanto da una parte (quella nascosta e privata) si professava antiaristotelico (ed addirittura atomista) ma nella sua pubblica professione di insegnate era un intoccabile ortodosso. Con Confalonieri, Baliani diventò amico ed ebbe con lui una fitta corrispondenza durata vari anni anche proprio sulla questione dei momenti e velocità insieme alle definizioni, petizioni ed alle supposizioni che vi erano dietro (l’insieme degli assiomi che Baliani poneva a premessa del De motu). La discussione che andò avanti non era differente da quanto sollevavano le diverse critiche fatte al De motu dai più vari ambienti scientifici.  Il concetto non era chiaro a Confalonieri e questi gli obiettava e chiedeva più volte ma Baliani o si trincerava dietro i nomi di Stevin e Galileo, che avrebbero dimostrato quanto gli si chiedeva, o tergiversava senza chiarire nulla. Si deve a Costantini uno studio approfondito dei rapporti esistenti tra Confalonieri e Baliani (nell’ambito dell’articolarsi delle discussioni relative al De motu), studio dal quale attingo per completare l’illustrazione dei problemi di Baliani nello studio del moto, particolarmente sulla confusione esistente nei concetti già varie volte ripetuti di velocità e momento.

        Il 3 agosto del 1639 un appassionato di scienze, il genovese Daniele Spinola, scriveva una lettera a Galileo, del quale era seguace ed amico, in cui commentando la lettura dei suoi Discorsi appena arrivati dall’Olanda, parlava di Baliani: Per lo resto, io stimo affatto privo d’intelletto chi sente minor gusto nel leggere il libro di V. S. per la lezione di quello del S.r Gio. Battista Baliani. Non dovrei dirlo, perchè troppo è manifesto; ma già che V. S. s’è compiacciuta di accennarmene alcuna cosa, dico che veramente i supposti del S.r Gio. Battista, appresso di ognuno, han mestieri di gagliarda dimostrazione (come scrissi pure a V. S. nella risposta alla cortesissima sua de’ 12 di Marzo, che dubito ora, con mio disgusto, che non le sia pervenuta); or considerisi qual piacere si può cavare dalle proposizioni fondate sopra di essi, le quali molti stimano che non sian del tutto sue, perchè si vede di dove ponno esser tolte. Ma nel libro di V. S. son congiunte la chiarezza, la facilità, la novità, il diletto, il profitto e la maraviglia in ogni cosa, di modo che non discernendosi qual vi habbia più parte, si conosce camminar tutte all’eccesso con passi eguali. Non debbo però entrar di nuovo a parlare di quello che non so né posso farlo come dovrei. Come si vede il tono di Spinola nei riguardi di Baliani era particolarmente elogiativo. Ma il giudizio iniziava a modificarsi  il 29 ottobre dello stesso anno quando Spinola, in risposta a precedenti giudizi di Galileo (che non possediamo), scriveva queste altre cose ancora a Galileo: Quello che V. S. mi dice del libro sudetto [di Baliani, ndr], è appunto quello che in leggendolo mi diede fastidio. Pensai che nascesse dal mio non intenderlo: e veramente questa è la cagione perchè io non l’ho più veduto; imperocchè, oltre a quegli assunti cotanto oscuri e da non conceder alla prima, parmi che nel progresso del libro l’autore si lasci intendere assai difficilmente. So che mi fa parer questo la mia ignoranza e l’esser avvezzo alla lettura delle maravigliose opere di V. S.; ma né il mio ingegno né le mie occupazioni mi lasciano applicar grandemente a libri sì fatti. Questa accusa di oscurità non era del solo Spinola ma era di molti studiosi tra cui Cavalieri e, appunto, Confalonieri che iniziava a non capire a partire dalla quarta supposizione del De motu, che così recitava:  Il momento di un grave sopra un piano inclinato sta alla sua gravità come la perpendicolare all’inclinata, se la perpendicolare e il piano inclinato vengono descritti a partire dallo stesso punto e fino al medesimo piano orizzontale; perciò in tal caso il rapporto tra gravità e momento è reciproco di quello tra le linee lungo le quali il grave si muove. Questa frase era oscura per molti studiosi, tra cui i citati.Scrive in proposito Costantini:

“La dimostrazione del Galilei chiamata dal Baliani a riprova del suo assunto nella prefazione del De motu gravium incontrava, almeno da parte del Confalonieri, qualche opposizione mentre le esperienze direttamente condotte dal Baliani, cui nello stesso luogo si accennava, non erano nel libro altrimenti illustrate. Ecco come Baliani descriveva tale esperienza al Confalonieri [7 gennaio 1639]: «Rispetto alla 4″ supposizione … io non ne ho fatto pruova esatta, ho però fatto far lo stromento ABC [vedi figura seguente, ndr] in cui AB è una tavola o sia piano declinante, AC è piede mobile snodato in A che dà comodità di poter ridur il piano quanto si vuole più o men declinante con la girella D in cui involta la fune EDF e attaccatavi la palla F di ferro di libbre 34 nella parte E io andava crescendo e sminuendo il peso in modo che con la palla stessero in equilibrio, non esattamente percioché nol permette il contrasto che fa la palla col piano, ma così alla grossa, ove ho osservato che il peso E è minor di quello della palla F quanto è minor la perpendicolare DG del piano declinante AB».

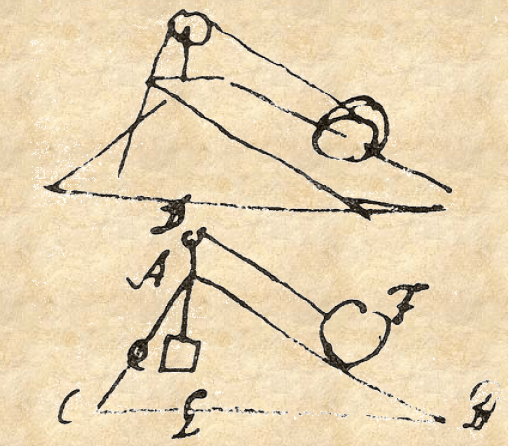
In questi termini l’esperienza non era ignota al Confalonieri, […]. Lo stesso Baliani però doveva insistere sulla sua non conclusività, data l’impossibilità di calcolare gli effetti del «contrasto» del grave sull’inclinata, tanto che di essa, scriveva, «non mi sarei fidato in modo di porre tal propositione per principio che non mi fossi assicurato con esperienze più esatte della verità, se non ne havessi vedute le pruove nello Stevino e Galilei come ho detto nella prefatione». Le difficoltà proposte dal Confalonieri, per altro, riguardavano piuttosto la trattazione geometrica del problema. [Ma Baliani, nella stessa lettera del 7 gennaio, così proseguiva:] «Ove io tratto de pesi considero solo il peso prescindendolo da qualonque figura e se pure volessimo considerarlo con la figura sferica io crederei che sul punto A si havesse a porre il centro di essa sfera o là alcun punto della superficie di essa, il qual centro non stimo che a V. P. debba parer necessario che si muova sopra detto piano, ma che basti che descriva una linea parallela a quella sopra di cui la sfera si sostiene». Chiarendo il proprio obbiettivo Confalonieri doveva riproporre il quesito: «mi scusi – scriveva – se contro l’avviso da lei datomi, considererò il grave sotto qualche figura. Perché trattandosi di isperienza, la quale è pur forza che si faccia con grave figurato, non pare che il mio giuditio si possa ridurre a prendere il grave così in astratto». Prescindendo assolutamente dalla figura del grave, si sarebbe compromessa la possibilità stessa di un approccio geometrico al problema e d’altra parte «non venendo a mio parere variata la verità delle sue propositioni dalla varietà delle figure, potrò meritare qualche scusa se per maggior chiarezza exemplificarò in un grave figurato. Ma cheché sia di ciò – proseguiva mi conceda per grazia licenza che proponga il mio pensiero come l’ho nell’animo, perché io son simile alli preti di villa, che non sanno leggere se non nel suo libro». Certo, la simpatica boutade del Confalonieri era solo in apparenza un’espressione di modestia: la sua insistenza era volta a sollecitare una discussione sul terreno geometrico, ch’egli sentiva non solo come congeniale a sé, ma come decisivo per la nuova fisica.”

        Ma a domande diverse, a sollecitazioni continue, Baliani sfuggiva evitando addirittura di rispondere come se la domanda non fosse mai stata fatta. Al massimo si chiudeva dietro Galileo e Stevin: «io per hora – scriveva il 26 gennaio 1639 – risponderò solo con far riccopiar la propositione del Galilei accennata nella mia prefattione, con che stimo debba rimaner sodisfatta». Con ciò, al contrario, si tornava di nuovo al punto di partenza fino a sfinire completamente Confalonieri che non andava oltre riservandosi solo a dirle un giorno a bocca due mie difficoltà. Abbiamo già visto come operava Baliani con Galileo e non deve stupire questo suo atteggiamento, semmai è straordinario che lo faccia con un suo amico.

        Fin qui ancora sulla quarta supposizione del De motu. Ma vi era altra questione, il secondo postulato del De motu secondo il quale dalla proporzione esistente tra i momenti sarebbe stato possibile dedurre la proporzione tra le velocità. E Baliani diceva a Confalonieri (ancora nella medesima lettera): «Io non credo che sia possibile con esperienze veder con che proportione cresce la velocità nel moto de corpi gravi, solo molto alla grossa, havendo comodità di farla con altezze molto grandi, vedendo il maggior tempo che contenesse da una altezza che dall’altra; non credo però che di tal esperienza si potessi chi che sia totalmente fidare e che solo si possa questo rintracciare con ragioni didotte da altre esperienze più facili a vedere». E Costantini aggiunge:

“Possibile era invece, secondo la quarta supposizione, determinare la proporzione dei momenti e pertanto dedurre da questa quella delle velocità: «se gli antichi e Aristotele et Euclide e tanti altri dopo di loro han preteso di cavar la proportione delle velocità dai pesi, il che io per esperienze esattissime vedo riuscir falso, sia lecito a me cavarla da momenti, non sapendo veder in ciò cosa in contrario».

        Nel rifiuto della tesi aristotelica Confalonieri concorreva prontamente «repugnando troppo apertamente l’isperienza in ciò et altre cose alla dottrina d’Aristotele». Anche la deduzione delle proporzioni delle velocità da quelle dei momenti gli appariva «molto ragionevole»; «non però vedo sia necessaria, – aggiungeva – restando ancora altri capi dalli quali pare che si possan prendere».

        Qui era la nozione stessa di momento, nell’utilizzazione fattane dal Baliani, che il Confalonieri voleva confrontare con quanto in materia era venuto, per proprio conto, elaborando.”

        E Baliani sfuggiva dalle richieste di Confalonieri questa volta dicendo che quanto chiedeva Confalonieri era proprio ciò che diceva lui. Al Confalonieri non sembrava che le argomentazioni di Baliani potessero risolvere davvero l’ambiguità rilevata nella nozione di momento, quale era utilizzata dal Baliani, e insisteva nelle sue obbiezioni portando continue prove ed argomentazioni di differenti autori. Ma con Baliani non si riusciva ad avanzare ed è chiaro che ormai la discussione si alimentava soltanto di un equivoco relativo alla formulazione verbale del concetto di momento che Baliani non è stato mai in grado di precisare. Riuscì solo a riconoscere tempo dopo l’imprecisione della formula adottata nel De motu: «rispetto al momento io dubito di essere stato scarzo nelle parole in dichiararlo, perché ove dico: est excessus virtutis supra motus impedimenta, io dovea per aventura aggionger parole che più chiaramente significassero che l’eccesso s’intende haver tal proportione sopra gli impedimenti, che al’hora i momenti sono uguali quando è la stessa proportione fra l’eccesso del primo sopra i suoi impedimenti che fra l’eccesso del secondo sopra i suoi; e tal commento io vi stimo necessario percioché altrimenti le conseguenze che io ne deduco non sarebbon vere, né sarebbe vera la XI propositione [della quale ho già discusso, ndr] e tutte le seguenti che ne nascono … Da che si vede che io infatti non discordo dal senso di V.S.; ma se ho errato è stato sol in non dichiarar ben il termine momento secondo la mia intentione».

        Su critiche dello stesso tenore e ripetute interveniva ancora Cavalieri. Egli, come accennato, continuò con il suo avversare le supposizioni di Baliani ed il concetto di momento da lui introdotto e dal quale discendevano tutti gli altri ragionamenti. Ancora a Rocca il 2 ottobre 1640 scriveva presentando un argomento estremamente chiaro e dirimente di ogni questione:

Siccome due pesi dell’ istessa materia, ma diseguali, posti in bilancia di braccia eguali non staranno in equilibrio, ma prepondererà il maggiore, che perciò mostrerà essere maggiore il suo momento di quello dell’ altro, e tuttavia gl ‘istessi pesi sciolti, e lasciati cadere liberamente, saranno equi veloci per l’ ossservazione de’moderni, com’ella dice; così dico, che se intenderemo la sfera sostenuta nel detto piano acclive, ed equilibrata da un altro peso [ … ] e se invece di questo contrappeso vi si mettesse una sfera eguale alla data nel piano accliive, il momento di questa saria doppio del momento di quella; ma nondimeno considerati poi sciolti non avriano nelle loro velocità da conservare l’istessa proportione de’loro momenti, come equilibrati; e però parmi, che altro sia il gravitare sopra un piano, altro la velocità con che si muove in quello.

        Insomma: due pesi diversi posti sui due bracci uguali di una bilancia non si fanno equilibrio perché il maggiore che ha momento maggiore farà pendere la bilancia dalla sua parte. Poi però se si considerano i due pesi differenti e si lasciano cadere essi lo faranno con equivelocità. Ciò mostra in toto la fallacia dei ragionamenti di Baliani che associava le cadute dei gravi ai loro momenti. Cavalieri aveva poi da ridire sul momento applicato nel piano inclinato. Non riusciva a convincersi che il tratto che il grave avrebbe dovuto percorrere lungo la linea obliqua si sarebbe potuto sostituire con il dislivello verticale poiché ciò risultava incompatibile con il concetto di velocità del medesimo grave lungo la linea obliqua. E’ un poco l’obiezione analoga a quella che aveva fatto Confalonieri che Cavalieri, ancora nella medesima lettera a Rocca del 2 ottobre 1640, esplicitava nel modo seguente:

«La ragione del Sig. Galileo, e degli altri, che trattano questo teorema, credo sia perché salendo per esempio una sfera sopra un piano acclive colligata con un’altra descendente perpendicolare all’orizzonte, essendo tanta la salita sopra l’acclive, quanta la scesa per la detta perpendicolare, l’altezza della salita all’altezza della scesa è come la perpendicolare all’inclinata: veda ora, se li pare che questi alzamenti e abbassamenti perpendicolari siano sufficienti, o no, a determinare giustamente i loro momenti, il che come appaia evidentissimo nella libra, qua però non mi pare che cammini con pari evidenza»

          Vi sarebbero varie altre cose da dire, cose che sono approfondite dai citati Baroncelli⁽¹⁹⁾ e Costantini. Per quel che mi riguarda ho discusso già troppo di questa vicenda ed ora non mi resta che concluderla con quanto Galileo dettò al suo ultimo allievo, Vincenzo Viviani, a proposito dell’opera di Baliani con il titolo Sopra i principii del Baliani.

«Nel venir poi alla elezione dei principij, sopra i quali deve esser fondata la scienza, prendete come chiara notizia accidenti, i quali niuna connessione hanno con moti fatti sopra linee non rette, non di assegnabile inclinatione, né che in esse le diverse lunghezze operino quello che operano nelle linee rette, ma in tutto e per tutto cose differentissime, lo che mi par grave errore, e tanto maggiore, quanto che e’ se ne tira dietro un altro non minore. Mi dichiaro: voi pigliate come principio noto e indubitato le vibrazioni del medesimo pendolo farsi tutte sotto tempi uguali. siano esse di qualsivoglia grandezza. Item supponete i tempi delle vibrazioni di pendoli diseguali esser tra di loro in suddupla proporzione delle lunghezze dei loro fili, assunto veramente ardito. E da questo che suppponete accadere nei mobili discendenti per circonferenze di cerchi. volete raccorre quello che occorre nei moti retti […]. Che i moti per le parti minime degli archi siano come se fosser fatti per linee rette [è] assunto assai duro, imperocché con gran ragione può il lettore domandare che gli sia assegnata la quantità dell’arco che V.S. chiama minima, sicché, per esempio, ella intenda l’arco esser minimo fino che non giunga alla metà di un grado. […] Ma vegghiamo un’altra disparità massima. Niuno negherà i moti del medesimo mobile, fatti sopra piani di diversa inclinazione, esser tra di loro differenti e che in conseguenza un moto, il quale, cominciato sopra una tale inclinazione debba di parte in parte trapassar sopra altrettante altre diverse inclinazioni, sarà sommamente differente da quello, che sopra una stessa inclinazione deve andarsi continuando. Ora, nella circonferenza del quadrante CB, tante sono le diverse inclinazioni, quante le tangenti, e queste sono quante i punti. cioè infinite, per lo che anca in qual si voglia piccola parte della circonferenza, siccome vi sono infiniti punti, vi sono anche infinite inclinazioni, per la mutazione delle quali non si può dire che il moto per l’arco possa esser simile, non che l’ istesso, che per una medesima inclinazione sola».

        Galileo era durissimo perché oltre all’arditezza delle cose sostenute dal Baliani, vi era un sottile pericolo dietro di esse, pericolo che riguardava la sua persona. Ed il pericolo diventava grande se solo si riflette a quanto già detto alcune pagine più su, e cioè che Baliani si richiamava al giovane Galileo delle Mecaniche e da quelle elaborazioni galileiane ricavava le sue proposizioni. Era quindi vero ciò che sosteneva Baliani, il fatto cioè che le sue conclusioni discendevano da Galileo. Ma quella strada infruttuosa era stata abbandonata da Galileo per intraprenderne un’altra del tutto differente. Inoltre nel De motu spariva l’impostazione archimedea di Galileo per ritornare ad una sorta di sillogismo archimedeo ammantato di parole tratte da un lessico differente. Quel richiamo continuo alla geometria che lo stesso Confalonieri avrebbe preteso da Baliani non c’era più. In cambio ricompariva la classificazione aristotelica nascosta dietro quel continuo richiamo all’esperienza che non si sapeva bene cosa volesse dire se, richiamato da Confalonieri alcune volte rispondeva che tale esperienza non si può fare o, se si faceva, forniva risultati grossolani.

 

IL DE MOTU NATURALI GRAVIUM SOLIDORUM ET LIQUIDORUM (1646). COSA CAMBIAVA

        Le vicende un poco truffaldine che ho raccontato portarono Baliani a modificare il suo lavoro nella seconda edizione, quella del 1646. Venne cambiato l’ordine di alcune proposizioni ed alcune di esse furono modificate. La guida era stata, ma solo fino ad un certo punto, quella di Rocca ed in teoria sarebbe dovuta essere quella di Galileo ma la cosa fu impossibile a Baliani perché se avesse preso tal decisione avrebbe dovuto riscrivere tutto da capo. Dovette quindi accontentarsi di richiamarlo sempre per le sue Mecaniche giovanili anche perché ormai Galileo era morto e non avrebbe più obiettato.

        Ma, contrariamente a quanto la logica potrebbe far prevedere, quella Proposizione XI del Libro I che affermava la proporzionalità inversa tra l’inclinazione del piano e la velocità del grave discendente (Si Duo gravia descendant alterum super linea perpendiculari, alterum vero super inclinata; proportio velocitatum est reciproca proportioni linearum), non fu modificata. Fu invece modificata, perché fosse in accordo con la XI, la dimostrazione della Proposizione XIV (Proposizione che restava invariata). Nel sistemare una connessione logica egli creava però altri problemi come ben ha analizzato la Baroncelli:

Si ricorderà che la proposizione XIV determina lo spazio che, sull’inclinata, il grave percorre a partire dalla quiete nello stesso tempo impiegato a cadere lungo la perpendicolare: vi si dimostra che tale spazio è uguale alla proiezione della perpendicolare sull’inclinata. Il Baliani non rinuncia ad utilizzare la proposizione XI, che cita correttamente, questa volta, per collegare spazi e velocità; in questa citazione, tuttavia, sostituisce in modo arbitrario la velocità lungo l’intera inclinata con quella lungo la proiezione della perpendicolare sull’inclinata, tratto che – si deve dimostrare – è percorso nello stesso tempo della perpendicolare. In sostanza e, ovviamente, senza dichiararlo, egli considera le velocità acquistate dopo tempi uguali lungo la perpendicolare e l’inclinata, e dimostra che esse stanno come gli spazi percorsi. Qui lo scienziato afferma per la prima volta che le velocità lungo le due traiettorie non sono uniformi: ha provato infatti che esse crescono nello stesso rapporto degli spazi […]. Ne conclude – dopo averlo implicitamente supposto – l’uguaglianza dei tempi impiegati […]. Forte di questa conclusione, il Baliani procede nel suo sottile restauro, che gli permette di eliminare le più evidenti incongruenze della precedente versione: la proporzionalità tra inclinate e tempi a pari distanza verticale dalla quiete, dimostrata nella proposizione XXII della prima edizione, diventa qui oggetto della proposizione XV. Così le dimostrazioni successive corrono senza intoppi, fondandosi su quest’ultimo enunciato, equivalente alla proposizione XIV. Lievi aggiustamenti nella numerazione delle proposizioni e nella tecnica dimostrativa, ora più agile, percorrono il libro, lasciandolo tuttavia, quanto al resto, sostanzialmente immutato.
Il Baliani si è finalmente reso conto dell’impossibilità di prescindere dalla variazione della velocità in uno stesso moto di caduta, anche se tale consapevolezza è ben lungi dall’essere formalmente dichiarata o attentamente scandagliata. Al tempo stesso non è disposto a rinunciare al concetto di momento, l’unico che gli permette di spiegare l’indipendenza del moto di caduta dalla massa e che gli garantisce un plausibile legame con le velocità dei gravi lungo diverse inclinazioni. Così ‘momento’, da ora in poi, resterà curiosamente più collegato al ritardo opposto al movimento dalla resistenza e materialità del corpo che alla efficacia della gravità, mentre un nuovo concetto, quello di ‘impetus‘, subentrerà a connotarne la velocità e la propensione al moto.

        Ma anche qui continuò la confusione perché Baliani utilizzò l’impeto come una sorta di strumento in grado di risolvere ogni problema con opportune modifiche qua e là. Lo scopo era quello di differenziarsi da Galileo e certamente Baliani vi riuscì con un lavoro che riscosse l’approvazione degli ambienti conservatori, soprattutto gesuiti che vedevano in lui una personalità da contrapporre a Galileo, e che produsse il suo isolamento dagli scienziati che più si erano mossi sulla strada aperta proprio da Galileo che iniziava a stagliarsi come preciso spartiacque. Occorre però dire che dal 1642 al 1648, dopo la morte di Galileo, soprattutto in Francia sorse un nuovo Affare Galileo. Questa volta lo scandalo era relativo alle leggi galileiane del moto che furono aspramente criticate. All’origine del nuovo affare (1642) vi era la pubblicazione del libro di Gassendi  De motu impresso a motore traslato, libro scritto nel 1640, due anni dopo i Discorsi di Galileo che Gassendi aveva letto con molta attenzione. La data di chiusura dell’affare è invece il 1648, in corrispondenza della morte di Marin Marsenne che, di fatto, era stato l’anima dell’affare. Non seguirò tutta la vicenda, perché ci porterebbe troppo lontano, ma almeno un cenno ad essa occorre farlo (rimandando al lavoro di Galluzzi per una trattazione completa). Fin dal 1633, appena dopo la pubblicazione del Dialogo di Galileo, Mersenne fu profondamente interessato ai lavori dello scienziato pisano ed in particolare a quelli sul moto. Lo stesso Mersenne citerà diffusamente i lavori di Galileo nel suo Harmonie Universelle del 1637. Oltre a ciò occorre tener presente che nel 1634 Mersenne aveva pubblicato alcuni risultati della meccanica di Galileo mentre nel 1638 pubblicò una libera trascrizione di parte dei Discorsi nel suo Le nouvelles pensées de Galilée. Grazie all’intensa attività epistolare, Mersenne coinvolse nell’affare i gesuiti Pierre Le Cazre e Honoré Fabri oltre a Boulliau, Roberval, Le Tenneur e, più marginalmente, Descartes e Pierre Fermat. In Olanda, su impulso ancora di Mersenne, fu interessato Christiaan Huygens, e, più avanti nel tempo, durante un soggiorno in Italia tra la fine del 1644 e l’inizio del 1645, Mersenne coinvolse nella discussione Evangelista Torricelli e Michelangelo Ricci. Tornato in Francia, con altre lettere, coinvolse anche Baliani.

        La chiave della polemica era, come accennato, nel libro di Gassendi  De motu impresso a motore traslato, nel quale l’autore, sincero estimatore di Galileo, faceva emergere con forza l’intrinseca connessone tra il cosmo copernicano, la nuova filosofia e la scienza del moto proposta da Galileo. Le leggi del moto di Galileo erano dunque individuate come sostegno al copernicanesimo e per questo contro di esse partì una campagna di denigrazione orchestrata dai gesuiti, campagna che vide anche Gassendi come bersaglio. I gesuiti lanciarono il loro attacco alle concezioni cosmologiche e filosofiche che discendevano da Galileo ed erano state molto ben riprese da Gassendi, anche profittando del dichiarato atomismo di quest’ultimo. Sostenevano che l’insieme di tali posizioni non potevano essere apprezzate da uomini colti e pii. E poiché nella trattazione del moto di Galileo e Gassendi nelle qualità in considerazione sparivano le forme (restando solo la sostanza), risultava impossibile separare le forme (non esistenti) dalla sostanza. Ciò avrebbe creato un grave problema teologico nel mistero dell’Eucarestia: formae accidentariae nullae sunt, multoque minus inveniri et esse possunt ab omni substantia separatae. Quid sanctioribus igitur nostrae Religionis mysteriis fiet ? Ed ancora una volta si andava ad urtare su questioni di fede che venivano usate come randelli, questa volta per portare l’attacco a Gassendi, visto che Galileo era morto. Per salvare il mistero dell’Eucarestia occorreva allora sbarazzarsi delle leggi del moto di Galileo e quindi di Gassendi. Agli attacchi Gassendi rispondeva sempre in modo puntuale reclamando, tra l’altro, la  libertas philosophandi nelle indagini fisiche aggiungendo che l’atomismo era completamente ammissibile con la fede cristiana e che esso, la fisica e la filosofia di Galileo, costituivano un sistema straordinariamente e sperimentalmente congruente con il mondo copernicano. Negli attacchi a Galileo e Gassendi intervenne anche, a partire dal 1643, il matematico e teologo gesuita francese Honoré Fabri (1607-1688), aiutato dal suo allievo e portavoce Pierre Mousnier, installatosi a Roma dal 1646, che indirizzò sull’argomento una lettera a Gassendi. La lettera partiva gesuiticamente con i migliori propositi: sottomettere i fenomeni naturali a rigorosi trattamenti matematici, rerum physicarum et mathematicarum communio, e prendere le distanze dalla fisica scolastica. Poi passava a descrivere un sistema del mondo di tipo tychonico con leggi del moto confacenti e quindi concludeva con il rifiuto del sistema copernicano che, era sottinteso, doveva prevedere il rifiuto delle leggi del moto che da esso discendevano (quelle di Galileo). Alla fine Fabri informava Gassendi di aver scritto un De motu locali basato su proposizioni rigorosamente geometriche. Questa lettera ebbe un seguito e Fabri divenne un riferimento per altri corrispondenti. In particolare in una successiva lettera a Mersenne sostenne che nel moto naturale, gli spazi percorsi in tempi uguali (partendo dalla quiete) non aumentano come afferma la legge dei numeri dispari di Galileo, ma in accordo con i numeri naturali. Egli avrebbe derivato tale proporzione da un rigoroso studio causale del moto che, per il gesuita era prodotto da impetuosità: gradi di uguale impeto erano acquistati in singoli istanti di tempo e la velocità del moto aumentava a cusa della somma degli impeti. La ragione che indusse Fabri a proporre l’aumento degli spazi percorsi in proporzione alla serie dei numeri naturali era basata sulla sua concezione di istante. Egli considerava il continuo composto di punti o indivisibili. Per Fabri il continuo, una linea ad esempio, non è divisibile nei fatti (attualmente) fino all’infinito ma solo in potenza. Allo stesso modo parlava di atomi di uguale tempo, istanti fisicamente finiti, a ciascuno dei quali corrisponde la produzione di un grado di impeto e, di conseguenza, uno spazio percorso. Nel secondo istante, poiché il primo impeto risultava conservato, i gradi di impeto diventavano due e quindi lo spazio percorso era doppio. E così via. Marsenne obiettò che le cose sembravano dar ragione a Galileo. Fabri rispose affermando che quei risultati erano stati ricavati dal fatto che la comune misura dei tempi che si utilizza per misurare i tempi di caduta e la proporzione degli aumenti di velocità non è mai un istante, ma un’infinità di essi. E  se si riducono le parti dei tempi che si sono considerati come istanti, si troverà che lo spazio percorso risponde all’incirca alle esperienze di Galileo e di V.R. In definitiva Fabri stava costruendo un apparato verbale, una nuova metafisica, con il quale affermava che le leggi galileiana erano in definitiva come quelle sue con una diversa definizione di istante. In realtà le cose erano profondamente differenti perché la sua ipotesi di istante finito ed indivisibile implica che l’accelerazione sia un processo discontinuo, l’integrazione di istantanei e mai crescenti gradi di velocità uniformi. In tal modo un corpo in caduta con partenza dalla quiete non passa attraverso tutti i minori gradi di velocità, come Galileo aveva affermato, ma inizia il moto con un determinato grado di velocità. La proporzionalità dell’aumento degli spazi percorsi in tempi uguali con i numeri naturali era quindi dovuta alla definizione molto stravagante di istante. Mi sono soffermato su Fabri perché avrà un ruolo importante come antagonista di Galileo, risultando personaggio che trovava leggi analoghe (solo apparentemente) a quelle di Galileo a partire da postulati differenti.

        Naturalmente le cose non finirono qui perché pian piano nuovi interlocutori si inserivano e Mersenne tentò di convincere anche i diretti discepoli di Galileo, Torricelli e Ricci, degli errori insiti nelle leggi del moto di Galileo. Per costoro era però una riedizione (o un’appendice) degli indegni e criminali attacchi al maestro del 1633. Si rifiutarono di partecipare a quelle discussioni fomentate da quel frate dei Minimi, Mersenne, che era stato un assiduo depredatore delle migliori cose fatte dagli scienziati italiani e che ora diventava il denigratore del maestro di tutti. Non così reagì Baliani che, come abbiamo visto, aveva stretti rapporti con i gesuiti e che, non a caso, modificò il suo De motu proprio in quegli anni. Mentre la prima edizione, seppur in modo confuso come abbiamo visto, prendeva le mosse da Galileo, questa seconda era incentrata sulle teorie fisiche di Fabri. Le pressioni dei gesuiti non erano riuscite a convincerlo sulla negazione del vuoto ma a smuoverlo sulla strada della messa in discussione delle leggi galileiane del moto si. Baliani sostenne infatti che nella caduta libera l’aumento degli spazi percorsi in tempi uguali va come la serie dei numeri naturali a partire dall’unità. E Baliani giustificò questo sorprendente risultato, che significava un grossolano errore in uno dei punti chiave del De motu, affermando il suo accordo con la teoria di Fabri degli istanti indivisibili o atomi di tempo; egli sostenne che dal punto di vista dell’esperienza vi era perfetta equivalenza fra la sua ipotesi e quella di Galileo, utilizzando le stesse argomentazioni di Fabri. Ed aggiunse, in accordo in ciò con i pensieri di Mersenne degli ultimi anni sul problema del moto ed in completa opposizione a Galileo, la necessità di una spiegazione causale del moto come conseguenza dell’irrealizzabilità di verifiche sperimentali. Quanto dico lo si ritrova nella parte finale dell’Introduzione al Libro Quarto del De motu, Sul moto dei gravi e libro primo dei liquidi, dove si legge:

Se non erro, dunque, il moto si incrementa secondo la progressione aritmetica naturale, e non secondo quella, fin qui accreditata, dei numeri dispari a cominciare dall’unità; nondimeno, derivando da entrambe le leggi effetti impercettibilmente discrepanti, e dunque quasi identici, non c’è da meravigliarsi che si sia creduto che gli spazi stessero tra loro come i quadrati dei tempi; pur non essendo del tutto esatta, infatti, tale legge è tanto vicina a quella vera da risultare indistinguibile da essa al giudizio dei sensi e al vaglio di osservazioni sperimentali mirate ed appropriate, e pertanto occorre giustificare chiunque l’abbia ritenuta valida.
La sola cosa a cui tendevo era la scoperta di una verità finora ignota: chiarire la causa di quella proporzione e, insieme, la natura degli errori presenti nelle supposizioni e negli esperimenti fin qui impiegati; altri giudicherà se abbia davvero raggiunto lo scopo.⁽²⁰⁾

        Non si tratta di plagio, come osserva Galluzzi, ma dell’accettazione di un clima, della pressante e continua suggestione ricevuta dai gesuiti con cui era in contatto. Ed infatti nessuno accusò Baliani di aver ripreso per intero la teoria di Fabri e di averla presentata come farina del suo sacco. Ed in una lettera di Baliani a Mersenne del 13 marzo 1647 troviamo la prova dell’influenza diretta di Fabri su Baliani. Baliani infatti confessava che in un recente passato era andato a trovarlo Fabri e con lui avevano discusso a lungo sul problema del moto trovando pieno accordo (E’stato qui il P. Onorato Fabri con cui ho trattato con molto gusto e mi pare un uomo molto dotto e vedo che in molte cose habbiamo dato nell’istessi pensieri). E Fabri, da parte sua, dichiarò trionfalmente che le sue idee erano state recepite in pieno da Baliani. Ed anche Mersenne, nel 1645, era andato a Genova ed era restato in città per diverso tempo, al fine proprio di conversare con Baliani.  I gesuiti, con l’aiuto di un Minimo come Mersenne, ormai potevano fare ciò che meglio credevano all’ombra dell’Inquisizione che terrorizzava. L’altro gesuita, il Cabeo genovese, ebbe ad insistere molto sul fatto che Galileo si era ispirato a Baliani, che lo aveva preceduto, per ricavare le sue presunte scoperte. Nel dire tali sciocchezze esaltava Baliani per la sua modestia che lo aveva indotto a non seguire Galileo nella pretesa di considerare come scienza una serie di proposizioni dipendenti da principi chiaramente falsi. E Baliani arrivò addirittura a protestare con Mersenne perché nel Tomo III delle sue Novarum observationum del 1647 lo aveva presentato come discepolo di Galileo. E per testimoniare che non era vero invocava, come no!, l’altro gesuita, il Cabeo. Aggiungendo che egli non era debitore in nulla verso Galileo nei riguardi del quale reclamava sue priorità in completa assonanza con le sciocchezze già in precedenza sostenute dal medesimo testimone Cabeo. Mersenne promise di dar conto di quanto Baliani gli aveva detto e la promessa venne mantenuta con uno scritto che fu inserito nell’edizione italiana delle Opere diverse di Baliani del 1666:

Ho gran gusto che V.S. mi habbia imparata per l’ultima sua che Galileo non sia il primo che ha osservato la proportione del moto de i corpi gravi che cascano giù, perché io pubblicherò a tutti quanti che in ciò siete stato il primo Osservatore, come l’ha confermato il P. Cabeo nel luogo citato da voi nelle sue Meteore.

        Così Baliani, adulato da amicizie interessate e stimolato da un forte senso di emulazione verso Galileo, fece un gravissimo errore che compromise seriamente la sua reputazione così come tutti gli storici ammettono. Baliani risultava la vittima involontaria, o il suicida intellettuale, dell’affare Galileo sulle leggi del moto.

IL SEGUITO DEL DE MOTU ED ALTRI LAVORI

        Il De motu proseguiva con lo studio della percossa nel quale veniva introdotto un concetto, analogo alla quantità di moto di Descartes, proporzionale al prodotto di gravità ed impeto. Oltre a ciò vi è da sottolineare la riuscita di Baliani  a trattare la percossa e a trovare risposte con considerazioni di tipo dinamico, settore nel quale Galileo non era riuscito ad entrare pur essendosi cimentato con esso più volte. Qui la trattazione di Baliani è originale e non ha continui possibili richiami a Galileo e qui il suo aiuto al secondo affare Galileo riuscì a farsi sentire. Inserirsi in questioni nelle quali Galileo non era stato in grado di trovare soluzioni era gratificante per un Mersenne che era entrato in pieno nel mondo della metafisica del suo protetto Descartes e cercava in ogni modo di esorcizzare l’unico grande avversario.

        Altri argomenti trattati, come il moto dei liquidi, non meritano attenzione perché sono riscritture di argomenti ben noti ad ogni studioso del tempo. Semmai è utile fare un’osservazione a margine. Qui Baliani, se avesse avuto più coraggio ed indipendenza di giudizio, avrebbe potuto elaborare quanto trovato nel suo lavoro con il sifone del 1630. La scoperta della pressione dell’aria avrebbe integrato e reso molto importante lo studio che egli fece negli ultimi tre libri del De motu, libri che ripetono invece per i liquidi quanto detto per i solidi. Non si hanno inoltre prove di un contatto con Torricelli a proposito dei suoi lavori sul vuoto e sul barometro del 1644. Sembra sia stato Mersenne ad informare Baliani solo nel 1647 forse per sua fortuna altrimenti si sarebbe dovuto schierare a sostegno del vuoto contro i suoi cari gesuiti. Un indiretto contatto però vi fu ed era indiretto perché gli allievi di Galileo furono isolati dalla politica orchestrata dai gesuiti e con loro si parlava con intermediari. Torricelli era un sostenitore del moto parabolico dei proiettili in perfetta sintonia con Galileo ed in completo disaccordo con Baliani e ne aveva trattato nel suo De motu del 1644 che conteneva due capitoli, uno dedicato ai proiettili (De motu proiectorum) ed uno alle acque (De motu aquarum), lavoro che doveva essere ben conosciuto da Baliani. Fu l’astronomo Renieri, corrispondente anche di Galileo, oltreché di Baliani, a chidergli spiegazioni su quel moto. Torricelli rispose con grande disponibilità anche se le domande si facevano insistenti al modo che abbiamo visto utilizzato da Baliani con Galileo. Torricelli ad un certo punto comprese che quelle domande provenivano da uno che denigrava Galileo sul moto di caduta dei gravi e rispose piuttosto seccato a Renieri che credeva di aver scritto piuttosto ai filosofi che ai bombardieri. Fu proprio Torricelli che intervenne sulle posizioni di Baliani relative al moto di caduta che sarebbe dovuto andare secondo la serie dei numeri naturali. Egli semplicemente osservò che per demolire quella sciocchezza bastava una sola considerazione: se la serie degli spazi successivi percorsi in tempi uguali andasse come la serie dei numeri naturali, dovrebbe farlo anche a tempi raddoppiati, ciò che non avviene perché la natura non fa questi spropositi.

        Baliani fu conosciuto soprattutto per il De motu ma scrisse anche altro. Nel 1647 pubblicò un lavoro sulla peste, il Trattato della pestilenza, nel quale propose una spiegazione chimica per i sintomi di quella micidiale malattia e sulla facilità di contagio. Egli prendeva in esame il corpo umano e il suo funzionamento, la costituzione dei corpi naturali, ma soprattutto sviluppava la sua visione complessiva del mondo fisico, incentrata sulla teoria del lume (della quale aveva in precedenza discusso nella corrispondenza con Confalonieri) o del calore necessario per la sopravvivenza del mondo, mettendo in relazione la crescita della popolazione con la disponibilità di cibo. La teoria che vedeva la luce nel libro sulla peste, era così riassunta dallo stesso Baliani in una lettera dell’agosto 1653 al gesuita Grassi (quello della polemica con Galileo):

«Io stimo che la natura habbia produtto per la struttura del mondo due sustanze, una materiale, l’altra immateriale; che la prima sia divisa in terra, acqua, sale et olio, che sono quelle sostanze che i chimici domandano sal, solfo, mercurio e caput mortuum; che la seconda sia il lume, la quale risieda principalmente nel Sole … et indi si sparga per l’universo».

        Un’ultima questione che merita una qualche attenzione è quella relativa alle maree, legata a fondamentali questioni cosmologiche, che, come si sa, fu uno dei punti di grave difficoltà per Galileo che si basava sull’ipotesi errata che la Luna non esercitasse alcun influsso sulle maree. Il problema si pose nella vecchia corrispondenza di Baliani con Galileo, in una lettera che Baliani scrisse a Galileo il 23 aprile 1632. In riferimento ad un passo del Dialogo di Galileo, Baliani scriveva:

Tutto questo quarto dialogo, ove si tratta del flusso del mare, è per mio avviso meraviglioso, onde tanto più mi do meraviglia, che dove V. S. nelle altre cose leva tutti i dubbi, in questo ne lascia uno di non poco momento senza rispondervi: et è che il flusso dovrebbe esser ogni dì alla stessa hora, e pur l’ oppinione comune è contraria, cioè che si anticipi ogni giorno circa quattro quinti d’hora, per andar esso seguendo il moto della luna.

        Era il primo cenno di cui abbiamo costanza di un Baliani che si occupava delle maree coinvolgendo quindi questioni attinenti al sistema astronomico e quindi ai moti relativi di Terra e Luna. Scrive a proposito Lucio Russo:

Poiché le maree dipendono manifestamente dalle fasi della Luna, Baliani pensò che se si accetta l’ipotesi cinetica galileiana, occorre supporre che la Terra, oltre ai moti di rotazione e rivoluzione, abbia anche un moto di periodo mensile. Mentre questa conclusione era ineccepibile, !’identificazione del terzo moto fu meno felice. A Baliani sembrò che l’unica possibilità di far muovere la Terra con un periodo eguale a quello della rotazione apparente della Luna consistesse nel compiere un ulteriore passo nella direzione di Copernico, declassando il nostro pianeta e facendone un satellite della Luna. Egli suppose cioè che fosse la Terra a ruotare intorno alla Luna, che a sua volta girava intorno al Sole.
Si sbaglierebbe immaginando che la strana teoria, che possiamo chiamare “ultracopernicana”, di Baliani sia stata una bizzarria priva d’importanza per la storia della scienza. In realtà essa, traendo una prima conseguenza necessaria e importante dal confronto tra !’ipotesi cinetica e i dati osservativi, svolse un ruolo significativo, pur se poco riconosciuto, come uno degli anelli di congiunzione tra la teoria di Galileo e quella di Newton. Gli scritti di Baliani sulle maree non furono pubblicati dal loro autore, ma nel 1651 una sintesi delle sue idee fu inclusa da Giovanni Battista Riccioli (1598-1671) nel suo Almagestum novum, dove attirò l’attenzione di uno dei massimi scienziati dell’epoca.

         Baliani quindi tentava una conciliazione di Copernico con Tolomeo introducendo un’ipotesi che prevedeva una Terra in moto intorno alla Luna di modo che quest’ultima potesse esercitare un’influenza meccanica sulle maree (teoria selenocentrica). Era una sorta di sistema tychonico in cui il ruolo di qualche astro veniva scambiato creando una mescolanza tra sistemi astronomici. La storia di questa idea, per chi volesse approfondirla, è raccontata da Serge Moscovici qui mi limito ad un breve cenno.

        Le osservazioni di Baliani a Galileo erano corrette. Nel lavoro dello scienziato pisano non si teneva conto delle osservazioni sperimentali e la Luna non era tenuta in alcuna considerazione. Galileo non rispose a queste obiezioni e il problema posto restò lì fino a quando, come accennato da Russo, Riccioli non pubblicò, nel suo Almagestum novum del 1651, due lettere di Baliani nelle quali la teoria selenocentrica veniva discussa in modo più ampio, anche se come la solito oscuro, per la spiegazione del flusso e riflusso del mare. Prima di queste lettere a Riccioli che erano divenute pubbliche vi era stata una illustrazione della sua teoria in uno scambio epistolare, a partire dal 20 dicembre del 1641, con Confalonieri. Baliani iniziava con l’affermare che il sistema cosmologico di base era quello tychonico solo con questa differenza che la Terra si giri in se stessa e intorno alla Luna immobile rispetto al tutto, ma che girandosi intorno al proprio centro in un mese lunare volti sempre la faccia alla Terra, con che per aventura con qualche analogia a me incognita si rapisca la Terra intorno a sé; che il Sole abbia il moto annuo solamente e gli altri pianeti intorno al Sole. E questa era una prima versione del sistema selenocentrico di Baliani. Ma in epoca più avanzata ne fece una seconda che più semplicemente prevedeva l’inversione delle posizioni di Terra e Luna nell’ambito di un sistema copernicano. La lettera a Confalonieri continuava ampliando il discorso: Quel che ho da proporre è che se il Copernico havesse posto la Luna per centro dell’Universo in vece del Sole, la sua opinione haverebbe avuto per ventura manco dell’impossibile. La cosa, secondo Baliani, sarebbe stata più plausibile con il medesimo argomento introdotto da Tycho per giustificare il suo sistema. Perché, in tal modo, si riduceva la dimensione dell’Universo che con il Sole al centro diventava troppo grande. Diceva Baliani a sostegno di tale tesi che la distanza delle stelle da noi sarebbe tanto minore di quella che è secondo il Copernico, quando è minore il diametro dell’orbe lunare di quello dell’orbe magno e perciò minore stravaganza sarebbe la tanta distanza delle stelle che venisse a risultare dal moto della Terra.

        In una lettera successiva a Confalonieri del 20 dicembre 1641 Baliani comunicava all’amico le obiezioni che aveva già fatto a Galileo:

«Il Gallileo tentò di aquistar per tal opinione [ossia per il sistema copernicano] una gran probabilità dal flusso del mare; tengo però per verissimo, come io ne scrissi subito a lui, che anzi il flusso derroghi a tal moto, atteso che se ìl flusso dipende dal girar della Terra intorno al Sole non può seguire nel modo che segue, perciò che anzi converrebbe che il flusso cominciasse ogni giorno nell’istesso luogo all’istessa hora, il che parlando con persona di tanto intendimento non starò a dichiarare, ma in fatti è vero che ogni giorno si anticipa il flusso di circa quattro quinti d’hora e per conseguenza che seguita il moto della Luna, onde ne nasce che se la Luna fosse il centro dell’Universo e che la Terra vi girasse intorno et havesse anco il moto diurno, par molto probabile che il flusso dovesse succedere a punto nel modo che lo vediamo».

Confalonieri rispondeva il 29 dicembre avanzando anch’egli problemi rispetto alla teoria di Galileo e dicendo a Baliani che sarebbe stato molto utile per la discussione del problema delle maree la soluzione di quello della cicloide:

«V. S. haverà facilmente veduto alcuni problemi mandati da Francia, uno de quali era: “Data una linea retta sopra di cui si mova il centro d’un circolo, il quale si gira in se stesso, assegnare la quantità della cycloide che vien descritta da un punto della circumferentia di detto circolo”. Questo problema ha bisogno di determinatione essendo necessario saper prima che proportione habbi il moto del centro al moto della circonferenza. Ma anco assegnata tal proportione stimo difficilissimo determinare la quantità della cycloide, onde ne pur mi son posto a tentare tal impresa. Ma se alcuno sciogliesse questo problema, haveressimo note le diverse velocità d’un punto della Terra caggionate dalla combinatione del moto annuo e diurno, o, com’Ella propone, menstruo e diurno; dal che potressimo forse cavare qualche maggior probabilità per attribuir il flusso del mare alla diversa velocità del vaso [delle diverse parti della Terra, ndr]».

        Il 15 marzo 1642 Baliani rispondeva mostrando di aver ben capito il senso dello studio della cicloide per la comprensione del fenomeno delle maree e ribadendo il suo restare d’accordo con i presupposti della teoria galileiana. Ed il 14 maggio 1642, in una ulteriore lettera, presentava la sua teoria relativa alla periodicità delle maree basata sulla teoria selenocentrica e proprio su un parziale sviluppo della teoria della cicloide (si veda Costantini, pagg. 48-51). Confalonieri rispondeva il 21 giugno affermando che, a questo punto, non restava che aggiustar la grandezza e moto degli altri cieli e pianeti, per salvare tutte l’apparenze e particolarmente le stationi, retrogradazioni etc., il che però non è molto difficile (sic!).

        Scrive in proposito Costantini:

In realtà sembra che proprio questo problema abbia presentato al Baliani i maggiori ostacoli e con ogni verosimiglianza fu la sua mancata soluzione (non, come pretendeva il Riccioli, lo scrupolo di ripresentare, sia pure in forma ipotetica, la tesi condannata della mobilità della Terra) che costrinse il Baliani a rinunciare alla pubblicazione della sua teoria. Quando l’aveva presentata al Confalonieri, il Baliani non aveva mancato di far precedere l’enunciazione dell’ipotesi da una recisa dichiarazione di fede anticopernicana e di obbedienza alla Chiesa: «io tengo per vero – aveva scritto – solo quelle cose che non ripugnano punto a tutto ciò che tiene la S.ta Chiesa e … perciò stimo falsa l’opinione di Copernico de li moti della Terra, anzi tengo che sia stabile e centro dell’Universo». Nella chiusa della stessa lettera aveva invitato ancora il Confalonieri a considerare la teoria che gli era venuto esponendo «un puro paradosso» e lo aveva pregato di «non partecipare queste stravaganze con chi si sia». Si trattava di cautele indispensabili in uno scritto, sebbene diretto a persona di opinioni spregiudicatamente innovatrici. Ma nella resistenza alle sollecitazioni che il Confalonieri prima, lo stesso Riccioli poi dovevano fargli perché rendesse finalmente pubblica la sua teoria, così come nell’insistenza posta nel presentarla come mera ipotesi, non tutto deve attribuirsi a semplice calcolo prudenziale o a zelo cattolico. Nei confronti del copernicanesimo i dubbi del Baliani avevano preceduto la condanna da parte della Chiesa (persino le scoperte galileiane relative ai pianeti medicei, alle fasi di Venere ed alle macchie solari gli eran parse confermare più il sistema ticonico che quello copernicano) e, soprattutto, in più di un’occasione lo scienziato genovese aveva manifestato la propria convinzione che la molteplicità delle ipotesi cosmologiche fosse irriducibile: solo l’esperienza avrebbe potuto decidere a favore dell’una o dell’altra, ma, appunto, il Baliani mostrava di non credere nella possibilità in questo campo di un’esperienza decisiva. La teoria galileiana delle maree, opportunamente corretta, sembrava militare a favore della tesi di un moto di rivoluzione della Terra intorno alla Luna, ma certo non era senza significato per il Baliani il fatto che anche questa tesi potesse innestarsi in schemi cosmologici diversi. Del resto, nel 1650 dichiarava al Riccioli di non poter dimostrare [come la Luna stia ferma al centro dell’Universo]. La sua restava certamente un’ipotesi possibile ma, come pare, Baliani non credeva più ad una sua maggiore probabilità.
Ponendo la Luna in luogo del Sole al centro dell’Universo si sarebbe ottenuta una maggiore credibilità rispetto alla teoria copernicana in relazione alle dimensioni del Cosmo, ma si sarebbe compromesso uno degli assunti fondamentali della teoria stessa: «per salvare in questa hypotesi l’eccentricità de pianeti colle loro retrogradationi etc, – aveva notato in proposito il Confalonieri – sarebbe necessario per mio credere toglier alli stessi pianeti quell’uniformità di moti di cui tanto si preggiano i copernicani, non bastando la grandezza dell’orbe lunare per simili fenomeni, come forse basta quella dell’orbe magno». Viceversa, lasciando il Sole al centro del sistema e ponendo la Luna al centro dell’epiciclo terrestre, si sarebbe dovuta ammettere, rispetto alla stessa ipotesi copernicana, un’ulteriore, enorme espansione dell’Universo «quod non dubito – dichiarava al Riccioli – quin esset magnum paradoxum».

    Torniamo ora alle lettere di Baliani a Riccioli pubblicate nel 1651⁽²¹⁾ leggendone qualche brano.

Ho considerato ciò che mi avete scritto a proposito del mio sistema e quantunque io persista nel credere che la Terra sia, evidentemente, al centro dell’Universo, non riesco a persuadermi che se il Sole è situato là e la Terra ruoti intorno alla Luna, sia necessario attribuire alla Luna altri moti oltre quelli immaginati da Copernico e quelli che io stesso ho ricercato.

La frase è oscura. Se infatti è il Sole al centro dell’Universo, nessuno vieta di assegnare alla Luna i moti che ha descritto Copernico. Se è invece la Terra al centro la Luna si dovrà per forza muovere intorno alla Terra. Ma Baliani proseguiva:

In effetti m’è sembrato a prima vista che si possono salvare le apparenze e che, a causa dei nuovi movimenti della Luna intorno alla Terra, degni di considerazione, è necessario immaginare una grande sfera molto più vasta di quanto non l’abbia stimata lo stesso Copernico.

Anche con Riccioli sorgeva quindi il problema delle dimensioni dell’Universo affrontato con Confalonieri. E’ invece una novità il passaggio al secondo sistema selenocentrico, infatti non si parla più di moto della Terra intorno alla Luna ma sembra sia accettato il sistema copernicano nel quale Baliani andava a vedere come funzionava il sistema a due corpi Terra-Luna. Baliani affermava di avere scartato il moto della Terra intorno alla Luna per non essere stato in grado di trovare prove in sostegno della sua precedente ipotesi. I nuovi movimenti della Luna, nel sistema di Copernico, dovevano risultare ora dalla composizione del moto della Luna intorno alla Terra mentre questa si sposta intorno al Sole, una sorta di moto epicicloidale. Ma, data questa nuova visione del sistema astronomico per rendere conto delle maree, è possibile credere ad una conversione di Baliani al copernicanesimo, in precedenza chiaramente rifiutato ? Con il senatore genovese non è possibile prendere nulla per definitivo e quindi lasciamo in sospeso la risposta.

NOTE

(1) Scrive Lavaggi:

Nella seconda metà del ‘500 l’ambiente più strettamente scientifico [nella Repubblica di Genova] viveva più che altro di presenze e iniziative individuali, un quadro questo destinato in fondo a non mutare più di tanto con l’arrivo del Seicento. In una lettera spedita intorno al 1590 a Stefano Di Negro dall’illustre letterato genovese Ansaldo Cebà quest’ultimo – che scriveva da Padova – si lamenta del divario esistente fra la cultura genovese di fine Cinquecento e quella della prestigiosa sede universitaria veneta, dove si era recato ad approfondire i suoi studi.
Dalla privilegiata Università padovana, Cebà giudica l’ambiente della sua città provinciale ed arretrato, e a ragione, se consideriamo che mentre in riviera l’aristotelismo era ancora dominante (e lo sarà ancora a lungo, basti considerare una figura peraltro di spicco come Fortunio Liceti), nella città del nord egli aveva la possibilità di entrare in contatto, oltre che con un diffuso ed aggiornato dibattito letterario, anche con personaggi quali Gian Vincenzo Pinelli – possessore di una grandissima biblioteca e in contatto con Galileo – e Paolo Pozzobonello, corrispondente e amico dello stesso Galileo.
L’aggiornamento culturale in un importante centro italiano era d’altra parte fondamentale per la formazione degli uomini di scienza genovesi vissuti tra il XVI ed il XVII secolo, come si può notare facilmente dalle loro biografie: viaggio di formazione immancabile e necessario, che in diversi casi si trasformava addirittura in un definitivo distacco. L’astronomo e matematico Giovan Domenico Cassini, dopo aver frequentato a Genova il Collegio gesuitico, si trasferì presso l’osservatorio di Panzano, vicino a Bologna, e poi a Parigi – chiamato da Colbert per volere dello stesso Luigi XIV- per rimanere al passo con i progressi scientifici galileiani. Non diversamente avvenne in ambito medico, dove Demetrio Canevari si trasferì definitivamente a Roma nel 1584 per esercitare la sua professione, accumulando nel corso della sua vita una vastissima biblioteca, che per suo volere tornò a Genova alla sua morte.
Anche Fortunio Liceti – per citare le personalità più significative – si allontanò da Genova per studiare medicina, e ben presto si trasferì a Bologna e poi a Padova dove ebbe l’opportunità di insegnare in prestigiose Università.

(2) Filippo Salviati (1582-1614) giovane amico ed estimatore di Galileo, fu accademico della Crusca e dei Lincei. A lui Galileo dedicò la sua Istoria e dimostrazioni intorno alle macchie solari che fu scritta nella villa del Salviati a Signa e pubblicata dall’Accademia dei Lincei nel 1613. Morì giovane a Barcellona (Spagna) probabilmente in un qualche duello. Galileo gli era tanto affezionato e tanto lo stimava da assegnargli il posto di uno dei suoi personaggi nel Dialogo sopra i due massimi sistemi del mondo (1632).

(3) Il finto Apelle era il gesuita Christoph Scheiner (1573-1650) con il quale vi era stata una dura polemica con Galileo sulla priorità della scoperta delle macchie solari. Quando Galileo si recò a Roma nel 1611 per far vedere direttamente a molte persone interessate le scoperte astronomiche annunciate nel Nuncius Sidereus (1610), parlò a molti testimoni, tutti concordanti nell’aver sentito Galileo in proposito, delle macchie che aveva osservato sul Sole (l’anno precedente ne aveva già parlato ad altri a Padova e Venezia). Tra questi vi era il matematico ed astronomo svizzero nonché gesuita Habakkuk Guldin, noto con il nome di Paolo Guldino o (1577-1643) che riferì del fenomeno all’altro gesuita, matematico tedesco, Christoph Scheiner. Indipendentemente dalla priorità di una scoperta che spesso è simultanea, la cosa importante è la spiegazione del fenomeno. La dinamica dei fatti ridotta ai minimi termini è che Galileo pubblicò, nel 1612, il Discorso intorno alle cose che stanno in su l’acqua, o che in quella si muovono. In questo lavoro parlò per la prima volta ufficialmente di macchie solari raccontando di averle osservate a Padova nel 1610. Nel 1613 Galileo pubblicò un nuovo lavoro, la Istoria e dimostrazioni intorno alle macchie solari e loro accidenti come risposta ad un lavoro di Scheiner, Tres epistolae de maculis solaribus (1612), che raccoglieva tre lettere inviate a Mark Welser, un politico di Augusta che aveva studiato in Italia, scritte tra il novembre ed il dicembre 1611 e nelle quali Scheiner lo informava di avere scoperto le macchie solari (in realtà fu Welser che raccolse le tre lettere ricevute e, dopo averle pubblicate con il permesso di Scheiner, le inviò a vari studiosi). Poiché i superiori gesuiti ebbero paura di dare il permesso alla pubblicazione di un qualcosa che avrebbe potuto screditarli, Scheiner dovette far firmare le lettere con uno pseudonimo, Apellis latentis post tabulam (Apelle nascosto dietro la tela, con riferimento al pittore dell’antichità che si nascondava dietro la tela per ascoltare non visto i giudizi sul suo lavoro). Galileo capì che si trattava di Scheiner e da allora lo chiamò il finto Apelle. Scrisse due lettere a Welser sulla questione per dare le sue ragioni e per rivendicare di essere stato il primo. Scheiner fu informato di ciò e scrisse un nuovo lavoro sotto forma di tre nuove lettere a Welser, De maculis solaribus et stellis circa Jovem errantibus accuratior disquisitio, lavoro nel quale dava maggiori dettagli sulla sua teoria delle macchie contrastando quella di Galileo data nella seconda lettera a Welser. A questo punto Galileo inviò un’altra lettera a Welser, la terza, nella quale contestava punto per punto la Accuratior disquisitio. Riguardo alla spiegazione delle macchie, mentre Scheiner parlava di piccoli pianeti che eclissavano il Sole, stelle minutissime che congionte in folta schiera si veggano, (anche perché il Sole aveva caratteristiche particolari nella fisica di Aristotele essendo fuoco, il più puro dei quattro elementi che non poteva essere corrotto con delle macchie), Galileo sosteneva che le macchie erano un fenomeno reale (non provocato dal telescopio) che aveva luogo sul Sole, erano qualcosa del tipo nubi che seguiva la rotazione del Sole medesimo (sono contigue alla superficie del corpo solare, dove esse si generano e si dissolvono continuamente, nella guisa appunto delle nugole intorno alla terra e dal medesimo sole vengono portate in giro). Non potevano essere pianetini o stelle perché variavano continuamente dimensioni e conformazione. Infine le macchie partecipavano al moto di rotazione del Sole su se stesso risultando quindi portate in giro dal Sole medesimo. E’ interessante osservare che Galileo parla esplicitamente di rotazione del Sole intorno al proprio asse e la cosa era di per sé pericolosa perché era stata sostenuta apertamente da Giordano Bruno ed anche da Kepler (Astronomia Nova, 1609). Da notare che Galileo parlava anche del fatto che le macchie provavano la corruttibilità dei corpi celesti. Per una ricostruzione dettagliata della questione si può vedere  Camerota da pag. 238 a pag. 259.

(4) Nell’Istoria e dimostrazioni intorno alle macchie solari e loro accidenti Galileo aveva scritto, a proposito del moto del Sole, un paio di pagine (E.N., Vol. V, pagg. 134-135) che prendevano le mosse da una formulazione ancora non definitiva del principio d’inerzia:

Imperò che mi par di osservare che i corpi naturali abbino naturale inclinazione a qualche moto, come i gravi al basso, il qual movimento vien da loro, per intrinseco principio e senza bisogno di particolar motore esterno, esercitato, qual volta non restino da qualche ostacolo impediti; a qualche altro movimento hanno repugnanza, come i medesimi gravi al moto in su, e però già mai non si moveranno in cotal guisa, se non cacciati violentemente da motore esterno; finalmente, ad alcuni movimenti si trovano indifferenti, come pur gl’ istessi gravi al movimento orizontale, al quale non hanno inclinazione, poi che ei non è verso il centro della Terra, né repugnanza, non si allontanando dal medesimo centro: e però, rimossi tutti gl’ impedimenti esterni, un grave nella superficie sferica e concentrica alla Terra sarà indìfferente alla quiete ed a i movimenti verso qualunque parte dell’ orizonte, ed in quello stato si conserverà nel qual una volta sarà stato posto; cioè se sarà messo in stato di quiete, quello conserverà, e se sarà posto in movimento, v. g. verso occidente, nell’istesso si manterrà: e così una nave, per esempio, avendo una sol volta ricevuto qualche impeto per il mar tranquillo, si moverebbe continuamente intorno al nostro globo senza cessar mai, e postavi con quiete, perpetuamente quieterebbe, se nel primo caso si potessero rimuovere tutti gl’impedimenti estrinseci, e nel secondo qualche causa motrice esterna non gli sopraggiugnesse. E se questo è vero, sì come è verissimo, che farebbe un tal mobile di natura ambigua, quando si trovasse continuamente circondato da un ambiente mobile d’un moto al quale esso mobile naturale fosse per natura indifferente? lo non credo che dubitar si possa, ch’ egli al movimento dell’ ambiente si movesse. Ora il Sole, corpo di figura sferica, sospeso e librato circa il proprio centro, non può non secondare il moto del suo ambiente, non avendo egli, a tal conversione, intrinseca repugnanza né impedimento esteriore. Interna repugnanza aver non può, atteso che per simil conversione né il tutto si rimuove dal luogo suo, né le parti si permutarro tra di loro o in modo alcuno cangiano la lor naturale costituzione, tal che, per quanto appartiene alla costituzione del tutto con le sue parti, tal movimento è come se non fosse. Quanto a gl’impedimenti esterni, non par che ostacolo alcuno possa senza contatto impedire (se non forse la virtù della calamita): ma nel nostro caso tutto quel che tocca il Sole, che è il suo ambiente, non solo non impedisce il movimento che noi cerchiamo di attribuirgli, ma egli stesso se ne muove, e movendosi lo comunica ove egli non trovi resistenza, la qual esser non può nel Sole: adunque qui cessano tutti gli esterni impedimenti. Il che si può maggiormente ancora confermare: perchè, oltre a quel che si è detto, non par che alcun mobile possa aver  repugnanza ad un movimento senz’aver propension naturale all’opposto (perchè nella indifferenza non è repugnanza); e perciò chi volesse por nel Sole renitenza al moto circolare del suo ambiente, pur vi porrebbe natural propensione al moto circolare opposto a quel dell’ambiente; il che mal consuona ad intelletto ben temperato.
Dovendosi, dunque, in ogni modo por nel Sole l’apparente conversione delle macchie, meglio è porvela naturale, e non per participazione, per la prima ragione da me addotta.

In definitiva Galileo assegnava al Sole un moto naturale poiché non vi era alcun impedimento e, con il Sole si doveva muovere ogni cosa che fosse in contatto con esso. Il Sole è corpo solido ed il suo muoversi su se stesso non è impedito da alcuna repugnanza e men che meno vi sono impedimenti esterni, tanto che il suo essere immobile o dotato di tale moto è del tutto indifferente. Il tutto va come una nave che, in mancanza di impedimenti, se gli venisse data una spinta in un mare tranquillo, continuerebbe  a girare intorno al globo, allo stesso modo che se lasciata in quiete vi resterebbe indefinitamente. Inoltre tale moto viene avvertito solo da uno che guarda da un luogo dove non vi sia lo stesso moto. E qui, il discorso della nave è quello che con maggiore successiva precisazione diventerà l’inerzia mentre questo richiamo all’avvertire il moto solo da differenti riferimenti è una prima enunciazione del principio di relatività.

(5) Federico Cesi dà cenno di aver ricevuto richiesta d’iscrizione per Baliani in una lettera a Galileo del 14 giugno 1614. Nella stessa lettera si parla della scomparsa di Filippo Salviati. Altra lettera di Cesi a Galileo del 12 luglio 1614 chiede a Galileo referenze su Baliani (nella stessa lettera Cesi comunica a Galileo la morte di Welser).

(6) Prima dello scambio epistolare del quale parlerò nel paragrafo seguente, vanno registrate due lettere di Baliani a don Benedetto Castelli, la prima del 20 febbraio 1627 in cui si occupava del moto di gravi per il quale sembrava aver trovato una certa legge (i corpi di moto naturale vanno aumentando le velocità loro con la proporzione di 1,3,5,7.., e così in infinito) che non era la stessa per i corpi liquidi e la seconda del 28 maggio 1627 che in minima parte trattava ancora delle medesime questioni.

(7) Il sifone in su è da noi utilizzato, ad esempio, nei travasi di liquidi, come mostrato in figura:

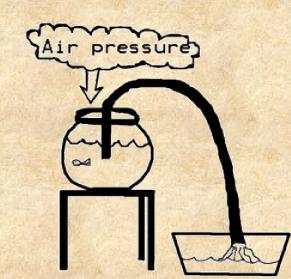
(8) E’ utile una considerazione. Siamo di fronte ad un esempio in cui la tecnologia pone un problema per la soluzione del quale occorre intervenire teoricamente con la scienza.

(9) Più tardi, nei Discorsi intorno a Due Nuove Scienze del 1638, su quest’argomento Galileo aggiungeva:

E perché la medesima altezza delle diciotto braccia è il prefisso termine dell’altezza alla quale qualsivoglia quantità d’acqua, siano cioè le trombe larghissime o strette o strettissime quanto un fil di paglia, può sostentarsi, tutta volta che noi peseremo l’acqua contenuta in diciotto braccia di cannone, sia largo e stretto, aremo il valore della resistenza del vacuo….

(10)  La prova che Torricelli avesse anche letto le lettere di Baliani a Galileo risiede nel fatto che alcuni dei motivi trattati in queste lettere vengono riecheggiati nelle Lezioni Accademiche (pubblicate postume nel 1715), che lo stesso Torricelli tenne presso l’accademia della Crusca (Io … fantasticava con l’immaginazione e mi dipingeva sopra la testa un altissimo pelago d’argento vivo. Ecco, io sono nato e allevato nel fondo di questo fluido metallo …) oltre ché in alcune lettere che Torricelli inviò a Michelangelo Ricci nel giugno del 1644, come ho già scritto nell’articolo Torricelli, il “peso” dell’aria ed il vuoto.

(11) Di grande importanza fu la pubblicazione nel 1644 dell’Opera Geometrica di Torricelli il cui titolo completo era: De sphaera et solidis sphaeralibus. De motu gravium naturaliter descendentium etc. De dimensione Parabolae solidique hyperbolici cum, appendice de Dimensione spatii cycloidalis et Cochleae. La seconda parte di tale lavoro, il De motu gravium, trattava ancora il moto dei gravi dando maggiore generalità e completezza matematica alla teoria del moto di Galileo ed aveva un’appendice che anticipava di due anni i lavori di Baliani con il titolo De motu acquarum in cui la teoria del moto veniva estesa ai liquidi. La trattazione di Torricelli del moto era molto articolata. Egli aveva stabilito molti teoremi riguardanti la caduta di gravi lungo piani inclinati differenti, corde di cerchio ed archi di parabola, arrivando anche a trovare che i tempi di discesa dei gravi lungo piani inclinati con la medesima altezza sono proporzionali alle rispettive loro lunghezze. Da notare che Torricelli, nella sua trattazione del moto, mette al centro della sua attenzione il concetto di momento, collegando strettamente le proprietà del moto alla gravità dei corpi grazie al concetto suddetto e quello di impeto (stessa cosa farà Baliani due anni dopo). Insomma vi è un cambiamento di prospettiva che fa passare da una trattazione puramente geometrica e cinematica che risponde alla domanda del come avviene il moto ad una che cerca di capire da cosa dipende il moto. Aveva inoltre trattato del moto dei proiettili estendendo la trattazione galileiana, relativa a proiettili sparati orizzontalmente, a proiettili sparati a differenti angolazioni. La parte relativa al moto del lavoro di Torricelli era già scritta nel 1641, con Galileo ancora in vita. Fu proprio attraverso questo lavoro che Benedetto Castelli fece conoscere Torricelli a Galileo nel 1641. Sappiamo di ciò da una lettera che Benedetto Castelli scrisse a Galileo il 2 Marzo 1641. L’abate Castelli era stato autorizzato a recarsi presso Galileo, in domicilio coatto ad Arcetri e nel comunicare a Galileo di aver avuto il permesso aggiunse che gli avrebbe portato un libro, e forsi ancora il secondo libro, fatto da un mio discepolo […] che ha dimostrato molte proposizioni di quelle De Motu dimostrate già da V.S., ma diversamente superedificando maravigliosamente intorno alla stessa materia[…].

La parte relativa ai liquidi dell’Opera Geometrica era invece un’assoluta novità tanto che Torricelli è noto come il fondatore dell’idrodinamica. Studiò, in particolare, sia con elaborazioni teoriche che con esperienze, l’efflusso di liquidi da fori praticati in differenti recipienti arrivando a determinare quella che è oggi nota come la legge di Torricelli:  l’acqua che erompe violentemente ha nel punto d’efflusso la stessa velocità che avrebbe un qualunque corpo grave, ossia anche una singola goccia della stessa acqua, che fosse caduta naturalmente dal livello supremo della stessa acqua sino all’orificio d’efflusso. Inoltre stabilì che Le quantità di acqua che scorrono in tempi uguali attraverso un foro praticato alla base di un recipiente stanno fra loro come le radici quadrate delle altezze del liquido in esso contenuto. Per la prima volta, veniva collegata la portata che esce da un foro in un recipiente e la radice quadrata dell’altezza del livello dell’acqua, nel recipiente stesso, oggi chiamata carico idraulico o battente (purtroppo non si era ancora pronti ad inserire una dipendenza dall’accelerazione di gravità che invece gioca un ruolo importante). E poiché la √h risulta proporzionale alla velocità V, sarà anche h proporzionale alla velocità al quadrato V² , scoperta fondamentale che cento anni dopo sarà la base da cui partiranno Daniel Bernoulli e Lehonard Euler per le loro ricerche di idrodinamica.

(12) Consiglio qui, per comprendere a cosa si riferisce Baliani, di andare a leggere il contenuto dei Discorsi nell’aricolo Gli ultimi anni di Galileo.

(13) Ricordo che quando Galileo provava a consigliare Baliani per la costruzione del sifone, paragonava la salita dell’acqua nelle tubature ad un qualcosa che dovesse essere tirato su da funi.

(14) Baliani fa riferimento al tema che Galileo tratta utilizzando la seguente figura alla quale vanno riferite le lettere utilizzate nella lettera. Per vedere questo tema come è stato trattato da Galileo occorre andare alle pagine 23-26 dell’articolo citato in nota 12.

(15) Galileo si riferiva ad un suo lavoro iniziato nel 1637 dal titolo Le operazioni astronomiche. Esso, nelle intenzioni di Galileo, doveva far parte della Quinta Giornata, mai realizzata, dei suoi Discorsi. Questo testo rimase tra le carte ereditate dal figlio di Galileo ed ora si può leggere nell’Edizione Nazionale delle Opere di Galileo, Vol. VIII, pagg. 453-466.

(16) Scrive in proposito la Baroncelli:

Le edizioni del De motu del 1638 che sono riuscita a consultare (British Library, Biblioteca Vaticana, Bibliothèque Nationale di Parigi, Biblioteca Universitaria di Genova, Biblioteca dell’Istituto e Museo di Storia della Scienza di Firenze) non recano traccia delle correzioni annunciate. Tuttavia ad esse si può risalire facilmente. La descrizione inviata a Galileo collima infatti con la stesura lievemente diversa del Libro I del 1646; una lettera inviata a Giannantonio Rocca il 26 ottobre 1639 chiarisce inoltre per intero la vicenda di queste varianti, niente affatto legate, come l’autore voleva far credere, a fortuiti errori di stampa. Era stato l’ amico e discepolo del Cavalieri, infatti, a segnalare a Baliani l’esistenza di una contraddizione che, agendo a livello dei fondamenti, minava per intero la struttura dell’opuscolo; né il Baliani aveva saputo dare alla difficoltà una convincente soluzione.
La risposta di Galileo, se ci fu, è andata perduta. È sintomatico, però, che a partire da questo momento cessi ogni scambio epistolare tra i due scienziati. Sicuramente a questo periodo risale la scrittura galileiana fortemente critica nei confronti dei fondamenti de motu del Baliani pubblicata dal Caverni [Caverni, Storia del metodo sperimentale in Italia, tomo IV, Firenze, Civelli, 1895, pp. 313-314]. Tali osservazioni furono dettate da Galileo a Vincenzio Viviani, il giovane assistente dei suoi ultimi anni di Arcetri, lo stesso che aveva raccolto e stilato, dopo la pubblicazione dei Discorsi, la dimostrazione dell’uguaglianza dei gradi di velocità a pari distanze verticali dalla quiete. Non è improbabile che Galileo abbia agitato nei confronti del troppo disinvolto scienziato genovese la minaccia di una sua risposta pubblica, e ben circostanziata, questa volta, se questi avesse persistito nelle sue pretese. Certo è che la scrittura galileiana segnala un dissenso teorico ben più forte di quello emergente dalle lettere precedentemente inviate al Baliani («voi prendete come chiara notizia accidenti i quali niuna connessione hanno con moti fatti sopra linee non rette») e ha il timbro e la decisione che si usano nei confronti di un avversario, al quale puntigliosamente si obietta un elenco di «supposizioni assai dure» e una ulteriore «disparità massima». Sta di fatto che il Baliani abbandonò, al momento, ogni velleità di ampliamento o completamento del trattato; contemporaneamente si infittivano i suoi contatti e lo scambio epistolare con il Confalonieri, il Grassi e Mersenne. Qualche anno più tardi, però, quando Galileo non aveva più voce e la sua teoria de motu era l’oggetto di un ripetuto e ben organizzato attacco, e nel momento in cui dalla sua opera prendeva le distanze anche Mersenne, scettico circa la saldezza delle parziali conquiste galileiane, sempre più pressantemente criticate dalla ben più organica filosofia di Descartes, poteva aver luogo la resa dei conti.
Il primo attacco, violentissimo, fu quello del gesuita Niccolò Cabeo, che nei Commenti alle Meteore del 1646 prese le difese del Baliani, primo vero scopritore della legge di caduta dei gravi. Sempre nel 1646 compariva il ben più vasto De motu del Baliani, riproponendo molti dei teoremi più importanti dei Discorsi in chiave fortemente diversa da quella galileiana, e una legge di caduta singolarmente concorde nelle motivazioni come nei risultati con quella proposta dal gesuita Onorato Fabri. Infine fu il Baliani stesso a sottolineare seccamente a Mersenne la propria distanza da Galileo: perché un conto era la convergenza dei risultati, un altro l’identificazione del percorso. Egli aveva provato prima di Galileo e indipendentemente da lui la legge di caduta, e ne chiamava a testimone il padre Cabeo, citando proprio le rozze pagine sopra ricordate delle Meteore.
L’asserzione è chiaramente falsa. La prima notizia certa è desumibile da una lettera del 1627 a Benedetto Castelli: «mi riuscì a parer mio ben dimostrata una propositione per una via molto stravagante, la quale già il signor Galileo mi haveva detta per vera, senza però addurrnene la dimostratione; et è che i corpi di moto naturale vanno augumentando la velocità loro con la proportione di 1,3,5,7, e così in infinito. Me ne addusse però una ragion probabile […] Però io l’ho dimostrata con principij molto diversi» [Baliani a Castelli, 20 febbraio 1627].
Quanto ai principi e al metodo, essi erano toto caelo diversi da quelli di Galileo, e del principio comune, il suo Postulato VII, egli possedeva e forniva ora la dimostrazione nel Libro II. Si riconosceva ammiratore di Galileo, ma in nessun modo un suo seguace.
La considerazione amara circa lo spessore di un uomo che fino a pochi anni prima aveva professato di «seguire le pedate» di Galileo e ora, mutato il clima, non esitava a prenderne accuratamente le distanze ha qui scarso interesse, e soprattutto non basta a spiegare una divaricazione che ha radici, almeno in parte, nella diversa concezione dei criteri normativi e metodologici della fisica, ribadita con izza, anche se tardivamente, a Mersenne.
Osserveremo come chiari segni dell’ eredità galileiana fossero mescolati a simmetriche contrapposizioni e a procedure del tutto estranee già nella prima edizione del De motu, e come queste differenze si andassero accentuando per l’intervento di suggestioni diverse nella seconda edizione. In questa emblematica vicenda, nella quale la stima e le discussioni di un ventennio si consumano e si concludono con un dissidio personale, le divergenze teoriche procedono parallelamente, accentuandosi e sfociando infine in un aperto contrasto. Trascurare questa evoluzione significa precludersi, in parte, anche la comprensione dell’opera scientifica di Giovannni Battista Baliani. […].

(17) “Del concetto di momento il Baliani discusse a più riprese con il gesuita Giovanni Luigi Gonfalonieri [al  quale accennerò più oltre nel testo, ndr], che gli obiettava la scarsa perspicuità della definizione data nel De motu. In effetti, definendo il momento come differenza tra gravita e resistenza offerta dalla materia al moto, il Baliani sembrava trascurare il fatto che il concetto da lui coniato non era in alcun modo identificabile con quello di peso x braccio o peso x velocità che interveniva nei teoremi classici della leva e del piano inclinato; e che, in secondo luogo, volendo davvero definire una sorta di ‘forza specifica’ indipendente dalla massa del grave, avrebbe dovuto ricorrere ad un rapporto, non solo ad una differenza. Baliani infine ammise con l’amico di essere stato «scarzo nelle parole in dichiararlo», pur ribadendo che nel suo intendimento il concetto significava appunto il rapporto tra la forza efficace e la resistenza materiale del grave”.

(18) “Tale velocità deve essere intesa, ovviamente, come una velocità media. Il Baliani tuttavia non lo specifica né, d’altro canto, la proposizione reggerebbe ad una tale interpretazione, dovendo risultare appunto le due velocità medie uguali. Ipotizzando che il Baliani intenda parlare di velocità media per l’inclinata e la perpendicolare, l’enunciato diventerebbe vero con una ulteriore precisazione: ammettendo cioè di considerare l’intera perpendicolare AB e la porzione di inclinata percorsa in un tempo uguale, ciò che però il Baliani assolutamente non dice qui: è quanto farà, glissando con incredibile disinvoltura sull’enunciato, nel 1646, quando si vedrà costretto ad ammettere l’infinito variare della velocità nel moto di caduta. La proposizione risulterebbe vera anche ammettendo che per velocità Baliani intenda le velocità istantanee raggiunte sulla perpendicolare e sull’inclinata dopo tempi uguali […] ma lo scienziato parla qui di «velocitas super AB» e «super AC». Questi punti verranno presi in considerazione nelle pagine seguenti”.

(19) Le conclusioni che trae la Baroncelli sul De motu del 1638 sono una vera stroncatura del lavoro di Baliani:

“Ma né le obiezioni del Confalonieri, né quelle del Cavalieri sortirono l’effetto di incrinare la fiducia dello scienziato nella proporzionalità tra momenti e velocità, o nel suo diretto corollario, la proposizione XI, che stabilisce l’inversa proporzionalità tra la ‘velocità’ dei gravi lungo l’obliqua e la perpendicolare di un piano inclinato e le linee stesse.
È significativo che la proposizione XI venga richiamata in tutto il libro solo quattro volte, e in tutti i casi in modo improprio: in tutte e quattro le occorrenze viene citata come se affermasse la diretta proporzionalità tra i tempi necessari a percorrere inclinata e perpendicolare e le linee stesse. Evidentemente il Baliani riteneva i due enunciati pienamente equivalenti, persuaso che le velocità di due moti siano comunque inversamente proporzionali ai tempi, e inconsapevole di aggiungere alla già discutibile costanza delle velocità l’ulteriore errore di applicare una proprietà del moto uniforme, ma valida solo a parità di spazi percorsi, ad un caso in cui gli spazi sono evidentemente diversi. Non solo: dopo aver usato in questo modo distorto la proposizione XI per stabilire alcuni tra i teoremi più importanti del libro, sentiva la necessità, giunto alla fine, di dimostrare proprio quell’assunto.
Le incongruenze strutturali del libro, i fraintendimenti e gli errori delle citazioni, nonché l’ambiguità della proposizione XI non sfuggirono all’esame acuto e diligente del Rocca. Questi, letto il libro, fece subito pervenire all’autore le proprie osservazioni tramite il genovese Giacomo Vezzani. La risposta immediata e circostanziata del Baliani, i replicati ringraziamenti, le giustificazioni addotte, l’annuncio della ristampa di alcune proposizioni esprimono senza possibilità di equivoco l’imbarazzo dello studioso di fronte alla contraddizione così facilmente messa a nudo persino da un oscuro ‘dilettante’. Il Rocca obiettava che il rapporto tra i tempi per la perpendicolare e l’inclinata richiesto nel corso della dimostrazione della proposizione XIV non poteva essere fornito dall’enunciato della proposizione XI, che dava solo il rapporto delle relative velocità; anzi, l’enunciato della proposizione XIV – che determina lo spazio sull’obliqua percorso nello stesso tempo impiegato nella caduta verticale era contraddittorio rispetto a quello della proposizione XI. Una volta supposto il rapporto tra le velocità inverso di quello delle linee dei piani, infatti, si dimostrava facilmente che il tempo per la perpendicolare e quello impiegato a percorrere la sua proiezione sull’ inclinata non potevano essere uguali. Per giustificarsi il Baliani adduceva, prima, uno scambio fortuito nella numerazione delle proposizioni XI e XXII; poi, alle strette, affrontava more geometrico la questione sollevata dal Rocca, cercando di dimostrare nuovamente la proposizione XIV. Non ammise esplicitamente la falsità del rapporto tra le velocità: non poteva, o sarebbe saltato, insieme alla proporzione momenti-velocità, l’intero fondamento del libro. Preferì glissare, concedendo soltanto che il rapporto tra le velocità cadeva nel caso prospettato («hoc non sequitur in moto accelerato») per privilegiare, tra i due, l’enunciato davvero essenziale della proposizione XIV.
In questo nuovo tentativo di dimostrazione, tuttavia, il Baliani certamente comprese che non poteva in alcun modo prescindere dalla variazione istantanea della velocità in uno stesso moto di caduta; e che, se proprio voleva mantenere la costanza del rapporto tra momenti e velocità su piani diversamente inclinati, doveva escogitare l’artificio verbale, inconfessabile perché a rigore inammissibile, di riferirsi alla velocità non per l’intera obliqua ma per la proiezione della perpendicolare sull’obliqua, cioè dopo tempi uguali. È quanto intendeva fare nelle correzioni annunciate agli amici nel 1639 e quanto farà in effetti nella seconda edizione del Libro I, senza avvertire però il lettore, neppure con una frase, che le velocità coinvolte erano, questa volta, velocità istantanee.
La pubblicazione del De motu del 1638 si concludeva perciò con uno scacco. Solo grazie ad un lessico ambiguo, ad occultamenti consapevoli e a inammissibili incongruenze deduttive il Baliani era riuscito a stabilire o, per dir meglio, a far galleggiare fortunosamente un discreto gruppo di teoremi sul moto di caduta quasi tutti concordi con quelli anche oggi ritenuti ‘canonici’, nei quali non c’è traccia di alcuna crescita o proporzionalità della velocità né allo spazio, né al tempo, né ad alcuna altra grandezza se non al momento, e nella quasi totalità dei quali il concetto di velocità è del tutto assente. E se da un lato il concetto di momento, opportunamente riformulato, si rivelava di grande efficacia a spiegare l’uguaglianza delle cadute di gravi di massa diversa e il variare dell’ accelerazione con l’inclinazione del piano, quello stesso concetto però non rendeva conto adeguatamente della velocità di uno stesso moto: anzi le contraddizioni si annidavano proprio là dove lo sforzo innovativo del Baliani era stato più intenso, nel legame coraggiosamente stabilito tra momenti e velocità .
Proprio per questo motivo, e non perché mancasse di evidenza, lo scienziato aveva emarginato dal gruppo degli altri e confinato al termine del libro il Postulato VII, che richiede infatti il concetto di grado di velocità; che cosa poi fossero gli uguali «gradi di velocità» posseduti dai gravi a uguali distanze verticali dalla quiete il Baliani non spiegava, rifugiandosi nell’ancor più oscuro vocabolo di uguaglianza dei «motus in fine» e nella rassicurante specificazione che si trattava pur sempre di velocità uniformi, giacché se i gravi «ab inde infra sortiantur parem inclinationem, aequeveelociter moventur». Dal Postulato VII, così, non faceva dipendere alcuna proposizione fondamentale del trattato; deliberatamente l’aveva posposto, a causa della sua oscurità, diceva; in realtà doveva trovarlo molto dubbio, se non addirittura contraddittorio con l’asserzione della inversa proporzionalità tra le velocità per l’inclinata e la perpendicolare e le linee stesse. Esso serviva solo a stabilire che la caduta lungo le corde di un semicerchio si verifica in minore «diuturnitas» di quella lungo il diametro verticale. La sua emarginazione testimonia tuttavia la resistenza dello scienziato a definire, nonché ad usare, il concetto di velocità istantanea; un concetto che, diventato necessario e urgente, verrà nel Libro II del 1646 surrogato e giutificato da quello più consueto, e causale. di «impetus»”.

(20) Questo punto viene così discusso dalla Baroncelli:

Ben lungi dal definire il moto accelerato con una legge che stabilisca la variazione della velocità. il Baliani utilizza la legge spazio-temporale di caduta per confrontare gli spazi percorsi in due intervalli temporali uguali e consecutivi alla quiete dello stesso moto e individuarne due componenti: la prima, dovuta alla gravità; la seconda, dovuta ad un agente indotto dal «primo movimento», cioè all’impeto prodotto nel primo intervallo di tempo. Se infatti nel secondo intervallo di tempo agisse ancora e soltanto la gravità – argomenta il Baliani – il secondo spazio non potrebbe che essere uguale al primo, dal momento che «pares causae producunt pares effectus»; poiché, al contrario, tale spazio è triplo del primo, occorre che i suoi 2/3 siano causati dall’impeto. Il solo impeto, dunque, «sine ope gravitatis», è capace di far percorrere al mobile nel secondo intervallo temporale uno spazio doppio di quello percorso per 1’azione della gravità nel primo intervallo. L’assioma così plausibile secondo cui la stessa causa non può che produrre lo stesso effetto sta qui a sottintendere la certezza che una forza costante non possa produrre che un movimento uniforme: anche a movimento iniziato, dopo un intervallo di tempo finito, il moto dovuto alla «gravitas» è assimilabile ad un ‘urto’ identico a quello comunicato a partire dalla quiete. In sostanza, secondo il Baliani un moto è uniforme non quando non è soggetto a forze, bensì quando è soggetto ad una forza costante. Tanto è vero che il moto accelerato può essere spiegato solo introducendo un ‘motore’ aggiuntivo, l’impeto. Più che ad una vera e propria dimostrazione, siamo di fronte ad un tentativo di spiegazione causale del moto di caduta – interamente ricondotto all’azione della gravità, è vero – e ad una delucidazione delle sue due componenti, entrambe uniformi: perché anche l’impetus, considerato di per sé, genera un movimento uniforme, come è dimostrato nelle proposizioni II e III.
L’accelerazione viene così relegata ancora una volta ad effetto collaterale della gravità, respinta più in fondo, ma non spiegata: perché mai la gravità dovrebbe produrre, oltre alla velocità e al primo movimento, anche l’impeto? Lo studioso risponderà più tardi, nel libro IV, appellandosi alla spiegazione metafisica delle forme sostanziali. Come la materia costituisce un principio essenziale di passività e resistenza al movimento, anche a moto iniziato, così l’impeto è connaturato alla sostanza del mobile per conferirgli, in quanto mobile, la proprietà di conservare e perpetuare il movimento, in una sorta di duplice principio inerziale. Curiosa «propensio ad motum», duale della passività della materia, questa caratteristica dovrebbe inerire anche al corpo in quiete, essendo l’impeto una forma sostanziale del mobile: e infatti vi si trova, ma «in actu primo», mentre in quello in movimento si trova «in [actum] secundum».
Nel primo intervallo temporale, perciò, la sola gravità, o il suo momento, conferisce al grave una determinata velocità, indipendente dalla massa e in assenza di ogni impeto; da quel momento in poi gravità e impeto indotto dal primo movimento agiscono insieme, sommandosi. La caduta viene così percepita come un movimento nel quale l’accelerazione si produce a scatti, e la velocità cambia dopo intervalli finiti: osservato da vicino, cioè in un intervallo temporale sufficientemente piccolo, il movimento accelerato manifesta solo le caratteristiche di un moto uniforme, perché sostanzialmente riducibile ad una sommatoria di moti uniformi. Il galileiano triangolo tempo-velocità, se mai il Baliani avesse utilizzato uno schema analogo, risulterebbe qui una figura denticolata costituita da rettangoli, nella quale la componente spaziale prodotta dalla gravità è costante, così com’è «aequabilis» il «motus ab impetu proveniens».

[…]

Sarà opportuno … leggere con particolare attenzione, alla luce delle precedenti considerazioni, l’introduzione al Libro IV, nella quale lo studioso fa la storia e il riepilogo conclusivo della propria riflessione sul movimento. È inevitabile anche chiedersi perché egli affronti solo ora un argomento che avrebbe potuto trovare un luogo più appropriato nei libri precedenti. Il motivo – risponde il Baliani – risiede nel fatto che tali considerazioni non attengono propriamente alla ricerca fisica, bensì al livello superiore, filosofico e metafisico, della indagine delle cause; e sebbene tale livello sia più appagante, è al tempo stesso più incerto, e non va in alcun modo mescolato con l’indagine fisica. Questa parte da dati osservativi e da postulati di indubbia evidenza; quella, per sua natura, non può mai uscire dal dominio della probabilità, e ciò nonostante esercita una istintiva, irreprimibile attrattiva intellettuale. Anch’egli aveva ceduto a quell’impulso nella prefazione al Libro I, spiega il Baliani, che ha bisogno di ridimensionare il rilievo dato lì al concetto di momento, salvando al tempo stesso le conclusioni, senza di cui la parte successiva non si reggerebbe; là aveva rintracciato il motivo della caduta identica di gravi di massa diversa nella crescita proporzionale di gravità-resistenza materiale, ovvero nell’uguaglianza dei momenti: «non tamen ex hoc ego me adhuc gravium naturam omnino assecutum esse pro certo habeo». Una ulteriore riflessione sulla causadell’ accelerazione lo aveva infatti condotto al concetto di impeto causato dalla gravità: un concetto importante ma che sembrava in un primo momento incapace di fornire quantitativamente la misura dell’accelerazione e, in un secondo momento, addirittura contraddittorio rispetto alla legge di caduta già dimostrata. Restava inspiegato, infatti, il motivo per cui lo spazio percorso nel secondo intervallo temporale fosse triplo del primo, a meno di ammettere che l’impeto fosse maggiore della propria stessa causa. La successiva scoperta che l’impeto produce un moto uniforme poteva rivelarsi la chiave per comprendere le caratteristiche di ogni movimento, e anzi l’essenza stessa del movimento: suggeriva che la natura del mobile consistesse proprio nell’indifferenza alla quiete e al movimento, e spiegava il fatto che, una volta in moto, il mobile persistesse in tale stato con la stessa velocità finché non gli si opponesse qualche resistenza. L’impeto veniva così definito come la potenzialità insita nel mobile di conservare il moto, una volta che questo fosse stato effettivamente prodotto da una forza attiva. Ora lo scienziato ribadisce più volte che l’impeto non è prodotto direttamente dall’ agente: la presenza di un «motore» produce non l’impeto ma un «primo movimento» dal quale l’impeto è assente, e tale movimento porta dalla potenza all’ atto, quasi risveglia l’ impeto che, persistendo anche in assenza del motore, è responsabile del successivo moto uniforme.
La concatenazione causale tanto insistentemente ribadita risponde a due precise istanze. In primo luogo, se la gravità producesse l’impeto, rimarrebbe inspiegata l’accelerazione, oppure occorrerebbe ammettere che l’impeto è causa di se stesso, con il conseguente risorgere delle tante difficoltà ben note ai seguaci della celebre teoria medievale. In secondo luogo, ogni corpo conterrebbe nella propria natura ed essenza due principi contrapposti: la materia, che si oppone al movimento, come Baliani ha già asserito e, contemporaneamente, l’impeto, che promuove e conserva il movimento. Per sfuggire a questa antinomia allo scienziato non resta che presupporre un ‘primo movimento’ determinato dal rapporto tra gravitas e materia – e dal quale è assente l’impeto – al termine del quale scaturisce il primo impeto.

[…]

Quanto alla discrepanza tra la legge galileiana degli spazi crescenti come la successione dei numeri dispari, già da lui condivisa e dimostrata, e quella della successione naturale, qui nuovamente proposta, Baliani risponde sorprendentemente che, a rigore, la legge galileiana è falsa; ciononostante la discrepanza tra le due leggi tende a zero perché, riducendo nella seconda lo spazio e il tempo iniziali in cui si produce il primo impeto, si ottengono approssimazioni sempre più vicine alla legge galileiana. Ecco un esempio in cui un criterio puramente osservativo risulta insufficiente a dirimere la verità di un enunciato.
La conclusione è sorprendente, e ancor più il ribaltamento della posizione metodologica fin qui sostenuta: Galileo ha sbagliato perché si è fidato delle osservazioni e ha fondato la propria legge unicamente su basi sperimentali. Tuttavia sarebbe ingeneroso fargli una colpa per non aver riconosciuto e distinto differenze insensibili. I sensi sono soggetti all’ errore, le indicazioni dell’ esperienza – le uniche attendibili nell’ indagine fisica, aveva sostenuto fin qui – non riescono ad oltrepassare la grossolana soglia ella percezione; il ragionamento sui principi, al contrario, conduce a conclusioni rigorose, quali questa nuova legge di caduta, sicuramente corretta perché confortata anche dall’evidenza sperimentale.
Forse proprio perché non lo nomina mai, la pagina evoca vivamente l’opera di Galileo, e al tempo stesso trasmette al lettore un’esortazione dolciastra e magnanima alla tolleranza nei confronti del suo errore: questa volta, l’intera teoria de motu. Galileo ha costruito solo una cinematica, e attorno ad una legge desunta unicamente da dati osservativi. Ora che tale legge vacilla, si rivela fittizio anche il complesso di ipotesi escogitato per giustificarla. Le infinite velocità crescenti istante per istante possono essere spazzate via come inutili e arbitrarie; il movimento accelerato si rivela una composizione di moti uniformi in cui la velocità varia, ma non con continuità. Ogni necessità di considerazione dell’infinito e dell’ indivisibile è tolta: bastano spazi piccoli e finiti, tempi atomi ma quanti, e velocità uniformi. E se l’errore teorico è da scusare, molto meno giustificabile e condivisibile appare l’etica scientifica di Galileo, al quale lo scienziato direttamente rimprovera eccessiva presunzione, imprudenza intellettuale e mancanza di relativismo nei confronti delle proprie scoperte.

(21) Le citazioni provengono dall’articolo di Moscovici. La traduzione di tali citazioni, fatte in francese, è mia.

BIBLIOGRAFIA

(1) Giovanni Battista Baliani – De motu naturali gravium solidorum et liquidorum (a cura di Giovanna Baroncelli) – Giunti 1998

(2) Claudio Costantini – Baliani e i Gesuiti – Giunti 1969

(3) Lucio Russo – Flussi e riflussi – Feltrinelli – Feltrinelli 2003

(4) Umberto Forti – Storia della scienza – dall’Oglio 1968

(5) Juan Vailati – Contribución a la historia de la mecánica – Espasa-Calpe, Buenos Aires 1947

(6) Andrea Lavaggi – Attività e propensioni scientifiche in Liguria nei secoli XVI E XVII – Balbisei. Ricerche Storiche Genovesi, n. 1 (2004)

(7) Galileo Galilei – Le opere – Edizione Nazionale, Giunti Barbera, 1968.

(8) Michele Camerota – Galileo Galilei – Salerno 2004

(9) Paolo Galluzzi – Gassendi and l’Affaire Galilée of the Laws of Motion – Cambridge Journals on line, 1993

(10) Serge Moscovici – Le développements historiques de la théorie galiléenne des marées – Revue d’histoire des sciences et de leurs applications, 1965
 

Categorie:Senza categoria