Roberto Renzetti

PREMESSA

    Ci troviamo ad un momento della fisica di fine Ottocento in cui si intersecano i lavori di vari fisici. Molti ed in molti ambienti scientifici, in particolare nella Vienna austro-ungarica, affrontano problemi che si fanno impellenti e che emergono da varie indagini scientifiche. Tra questi problemi emerge quello che era stato posto all’attenzione della fisica da Kirchhoff, il corpo nero.

    Ritroviamo qui un grande della fisica del quale mi sono occupato, Ludwig Boltzmann e, nel seguito, sempre più spesso vi saranno scienziati che opereranno in campi diversi e che dovrò trattare in ambiti diversi.

    In questo lavoro inizierò a trattare la biografia scientifica di Joseph Stefan che, ricorderà chi ha letto la biografia di Boltzmann, era stato uno dei docenti di quest’ultimo. Dalla collaborazione tra i due nacque quella che è oggi nota come la legge di Stefan-Boltzmannn. Come proseguimento ideale di questo lavoro vi sono le ricerche di Wien e quindi le sue leggi (la generale, dello spostamento e dell’irraggiamento) ed ancora i lavori di Raileigh-Jeans (dei quali mi occuperò in un successivo lavoro). 

BIOGRAFIA SCIENTIFICA DI JOSEPH STEFAN

    Joseph Stefan nacque nel 1835 a Sankt Peter, un villaggio della Slovenia nell’Impero austro-ungarico da genitori umili, analfabeti e non sposati. Suo padre, Ales, era mugnaio e panettiere mentre sua madre, Marija Startinik, era cameriera.

    Joseph fece le scuole elementari a Klagenfurt dove si distinse tanto che ai genitori fu consigliato il proseguimento degli studi nel ginnasio della stessa città dove entrò nel 1845. I moti rivoluzionari del 1848 lo colpirono in modo particolare anche se aveva solo 13 anni e tracce di ciò le troviamo nella sua futura produzione letteraria in sloveno che sarà di una qualche importanza. Alla fine del ginnasio fu tentato per un poco di diventare monaco benedettino ma la fisica poté di più e, nel 1853, passò a studiare matematica e fisica all’Università di Vienna dove si laureò nel 1857. Iniziò ad insegnare fisica agli studenti di farmacia, quindi lavorò all’Istituto di Fisiologia, finché nel 1863, dopo essersi abilitato nel 1858, passò ad insegnare fisica all’Istituto di Fisica dell’Università di Vienna, nell’Istituto fondato da Doppler nel 1850. e da dove ebbe inizio la sua brillante carriera accademica piena di riconoscimenti ed onori da varie istituzioni scientifiche europee.

    Il suo primo importante lavoro sperimentale, Untersuchung über die Wärmeleitung in Gasen, Erste Abhandlung, (Ricerche sulla conducibilità termica nei gas, parte prima; Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Math.-Natur. Abt. 2, 65: 45-69; 1872), riguardò la conducibilità termica dei gas a partire da alcune questioni sollevate sull’argomento da Maxwell, del quale era grande ammiratore e divulgatore, nella sua memoria Illustrations of the Dynamical Theory of Gases  (Philosophical Magazine 19; 19-32, 1860; 20; 21-37, 1860) e nella successiva Untersuchung über die Wärmeleitung in Gasen, Zweite Abhandlung (Ricerche sulla conducibilità termica nei gas, parte seconda; Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Math.-Natur. Abt.2, 72: 69-101; 1875). Le misure fatte da Stefan e per le quali realizzò un ingegnosissimo apparato, il diatermometro, erano estremamente complesse tanto che lo stesso Maxwell aveva sostenuto: Dovrebbe essere quasi impossibile stabilire il valore della conducibilità termica di un gas da esperimenti diretti, poiché il calore radiato dalle pareti del contenitore dovrebbe essere molto più grande del calore trasportato attraverso l’aria, e ciò anche se si riuscissero ad eliminare completamente le correnti. Il diatermometro di Stefan prevedeva la sistemazione del gas nel sottile spazio esistente tra due cilindri concentrici. Si faceva poi passare con rapidità del calore attraverso di esso e si riusciva a misurarne la conducibilità termica (con un errore, rispetto alle misure odierne, di solo il 10%). Boltzmann, allievo di Stefan, ebbe a dire che quello strumento era estremamente semplice e che con esso si ottenevano risultati prima impensabili e di grandissimo aiuto per le elaborazioni della teoria cinetica dei gas. Uno dei risultati che Stefan seppe trovare fu la verifica sperimentale di quanto avevano trovato Maxwell e Clausius e cioè l’indipendenza della conducibilità termica dalla pressione.

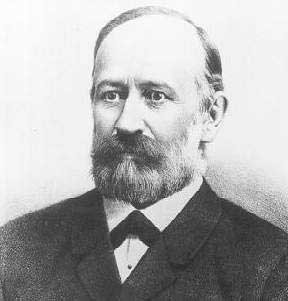
    Gli studi di Stefan si indirizzarono poi verso gli studi di Kirchhoff sul corpo nero che riassumo in breve.

    Era già noto che l’irraggiamento calorifico e quello invisibile (radiazione infrarossa) sono la stessa cosa. Kirchhoff nel 1859 mostrò che il rapporto tra potere emissivo (e) e potere assorbente (a) di un corpo, rispetto ad una radiazione di data frequenza, non dipende dalla natura del corpo né dalla sua forma, ma solo dalla temperatura, risultando constante per tutti i corpi che si trovano alla stessa temperatura. In definitiva questo rapporto è una funzione, da determinarsi, delle sole frequenza (ν) e temperatura (T), che chiameremo funzione di distribuzione (dell’intensità della radiazione):

(1)                                             

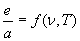
Egli definì poi come corpo nero un corpo che abbia potere assorbente uguale ad 1, un corpo cioè in grado di assorbire tutte le radiazioni che lo colpiscono (qualunque sia la loro frequenza) e, per la legge di inversione, di emetterle tutte. Trovò quindi che, essendo il potere assorbente di un corpo nero uguale ad 1, il suo potere emissivo è indipendente dalla natura e dalla forma della sostanza che lo costituisce, dipendendo solo dalla temperatura T a cui si trova il corpo nero e dalla frequenza ν della radiazione considerata. In formula, poiché a = 1, la (1) per un corpo nero diventa:

(2)                                             e = f (ν ,T)

a meno di una constante moltiplicativa. E’ opportuno osservare che l’importanza del corpo nero risiede nel fatto che, per esso, il potere emissivo risulta uguale alla  funzione di distribuzione della radiazione esistente al suo interno. Poiché la funzione di distribuzione è la grandezza che a noi interessa e non siamo in grado di misurarla, possiamo farlo misurando il potere emissivo.

    A partire da questo momento, come avevo detto parlando di Kirchhoff,  molti fisici di tutta Europa cercarono di determinare la funzione f (ν,T). Il fatto importante che Kirchhoff aveva determinato, l’indipendenza del potere emissivo di un corpo nero dalla natura del corpo medesimo, permetteva di lavorare su una ipotesi di materia che prescindesse dalla sua costituzione vera (peraltro all’epoca non conosciuta) e, ad esempio, di considerare la materia reale come un insieme di oscillatori armonici. Questi ultimi si sapevano trattare matematicamente e con essi era possibile ricondurre il problema della ricerca della funzione f (ν,T) ad un problema trattabile con i metodi e gli strumenti matematici della fisica teorica.

    Prima di andare oltre, è necessario definire un concetto connesso con la funzione f (ν,T). Se e = f (ν,T) è il potere emissivo del corpo nero (uguale alla funzione di distribuzione), la quantità:

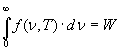
(3)  

                                       
rappresenta l’intensità totale della radiazione, poiché la quantità f (ν,T).dν rappresenta l’intensità della radiazione compresa tra νe ν + dν.
 

L’INTERVENTO DI STEFAN

    Il primo che fornì una formula che tentava di stabilire la natura della f (ν ,T)⁽¹⁾   fu appunto Stefan. Egli, da alcuni dati sperimentali di cui disponeva ed ottenuti dal fisico irlandese John Tyndall (1820 – 1893) nel 1865⁽²⁾, ricavò una formula empirica che metteva in relazione la densità (o energia per unità di volume) E⁽³⁾ della radiazione emessa da un corpo nero con la temperatura assoluta T cui si trovava il medesimo corpo nero. I risultati furono pubblicati in Über die Beziehung zwischen der Wärmestrahlung und der Temperatur (Sulla relazione esistente tra la radiazione termica e la temperatura, Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften, Bd. 79, S. 391-428; 1879) dove possiamo leggere:

Dal debole calor rosso (circa 525°C) al completo calor bianco (circa 1200°C) l’intensità della radiazione aumenta da 10,4 a 122, quasi 12 volte (più precisamente 11,7). Questa osservazione mi ha convinto a considerare il calore della radiazione come proporzionale alla quarta potenza della temperatura assoluta. Il rapporto delle due temperature assolute 273 + 1200 e 273 + 525 elevate alla quarta potenza fornisce 11,6.

    La E doveva quindi risultare proporzionale alla quarta potenza della temperatura assoluta, secondo la relazione:

(2)                                           E = k₁· T⁴

dove k₁ è una constante che può essere determinata sperimentalmente. Questa legge era in buon accordo con i dati a basse temperature ed era particolarmente accurata ad alte temperature.    

    Le conclusioni di Stefan erano certamente azzardate ed erano anche non usuali nel modo in cui erano state ricavate. Partiva da pochi dati sperimentali che non garantivano certamente la sua conclusione. In ogni caso Stefan⁽⁴⁾ applicò la sua legge per calcolare la temperatura del Sole che risultò essere quella che oggi accettiamo (circa 5500 °C) con un margine d’errore del solo 3%. Il risultato restò praticamente in sospeso fino a che nel 1884 il suo ex alunno Boltzmann non ne mostrò teoricamente la correttezza mediante il 2º principio della termodinamica, alcuni risultati di Maxwell (relativi alla pressione di radiazione) ed un lavoro del fisico teorico italiano Adolfo Bartoli.

    Il passo di Boltzmann, elaborato nelle due memorie Über eine von Hrn. Bartoli entdecke Beziehung der Wärmestrahlung zum zweiten Hauptsatz (Sulla scoperta del Sig. Bartoli della relazione esistente  tra la radiazione termica ed il secondo principio, Annalen der Physik und Chemie 22; 31-39; 1884) e Ableitung des Stefan’schen Gesetzes betreffend die  Abhängigkeit der Wärmestrahlung von der Temperatur aus der  electromagnetischen Lichttheorie (Deduzione della legge di Stefan riguardante la dipendenza della radiazione termica dalla temperatura a partire dalla teoria elettromagnetica della luce, Annalen der Physik und Chemie 22; 291-294; 1884), era estremamente ardito: la radiazione veniva assimilata ad un gas! Ed allo stesso modo di un gas veniva trattata. Già Maxwell aveva stabilito che una radiazione doveva esercitare una data pressione p incidendo su una data superficie; il valore ricavato da Maxwell per questa pressione era:

(3)                                               

dove E è proprio la densità o energia per unità di volume della radiazione vista nella formula di Stefan. L’ipotesi di Maxwell risultava in accordo con un fondamentale teorema stabilito dallo stesso Boltzmann, il teorema di equipartizione dell’energia, relativo però ai gas. Boltzmann prese quindi per buona la relazione di Maxwell, assimilò la radiazione ad un gas, estese l’equipartizione dell’energia alla radiazione e, infine, applicò il secondo principio della termodinamica al gas di radiazione. Seguiamo, per sommi capi, i conti di Boltzmann.
    Supponiamo che una radiazione sia confinata in un cilindro ‘nero’ dotato di stantuffo mobile perfettamente riflettente. La pressione di radiazione sulla base dello stantuffo lo fa sollevare, compiendo un lavoro (il volume del cilindro passa da V a V + dV). Affinché la temperatura resti constante sarà necessario fornire una quantità di calore dQ e, per il primo principio della termodinamica, risulta (si ricordi che U è l’energia interna e che vale la relazione U = E·V):

dQ = dU + p·dV = d(E·V) + ⅓E·dV = VdE + EdV + ⅓ E·dV = V·dE + 4/3.E·dV.

Ma poiché il sistema si è espanso di dV, anche la sua entropia S avrà subito una variazione dS = dQ/T , e cioè:

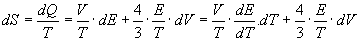
E, dato che l’entropia è una funzione di stato (1/T è fattore integrante del calore), essa sarà rappresentata da un differenziale esatto e varrà quindi la seguente identità:

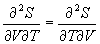
e cioè:

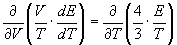
da cui, risolvendo successivamente e tenendo conto (al primo membro) che E, per un dato volume, è funzione della sola temperatura e (al secondo membro) che sia E che T vanno derivate rispetto a T, si trova successivamente:

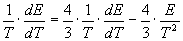
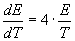
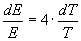
log E = 4.logT + log c

log E = log (cT)⁴

E = c⁴.T⁴

E = k₁.T⁴

E quest’ultima, come si vede, è identica all’espressione data empiricamente da Stefan. Il fatto è estremamente importante perché, oltre a mostrare la correttezza della formula empirica di Stefan, verifica la bontà di una ipotesi (gas di radiazione) che diventerà abbondantemente utilizzata fornendo fecondissimi risultati.

BIOGRAFIA SCIENTIFICA DI WILHELM WIEN

    Fu il tedesco Wilhelm Wien che, nel 1893, fece il passo successivo nella determinazione di f (ν,T) che, per quanto visto nella relazione (3) e nella nota (3), è ricondotta alla ricerca della E (ν,T).

    Wien era nato nel 1864 a Fischhausen, un centro della Prussia orientale, oggi facente parte della Russia. La sua famiglia di proprietari terrieri, a seguito di problemi economici, si era trasferita nel 1866 a Rastenburg dove Wilhelm portò avanti i suoi studi fino al 1879 quando si trasferì alle scuole di Heidelberg che frequentò dal 1880 al 1882. Nel 1882 passò all’Università prima di Göttingen quindi di Berlino dove lavorò nei laboratori di Helmholtz (1883-1885) e conseguì il dottorato nel 1886 con una tesi sulla diffrazione della luce sui metalli e sull’influenza dei materiali sui colori della luce rifratta.

    Da questo momento e fino al 1890 i suoi studi non poterono proseguire come avrebbe voluto perché, a seguito di una malattia di suo padre, dovette badare agli affari di famiglia. Nel 1887 riuscì a passare  un semestre con Helmholtz nell’appena realizzato (1885) Physikalisch-Technische Reichsanstalt (Istituto di Fisica Tecnica di Charlottenburg (un quartiere orientale di Berlino), per le ricerche nelle scienze esatte e nella tecnologia di precisione al fine di risolvere problemi industriali) dove fece esperienze sulla permeabilità dei metalli alla luce e alla radiazione termica. Venduta la proprietà di suo padre tornò ai laboratori di Helmholtz, dove questi si era ormai ritirato, ed ottenne di diventarne il Presidente. Mantenne l’incarico fino al 1896 quando passò ad insegnare fisica all’Università di Aquisgrana (o Aix-la-Chapelle) come successore di Philipp Lenard (1862-1947) dove restò fino al 1899, quando passò per un anno ad insegnare fisica all’Università di Gessen prima di essere assunto (1900) per lo stesso insegnamento all’Università di Würzburg, al posto di Röntgen (1845-1923) che, appena 5 anni prima, nel 1895, aveva scoperto casualmente quelli che oggi sono chiamati raggi X (scoperta per la quale fu insignito del Premio Nobel nel 1901, primo Nobel assegnato). 

    In questi anni Wien lavorò intensamente interessandosi, appunto, del problema del corpo nero e della determinazione di quella funzione E (ν,T). Nel 1893 egli pubblicò una sua importante memoria, Eine neue Beziehung der Strahlung schwarzer Körper zum zweiten Hauptsatz der Wärmetheorie (Una nuova relazione tra la radiazione del corpo nero ed il secondo principio della termodinamica, Berl. Ber. pp. 55-62, 1893), nella quale utilizzò il metodo del cilindro chiuso con stantuffo, con il quale Boltzmann  aveva ricavato la relazione di Stefan, per derivare, a sua volta, una proprietà fondamentale della funzione di distribuzione.

LEGGE GENERALE DI WIEN

    Supponiamo di disporre di un cilindro vuoto a pareti perfettamente speculari il cui volume V possa essere variato mediante lo spostamento di un pistone di superficie S. In un tal recipiente non si può avere né emissione né assorbimento di radiazione e pertanto se in esso vi è della radiazione la sua densità E (ν ,T) resterà invariata nel tempo. Sistemiamo all’interno di un tal recipiente un granellino perfettamente nero, piccolo a piacere e di capacità termica piccolissima (quest’ultima ipotesi serve per rendere trascurabile la perdita di energia totale della radiazione a seguito dell’introduzione del granello stesso) In queste condizioni vi sarà uno scambio di energia tra la radiazione totale V·E(ν,T) contenuta nel recipiente ed il granello nero finché nel recipiente non si raggiungerà una densità di radiazione E (ν ,T) di equilibrio che corrisponde alla nuova temperatura T (che dipenderà dalle energie iniziali della radiazione e del granello). Supponiamo ora di togliere il granello e di far variare il volume V del cilindro comprimendo adiabaticamente il pistone con velocità v constante⁽⁶⁾ e piccola (Fig. 1).

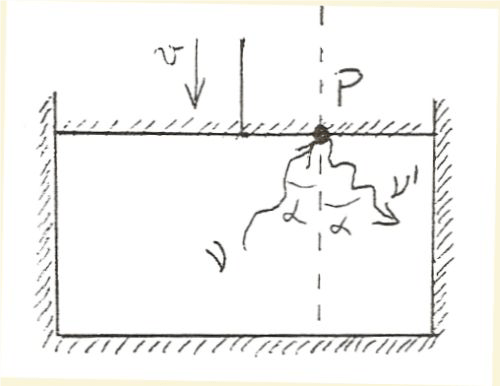
Figura 1

Un’onda di radiazione di frequenza ν si rifletterà, in accordo con l’effetto Doppler, con una frequenza ν’ (più grande di ν) data da:

(4)          

[si può anche dire che la variazione di frequenza per unità di frequenza ν è proporzionale alla velocità di spostamento del pistone secondo la relazione:
 

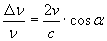
con c velocità della luce. Insomma il punto P di figura si comporta come una sorgente in moto con velocità v]. Passando da una data frequenza ad una maggiore, anche la E (ν,T) varierà  e  con  essa  l’energia  totale della  radiazione W (ν,T), poiché, ricordiamolo, risulta W (ν,T) = V·E (ν,T). Il tutto si potrà pensare come una densità di radiazione che non è variata (è sempre una radiazione nera), a patto di considerarla alla nuova temperatura T. È a questo punto interessante osservare che abbiamo trovato un modo di mettere in relazione T e V. È questa relazione che ci interessa trovare perché, essendo il cilindro adiabatico, mentre è molto difficile misurare T, può risultare più semplice misurare V. Poiché la nostra trasformazione è adiabatica, per il 1º principio (dQ = 0) si ha dU + dL = 0 ed osservando che U è l’energia interna totale della radiazione che abbiamo visto valere V·E (ν,T), si trova:

d[V·E (ν,T)] + p·dV = 0.

Ricordando ora la (1) di Stefan e Boltzmann e l’espressione della pressione di radiazione di Maxwell, nella quale ad E sostituiamo la (1):

=>                      

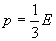
ed inserendo tali relazioni nel 1º principio ora scritto, si trova:

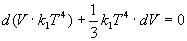
da cui:

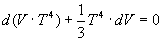
differenziando e successivamente risolvendo la semplice equazione differenziale, si ottiene:

(5)                                   V·T³ = cost.

E questa è la dipendenza di T da V che cercavamo. Si deve però considerare che il conto ora fatto era riferito alla radiazione totale contenuta nel cilindro. Il problema deve essere esteso alla determinazione della densità E (ν ,T) per una variazione dV di volume in corrispondenza della quale si ha una variazione della frequenza a seguito, come già detto, dell’effetto Doppler. In un tempo dt in cui il volume passa da V a V + dV, le frequenze comprese tra ν e ν + dν passano a nuovi valori compresi tra ν ‘ e ν ‘+ dν (e questo cambio di frequenza dovrà sempre essere tenuto presente anche per cambiamenti lentissimi di volume).
Riprendiamo allora in considerazione il nostro cilindro con il granello nero G al suo
interno. La superficie S del pistone in moto è, come già detto, speculare. Come mostrato in Fig. 2, la radiazione è emessa dal granello sotto un angolo solido dΩ (con Ω che rappresenta una semisfera -quella affacciata al pistone che si abbassa -e quindi con 0 ≤ Ω ≤ 2π)⁽⁷⁾. Abbiamo già detto che nell’incidenza della radiazione

Figura 2
 

su S vi è una variazione dell’energia totale  W(ν,T). Per calcolarci questa variazione ΔW osserviamo dapprima che l’energia incidente W su S in un tempo dt sarà data da W=I.S.dt, mentre l’energia della radiazione riflessa  sarà W’=I’.S.dt. Abbiamo quindi:

(6)                                  W – W’ = (I – I’).S.dt = L

avedno posto uguale ad L tale variazione perché rappresenta il lavoro fatto dalla pressione di radiazione:

(6′)                                    L = F.dS = P.S.vdt

La pressione P della radiazione, nel nostro caso, è data da⁽⁸⁾:

(7)                                             

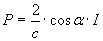
con il fattore 2 che nasce dalla variazione della quantità di moto della radiazione in un urto su S, con α angolo di incidenza della radiazione ed I intensità della radiazione di una data frequenza ν che cade su S in un tempo dt:

    La (6), tenendo conto della (6′), diventa successivamente:

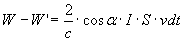
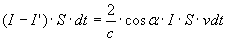
(8)                                           

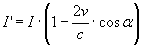
    Passiamo ora alla variazione dell’energia della radiazione che si ha nell’urto su S (che si muove con velocità v) in un ambito di frequenza che va da ν a ν + dν in un tempo dt, cioè:

                                              W(ν,T).dν = V.E(ν,T).dν

    C’è ora da osservare che, a seguito dell’effetto Doppler, la radiazione che abbiamo considerato, dopo aver inciso su S, sarà uscita da quell’intervallo di frequenze (ve ne sarà invece una parte che, sempre per effetto Doppler, partendo da un intervallo di frequenze comprese tra ν’ e v’ + dν’, entrerà tra ν e ν + dν a causa della riflessione).

    L’energia ΔV incidente tra ν e ν + dν in un angolo solido dΩ , sullo specchio di area S in un tempo dt sarà invece:

(9)                           ΔW = S.ΔI.dt = S.Δ(K.cosα.dΩ.dν).dt⁽⁹⁾

essendo K la densità specifica della radiazione legata alla densità di energia dalla relazione⁽¹⁰⁾:

(10)                                       

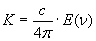
Si ha così:

(11)                             

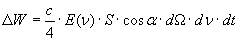
Ricordando il valore di dΩ che ho fornito nella nota (7) si ha successivamente:

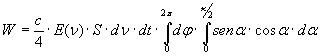
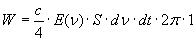
(12)                                         

    Ritorniamo ora un poco indietro per ricordare che, nel passaggio dalla frequenza ν (prima della riflessione) alla frequenza ν’ (dopo la riflessione), anche l’energia  incidente  avrà subito una variazione che l’avrà fatta passare da E(ν) ad E(ν’).⁽¹¹⁾

     Si ha così che la frazione W’ di energia della radiazione che, nelle frequenze
comprese tra ν’ e ν’ + dν’, acquista, nella riflessione, frequenze comprese tra ν e
v + dν è data da:

                                              ∆W’ = S· ΔI’·dt
e, ricordando la (8):

         

e, ricordando la (4), da cui, osservando che ν, α e c sono costanti, si ricava:

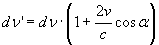
valore che, sostituito nella relazione precedente, fornisce:

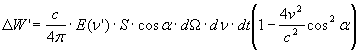
Poiché v << c , i termini v²/c² sono del tutto trascurabili e la relazione diventa:

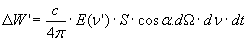
(13)                              

Resta da vedere quanto vale E(ν’). Come già detto si avrà un cambiamento di densità di energia al variare della frequenza che sarà dato da:

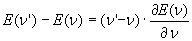
e questa relazione, sviluppata successivamente, tenendo conto della (4) e sostituita nella (13), fornisce:

(14)              

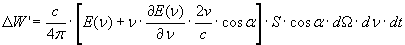
Confrontando la (14) con la (6) scopriamo che il fascio di radiazione incidente sullo specchio S ha acquistato una energia pari alla differenza tra la (14) e la (6), cioè:

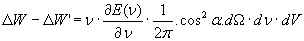
avendo osservato che v.S.dt = dV (variazione di volume del cilindro a seguito dello spostamento del pistone).

    Per calcolare l’aumento totale di energia dovuto alla riflessione, d[E(ν).V], dovremo integrare sull’angolo solido elementare dΩ che diventa una semisfera (ci interessa solo la radiazione diretta verso lo specchio) e cioè per 0 ≤ Ω ≤ 2π:

(15)                     

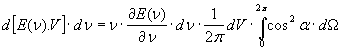
Ricordando il valore di dΩ, dato nella nota (7), l’ultimo integrale vale:

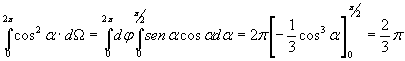
e la (15), rendendo anche esplicito il fatto che la E è anche funzione del volume V del cilindro [si veda la nota (11)], diventa:

(16)                                 

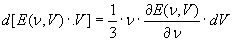
Differenziando i due membri rispetto a V, si ottiene:

(17)                                

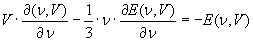
Si tratta di risolvere questa equazione differenziale in E(ν,V)⁽¹²⁾. Intanto è facile vedere che si può porre V = x [vedi nota (12)]. Per capire che valore dare ad y osserviamo che la frequenza ed il volume, come già detto, devono avere un qualche legame funzionale tra loro. Per capirlo basta considerare due soli degli integrali sussidiari di Lagrange:

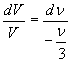
da cui:   

V.ν³ = cost.

ed ecco trovato il legame tra ν e V. E’ spontaneo allora porre:

                                         x = V     ed    y = ν³.V

e le due derivate parziali della (17) diventano:

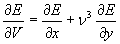
                              e       

e, sostituendo questi valori nella (17), si trova:

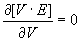
e ciò vuol dire che V·E è una constante rispetto a V risultando funzione della sola ν³.V.
Ritornando allora alla (16) si ha:
 

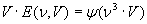
con ψ funzione arbitraria; e quindi:

da cui:

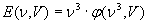
(18)                                   

con φ funzione arbitraria. Ricordando ora la (5), la (18) si può scrivere⁽¹³⁾:

 (19)                                   

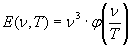
Passando dalla densità di energia E(ν,T) alla distribuzione spettrale della radiazione
(cioè al  potere  emissivo della radiazione con frequenza compresa tra ν e ν + dν) f(ν,T)dν ed inglobando eventuali costanti nella φ, si ha:

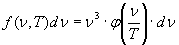
(20)                                 

Se si passa infine dalla frequenza ν alla lunghezza d’onda [ricordando che ν =c/λ => dν = – c·(1/λ²)] si ha:

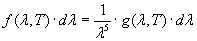
(21)                                 

siamo così giunti alla legge generale di Wien che può essere data o nella forma (20) o nella (21).

Purtroppo la legge di Wien nella sua forma generale non permette un confronto diretto con i dati sperimentali a causa della totale indeterminazione della φ(ν /T) o g (λ·T). C’era però qualcosa che poteva aiutare a comprendere l’eventuale  correttezza dell’elaborazione teorica: che rapporto esisteva tra la legge di Stefan- Boltzmann e quella di Wien ? Riprendiamo la legge di Wien (20) ed integriamola su tutte le frequenze dν:

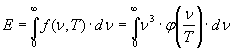
operando per sostituzione (x = ν /T) si trova:

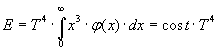
avendo considerato che l’integrale rispetto ad x è una constante rispetto a T. Si ritrova quindi, immediatamente, la legge di Stefan – Boltzmann.

 

LA LEGGE DELLO SPOSTAMENTO DI WIEN

     Il successo del confronto operato lasciava, comunque, in sospeso il problema del confronto con i dati sperimentali. Questi ultimi fornivano delle curve del tipo mostrato in Fig. 3. Ogni curva è relativa ad una determinata temperatura. La T₃ è la più elevata e, decrescendo, vengono di seguito le T₂ e T₁, … Il fatto notevole è

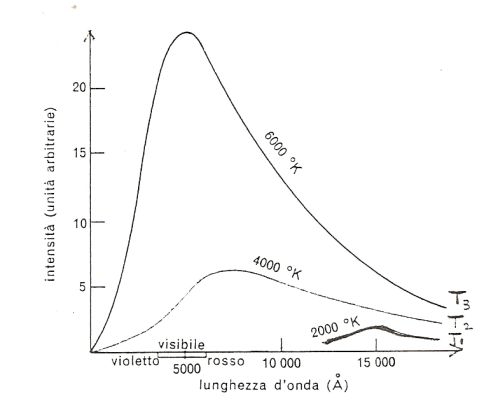
Figura 3

che, sia per piccole che per grandi lunghezze d’onda, l’intensità della radiazione emessa dal corpo nero (e la funzione f di distribuzione) tende a zero. Ciò è indizio dell’esistenza di un massimo nell’andamento della curva in corrispondenza di un dato valore di λ per un fissato valore della temperatura T. La (21) ci fornisce l’opportunità di cercare un tale massimo e di farne un confronto con i dati sperimentali. Fissata una data T, deve risultare:

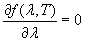
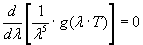
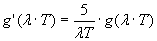
(22)                                         


Questa equazione differenziale fornisce immediatamente(14):

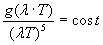
(23)                                           


La (23) è soddisfatta per:
 

(24′)                                       λ T = cost. ⁽¹⁵⁾

E, poiché si lavorava a T = cost, il massimo lo si ha per il valore di  λ che moltiplicato per quella T soddisfa la (24′). Indicando questo valore con  λ_m si ha:

(24)                                     λ_m.T = cost

che è la ben nota legge dello spostamento di Wien (1893) la quale dice che nello spettro normale di emissione da un corpo nero ciascuna lunghezza d’onda si sposta con l’aumento della temperatura in modo tale da mantenere costante il prodotto tra temperatura e lunghezza d’onda.

    La (24) dice proprio ciò che ci veniva fornito dai dati sperimentali: poiché il prodotto λ_m.T è costante, al crescere della temperatura T, il massimo della funzione f(λ,T) si trova in corrispondenza di una lunghezza d’onda λ che diminuisce (e  viceversa). Riguardo infine alla constante che compare nella (24) è evidente che non c’è modo di determinarla finché non si determina la forma della funzione g(λ.T). A questo riguardo lo stesso Wien, nel discorso che tenne quando gli fu conferito il Nobel nel 1911(for his discoveries regarding the laws governing the radiation of heat), sostenne che la termodinamica aveva dato tutto ciò che poteva alla soluzione del problema e che la maniera in cui ad una data temperatura l’intensità della radiazione è distribuita tra le diverse lunghezze d’onda, non può essere determinata dalla termodinamica⁽¹⁶⁾.

    In ogni caso Wien aveva continuato a studiare il problema e nel 1894 aveva pubblicato una nuova memoria, Temperatur und Entropie der Strahlung (Temperatura ed entropia di radiazione, Annalen der Physics, 52: 132-173), nella quale aveva trattato a fondo la termodinamica della radiazione. Due anni dopo pubblicò un terzo lavoro fondamentale sull’argomento.

LA LEGGE DELL’IRRAGGIAMENTO DI WIEN

     Già Wien si andava convincendo dell’impossibilità di andare oltre utilizzando la termodinamica, quando un lavoro⁽¹⁷⁾ di Friedrich Paschen (1865-1947) del 1895/96 gli suggerì una nuova possibilità di investigazione che faceva però ricorso a metodi statistici.
    La nuova idea da cui prese le mosse Wien per la sua memoria del 1896, Über die Energievertheilung im Emissionsspectrum eines Schwarzen Körpers (Sulla distribuzione di energia nello spettro di emissione del corpo nero, Ann. der Phys., 58, pp. 662-669; 1896), era la seguente: un gas fortemente riscaldato può essere considerato come una sorgente di radiazione nera, anche se si ignoravano le cause della radiazione medesima. E poiché, già si sapeva, la temperatura di un gas dipende dalla velocità delle molecole che lo costituiscono, ecco entrare in gioco la formula che nel 1860 aveva ricavato Maxwell per la legge di distribuzione delle velocità molecolari. Questa legge, ricavata con metodi eminentemente statistici, rifacentesi appunto alla statistica di Maxwell-Boltzmann, afferma che in un dato gas ad una fissata temperatura il numero dn di molecole che ha una velocità compresa tra v e v + dv è dato da:
 

(25)                           

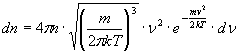
dove: n è il numero totale delle molecole del gas, k è la costante di Boltzmann, T è la temperatura assoluta a cui si trova il gas, m è la massa di una molecola⁽¹⁸⁾.

    Al variare di T la (25) fornisce il grafico di Fig. 4, dove si vede che la curva tende ad ‘appiattirsi’ al crescere della temperatura.

Figura 4

    Queste curve devono aver suscitato in Wien l’esistenza di  una qualche assonanza con le curve sperimentali di f(λ,T) in funzione di λ per un corpo nero. Sta di fatto che il lavoro di Wien iniziò con ipotesi azzardate. Come già detto, egli partì con il considerare, alla stregua di un corpo radiante, un gas racchiuso in un recipiente con pareti riflettenti che potere irradiare verso lo spazio vuoto attraverso un vetro trasparente. La prima ipotesi di Wien è che questo corpo radiante, ad una data temperatura, si comporti come un corpo nero alla stessa temperatura. Wien ipotizza poi che questo gas possa assorbire in modo finito le radiazioni di tutte le lunghezze d’onda e possa irradiare a seguito di sola eccitazione termica. Infine l’ipotesi più forte: la lunghezza d’onda e l’intensità della radiazione emessa da una molecola ad una data temperatura T devono, in qualche modo, poter essere messe in relazione con la velocità della molecola medesima. Questo ‘qualche modo‘ è attraverso la (25)⁽¹⁸⁾. In questo considerare le cose ogni molecola viene trattata come un oscillatore armonico che possiede lunghezza d’onda ed intensità funzioni della sola velocità della molecola, di modo che v = v(λ).
    La funzione di distribuzione f (λ,T) della radiazione emessa con lunghezze d’onda comprese tra λ e λ + dλ deve essere una funzione sia del numero delle molecole che emettono radiazioni di tale lunghezza d’onda, sia della loro velocità. Si dovrà cioè avere:
 

(26)                          

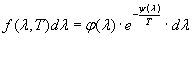
con funzioni φ(λ) e ψ(λ) da determinarsi. Ma Wien aveva già trovato la sua legge  generale (21), dalla quale era poi possibile ricavarsi la legge di Stefan-Boltzmann. A questo punto, l’unico modo per poter ammettere la validità della (21) insieme alla legge dello spostamento è che le due funzioni φ e ψ assumano rispettivamente i valori:

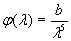
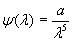
di modo che la (26) diventa:

(27)                                        

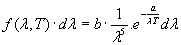
con a e b costanti da determinare.

    È questa la legge dell’irraggiamento di Wien che trovò subito accordo con l’esperienza ma solo nella regione delle piccole lunghezze d’onda (ma quest’ultimo aspetto non era particolarmente significativo in quanto le misure in tale regione erano ancora poco attendibili)⁽¹⁹⁾. Sembrava quindi di disporre di una legge per l’irraggiamento che andasse sostanzialmente bene. L’insoddisfazione riguardava piuttosto la base teorica sulla quale era poggiata la legge stessa. Poco più tardi, all’inizio del 1900, quando si dispose di misure attendibili (eseguite presso l’Istituto di Fisica di Charlottenburg da Paschen, da F. Kurlbaum, da Pringsheim, da Rubens ed altri con il bolometro di Langley opportunamente perfezionato), si scoprì che la formula di Wien era valida solo per le piccole lunghezze d’onda e quindi il problema del corpo nero si riapriva drammaticamente, perché la fisica nota sembrava aver dato tutto. E, come più volte ricordato, sul problema della radiazione del corpo nero molti fisici si erano indirizzati in tutta Europa ed iniziavano a farlo degli Stati Uniti. Tra questi Max Planck che aveva studiato in quell’Istituto di Fisica come allievo di Kirchhoff e dove aveva conseguito la cattedra di Fisica Teorica. Egli dedicò al problema del corpo nero una gran mole di lavori che furono pubblicati in cinque memorie tra il 1897 ed il 1899. Nel suo approccio al corpo nero Planck cambiò più volte il suo punto di vista soprattutto per l’aiuto di Boltzmann che gli faceva notare gli errori presenti nelle prime impostazioni. Il problema arrivò alla sua definitiva soluzione solo in un altra famosissima memoria di Planck del dicembre del 1900, quella in cui Planck introdusse i quanti di energia. Ma ho trattato tutto questo in un lavoro al quale rimando La nascita della teoria dei “quanti”. I lavori di Planck (a partire dal paragrafo 1.7).

 

ALTRI LAVORI DI WIEN

    Avevamo lasciato Wien Professore di Fisica a Würzburg nel 1900, anno in cui pubblicò il suo testo di idrodinamica: Lehrbuch der Hydrodynamik. Le tappe successive della sua carriera accademica che si intrecciano con altri suoi lavori, sono i seguenti. Nel 1902 non accettò la chiamata a succedere a Boltzmann all’Università di Lipsia e nel 1906 quella a succedere a Drude all’Università di Berlino. Accettò invece l’invito fattogli per l’insegnamento a Monaco nel 1920 ed in questa Università restò per il resto della vita.

    Lavorò all’Istituto di Fisica Tecnica sul complesso problema delle misure di alte temperature e, quando nel 1896 andò ad insegnare ad Aquisgrana per succedere a Lenard, egli realizzò in questa Università un laboratorio per lo studio delle scariche elettriche nel vuoto. A seguito di tali studi sperimentali nel 1897 pubblicò un lavoro sulla natura dei raggi catodici nel quale confermò la scoperta fatta da Perrin due anni prima: i raggi catodici sono costituiti da particelle cariche negativamente che sono espulse dal catodo in modo estremamente rapido (è una delle prime evidenze degli elettroni che erano studiati a Cambridge, in Gran Bretagna, da J.J. Thomson che ne determinò il rapporto tra carica e massa).

    Nel 1898 iniziò a studiare i raggi canale scoperti da Goldstein e da tali studi egli arrivò a concludere, dalla deviazione che subivano attraversando un campo magnetico, che si trattava di un qualcosa di analogo ai raggi catodici ma costituito da particelle di carica positiva. Sui raggi canale egli lavorò molto ed ancora nel 1912 e nel 1918 pubblicò dei lavori su di essi. Nel 1919, dopo i fondamentali lavori di Rutherford in Gran Bretagna, quelle particelle di carica positiva furono identificate come protoni. Il metodo usato da Wien diventerà utilissimo nella spettrografia di massa che si svilupperà a partire dal 1912 (il primo strumento del genere fu realizzato da J.J. Thomson). Con gli spettrografi si lavorerà intensamente per la misura delle masse atomiche e dei loro isotopi ed anche per il calcolo delle energie in gioco nelle reazioni nucleari.

    Nel 1898 Wien si sposò con Luise Mehler con la quale ebbe quattro figli.

    Nel 1900 Wien pubblicò una memoria teorica sulla possibilità di dare delle basi elettrodinamiche alla meccanica, Über die Möglichkeit einer elektromagnetischen Begründung der Mechanik (Sulla possibilità di dare fondamenti elettromagnetici alla meccanica, Annalen der Physik, 5, 1900, S. 501–513). A questa memoria ne seguì un’altra nel 1904, Über die Differentialgleichungen der Elektrodynamik für bewegte Körper (Sulle equazioni differenziali dell’elettrodinamica dei corpio in movimento, Annalen der Physik (Series 4), 13(4), 641-662, 663-668) questione che era, anch’essa, al centro del dibattito e delle polemiche in quegli anni e che sfociò nel lavoro di Einstein del 1905 su L’elettrodinamica dei corpi in movimento. Secondo Wien, invece di cercare di ridurre l’elettromagnetismo alla meccanica, come aveva fatto Maxwell, occorreva spiegare la meccanica dei corpi ordinari utilizzando la teoria elettromagnetica. Il progetto era diventato d’interesse da quando nel 1897 J.J. Thomson aveva scoperto l’elettrone, cioè una massa dotata di carica (Cathode-rays, memoria pubblicata sul Philosophical Magazine 44, 293–31). Non sembrava impossibile che la materia fosse costituita solo da particelle cariche. La difficoltà di questo programma risiedeva tutta nella spiegazione della massa ordinaria e Wien suggeriva di utilizzare quanto ricavato da J.J. Thomson, da Heaviside ed altri e cioè di considerare una particella carica in movimento come dotata di una massa maggiore della sua massa in riposo a seguito di effetti di autoinduzione. Nasce in tal modo il concetto di massa elettromagnetica. Una particella carica in moto crea un campo elettromagnetico. L’accelerazione positiva o negativa su tale particella rappresenta un taglio alle sue linee di forza che genera una forza agente sulla particella medesima. Ma il fenomeno di autoinduzione si oppone alla causa che lo genera e quindi al fatto che la particella carica  subisca un’accelerazione. Questo fatto può essere pensato come se la particella avesse una massa maggiore (occorre una forza maggiore per accelerarla), massa che aumenta con la velocità che ha la particella. Avviene anche che la massa della particella in direzione longitudinale differisce dalla massa in direzione trasversale a seguito della configurazione delle linee di forza che non è la stessa nelle due direzioni. Vi è poi da aggiungere un altro fenomeno, l’induzione mutua tra differenti parti dell’elettrone.

    Il primo lavoro di Wien spinse Max Abraham ad avanzare la teoria (1902) secondo la quale tutta la massa è elettromagnetica scontrandosi con una gigantesca difficoltà: cos’è che tiene unita una particella carica, ad esempio un elettrone ? Una particella carica dovrebbe esplodere perché le sue parti avrebbero medesima carica ad una distanza infinitamente piccola. Un altro percorso di indagine che arriverà a compimento con il lavoro di Einstein del 1905 su L’elettrodinamica dei corpi in movimento (volgarmente noto come il lavoro sulla Relatività).

    Insomma si può certamente dire che Wien è proprio al momento di transizione tra l’Ottocento ed il Novecento, un fisico che raccoglie in sé al massimo livello tutte le problematiche che porteranno ai grandi rivolgimenti di fine Ottocento ed inizi Novecento. Ed egli contribuì grandemente a questa transizione anche con la direzione degli Annalen der Physik che dal 1906 condivise con Planck.

Congresso Solvay del 1911 a Bruxelles. Wien è seduto, al centro, dietro Jean Baptiste Perrin e Maria Curie. I presenti sono: (seduti da sinistra) Nernst, Brillouin, Solvay, Lorentz, Warburg, Wien, Perrin, Madame Curie, Poincarè (e, in piedi da sinistra) Goldschmidt, Planck, Rubens, Sommerfeld, Lindemann, De Broglie, Knudsen, Hasenöhrl, Hostelet, Herzen, Rutherford, Kamerlingh Onnes, Einstein, Langevin. [Informazioni sui Congressi Solvay, primi congressi di fisica, si possono trovare in http://en.wikipedia.org/wiki/Solvay_Conference ]

Congresso Solvay del 1913 a Bruxelles. (Da sinistra in piedi ultima fila) Verschaffelt, von Laue, Rubens, Goldschmidt, Herzen,  Lindemann, de Broglie, Pope, Gruneisen, (ancora in piedi, fila intermedia) Hasenohrl, Jeans,  W. L. Bragg, Marie Curie, Sommerfeld, Albert Einstein, Knudsen, Langevin (ultimo a destra, in piedi), (e, seduti da sinistra) Nernst,   Rutherford, Wien, J.J. Thomson, Warburg, Lorentz, Brillouin, Barlow, Kamerlingh Onnes, Wood, Gouy, Weiss.

Wien in prima fila ed al centro in una riunione del 1919 subito dopo la Prima Guerra Mondiale. Wien fu tra i firmatari del “Manifesto dei 93“, firmato appunto da 93 grandi intellettuali tedeschi [http://fr.wikipedia.org/wiki/Manifeste_des_93] e dal titolo Aufruf an die Kulturwelt tradotto poi in francese come Appel des Intellectuels allemands aux Nations civilisées. Tale manifesto fu redatto per rivolgersi a tutte le nazioni europee che, a detta dei firmatari, avevano falsificato la storia nel parlare delle atrocità tedesche nell’invasione del Belgio e nella battaglia della Marna del 1914. Invocando Kant, Goethe e Beethoven, si trattava del sostegno al Kaiser Guglielmo II, all’impero tedesco ed al suo esercito. Altri firmatari noti furono: Nernst, Ostwald, Lenard, Klein, Planck, Roentgen, Wundt. Tristi presagi per il futuro, con alcuni di questi firmatari, tra cui Planck, che si ravvederanno in seguito.

    Si spense a Monaco nel 1928.

NOTE

(1) La natura della f (ν,T) che dipende sia dalla frequenza che dalla natura della radiazione, rende il  problema della sua determinazione sia di natura elettromagnetica (ν) che di natura termodinamica  (T). Questa seconda natura è poi alla base di due possibili trattazioni: quella che discende dalla  termodinamica del macroscopico (Clausius) e quella che discende dalla termodinamica statistica (Maxwell, Boltzmann, Gibbs), ambedue classiche. Vedremo che la termodinamica ordinaria non  permette la soluzione completa del problema fornendo solo risultati parziali in accordo con  l’esperienza. La meccanica statistica fornisce invece soluzioni complete ma in totale disaccordo con l’esperienza.

(2) Tyndall aveva misurato la radiazione emessa da un filo di platino scaldato mediante effetto Joule. Egli, nel suo  On radiation (uno scritto del 1865 contenuto nel suo libro Fragments of Science del 1871) descrive un esperimento in cui un aumento di temperatura di un corpo incandescente aumenta la radiazione invisibile o infrarossa insiema a quella visibile. Egli costruì una tabella in cui era riportata l’energia della radiazione oscura all’aumentare della radiazione della sua sorgente (un filo di platino avvolto a spirale), tabella dalla quale prese i dati Stefan.

(3) Sarà  Boltzmann a mostrare che la E è legata alla W dalla relazione:

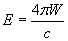
 dove c è la velocità della luce.

 (4) Dopo questo importante lavoro, Stefan si occupò di questioni riguardanti i ghiacci sulla superficie della Terra ed in particolare delle calotte polari (in questo seguendo lavori analoghi di Tyndall). Altri suoi lavori  riguardarono: la tensione superficiale e l’evaporazione (studi dai quali venne introdotto quello che oggi è noto come numero St di Stefan); le correnti alternate ed i coefficienti d”induzione (scrisse le equazioni del campo elettromagnetico in notazione vettoriale); l’ottica (scoprì degli anelli secondari rispetto a quelli scoperti da Newton).

Stefan si spense a Vienna nel 1893.

(5) Il teorema di Equipartizione dell’energia afferma che le molecole all’equilibrio termico hanno la stessa energia media associata a ciascun grado di libertà di movimento. Tale energia è data da ½ kT per molecola ed ½ RT per mole (essendo k la costante di Boltzmann ed R la costante dei gas). Nel caso di un gas monoatomico si devono considerare tre gradi di libertà traslazionali di modo che le energie cinetiche medie date prima diventano rispettivamente 3/2 kT  e 3/2RT . Quando si hanno molecole con strutture più complesse occorrerà aggiungere le energie degli altri gradi di libertà (traslazionali, rotazionali, vibrazionali, …).

(6) Se v non fosse constante sarebbe necessario sostituirla con la derivata dello spazio percorso dal pistone rispetto al tempo.

(7) Questa limitazione per Ω è implicita nella limitazione già data per α che deve essere compreso tra 0 e π/2. Si ricordi che in coordinate cartesiane risulta: dΩ=dS.cos(θ/R²) dove dS è l’elemento di superficie che seziona un cono con vertice nel centro di una sfera, R è il raggio di tale sfera e θ è l’inclinazione di tale elemento di superficie rispetto ad R. Per il concetto di angolo solido e per il cambiamento delle sue coordinate da cartesiane in sferiche si può vedere qualunque testo di Analisi Superiore.

(8) Una pressione di radiazione è l’energia della radiazione divisa per la velocità della luce. L’energia della radiazione è data dalla variazione della quantità di moto nell’urto, per una velocità, divisa un volume; è cioè un’energia divisa per una superficie per un tempo.

(9) L’intensità I della radiazione è data dalla sua intensità specifica K moltiplicata per quei fattori che rendono conto: della direzione di propagazione della radiazione (α), dell’angolo solido elementare (dΩ), della frequenza considerata (dν).

(10) Da ora fino ad avviso diverso, indicherò la E (ν,T) come funzione della sola ν, perché questa è ora l’unica variabile che interessa. Si deve però tenere conto del fatto che T varia nel tempo al variare del volume V e, come vedremo, occorrerà considerare la E (ν,V).

(11) Quest’ultima variazione discende solo dalla variazione della frequenza che deriva a sua volta dalla variazione di volume. La E è quindi funzione di frequenza ν e volume V, con una qualche relazione che deve legare ν e V.

(12) Si tratta di una equazione di Lagrange del tipo:

(I)                                         

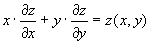
che si risolve mediante le equazioni sussidiarie di Lagrange che, nel nostro caso, sono:
(II)                                            

Da questo sistema, se si riescono a ricavare due integrali indipendenti u e v, allora la funzione arbitraria φ(u,v) = 0 è un integrale della funzione data. Nell’esempio fatto, ricavando dalla (II) i due integrali z = ay e z = ax, l’integrale della (I) è:

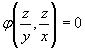
(13) Questa sostituzione è necessaria per rendere la relazione indipendente da V, cioè dal volume e la forma del recipiente in cui è contenuta la radiazione. Si ritorna quindi ad una funzione di ν e T, come annunciato in nota (10).

(14) La (22) si risolve con un semplice cambiamento di variabile x = λT. Si ha poi:

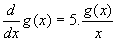
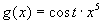
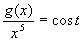
 Si noti a parte che sostituendo la (23) nella (21) si trova f(λ,T) = cost .T^5. Si Può anche definire:

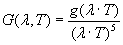
e, sostituendo quest’ultima espressione nella (21), si trova:  f(λ,T) = T⁵.G(λ.T).

(15)  Ponendo nella (23) x = λT e cost = 1, si ha: g(x) – x⁵ = 0; ciò vuol dire che la differenza tra le due funzioni g(x) ed x⁵ per uno stesso valore di x (x = cost) in corrispondenza del quale le due funzioni assumono lo stesso valore (si intersecano). La cosa si vede bene nel caso g(x) sia una funzione algebrica [es. g(x) = x⁶]; si avrebbe: x⁶ – x⁵ = 0    =>    x = 0; x = 1, che sono le ascisse dei punti di intersezione tra le due funzioni. Per funzioni non algebriche si può sempre operare mediante uno sviluppo in serie di Taylor.

(16) La legge dello spostamento di Wien è in accordo con i dati sperimentali come si trovò a posteriori (nel 1895 fu Paschen a dimostrarne la correttezza). Ma, a priori, è impossibile assegnare un valore alla constante che figura nella (24). Ciò vuol dire che non è escluso che tale constante sia nulla, fatto dal quale discenderebbe che un massimo di emissione si dovrebbe avere a qualunque temperatura in corrispondenza di λ_m = 0. Quindi la termodinamica non esclude che la legge di emissione sia rappresentata da una funzione f(ν,T) sempre crescente al crescere della frequenza ν (anche se l’esperienza dice esattamente il contrario). In definitiva i risultati di Wien, pur non essendo in contrasto con l’esperienza, non risolvono il problema del corpo nero in modo univoco: è indeterminata la constante ed è indeterminata la funzione g(λT).

   

                         (a)                                                                   (b)

Il discorso che Wien fece quando ricevette il Nobel si può trovare in http://nobelprize.org/nobel_prizes/physics/laureates/1911/wien-lecture.html

(17) Über Gesetzmässigkeiten in Spectren fester Körper und über eine neue Bestimmung der Sonnentemperatur, pubblicato in Göttinger Nachr., pp. 294-305 (1895) e Über Gesetzmässigkeiten in den Spectren fester Körper, erste Mittheilung, pubblicato in Ann. der Phys., 58, pp. 455-492 (1896).

(18) Per una trattazione della distribuzione maxwelliana delle velocità molecolari si può vedere: il mio articolo in proposito oppure Max Born, Atomic Physics, Ed. Blackie (London), 1935 al Cap. 1, par. 6 e L Landau e E. Lifchitz, Physique Statistique, Ed. MIR (Mosca), 1967 pag. 100 e segg. Per il calcolo di integrali collegati si può vedere ancora Born, all’ Appendice 1.

(19) Le misure sperimentali, all’epoca, erano molto rare anche perché non vi erano strumenti adeguati. Alcune misure erano di H. F. Weber (Untersuchungen über die Strahlung fester Körper, su Berl. Ber., 1888) e ad esse si riferì all’inizio dei suoi lavori Wien. Ma la vera svolta si ebbe intorno al 1880 quando l’astrofisico

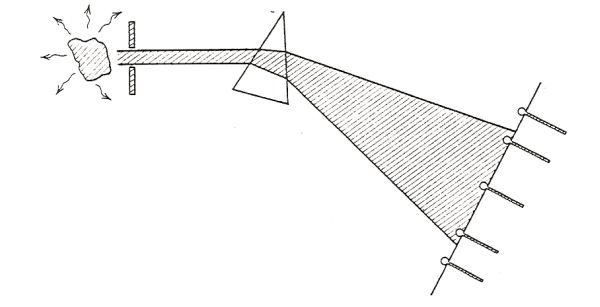
Schema di strumento in uso per la misura delle temperature delle temperature a varie lunghezze d’onda prima dell’introduzione del bolometro.

americano Samuel Pierpont Langley (1834-1906) realizzò il bolometro (misuratore di radiazione) uno strumento che aveva una sensibilità di un ordine di grandezza superiore a quella delle termocoppie sino ad allora usate (il bolometro fu illustrato per la prima volta da Langley nel 1881 nella sua memoria The Bolometer and Radiant Energy, pubblicata su Proceedings of the American Academy of Arts & Science, 1881,  16: 343; 1881. In linea di principio si tratta di un ponte di Wheatstone collegato a due strisce di platino. Quando una striscia è colpita da una radiazione, la sua resistenza elettrica varia leggermente rispetto a quella dell’altra striscia: la differenza indica la quantità di radiazione ricevuta. Lo strumento aveva una grande versatilità nel rilevare l’intensità della radiazione in un vasto range di lunghezze d’onda, dal lontano infrarosso all’ultravioletto). Con tale strumento, lo stesso Langley realizzò molte misure alcune delle quali riportate in Observations on Invisible Heat-Spectra and the Recognition of Hitherto Unmeasured Wavelenghts, Made at the Allegheny Observatory, pubblicato su Phil Mag.21, pp. 394-409, (1886). Se si fa attenzione infatti ai lavori sul corpo nero dal 1860 al 1895 si scopre che essi sono stati essenzialmente teorici. Lo strumento, a partire dal 1892, fu perfezionato nell’Istituto di Fisica Tecnica di Charlottenburg da Otto Lummer e dal suo assistente Ferdinad Kurlbaum (Lummer, Kurlbaum, Bolometrische Untersuchungen, Annalen der Physics, 1892, 46: 204-224 e Lummer, Kurlbaum, Zeitschrift für Instrumentenkunde, 1892, 12: 81-89).

Il laboratorio per lo studio della radiazione del corpo nero all’Istituto di Fisica Tecnica di Charlottenburg.

L’apparecchio realizzato nel 1898 da Lummer e Kurlbaum per lo studio della radiazione del corpo nero il cui modello da loro realizzato è all’interno del cilindro indicato con C. In tale modello di corpo nero la radiazione poteva raggiungere l’equilibrio termico prima che se ne misurasse l’intensità.

Schema del modello di corpo nero situato all’interno del cilindro C della figura precedente.

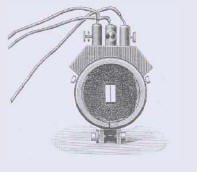
Il bolometro realizzato da Lummer e E. Pringsheim tra il 1897 ed il 1899

    E’ dal 1895, quando si iniziò a disporre di affidabili dati sperimentali, che si realizzò la felice intersezione tra teoria ed esperienza che dette molti frutti eccellenti. Di grande rilievo fu anche lo sviluppo tecnico, particolarmente della Germania ed il grande contributo agli studi del corpo nero che dette il Physikalisch-Technische Reichsanstalt (Istituto di Fisica Tecnica di Charlottenburg)  che, ricordo, fu fondato con il contributo di Siemens ed il fondamentale apporto teorico di Helmholtz. Fu qui che nel 1895 Lummer e Wien misero a punto la prima sorgente di radiazione di corpo nero basata sull’idea di una cavità isoterma ed ancora qui che, alla fine del secolo, si conseguirono i dati sperimentali che più furono utili, particolarmente per l’uso che ne fece Planck che, a partire dal 1889, fu professore a Berlino.

BIBLIOGRAFIA

(1) AA. VV. – Scienziati e Tecnologi dalle origini al 1875 – EST Mondadori 1975

(2) Emilio Segrè – Personaggi e scoperte nella fisica classica – EST Mondadori 1983

(3) E. Whittaker – A History of Theories of Aether and Electicity – Nelson and Sons 1952

(4) Articoli di Enrico Bellone in: Paolo Rossi (diretta da) – Storia della scienza – UTET 1988

(5) Max Born – Atomic Physics – Blackie & Son, London 1962

(6) Friedrich Hund – Storia della teoria dei quanti – Boringhieri 1980

(7) Guido Tagliaferri – Storia della fisica quantistica – Franco Angeli 1985

(8) Mario Gliozzi – Storia della fisica – in: N. Abbagnano (diretta da) – Storia delle Scienze, UTET 1965

(9) René Taton (diretta da) – Storia generale delle scienze – Casini 1965

(10) John L. Heilbron – I dilemmi di Max Planck – Bollati Boringhieri 1988

(11) Piero Caldirola – Lezioni di fisica teorica – Viscontea, Milano, dopo 1950

(12) Samuel Tolansky – Introduzione alla fisica atomica – Boringhieri 1966

(13) Ludwig Boltzmann – Lectures on Gas Theory – Dover 1995

(14) Max Planck – The Theory of Heat Radiation – Dover 1991

(15) Thomas S. Kuhn – Black-Body Theory and the Quantum Discontinuity 1894-1912 – Oxford University Press 1978

(16) http://www.didaktik.physik.uniessen.de/~backhaus/Quanten/Literatur/

100aQuantentheorie/Hoffmann.pdf

(17) http://nobelprize.org/nobel_prizes/physics/laureates/1911/wien-bio.html

(18) William Berkson – Fields of Force: The development of a World View from Faraday to Einstein – Routledge e Kegan 1981

Categorie:Senza categoria