1 – TRAITÉ DU MONDE O TRAITÉ DE LA LUMIÈRE

1.1 – Come nasce l’opera

        Tra il 1630 ed il 1633, come abbiamo visto, Descartes scrisse il Traité du Monde o Traité de Lumière (che ha come ultimo capitolo il Traité de l’Homme). Ma proprio nel 1633 si ebbe la brutale condanna di Galileo dal Tribunale della Chiesa. Questa notizia convinse Descartes a non pubblicare il suo Mondo⁽¹⁾, che poi è l’insieme delle sue teorie fisiche ed astronomiche basate sul copernicanesimo (il Mondo sarà pubblicato postumo nel 1664). Vediamo quali sono le idee contenute in tale trattato tenendo sempre conto che erano le idee di Descartes del 1633 e che su di esse era ritornato dopo il 1637 in quanto vi figura una citazione della Dioptrique che è del 1637.

         Il Mondo era nella mente di Descartes almeno dal 1629 come ci testimonia una lettera del 13 novembre a Mersenne in cui Descartes dice che ha in mente di stampare un piccolo trattato in cui spiegare tutti i fenomeni della Natura, ossia tutta la Fisica. Questo lavoro egli lo intraprese ma senza affanno come egli stesso confidò a Mersenne in altra lettera del 15 aprile 1630: io lavoro molto lentamente, perché godo molto di più a istruire me stesso che a mettere per iscritto il poco che so). Nella stessa lettera dice che la sua speranza è di consegnargli la sua Fisica, distinta dalla Metafisica,agli inizi del 1633. Tra l’altro egli lavorava simultaneamente anche al Discorso sul Metodo, con le esemplificazioni della Dioptrique, delle Météores, de la Géométrie ed aveva anche in mente quel Trattato di Metafisica (che doveva trattare dell’esistenza di Dio e delle nostre anime separate dal corpo e perciò immortali) che disse aver sospeso quando venne a conoscenza dei pareli che lo fecero impegnare proprio nelle Météores. E’ possibile seguire i progressi di Descartes attraverso la corrispondenza con Mersenne dalla quale risulta anche un’ulteriore precisazione alla volontà di non pubblicare il lavoro. Nell’aprile 1634 scrive a Mersenne:

Tutte le cose che spiegavo nel mio trattato, e fra queste c’era la tesi del movimento della Terra, dipendevano a tal punto le une dalle altre, che basta sapere che una è falsa, per conoscere che tutte le ragioni di cui mi servivo non hanno validità alcuna: e benché io pensassi che poggiavano su dimostrazioni molto certe ed evidenti, per niente al mondo io vorrei sostenerle contro l’autorità della Chiesa. Io so bene che si potrebbe obbiettare a quanto gl’Inquisitori romani hanno deciso, non per questo è senz’altro articolo di fede, e che bisogna innanzitutto che vi sia una deliberazione conciliare. Ma io non sono invaghito a tal punto dei miei pensieri da volermi servire di tali eccezioni per aver modo di mantenerli: il desiderio che io ho di vivere in pace e di continuare la vita che ho cominciato prendendo per motto bene vixit, bene qui latuit, fa sì che io sono più contento di essermi liberato del timore, che avevo, di acquisire, per mezzo del mio scritto, conoscenze superiori ai miei desideri, di quanto io non sia irritato per il tempo perso e la fatica sostenuta per comporlo.

        Ed in questo scritto dimentica ciò che aveva scritto in una lettera allo stesso Mersenne del 14 ottobre 1630:

Attendo alla descrizione della nascita del Mondo, e in essa spero di includere la maggior parte della Fisica. E vi dirò che quattro o cinque giorni or sono, rileggendo il primo capitolo della Genesi, ho trovato come per miracolo che tutto poteva spiegarsi secondo le mie fantasie molto meglio, mi sembra, che in tutti quei modi in cui gl’interpreti lo spiegano – cosa che prima non avevo mai sperato. Mi propongo ora, dopo avere spiegato la mia nuova filosofia, di far vedere chiaramente che essa si accorda molto meglio di quella di Aristotele con tutte le verità della fede.

Quindi Descartes avrebbe potuto sostenere le sue tesi con qualche ragione ma, come egli stesso disse poi nel 1634, bene vixit, bene qui latuit. In ogni caso, come già accennato nella prima parte, il Mondo venne diluito, nelle parti che non implicavano il copernicanesimo, in varie opere: nei Principia Philosophiae, nella Dioptrique, nelle Météores, nel Traité des passions de l’âme. E’ però conveniente prendere in considerazione l’opera nella sua interezza così come era stata pensata e rivista, certamente dopo il 1637, dallo stesso Descartes. Ed il motivo è ben descritto da uno dei più grandi studiosi del filosofo francese, Eugenio Garin:

Forse nessuna delle opere cartesiane rispecchia con l’efficacia del Mondo una ricerca appassionata che intende sostituire all’universo degli Scolastici, e di Aristotele, tutt’altro universo. Nella «favola» del Mondo, ossia nell’ipotesi di un nuovo sistema generale dell’universo fisico, ivi compreso l’uomo, si traduce veramente una nuova «visione» globale della realtà: e proprio come «visione », ossia come intuizione generale non nata dall’esperienza, ma dell’esperienza anticipatrice, e che nell’esperienza cercherà una conferma.

L’incontro olandese del 1618 con Isaac Beeckman, geniale quanto singolare scienziato, aveva avviato Descartes verso una fisica meccanicistica, al di fuori della tradizione scolastica. Il Mondo è il frutto maturo di questo orientamento, ma è anche il documento di una svolta decisiva: da un’indagine che ha al centro matematica e metafisica, Descartes passa a una ricerca fisica, e a una visione fisica del tutto. Per questo, sia nella discussione critica di alcune nozioni essenziali delle teorie aristotelico-scolastiche, che nella delineazione di un «sistema del mondo» comprensivo dell’uomo, il Mondo rappresenta un punto chiave nello svolgimento del pensiero cartesiano. Di più, in certe sue parti, è «un testo che nessuna delle altre opere di Descartes sostituirà», neppure i Principi, che pure vollero essere, e furono, la summa di tutta una ricerca.

D’altra parte, se Descartes dichiara esplicitamente di avere interrotto un discorso metafisico già avanzato («io credo di avere trovato – scrive nel ’30 – come dimostrare le verità metafisiche in modo più evidente delle dimostrazioni geometriche»), con altrettanta chiarezza ribadisce che «non avrebbe saputo trovare i fondamenti della fisica, se non li avesse cercati per quella via », ossia attraverso una metafisica. Se decisa è la svolta fisica, altrettanto precisa è la connessione fra teoria dei fondamenti della fisica e metafisica. Il nesso strettissimo si mostra in tutta la sua evidenza a proposito delle verità eterne e delle leggi di natura. Non a caso il famoso scambio di lettere con Mersenne sulle «vérités éternelles» è del ’30 e coincide con l’impostazione generale del Mondo.

        Impostazione che è un inno continuo a Dio, ad un Dio a sua immagine. Tutto è dovuto a Dio e Dio, grande geometra, ha fatto il mondo come Descartes lo descrive. E Dio interviene dappertutto anche se il sistema sembra essere meccanico. Lo è ma non ha il libero arbitrio perché è Dio che una volta per tutte ha deciso così. E Dio, dal momento della creazione, sembra essere sempre impegnato a regolare le cose nel mondo. Ma che Dio è, se è geometra e la geometria risulta perfettamente comprensibile mentre Lui no ? Il fatto è che Dio serve a Descartes come un gigantesco postulato da cui ricavare, deduttivamente ed a priori, l’universo intero. L’antinomia di una matematica comprensibile e di un Dio che non può esserlo, si ricompone in un mondo che ci è stato reso comprensibile attraverso una geometria che ha le sue basi nella metafisica. Il matematico ed astrologo J. B. Morin (1583-1656) glielo osservò nel 1638 e noi possiamo dirglielo adesso: sembra proprio che Descartes tenti di dimostrare le cause attraverso gli effetti e gli effetti attraverso le cause. In ogni caso si tratta di una ripetizione aggiornata di tutta la filosofia scolastica con un Dio, appunto impegnato a creare e conservare. Ma è meglio passare ora ad un’analisi dei passi più interessanti della Fisica di Descartes, in riferimento a ciò che è di maggiore interesse: la sua concezione del mondo.

1.2 – Il contenuto dei primi sei capitoli

         Il fine più volte esplicitato da Descartes è quello di costruire un’immagine del mondo che fosse fondamentalmente completa e che avrebbe solo richiesto, eventualmente, qualche precisazione in dettagli. E’ vero che si lavora per smontare l’universo aristotelico ma lo spirito è scolastico perché non si procede induttivamente, come Galileo, capendo dei pezzi sparsi in una ipotesi complessiva, la copernicana, e poi, via via, invitando altri studiosi a completare ad analizzare, ad aprire nuovi campi di ricerca. Qui vi è un’ipotesi di mondo (che sarà riportata anche nei Principia, con qualche ampliamento tanto che qualcuno ha definito tale opera un “trattato di fisica teorica ante litteram” confondendo la fisica teorica con eccessi di fantasia) dentro cui inserire i fenomeni noti e le spiegazioni derivate dal suo Metodo che faceva affidamento solo su concezioni matematiche e meccaniche. Come Aristotele, Descartes cercò di mettere all’inizio del suo sistema degli assiomi che riteneva non dubitabili di modo che, necessariamente, andò a postulare una metafisica basata sulla certezza della propria esistenza, di quella di Dio e di alcune idee vere (come visto quando abbiamo parlato del suo Metodo). Tali criteri vennero soddisfatti nella fisica attraverso la sua definizione di materia e di impossibilità di vuoto (come discuteremo ora).

         Dopo una breve discussione sui nostri sensi che ci mettono in contatto con il mondo circostante, per dire che non dobbiamo dare per scontato che l’oggetto che vediamo, udiamo e tocchiamo sia simile alle sensazioni che ce lo fanno conoscere⁽²⁾(capitolo I), Descartes si intrattiene sulla natura del calore, del fuoco, sulla luce che da esso emana (capitolo II) e su come intenderlo se solido – e fin dove – o se fluido (capitolo III). Risulta una cosa straordinaria che cioè i corpi solidi sono quelli le cui parti sono in riposo ed i fluidi sono quelli le cui parti sono in agitazione. Newton, nell’Optiks, osserverà che i corpi sono cementati dal riposo, cioè da una qualità occulta. Ma, a parte queste considerazioni che non sono da poco, Descartes non dice una sola parola quantitativa per spiegare ad esempio cosa vuol dire “più grande” e perché i corpi più grandi  hanno un potere di penetrazione più grande dei più pesanti. Sembra proprio che Descartes non abbia alcun interesse alla meccanica quantitativa perché ciò che a lui interessava era un cambiamento e basta, senza porsi troppi problemi. Nel capitolo IV l’argomento trattato è il vuoto attraverso semplici esemplificazioni che tendono a mostrarne innanzitutto l’impossibilità metafisica e quindi l’impossibilità sperimentale. Inoltre da tali impossibilità deriva anche il tipo di moti che in qualche modo dal vuoto derivano. Intanto egli afferma che se, in natura, si crea un qualche vuoto o interstizio tra particelle, esso tende ad essere riempito. Per spiegarlo inizia a considerare le varie sostanze solide o fluide e dice che se un qualche spazio vuoto può esservi esso è pensabile più nei solidi che nei fluidi. E qui interviene un’osservazione empirica: quando riempiamo un vaso di polvere, possiamo metterne di più se scuotiamo più volte il vaso ma se vi mettiamo dell’acqua non ci sono scuotimenti che permettano di immetterne di più. Inoltre se vediamo una brocca su di un tavolo diciamo che essa è vuota se non vi è dell’acqua. E ciò avviene perché non consideriamo le cose che comunemente ci circondano ma esse ci sono e riempiono tutto, anche la brocca che noi possiamo riempire perché può uscirne l’aria contenuta da dove immettiamo il liquido. Questo argomento è ritenuto risolvente per Descartes, tanto che lo amplierà nei Principia dove argomenta che se Dio togliesse tutto ciò che c’è in un bicchiere le pareti di questo verrebbero a contatto  perché non si avrebbe nulla tra esse. Ed il nulla non può avere proprietà e quindi non può avere dimensioni. In definitiva gli oggetti separati dal nulla sono in contatto. A ciò Mersenne osservò che Dio avrebbe potuto togliere tutta l’aria da una stanza senza rimpiazzarla. E Descartes arrabbiato rispose che certo Dio avrebbe potuto creare valli senza monti … (Descartes a Mersenne, 9 gennaio 1639). Tornando al Mondo, Descartes  passa ad altro esempio più impegnativo per la teoria che comporta. Quando apriamo il rubinetto di una botte per far uscire del vino ed esso non esce noi diciamo che non lo fa perché altrimenti si creerebbe del vuoto nella botte ed in vino ne ha orrore. Queste sono sciocchezze perché il vino non può avere l’horror vacui in quanto le sostanze inanimate non provano sentimenti. Piuttosto le cose vanno così. Il vino non esce perché non saprebbe dove andare trovando fuori il tutto pieno. Ma se apriamo il tappo superiore della botte il vino può uscire perché si genera un moto a catena circolare: il vino dal rubinetto spinge l’aria che ne spinge ancora fino ad andare a riempire da sopra lo spazio che ha lasciato libero il vino che sta uscendo. Ed egli dice che da molte esperienze si è convinto che i moti circolari siano agevoli e familiari alla natura e che, anzi, esistono solo moti circolari, in accordo completo con il Timeo di Platone e tali moti debbono anche essere istantanei. Il vuoto non può esistere perché abbiamo un tutto pieno eternamente in moto. Dice Descartes:

[Ho] appurato con parecchie esperienze che tutti i movimenti che si verificano nel mondo sono in qualche modo circolari: quando, cioè, un corpo lascia il suo posto entra sempre nel posto di un altro, e questo nel posto di un altro ancora e così via fino all’ultimo che occupa nel medesimo istante il posto abbandonato dal primo, dimodoché tra di essi non è più vuoto quando si muovono di quanto ve ne sia quando sono fermi. E va notato a tale proposito che per questo non si richiede che tutte le parti dei corpi che si muovono insieme siano disposte secondo una linea perfettamente circolare e nemmeno che abbiano uguale grandezza e forma, perchè queste disuguaglianze possono essere facilmente compensate da altre disuguaglianze nella loro velocità [Monde; 14; 46]

        Descartes va costruendosi piano piano i pilastri della sua concezione del mondo che esporrà nel capitolo VIII. Egli prosegue ora con altre esperienze che ritiene significative ai suoi fini ed in particolare a far pensare a sostanze sempre più rarefatte fino a quelle che non riusciamo a vedere ma che, come l’aria nella brocca prima, vi sono.

Se ne può trovare una facile conferma nell’esperienza: infatti le parti di una goccia d’acqua, separate l’una dall’altra dall’agitazione del calore, possono formare una quantità d’aria molto maggiore di quanto non ne potrebbe contenere lo spazio dove prima era l’acqua. Ne consegue senza alcun dubbio che fra le parti di cui l’aria si compone ci sono dei piccoli intervalli in gran numero: non c’è altro modo, infatti, di concepire un corpo rarefatto. Ma non potendo, come ho detto prima, questi intervalli essere vuoti, ne concludo che vi sono necessariamente degli altri corpi – uno o più di uno – che, mescolati all’aria, riempiono con la massima esattezza possibile gl’intervalli rimasti tra le parti di questa. Ormai resta solo da esaminare quali possono essere questi altri corpi; dopo, spero non debba essere difficile intendere quale può essere la natura della luce [Monde; 14; 49]

        Si vede subito che da questa esperienza viene tratta una conclusione che è pura speculazione e con l’esperienza medesima non c’entra nulla: mi riferisco al fatto che vi sarebbero non definiti altri corpi pronti a riempire intervalli che dovrebbero rimanere vuoti. Si è arrivati qui con una sorta di processo induttivo. Si capisce quindi che le discussioni precedenti su calore e maggiore o minore fluidità erano una sorta di glossario per iniziare a discutere di ciò che lo interessa che, come nel caso di quanto ora detto sul vuoto, è la natura della luce.

        Il capitolo successivo, il V (nel quale, come accennato, si fa riferimento alla Dioptrique del 1637), è occupato dalla discussione sul numero degli elementi (in senso aristotelico) che devono essere considerati. Descartes riduce i quattro elementi aristotelici a tre: fuoco, aria e terra (assimilando con questa operazione l’acqua all’aria che risultano unite dalla fluidità). Il discorso è comunque articolato perché il fuoco è di due tipi, quello perfetto, puro, che risiede in alto nel cielo e quello ordinario che conosciamo; ed anche l’aria può essere sia quella grossolana che respiriamo ma anche quella che si trova in alto che è più sottile. Il fuoco poi è costituito da entità piccolissime senza forma ma capaci ad adattarsi a qualunque forma sia necessaria per riempire i supposti vuoti che potrebbero crearsi nell’aria a seguito dei continui movimenti; l’aria è comunque costituita da piccoli corpuscoli rotondi, uniti tra loro come granellini di sabbia e dotati di grande velocità, comunque più piccola di quella delle particelle di fuoco per le quali il moto è condizione non solo necessaria ma anche sufficiente. Vi è poi la terra che è costituita da particelle più grandi in lievissimo moto ma anche immobili ed anche la volgare terra che calpestiamo è lontana dall’elemento terra che ha caratteristiche di purezza superiori. C’è da osservare che qui siamo di fronte ad una imprevedibile posizione platonica che serve a Descartes per dire che a lui non interessano le qualità che Aristotele assegna agli elementi (caldo, freddo, umido, secco) perché tutte discendono dalla particolare unione dei tre elementi e dalla loro tendenza a corrompersi:

Soffermatevi quanto volete a esaminare tutte le forme che i vari movimenti, le varie figure e grandezze, la diversa disposizione delle parti della materia possono dare ai corpi composti, e sono certo che non ne troverete nessuna dove manchino qualità tendenti a farla cambiare riducendola nel mutamento a qualcuna delle forme degli elementi.
La fiamma, per esempio, la cui forma, come si è detto prima, richiede parti che si muovano rapidissime e che al tempo stesso posseggano una certa grandezza, non può durare a lungo senza corrompersi: infatti, o la grandezza delle sue parti, rendendole capaci di agire contro gli altri corpi, determinerà una diminuzione del loro movimento; oppure la violenza della loro agitazione, facendole infrangere nell’urto coi corpi che incontrano, determinerà una perdita di grandezza; sicché, un po’ alla volta, potranno ridursi alla forma del terzo elemento, o a quella del secondo, e in qualche caso persino a quella del primo. Di qui potete apprendere la differenza tra questa fiamma, ossia il comune fuoco che troviamo tra noi, e l’elemento del fuoco che ho descritto. E dovete anche sapere che neppure gli elementi dell’aria e della terra, cioè il secondo e il terzo elemento, somigliano all’aria grossolana che respiriamo o alla terra che calpestiamo; ma, in genere, tutti i corpi che si vedono attorno a noi sono misti o composti e soggetti a corrompersi [Monde; 14; 53]

        Dopo questa illustrazione, Descartes ci dice di ritenere che nel mondo esistano dei luoghi dove gli elementi possano conservare in perpetuo la loro naturale purezza. Per convincersene basta osservare il Sole e le stelle fisse, che sono il luogo del fuoco al suo stato puro, quindi i cieli, luogo dell’aria al suo stato puro ed infine la Terra i pianeti e le comete che sono terra allo stato puro. I corpi misti di cui parlava infatti si trovano solo sulla superficie della Terra e nell’aria che respiriamo come una sorta di scorza costituitasi nel tempo. In questa scorza prevalgono gli oggetti che ci appaiono solidi, quelli fatti nella loro maggiore entità di terra ma non bisogna dimenticare che i più reconditi pori di tale materia devono essere riempiti da particelle sottili di aria e da quelle ancora più sottili ed adattabili agli ultimi anfrattini reconditi che sono le particelle di fuoco (anche quando Torricelli dimostrerà l’esistenza del vuoto nel 1644 e Mersenne lo informò della scoperta, questo fatto non turberà la teoria cartesiana: sopra il livello del mercurio, per Cartesio e seguaci, c’è l’etere non il vuoto). E questa zona di mescolamento è comunque poca cosa rispetto all’immensa distesa del Cielo. Ed è a questo punto che Descartes ci informa che descriverà una parte di questo mondo sotto forma di favola ad evitare che ci si possa annoiare.

1.3 – La materia che costituisce il nuovo mondo

        E la favola, raccontata nel capitolo VI, dice che per comprendere ciò che Descartes vuole presentarci occorre immaginare che Dio, cinque o seimila anni fa, abbia creato un mondo indefinito e costituito di una sola materia fantastica che non è assimilabile a nessuno degli elementi prima visti (tale materia è inoltre distinta dallo spirito e la cosa era anche sostenuta da Descartes, come accennato, nella separazione che intendeva tra anima e corpo). A questo punto inizia la spiegazione del come da un’unica materia discendano le proprietà della materia che conosciamo (estensione, peso, impenetrabilità, durezza, …) e del come sia possibile pensare ogni cosa concreta come una parte dell’unica cosa estesa primordiale, come cioè si sia prodotta la differenziazione della materia nei diversi corpi che ci circondano. Con riferimento neppure nascosto alla Genesi, Descartes dice che all’inizio doveva esservi il caos e pian piano le parti del caos sono arrivate a districarsi da sé, disponendosi in  bell’ordine, così da assumere la forma di un mondo perfettissimo, dove si potranno vedere, non solo la luce, ma anche tutte le altre cose, generali e particolari, che compaiono in questo mondo reale. Lo spazio, l’estensione, risulta dunque, per Descartes completamente assimilabile alla materia che lo contiene non distinguendosi in alcun modo da essa e questo è uno degli aspetti fondamentali della sua concezione del mondo che inizierà ad essere sviluppata dal capitolo seguente. Tale spazio, che sembra avere un’estensione infinita è costituito dappertutto dalla stessa materia che risulta infinitamente divisibile. In uno spazio che coincide con la materia con lo contiene il vuoto sarebbe un controsenso, un’assenza di spazio. In questo mondo degli inizi, Dio deve aver diviso lo spazio in parti di diversa forma e dimensione e poi deve aver messo in moto tali parti in tutti i modi possibili. Pian piano (evolutivamente !) si sono formati i tre tipi di particelle (piccolissime ed adattabili, piccole e tonde, rozze ed unite insieme in corpi solidi) che costituiscono i tre elementi.

1.4 – La meccanica di Descartes

        Prima di affrontare la meccanica del mondo che ha abbozzato, ricapitolo in breve le cose di cui dispone Descartes. Un universo presumibilmente infinito e completamente pieno dentro cui da un’unica materia indefinitamente divisibile ed impenetrabile (su queste proprietà Descartes tornerà abbondantemente nei Principia, aggiungendo argomenti) si è passati alle differenziazioni in tre elementi che sono in continuo movimento: Tale movimento deve godere delle proprietà di circolarità ed istantaneità. Inutile dire che questa concezione era veramente favolistica come Leibniz fece osservare. Vediamo: se si dispone di una materia perfettamente solida ed omogenea non si potrebbe avere alcun cambiamento. Affinché il movimento sia potuto nascere e diffondersi attraverso la materia procurandone la divisione, la materia doveva già essere divisa e nello stato fluido. Ma la materia può diventare fluida solo grazie al movimento. Sembrerebbe un discorso circolare ma Descartes ci mette il risolutore di ogni problema: Dio ! Infatti Dio ha creato la materia come un blocco solido (ma non aveva detto Descartes nel capitolo III che la caratteristica di un corpo di essere solido era la sua assenza di movimento ?) e l’ha messa in moto istantaneamente. E, di fronte a tali obiezioni di carattere solo metafisico, la fisica non può nulla.  Eppure la meccanica di Descartes ha solo un fondamento metafisico e lo si dimostra facilmente perché il capitolo VII inizia con un postulato non falsificabile e quindi, con Popper, metafisico fino al punto da dover turbare anche un onesto teologo perché, proprio per ciò che dicevo prima, questo Dio è presente ogni volta che cade un oggetto o si urtano palline, o …

Dio essendo, come tutti devono sapere, immutabile, agisce sempre allo stesso modo [Monde; 14; 62]

         Conseguenza di tale ammissione sono le due o tre leggi del moto che Descartes fissa subito dopo:

 La prima è: che ogni parte della materia in particolare persiste nel medesimo stato finché l’urto delle altre non la costringe a mutarlo. Ossia: se ha una certa grandezza, non diventerà mai più piccola a meno che le altre non la dividano; se è rotonda o quadrata, non muterà mai forma senza che le altre ce la costringano; se è ferma in qualche luogo, non se ne allontanerà mai se le altre non la cacciano; e, se avrà cominciato a muoversi, continuerà sempre con ugual forza, finché le altre non la faranno fermare o rallentare [Monde; 14; 62]

        Questa è la prima regola del moto di Descartes che dovrebbe essere la regola che oggi va sotto il nome di principio d’inerzia. Dopo un paio di pagine in cui Descartes polemizza con presunti filosofi (immaginiamo peripatetici), egli passa alla seconda regola del moto:

Suppongo come seconda regola che, quando un corpo ne spinge un altro, non possa comunicargli alcun movimento senza perderne contemporaneamente altrettanto del proprio; né sottrarglielo senza aumentare il proprio nella stessa misura [Monde; 14; 64-65]

        E questa regola dovrebbe essere la legge che oggi è a noi nota come conservazione della quantità di moto ma con un errore che inficia l’intera proposizione: la velocità introdotta da Descartes ha solo carattere scalare e non vettoriale e ciò, nella supposta conservazione, non fa considerare cambiamenti di direzione e verso del moto come cambiamenti di quantità di moto.

        Queste regole spiegano le osservazioni che facciamo. Infatti quando scagliamo un sasso esso continua a muoversi non perché sarebbe aiutato dall’aria che lo sospinge (come ritengono i peripatetici). Anzi ci si potrebbe chiedere perché questo sasso non continua a muoversi sempre. La spiegazione di ciò sta nel fatto che il sasso rallenta e poi si ferma perché è l’aria a fargli da ostacolo. Se poi si chiede come fa un corpo molle come l’aria a rallentare un sasso la risposta è nella seconda regola che ci dice che il moto del sasso non viene rallentato in proporzione della resistenza dell’aria ma nella misura in cui l’aria cede e, nel cedere, fa sua la forza di muoversi che l’altro perde.

        E Descartes, fattaci altra professione di fede:

anche se la nostra intera esperienza sensibile nel vero mondo apparisse in manifesto contrasto rispetto al contenuto di queste due regole, la ragione che me le ha dettate. mi sembra così salda che continuerei a credere di essere obbligato a supporle nel nuovo mondo che vi descrivo. Infatti, anche nel caso di una scelta del tutto libera, qual fondamento più fermo e più saldo della fermezza e immutabilità che è in Dio potremmo prendere a base di una verità? [Monde; 14; 66]

ricapitola sulle due regole, prima di aggiungere la terza:

Ora le due regole derivano evidentemente solo da questo: che Dio è immutabile e che, con l’agire sempre alla stessa maniera, produce sempre lo stesso effetto. Infatti, supponendo che nell’atto stesso di crearla, Dio abbia posto in tutta la materia in generale una certa quantità di movimenti, a meno di negare che egli agisca sempre allo stesso modo, bisogna ammettere che ne conservi sempre la stessa quantità. Supponendo pure che da quel primo istante le diverse parti della materia in cui i movimenti si sono trovati variamente distribuiti abbiano cominciato a conservarli o a trasmetterli dall’una all’altra, a seconda della loro forza, bisogna necessariamente concludere che Dio le fa continuare sempre allo stesso modo. Le due regole vogliono dire questo [Monde; 14; 66-67]

        Anche qui insiste su un Dio che agisce sempre allo stesso modo, pregiudizio addirittura più forte del dogma di fede, posizione che più volte gli verrà rimproverata da varie persone tra cui Mersenne. In ogni caso Descartes prosegue con la terza regola:

quando un corpo si muove, benché il suo movimento avvenga per lo più secondo una curva e ogni movimento, come si è detto prima, sia sempre in qualche modo circolare, tuttavia, le sue parti, singolarmente prese, tendono sempre a continuare il loro [moto] in linea retta. Quindi la loro azione, ossia la loro inclinazione a muoversi, è diversa dal loro effettivo movimento [Monde; 14; 67]

e, tale regola è confusa. Si potrebbe metterla insieme alla prima e ricavare un principio d’inerzia completo ma non si capisce cosa sono le parti del movimento (non azzardo la composizione dei movimenti) e non si capisce bene l’ultima frase (forse che se non vi fosse il contesto, un pezzo di materia si muoverebbe in linea retta e si muove invece in cerchio perché vi è altra materia ?) se non si ricorre alle esemplificazioni che seguono:

Se, per esempio, si fa girare una ruota intorno al proprio asse, per quanto tutte le sue parti si muovano in cerchio perché, essendo unite fra loro, non potrebbero far diversamente, tuttavia la loro inclinazione è a procedere in linea retta, come si vede chiaramente quando una si distacca dalle altre; infatti, appena libera, smette di muoversi in cerchio e continua in linea retta.

Allo stesso modo, quando si fa rotare un sasso in una fionda, non solo il sasso corre in linea retta appena ne parte, ma, anche stando nella fionda, preme sul centro facendo tendere la corda; e così mostra chiaramente che la sua inclinazione è sempre a muoversi in linea retta e che si muove in cerchio solo perché costretto [Monde; 14; 67-68]

1.5 – Il moto circolare

        Quindi i corpi tendono ad andare in linea retta e solo la costrizione li mette in condizioni di moto circolare. Ed anche qui c’è l’intervento divino:

 Questa regola poggia sullo stesso fondamento delle altre due e dipende solo dal fatto che Dio conserva ogni cosa mediante un’azione continua, quindi, non come può essere stata un po’ prima, ma esattamente com’è nell’istante in cui la conserva. Ora, il movimento rettilineo è il solo che sia perfettamente semplice e la cui natura sia completamente contenuta in un istante. Infatti per concepirlo basta pensare un corpo in azione per muoversi verso una certa direzione, il che si verifica in ognuno degli istanti determinabili nel tempo in cui si muove. Mentre, per concepire il movimento circolare, o un altro qualunque movimento, bisogna considerare almeno due dei suoi istanti, o meglio due delle sue parti, e il loro mutuo rapporto.  Ma perché i filosofi, o meglio i sofisti, non trovino qui un’occasione all’esercizio delle loro sottigliezze superflue, osservate che io non affermo con 9-uesto che il movimento rettilineo possa avvenire in un istante; dico solo che tutti i requisiti necessari a produrlo si trovano nei corpi in ogni istante determinabile nel loro movimento; mentre non vi si trovano tutti i requisiti necessari a produrre il moto circolare [Monde; 14; 68]

        Questo passo è evidentemente contorto e lo stesso Descartes se ne rende conto, tentando di esemplificarlo con l’esempio di una fionda.

Se, per esempio, un sasso si muove in una. fionda secondo il cerchio AB (vedi figura), e lo considerate esattamente com’è nell’istante in cui arriva al punto A, trovate che esso è in azione per muoversi, infatti non ci si arresta, e per muoversi in una certa direzione, ossia verso C, infatti, in quest’istante, il suo movimento è determinato in quella direzione; mentre non potreste scoprire nulla che determini il sasso a muoversi circolarmente. Tanto che, supponendo che cominci allora a uscire dalla fionda, e che Dio continui a conservarlo com’è in quell’istante, per certo non lo conserverà con l’inclinazione a muoversi circolarmente secondo la linea AB, ma con quella di andare diritto verso il punto C.

Secondo questa regola dunque dobbiamo dire che solo Dio è l’autore di tutti i movimenti che sono al mondo, in quanto sono e in quanto sono rettilinei; mentre a renderli irregolari e a curvarli sono le diverse disposizioni della materia. Allo stesso modo i teologi c’insegnano che Dio è l’autore di tutte le nostre azioni, in quanto sono, e in quanto sono in qualche misura buone, mentre sono le diverse disposizioni della nostra volontà che possono renderle viziose [Monde; 14; 68-69]

        Non c’è dubbio che questa esposizione è contorta e non posso fare a meno di pensare alla limpidezza didattica di Galileo. Queste spiegazioni spiegano poco e noi possiamo capire solo perché conosciamo un poco di fisica. Descartes sta dicendo che dinamicamente, nel punto A, se si rompe il vincolo, il sasso se ne va per la tangente verso C piuttosto che verso B. Ma la cosa è complessa ed impegna molto Descartes tanto che ci ritornerà nel capitolo XIII del Mondo e nella Parte III dei Principia con medesimi ragionamenti ed altri due esempi⁽³⁾. Il problema è che Descartes si rende conto che vi sono altre forze che agiscono sul sistema fionda-sasso. Ad esempio, la fionda risulta in tiro mentre viene fatta ruotare e questo tiro appare come se vi fosse una forza perpendicolare a quella tangente di prima. In definitiva nel fenomeno che osserviamo appaiono esservi tre moti: quello circolare che porta il sasso da A a B; quello rettilineo che interviene quando cessa il vincolo che porta il sasso da A a C; quello rettilineo che lo farebbe muovere lungo il raggio DA, verso E. Quanto ho riassunto Descartes, con una prosa ancora contorta (per rendere conto dei moti celesti ed in particolare assimilando l’aria al sasso), lo dice così (capitolo XIII):

[…] il sasso che ruota in una fionda secondo il circolo AB (vedi figura precedente), quando si trova in A, tende verso C, se si  considera solo la sua agitazione, prescindendo dal resto; tende circolarmente da A verso B, se si considera il suo movimento in quanto regolato e determinato dalla lunghezza della corda che lo trattiene; infine, il medesimo sasso tende verso E se, prescindendo da quella parte della sua agitazione il cui effetto non è impedito, si oppone l’altra parte alla resistenza che la fionda le offre di continuo.

Ma per capire chiaramente l’ultimo punto, immaginate l’inclinazione del sasso a muoversi da A verso C come fosse la risultante di altre due inclinazioni: una a ruotare secondo il circolo AB, l’altra a salire perpendicolarmente secondo la linea VXY; e ciò in proporzione tale che il sasso trovandosi nel punto V della fionda, quando la fionda è nel punto A del cerchio, deve trovarsi poi in X quando la fionda sarà verso B, e in Y, quando la fionda sarà verso F, restando così sempre nella linea retta ACG. Quindi, sapendo che una parte della sua inclinazione, quella cioè che lo porta a seguire il cerchio AB, non è per nulla ostacolata dalla fionda, vi sarà facile vedere che trova resistenza soltanto per l’altra parte, cioè per quella che, se non fosse ostacolata, lo farebbe muovere secondo la linea DVXY; e, in conseguenza, il sasso tende – cioè dirige il proprio sforzo – solo ad allontanarsi direttamente dal centro D. E notate che, secondo questa considerazione, trovandosi nel punto A, esso tende davvero verso E, a tal segno da non essere affatto più disposto a muoversi verso H che verso I, anche se, tralasciando di considerare la differenza tra il movimento che esso ha già e l’inclinazione a muoversi che gli resta, ci si potrebbe persuadere facilmente del contrario [Monde; 14; 102-103]

        Osserva Shea che Descartes ha in mano il moto circolare ma non riesce a tirarlo fuori con chiarezza combinando le prime due regole che ha enunciato. Inoltre, se si fa riferimento a quanto ho risaltato dello scritto precedente, sembra che le due regole saltino. Sembra cioè che Descartes consideri il moto circolare come inerziale. A questo punto interviene anche il grande studioso della fisica del Sei-Settecento, Richard S. Westfall, che dice: “Descartes tornava, senza rendersi conto, ad abbracciare di fatto l’idea del moto circolare come moto naturale“. Aggiungendo poi: “Pur se il moto circolare cessò di rappresentare per Descartes il moto perfetto, continuò ad avere un ruolo centrale nella sua filosofia della natura. Anche non essendo naturale, esso era tutta via necessario” [Westfall; 28; 47]. Sia Shea che Westfall dicono che Descartes credeva nel moto circolare alla base del suo universo come un qualcosa che se pure non era completamente inerziale, lo era de facto. Il trattarlo con la matematica non avrebbe risolto questa ambiguità. Ma una cosa può essere evidenziata. La supposta conservazione della quantità di moto della quale ho detto risultava incompleta proprio nel punto che interessa il moto circolare. Lì era sottinteso con chiarezza che i cambiamenti di direzione non comportavano variazioni di quantità di moto e quindi dentro l’inerzia su una retta può entrare quella circolare. Diciamo che serviranno i lavori (sistemi di riferimento, forze centrifughe e centripete) di Huygens prima e di Newton poi per fare chiarezza su queste problematiche di grande rilievo. Descartes tornerà sulla questione, come accennato, nei Principia. Qui è interessato a sostenere la superiorità del suo Metodo nell’affermare che egli ha presente le cose da approfondire:

Oltre le tre leggi da me spiegate, non voglio supporne altre all’infuori di quelle che derivano necessariamente dalle verità eterne che i matematici prendono come fondamento abituale delle loro dimostrazioni più certe ed evidenti: parlo delle verità secondo cui Dio stesso ci ha insegnato di avere ordinato tutte le cose in base a numero, peso e misura; la loro conoscenza è talmente connaturata all’anima nostra che, quando le concepiamo distintamente, non potremmo negarne l’immancabile validità, né ammettere che se Dio avesse creato più mondi, esse non sarebbero in tutti altrettanto vere quanto nel nostro. Sicché chi saprà esaminare a sufficienza le conseguenze di tali verità e delle nostre regole potrà conoscere gli effetti dalle cause; e, per usare i termini della Scuola, potrà avere dimostrazioni a priori di tutto ciò che può essere prodotto in questo nuovo mondo.

E perché non vi siano eccezioni a fare ostacolo, aggiungiamo pure, se volete, alle nostre supposizioni che nel nuovo mondo Dio non farà mai miracoli, e che le intelligenze o anime ragionevoli che in seguito potremo supporvi non turberanno in nessun modo il corso ordinario della natura.

Con questo, tuttavia, non vi prometto di offrirvi dimostrazioni esatte di tutte le cose che dirò; basterà  se vi aprirò la strada perché possiate trovarle da voi stessi, quando vi impegnerete a cercarle. La mente, per lo più, perde il gusto delle cose presentate in modo troppo facile; e per comporre un quadro che vi risulti attraente, oltre ai colori vivi, devo impiegare anche l’ombra. Mi contenterò dunque di proseguire la descrizione iniziata come se mi proponessi soltanto di raccontarvi una favola  [Monde; 14; 70]

        Dopo essersi fatto di nuovo portavoce di Dio spiegandoci che, una volta che il mondo è in marcia, Egli non interverrà più, Descartes continua ad affidare le difficoltà ai lettori che dovranno sviluppare le cose che egli ha iniziato.

1.6 – La formazione del Sole ed i vortici

        A questo punto Descartes ha in mano tutti i prerequisiti che gli servivano per la descrizione del funzionamento del suo universo cosa che fa nel capitolo VIII del Mondo.

        Dio, dal caos iniziale, ha poi creato uno spazio coincidente con una materia, assimilabile al corpo più duro e solido del mondo. Come ho già detto, questo passaggio non si capisce perché, subito dopo, ci viene detto che, poiché sarebbe stato impossibile muovere tale corpo (e ciò in accordo con la definizione dei tre elementi), il moto deve essere iniziato da qualche parte e poi essersi diffuso ovunque. Insisto nel dire che la cosa detta così non si capisce risultando addirittura in contrasto con quanto detto qualche riga più su dove è scritto che, qualunque sia il caos che Dio ha organizzato nella materia del mondo, in seguito, in base alle leggi da lui imposte alla natura, quasi tutte queste parti di materia, devono aver preso la forma del secondo elemento e cioè quella di particelle rotonde assimilabili alle particelle di aria o di un fluido. Se avesse posposto i due periodi (prima il caos, poi il blocco unico di materia, infine una qualche rottura con un primo pezzo in moto …) la cosa sarebbe stata più comprensibile anche se non del tutto perché incombe sempre quel pezzo di materia solida e dura (credo si possa qui avanzare l’ipotesi che in Descartes vi è il pregiudizio di materia e spazio coincidenti ed egli non riesca a pensare, almeno da un certo punto, uno spazio frantumato in particelle, anche se pieno). Provo comunque a ridire il tutto come normalmente è raccontata la concezione cartesiana dell’universo.

        Si parte da un tutto pieno costituito da infinite particelle. Una particella ha iniziato a muoversi (Dio ?) e, poiché vi è un tutto pieno, il moto non ha potuto far altro che stendersi all’insieme di tutta la materia: la prima particella per muoversi ha spinto la seconda, che a sua volta … finché tutte le particelle sono entrate in movimento. E come è possibile conciliare il tutto pieno con il tutto in moto ? Solo con il moto vorticoso (si pensi ad una maionese). Di modo che l’intero universo è costituito da infiniti vortici come cercherò di descrivere seguendo il Mondo ed aiutandomi con la figura che ci viene offerta.

Dice Descartes:

L’uniformità della materia, d’altra parte, non ha potuto essere proprio perfetta. In primo luogo, non esistendo nel nuovo mondo alcun vuoto, è impossibile che tutte le parti della materia si siano mosse in linea retta; ma, essendo a un dipresso uguali e potendo esser tutte deviate press’a poco con la stessa facilità, hanno dovuto accordarsi tutte quante nel movimento circolare. Tuttavia, poiché supponiamo che Dio le abbia mosse in origine in maniere diverse, non dobbiamo ritenere che si siano messe a girare tutte intorno a un unico centro, bensì intorno a parecchi centri diversi che possiamo immaginare in situazioni reciproche diverse  [Monde; 14; 71]

         A seguito quindi di disomogeneità della materia già ridotta a pezzi istantaneamente, il moto è divenuto vorticoso e policentrico come appunto mostra la figura e si sarà organizzato in modo che le particelle più piccole sono verso i centri del moto e le più grandi verso l’esterno del vortice (esse hanno dovuto essere meno agitate o più piccole, o l’una e l’altra cosa insieme, verso i luoghi più vicini a questi centri che non verso i luoghi più lontani). Ciò è spiegato con il fatto che le particelle più grandi avevano maggiore tendenza delle altre al moto rettilineo e quindi si sistemavano su cerchi più grandi perché di più si approssimano alla linea retta. La materia, in moto vorticoso, deve poi aver subito cambiamenti ed essere passata da una primitiva grande differenziazione in parti di varie grandezze e forme con tendenze a muoversi in tutti i modi e direzioni o a restare ferme. Ma poi tutte le parti di materia

devono essere diventate press’a poco tutte uguali, specialmente quelle che sono rimaste alla medesima distanza dai centri intorno a cui ruotavano. Infatti, non potendo muoversi le une senza le altre, le più agitate hanno dovuto comunicare parte del loro movimento a quelle che lo erano meno, e le più grandi hanno dovuto spezzarsi e dividersi per poter passare per i medesimi luoghi di quelle che le precedevano, oppure salire più in alto; così, in breve tempo, hanno raggiunto tutte una disposizione ordinata, in modo che ognuna si è venuta a trovare più o meno lontana dal centro intorno a cui aveva preso a muoversi a seconda che era più o meno grande, più o meno agitata in rapporto alle altre. Anzi, dato che la grandezza è sempre in contrasto con la velocità del movimento, è da ritenere che le più lontane da ciascun centro siano state quelle che essendo un po’ più piccole delle più vicine, erano anche parecchio più agitate  [Monde; 14; 72-73]

        E qui, a me sembra che Descartes dica esattamente l’opposto di quanto ha detto qualche riga più su ma la cosa non deve stupire perché in Descartes accade spesso. Comunque in questo modo si è arrivati alla differenziazione dei tre elementi che Descartes ha definito nel capitolo V. Attraverso una continua opera di strofinio alcuni pezzi di materia primordiale sono diventati piccole palline costituenti il secondo elemento, l’aria, altri pezzi, che dovevano sistemarsi ed adattarsi negli interstizi di queste prime particelle, erano diventati più piccoli e più veloci dei precedenti per doversi infilare rapidamente attraverso passaggi molto stretti in ogni anfrattino (ma anche senza forma perché dovevano adattarsi alle forme libere preesistenti) ed hanno originato il primo elemento, il fuoco, altri pezzi infine, che fin dall’inizio erano i pezzi più grandi, hanno resistito di più alla frantumazione, si muovono più piano e costituiscono il terzo elemento, la terra. E qui Descartes organizza i suoi tre elementi in modo che possano produrre la luce:

E un’altra cosa va rilevata: quanto del primo elemento [il fuoco, ndr] si trova in eccedenza rispetto allo spazio dei piccoli intervalli da riempire che le parti del secondo elemento, essendo rotonde, lasciano necessariamente intorno a sé, deve ritirarsi verso i centri intorno a cui queste ruotano, perché esse occupano tutti i luoghi più distanti; e là deve comporre dei corpi rotondi, perfettamente fluidi e sottili, che ruotando senza posa molto più velocemente, ma nello stesso senso delle parti del secondo elemento da cui sono circondati, hanno la forza di aumentare l’agitazione delle più vicine; e persino di spingerle tutte da ogni lato, dal centro alla circonferenza, in modo che si spingano anche l’una con l’altra. Il tutto per mezzo di un’azione che ora dovrò spiegare quanto più esattamente potrò. Infatti vi dico ora in anticipo che, secondo me, questa azione è la luce, e che i corpi rotondi composti della materia del primo elemento nella sua assoluta purezza sono l’uno il Sole e gli altri le stelle fisse del nuovo mondo che vi sto descrivendo; infine, identifico coi cieli la materia del secondo elemento che gira intorno al Sole e alle stelle fisse  [Monde; 14; 74]

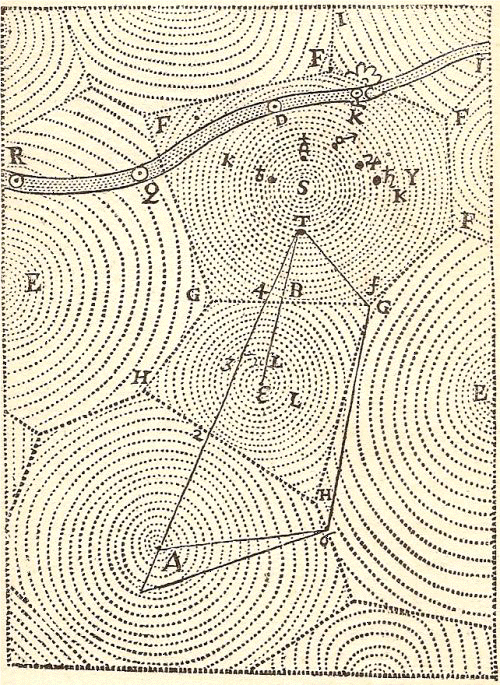
        Vi è qui l’impegno di spigare bene questa costruzione che fin dall’inizio appare complessa. Se da una parte è possibile descrivere un vortice materiale con la dinamica dei pezzi che lo compongono da osservazioni empiriche, risulta più complesso spiegare il perché il Sole, con la mole che ha, debba stare al centro di un vortice. Descartes comunque parla di corpi rotondi, perfettamente fluidi e sottili e probabilmente questa sottigliezza glielo permette fermo restando che si origina una nuova separazione aristotelica tra i corpi celesti (Sole formato dal primo elemento e terra e pianeti dal terzo) che non risultano più tutti della stessa natura come altri scienziati del Seicento con fatica stavano mostrando. Inoltre, quando verrà a sapere della scoperta delle macchie solari dalle quali si ricavava la lenta rotazione del Sole rispetto ai pianeti, modificherà quanto qui dice e lo scriverà nei Principia con una spiegazione che, se possibile, è più insoddisfacente di quanto non lo sia quella esposta nel Mondo (intorno al Sole deve esservi un’atmosfera estendentesi fino a Mercurio, che rallenta le macchie solari!). Ma, tornando alla luce, dice Descartes:

Poniamo, per esempio (vedi figura precedente), che i punti S.E.e.A siano i centri di cui parlo; e che tutta la materia inclusa nello spazio F.G.G.F. sia un cielo ruotante attorno al Sole indicato con S; e che tutta quella dello spazio H.G.G.H. sia un altro cielo ruotante intorno alla stella indicata con E, e così via: in modo che vi siano tanti cieli diversi quante sono le stelle; ma, essendo indefinito il numero delle stelle, altrettanto diciamo del numero dei cieli; e che il firmamento altro non sia se non la superficie priva di spessore che separa tutti i cieli gli uni dagli altri  [Monde; 14; 75]

Osservate infine che, stando a quanto ho detto sul modo di formarsi del Sole e delle altre stelle fisse, i loro corpi possono essere così piccoli rispetto ai cieli dove sono contenuti, che anche tutti i circoli KK,LL, e simili, che indicano fin dove la loro agitazione fa giungere il corso della materia del secondo elemento, si ridurranno, in confronto ai cieli, a punti che ne indicano il centro. Sì che gli astronomi moderni considerano quasi come un punto, in rapporto al firmamento, l’intera sfera di Saturno [Monde; 14; 77]

        E’ qui importante notare che la teoria dei vortici aiuta molto Descartes nella sua continua volontà di non dispiacere alla Chiesa. Egli era certamente un copernicano ma nessuno avrebbe potuto accusarlo di aver assegnato un qualche moto ad una Terra che risultava nella sua rotazione diurna intorno al proprio asse,  solo trascinata dal vortice della materia celeste che la circonda e poiché essa non è in moto rispetto a tale vortice, risulta immobile, pur essendo in rotazione.
 

1.7 – Pianeti, comete e satelliti

        Vediamo allora la costituzione dell’universo di Descartes con particolare riferimento al sistema solare. Dai moti iniziali, pian piano si sono costituiti vari vortici contigui (quelli con centri S.E.e.A), ognuno dei quali è un sistema in rotazione intorno ad una stella. Il nostro sistema, quello solare, è indicato in figura con il vortice che ha S come centro. I pianeti sono trascinati in moto dalle piccole particelle sferiche che costituiscono il secondo elemento. Le piccole sfere che si trovano al bordo esterno del vortice (quelle che sono negli F) si muovono più in fretta e la loro velocità diminuisce gradualmente di modo che esse sono spinte più verso il centro del vortice, nella zona cui compete minore velocità che è quella di Saturno (KK). Qui tali particelle sono diventate più piccole e veloci per rendere conto della minore velocità di Saturno rispetto a Mercurio (più vicino al Sole), anche se non si capisce perché la velocità di tali particelle debba cambiare così radicalmente. E la maggior velocità dei pianeti vicini al Sole risulta spiegata da una sorta di agitazione che lo stesso Sole trasferirebbe loro. Il ruolo dei corpuscoli, è anche un altro, come Descartes ci dirà nei Principia: se qualche pianeta non ce la facesse più nel suo moto intorno al Sole e tendesse a scendere, incontrerebbe particelle più piccole, in grado di circondarlo e di ridargli impulso; al contrario, se qualche pianeta volesse salire verso luoghi più lontani dal Sole, troverebbe corpuscoli più grandi e tali da rallentarlo per riportarlo in basso. Tali corpuscoli regolano quindi la stabilità del sistema. Vi sono poi da considerare le comete che sono blocchi del terzo elemento che sfuggono a causa del loro movimento circolare che tende ad essere più ampio di quello che quel vortice permette. E così le comete vanno da vortice a vortice come quella mostrata nella figura precedente che segue la rotta CDQR. Queste ed altre cose che cercherò di riassumere, sono discusse da Descartes tra i capitoli  IX e XI del Mondo e furono integrate da altre considerazioni e figure che compaiono nei Principia.

        Le argomentazioni di Descartes ci dicono che l’aggregazione di corpuscoli di terra è avvenuta nel tempo. Tali corpuscoli, più grandi e meno mobili, hanno trovato più facile riunirsi che non spezzarsi ancora ed in tal modo hanno costituito i grandi corpi che si muovono dentro i corpuscoli del secondo elemento trascinati da queste ultime. Il fenomeno avviene come dei battelli sono trascinati dalla corrente di un fiume che, se si fa attenzione, si osserva che più sono massicci, più sono trascinati con foga. Si pensi ad un grande battello che si muove veloce ed a quella schiuma che invece si muove pigramente (rilevante qui è il fatto che che non si fa cenno alla resistenza che invece i pianeti dovrebbero incontrare nel loro moto in mezzo ai corpuscoli del secondo elemento dato che corpuscoli e pianeti non si muovono alle medesime velocità). Inoltre, se avessimo due fiumi che mescolano ad un certo punto le due correnti in modo di aver in un dato punto una corrente maggiore delle singole, i corpi massicci, come i battelli, trascinati da uno dei due fiumi, hanno la capacità di infilarsi nell’altro, mentre

quelli leggeri ne sono respinti (la cosa si può osservare empiricamente con un solo fiume che separa le sue acque in correnti di diversa intensità, ndr). Ed è questo il modo in cui si comportano le comete: alcune aggregazioni di corpuscoli, né del primo né del secondo elemento, trovatesi nel punto più esterno del vortice possono o mettersi in circolo e costituire i pianeti o transitare verso altro vortice originando le comete. Riguardo a queste ultime devono essere rimaste in poche nel sistema solare perché, da quando si sono create, devono essere andate distrutte quasi tutte a seguito dei continui urti che subiscono nel transito ad altro vortice. E, dopo aver discusso in modo confuso le posizioni della visibilità della cometa, della chioma della medesima e della direzione che essa assume, Descartes passa a discutere dei pianeti. con le cose che ho già detto alle quali occorre aggiungere il fatto che i corpuscoli del secondo elemento, oltre a far girare i pianeti intorno al Sole, devono provvedere a due fatti:

1) far girare i pianeti su se stessi e comporre intorno ai pianeti dei piccoli cieli che si muovono nello stesso senso del cielo più grande;

2) se due pianeti di diversa grandezza, sono disposti originariamente alla medesima distanza dal Sole, il più piccolo dei due, muovendosi più velocemente dell’altro, dovrà unirsi al piccolo cielo che circonda il pianeta più grande e girare continuamente intorno ad esso.

        Qui siamo in grado di capire cos’è il piccolo cielo e a cosa serve questa costruzione a Descartes: egli vuol trovare sistemazione nel cielo di pianeti come la Luna. E, data la premessa ora letta, la spiegazione del satellite Luna viene spiegata nel modo seguente:

Infatti, poiché le parti del cielo che si trovano, per esempio, verso A (vedi figura), si muovono più veloci del pianeta indicato con T, che

spingono verso Z, evidentemente devono, a loro volta, esser deviate dal pianeta T e costrette a volgere il loro corso verso B [Monde; 14; 88]

        Descartes sta qui dicendo che la Terra si muove più lentamente dei corpuscoli del secondo elemento dentro cui è immersa. Quando tali corpuscoli arrivano ad A sono deviati verso B

Dico verso B piuttosto che verso D, perché, avendo inclinazione a continuare il loro movimento in linea retta, devono andare verso l’esterno del cerchio ACZN che descrivono piuttosto che verso il centro S. Ora, passando così da A verso B, obbligano il pianeta T a girare con esse intorno al proprio centro; e, reciprocamente, il pianeta, girando così, dà loro occasione di avviare il loro corso da B verso C, poi verso D e verso A, formandogli intorno un cielo particolare, con cui esso deve in seguito continuare a girare, dalla parte chiamata Occidente a quella chiamata Oriente, non solo intorno al Sole, ma anche intorno al proprio centro [Monde; 14; 88-89]
 

        Ora, secondo Descartes, la Luna occupa la stessa zona della Terra, solo che ha maggiore velocità perché è più piccola ed anche essa subirà una deviazione verso B quando sarà arrivata ad A ed entrerà nel vortice che circonda la Terra.

Inoltre, sapendo che il pianeta indicato con una piccola falce è disposto ad avviare il proprio corso secondo il circolo NACZ come il pianeta T, di cui deve muoversi più velocemente perché più piccolo, è facile capire che, in qualunque luogo del cielo si trovasse all’inizio, ha dovuto in breve andare a collocarsi contro la superficie esterna del piccolo cielo ABCD e che, dopo essersi ad esso congiunto, deve poi sempre continuare con le parti del secondo elemento che sono verso questa superficie il proprio corso intorno a T  [Monde; 14; 90]

        A questo punto, visto che è tutto chiaro, Descartes non si sofferma sugli altri pianeti che circondano Saturno o Giove ma chiude il capitolo al solito modo:

Non mi propongo di dire tutto e ho parlato in particolare di questi due solo per rappresentarvi col pianeta T la Terra che abitiamo, e col pianeta indicato con una piccola falce la Luna che le gira intorno [Monde; 14; 91]

1.8 – Il peso

        La teoria dei vortici, per Descartes, è esplicativa di tutto. Le fantasie che vorrebbero l’attrazione dei corpi come proprietà della materia vengono respinte. La materia non ha alcuna proprietà, in particolare l’effetto del peso gli proviene dalle proprietà dei vortici e da quella della forza centrifuga. A queste spiegazioni Descartes dedica varie pagine molto confuse nel capitolo XI del Mondo.

        Intorno alla Terra vi è un vortice secondario, o piccolo cielo, che corre più veloce della medesima Terra e quindi ha una forza centrifuga maggiore. Se sulla Terra lasciamo andare una pietra essa avrà velocità minore delle particelle del secondo elemento che costituiscono il vortice secondario e quindi non potrà essere mantenuta in alto ma sarà sbattuta in basso, sulla medesima Terra. E questo accadrà per ogni corpo grande che non sarà in grado di acquistare la velocità dei corpuscoli del secondo elemento che circondano la Terra. Qui, e Descartes se ne rende conto, vi è un’ennesima contraddizione con quanto egli ha detto sulle comete che, dal bordo del vortice, possono trasmigrare in altri vortici. Egli ci dice semplicemente che alcuni corpi solidi possono acquistare una velocità di discesa tale che superano il centro per  arrivare fino al limite del vortice da dove potranno comportarsi da comete. Basta così.

Desidero ora richiamare la vostra attenzione sulla pesantezza della Terra, ossia sulla forza che ne unisce tutte le parti facendole tendere verso il centro, ciascuna in proporzione della propria grandezza e solidità. Questa forza consiste solo nel fatto che le parti del piccolo cielo che circonda la Terra, girando attorno al suo centro molto più rapidamente delle sue, tendono anche ad allontanarsene con più forza e quindi a respingere le sue verso il centro stesso. Se ci trovate qualche discrepanza con quanto ho detto poc’anzi – che i corpi più massicci e solidi, come ho immaginato le comete, si avviavano verso le circonferenze dei cieli, mentre gli altri soltanto erano respinti verso il centro – quasi dovesse conseguirne che solo le parti meno solide della Terra possano essere spinte verso il suo centro, mentre le altre devono allontanarsene, tenete presente che, quando ho parlato della tendenza dei corpi più solidi e massicci ad allontanarsi dal centro di un cielo, li ho supposti già in precedenza in movimento all’unisono con la materia di tale cielo. Infatti, certamente, se ancora non hanno cominciato a muoversi, o se si muovono più lentamente di quanto occorre per seguire il corso di quella materia, devono, in primo luogo, venirne cacciati verso il centro intorno a cui essa gira, ed è anche certo che, quanto più grandi e solidi sono, tanto più forte e rapida sarà la spinta. Cionondimeno, se sono abbastanza grandi e solidi da formare delle comete, potranno poco dopo avviarsi verso le circonferenze esterne dei cieli; poiché l’agitazione acquisita scendendo verso qualcuno dei loro centri li renderà immancabilmente capaci di passar oltre e di risalire verso la circonferenza  [Monde; 14; 92-93]

       Mersenne, come ricorda Shea, si mostrò insoddisfatto e gli chiese spiegazioni. Descartes rispose con un’esperienza (qualitativa) che aveva realizzato. Se si sistemano in una bacinella con dell’acqua dei pezzi di legno e piombo e si mette il tutto in rotazione si osserva che i pezzi di piombo spingono verso il centro i pezzi più leggeri allo stesso modo che la materia spinge i corpi terrestri. A questa osservazione empirica c’è solo da rispondere (con Aiton 1972, citato da Shea) che non rispetta l’analogia richiesta in quanto piombo e legno della bacinella hanno stesse velocità mentre i pezzi di materia e i corpuscoli del secondo elemento sulla Terra hanno velocità molto diverse. Inoltre si deve tener conto di tante altre questioni come i vortici ulteriori che mettono in moto i pezzi di legno nella bacinella.

        Descartes, comunque, fa svariati ragionamenti per convincerci della sua teoria della pesantezza che sono davvero poco interessanti per il fine che mi sono proposto. Può comunque concludere il capitolo ritenendo che la sua teoria della pesantezza sgombera il campo dalle obiezioni che i peripatetici facevano al moto della Terra:

Di qui potete intendere che le ragioni addotte da parecchi filosofi per negare il movimento della vera Terra non hanno valore contro quello della Terra che vi descrivo. Come quando affermano che, se la Terra si muovesse, i corpi pesanti non dovrebbero scendere a piombo verso il suo centro, ma piuttosto scostarsene di qua e di là verso il cielo; e che i cannoni puntati ad Occidente dovrebbero arrivare con la loro portata molto più lontano di quelli puntati a Oriente; e che nell’aria si dovrebbero sentir sempre di gran venti e di gran rumori; e simili cose che si possono sostenere solo supponendo la Terra, anziché trascinata dal corso del cielo che la circonda, mossa da qualche altra forza in senso diverso da questo cielo [Monde; 14; 97].

1.9 – Le maree

        Dice Descartes riferendosi alla figura seguente:

Considerate la Terra EFGH, con l’acqua 1, 2, 3, 4 e l’aria 5, 6, 7, 8, che, come vi dirò in seguito, si compongono di alcune delle parti meno solide della Terra con cui formano un’unica massa. Considerate poi anche la materia del cielo, che riempie, non solo lo spazio fra i cerchi ABCD e 5, 6, 7, 8, ma anche tutti i piccoli interstizi che sono al disotto, fra le parti dell’aria, dell’acqua e della terra. E tenete presente che, girando insieme questo cielo e questa Terra attorno al centro T tutte le loro parti tendono ad allontanarsene ma quelle del cielo con molta più forza rispetto a quelle della terra, perché sono molto più agitate; e, fra le parti della Terra, tendono ad allontanarsene di più le più agitate verso la stessa direzione delle parti, del cielo [Monde; 14; 93-94].

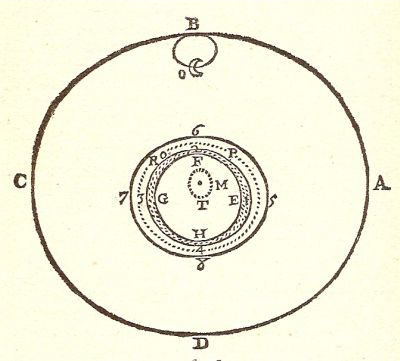
        Consideriamo ora la Luna, indicata con il cerchio in alto OB, e supponiamola immobile rispetto al punto B in confronto alla velocità che ha la materia del cielo che sta sotto di essa. Dice Descartes:

considerate che questa materia del cielo, avendo fra O e 6 un passaggio più stretto di quello che avrebbe fra B e 6 (se la Luna non occupasse lo spazio fra O e B), e dovendocisi quindi muovere un po’ più rapidamente, deve senz’altro avere la forza di spingere un po’ la Terra verso D, in modo che il suo centro T, come vedete, si allontani un poco dal punto M che è il centro del piccolo cielo ABCD: infatti, a sostenerla dov’è, c’è solo la materia di questo cielo. E poiché l’aria, 5, 6, 7, 8, e l’acqua, 1, 2, 3, 4, che circondano la Terra sono corpi fluidi, evidentemente, la stessa forza che preme la Terra a questo modo deve farli scendere verso T, non solo dal lato 6, 2, ma anche dal lato opposto 8, 4, e, in compenso farli salire nei luoghi 5, 1 e 7, 3; così, mentre la superficie della Terra EFGH, essendo dura, resta rotonda, quella dell’acqua 1, 2, 3, 4, e quella dell’aria 5, 6, 7, 8, essendo fluide, devono assumere forma ovale [Monde; 14; 98]

        Secondo Descartes il fenomeno delle maree trae origine da quella strettoia che la presenza della Luna provoca nella parte superiore del vortice secondario, tra O e 6. La materia celeste in rotazione si muove più in fretta in questa strettoia e deprime l’aria e l’acqua in 6 e 2 e, con questo, spinge la terra dal centro M del vortice verso il basso fino ad una nuova posizione T. Ciò vuol dire che l’intera Terra si sposta dalla sua posizione avvicinandosi a D lasciando meno spazio al passaggio della materia celeste tra 8 e D. Ciò provoca la depressione di aria ed acqua in 8 e 4 ed in 6 e 2. In definitiva la superficie dell’acqua si schiaccerà in 6, 2 e in 8,4 e si rigonfierà in 7, 3 e 5, 1. Basta considerare che la Terra fa un giro completo su se stessa in 24 ore per comprendere come si sposta il rigonfiamento dell’acqua e la conseguente depressione e quindi rendere conto del ciclo giornaliero delle alte e basse maree che si succedono ogni 12 ore. Poiché poi la Terra ruota su se stessa in senso antiorario andando da ovest ad est, il rigonfiamento si muoverà in direzione opposta.

        Per spiegare il ciclo mensile  delle maree Descartes considera che la Luna si muove nella stessa direzione della Terra completando in un mese la rivoluzione facendo si che in sei ore descrive un centoventesimo della sua orbita. E questo origina i fenomeni ciclici di ritardo di 50 minuti giornalieri della marea che si osservano. Per spiegare poi le alte maree con Luna piena e nuova e le basse maree con i quarti di Luna (ciclo semi mensile) Descartes introduce una nuova proprietà dei vortici tale che il vortice non risulta perfettamente sferico ma ovale, con l’asse BD più corto di CA. Ciò comporta che la Luna vada più veloce in B e D (Luna piena e nuova) rispetto a C ed A (quarti di Luna). Il ciclo annuale delle maree viene invece affrontato solo nei Principia.

1.10 – La luce

        Ricordo che il titolo completo dell’opera di Descartes che discutiamo è: Traité du Monde o Traité de Lumière (ed ha come ultimo capitolo il Traité de l’Homme). Ciò vuol dire che Descartes assegnava pari importanza alla luce di quanta non ne avesse assegnata a ciò che ho discusso fin qui, anche se la sua discussione occupa solo i capitoli XIII e XIV.

        Nell’iniziare questo argomento, Descartes ha ben presente quanto aveva sostenuto o stava sostenendo nella Dioptrique. Egli parte da quanto aveva iniziato a dire all’inizio della sua teoria dei vortici, quando si era occupato di moto circolare e di tendenza dei corpi dotati di moto circolare di allontanarsi dal centro del moto. Si tratta ora di capire verso quali direzioni tendono le parti di materia di cui si compongono il cielo e gli astri. Il problema è sciogliere effetti che si sommano poiché spesso cause diverse si trovano ad agire contemporaneamente sul medesimo corpo, in modo che una annulla l’effetto sull’altra, in base a diverse considerazioni si può affermare che uno stesso corpo tende contemporaneamente verso direzioni diverse.

Ed a questo punto interviene quanto ho già anticipato in 1.5, come esemplificazione di quanto or ora sostenuto  e che riporto per comodità del lettore:

Così, per esempio, il sasso che ruota in una fionda secondo il circolo AB (vedi figura precedente), quando si trova in A, tende verso C, se si  considera solo la sua agitazione, prescindendo dal resto; tende circolarmente da A verso B, se si considera il suo movimento in quanto regolato e determinato dalla lunghezza della corda che lo trattiene; infine, il medesimo sasso tende verso E se, prescindendo da quella parte della sua agitazione il cui effetto non è impedito, si oppone l’altra parte alla resistenza che la fionda le offre di continuo.

Ma per capire chiaramente l’ultimo punto, immaginate l’inclinazione del sasso a muoversi da A verso C come fosse la risultante di altre due inclinazioni: una a ruotare secondo il circolo AB, l’altra a salire perpendicolarmente secondo la linea VXY; e ciò in proporzione tale che il sasso trovandosi nel punto V della fionda, quando la fionda è nel punto A del cerchio, deve trovarsi poi in X quando la fionda sarà verso B, e in Y, quando la fionda sarà verso F, restando così sempre nella linea retta ACG. Quindi, sapendo che una parte della sua inclinazione, quella cioè che lo porta a seguire il cerchio AB, non è per nulla ostacolata dalla fionda, vi sarà facile vedere che trova resistenza soltanto per l’altra parte, cioè per quella che, se non fosse ostacolata, lo farebbe muovere secondo la linea DVXY; e, in conseguenza, il sasso tende – cioè dirige il proprio sforzo – solo ad allontanarsi direttamente dal centro D. E notate che, secondo questa considerazione, trovandosi nel punto A, esso tende davvero verso E, a tal segno da non essere affatto più disposto a muoversi verso H che verso I, anche se, tralasciando di considerare la differenza tra il movimento che esso ha già e l’inclinazione a muoversi che gli resta, ci si potrebbe persuadere facilmente del contrario [Monde; 14; 102-103]

        Ciò che ora è stato detto per il sasso deve valere anche per i corpuscoli del secondo elemento che costituiscono la materia del cielo. Riferendoci alla figura seguente le particelle che, ad esempio, si trovassero vicine ad E, tendono ad andare verso P, ma la resistenza delle altre particelle del cielo che si trovano al di

sopra le fa andare lungo ER ma le sforza radialmente anche lungo EM (quest’ultimo effetto è dovuto in parte al vincolo esercitato dalla materia aldilà di E che frena le particelle celestiali come la fionda frena la pietra ed in parte dalla rotazione del Sole S ed in parte ancora dall’azione della materia interposta tra S ed E). In definitiva su E si esercita una pressione verso l’esterno e a tale pressione non contribuisce tutta la materia al di sotto della regione in cui si trova E, ma solo quella compresa nel cono AED e

la ragione che impedisce [all’altra materia situata al di sotto di E] di tendere verso questo spazio è che tutti i movimenti continuano, per quanto è possibile, in linea retta; quindi, quando la natura può prendere parecchie vie per giungere al medesimo effetto, segue sempre, immancabilmente la più breve [Monde; 14; 105-106]

e, in conseguenza di ciò, si avrà moto solo lungo linee rette cha dalla zona sottostante ad E vadano ad E. Quindi il modo più economico per la natura di riempire un supposto vuoto che si generi in E è che la materia contenuta nel cono AED salga andando ad occupare tale vuoto. Poiché vi è un’azione cumulativa di tanti corpuscoli su E, su E si esercita uno sforzo, come per cacciarlo dal suo posto. Gli altri corpuscoli poi, mentre avanzano verso E dalle zone più basse, sono soggetti a movimenti che non li lasciano mai nella stessa posizione toccandosi e separandosi subito dopo, continuando ad avanzare senza soluzione di continuità verso E fino al suo completo riempimento. Ed a questo punto Descartes introduce il tipo d’azione che origina la luce:

Da tutto ciò si può solo concludere che la forza con cui tendono verso E è una sorta di vibrazione che ora raddoppia d’intensità, ora diminuisce a piccole scosse in rapporto ai loro mutamenti di posizione: proprietà che appare molto confacente alla luce [Monde; 14; 111]

        In altre parole, le leggi del moto mostrano che, data la rotazione del Sole e della materia intorno ad esso, c’è una pressione radiale che dal Sole si propaga verso l’esterno lungo linee rette che si dipartono dal suo centro. Questa pressione si manifesta come una sorta di vibrazione, una proprietà che appare molto confacente alla luce.

       E, per dare una conclusione alla favola che Descartes ha detto di star raccontando, gli uomini del mondo fantastico descritto saranno di tale natura che, quando i loro occhi verranno spinti in questo modo, ne riceveranno una sensazione del tutto simile a quella che noi abbiamo della luce.

1.11 – Le proprietà della luce

        Da quanto abbiamo visto restano in sospeso almeno due importanti questioni. La prima è se questo modello è in grado di spiegare tutte le proprietà note della luce e la seconda è capire qual è la relazione esistente tra l’agitazione fisica della materia che origina uno stimolo agli occhi e la percezione della luce che noi abbiamo con i nostri occhi. La prima delle questioni la studierò ora, la seconda, affrontata da Descartes nel Traité de l’Homme che, come detto, è l’ultimo capitolo del Traité de Lumière, rientra in questioni di fisiologia che Descartes studiò in modo diffuso e delle quali io non mi occupo, come annunciato nella prima parte di questo lavoro.

        A proposito della prima questione posta, dice Descartes:

Le principali proprietà della luce sono: 1. Di diffondersi in cerchio da ogni lato attorno ai corpi detti luminosi. 2. A qualsiasi distanza. 3. Istantaneamente. 4. D’ordinario secondo linee rette che devono esser considerate i raggi della luce. 5. Parecchi di tali raggi, provenienti da punti diversi, possono raccogliersi in un punto solo. 6. Oppure, provenendo dallo stesso punto possono giungere a punti diversi. 7. O ancora, provenendo da punti diversi e andando verso punti diversi, possono passare per uno stesso punto senza ostacolarsi a vicenda. 8. Ma qualche volta possono anche ostacolarsi a vicenda, quando c’è tra loro grande disparità di forza, e quella degli uni è molto maggiore di quella degli altri. 9. Infine possono essere deviati per riflessione. 10. O per rifrazione. 11. E la loro forza può venire aumentata. 12. O diminuita dalle diverse disposizioni o qualità della materia che li riceve. Queste sono le principali qualità che si osservano nella luce; come vedrete, convengono tutte a quest’azione [Monde; 14; 113]

        Le prima proprietà per Descartesè ovvia in quanto la luce è prodotta dal moto circolare delle parti che la costituiscono. La seconda proprietà è altrettanto ovvia. Delle altre non parlo perché le ho o discusse altrove, quando ho commentato la Dioptrique, o sono questioni elementari di ottica geometrica che non richiedono attenzione particolare. La propagazione istantanea elencata al numero 3 è invece problematica e molto, anche per molte conseguenze che avrà. Per comprendere i ragionamenti di Descartes, anche relativamente alla propagazione rettilinea (che compare come questione 4), occorre ripensare alle analogie che egli aveva fatto a proposito della luce nella Dioptrique e cioè il cieco con il bastone e l’uva pigiata in un tino. Come devono essere sistemate le piccole sfere di materia celeste per render conto della propagazione rettilinea ? Prendiamo in considerazione la figura che Descartes ci presenta e quanto dice in proposito.

Quanto alle linee lungo le quali quest’azione si trasmette, che sono propriamente i raggi della luce, va notato che differiscono dalle parti del secondo elemento per mezzo delle quali l’azione stessa si trasmette: nel mezzo che attraversano i raggi non rappresentano nulla di materiale; indicano solo in che senso e secondo quale determinazione il corpo luminoso agisce. su quello illuminato; perciò vanno concepiti perfettamente rettilinei, anche se le parti del secondo elemento che servono a trasmettere l’azione, cioè la luce, non possono quasi mai collocarsi tanto esattamente l’una sull’altra da formare linee perfettamente rette. Come potete facilmente concepire che la mano A spinga il corpo E secondo la linea retta AE, anche se lo spinge solo per mezzo dell’estremità del bastone BCD che è storto; e che la sfera indicata con il numero 1 spinga quella indicata con 7 mediante le due indicate 5, 5, altrettanto direttamente quanto per mezzo delle altre sfere 2, 3, 4, 6 (vedi figura seguente) [Monde; 14; 115]

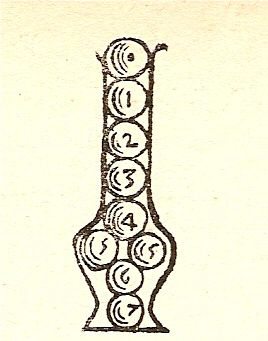
           A questo punto occorre fare riferimento a fatti occorsi a lato del Mondo. Nel 1634 l’ex amico di Descartes, Beeckman, si riappacificò per un breve periodo con il filosofo e lo andò a trovare ad Amsterdam. Fu qui che Descartes gli raccontò la sua teoria della luce e gli comunicò la necessità che aveva di sua propagazione istantanea. Beckmann fu scettico in proposito ritenendo che nulla di materiale può andare a velocità infinita. Propose un’esperienza a Descartes per determinare la velocità della luce ma Descartes non accettò e  fece riferimento ad un fatto naturale che tutti hanno visto e conoscono, le eclissi di Luna. Il conto a priori che faceva Descartes, assegnando alla luce una velocità che riteneva fantastica, era che la luce avrebbe dovuto impiegare circa un’ora per andare e tornare dalla Terra alla Luna (oggi sappiamo che tale tempo è minore di 3 secondi). Naturalmente Descartes diceva una sciocchezza che, ancora una volta, con i procedimenti scientifici non ha nulla a che vedere. Perché il suo conto avesse un senso compiuto sarebbe stato necessario conoscere prima la velocità della luce ma era ciò che si voleva trovare ! Detto meglio: come si può determinare il luogo esatto dello spazio in cui si trova la Luna quando la Terra inizia ad eclissarla ? Perché l’esperimento proposto da Descartes fosse significativo, sarebbe stato necessario disporre di un qualche sistema che gli permettesse di determinare in quale istante la Terra emette l’ombra che che eclissa la Luna, e ciò è il tipico discorso circolare perché non si può sapere se non si conosce la velocità della luce. Descartes diceva a Beeckman che era inutile fare l’esperimento che proponeva e Beeckman, che era uno scienziato, glie spiegava che i suoi argomenti evadevano la questione. Ma c’è dell’altro. La presunzione di Descartes era tanto grande che, quando Mersenne gli comunicò dell’esperimento che Galileo raccontava nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze a proposito della misura tentata e non riuscita della velocità della luce, riuscì solo a dire che quell’esperimento era inutile e che solo quello sulle eclissi era probante. Sta di fatto che il problema non fu mai risolto da Descartes che continuò a sostenere la velocità infinita della luce.

        Siamo arrivati alla fine della trattazione cartesiana della luce e ci resta solo da dire qualche parola sull’ultimo capitolo (il XV) nel quale Descartes, dalla favola, tenda di riportarci alla realtà.

        E la realtà è che da questo mondo e da quello si devono vedere le stelle cose. Ed il come debbano vedersi, Descartes lo ribadisce soffermandosi su alcuni punti che precedentemente non aveva trattato o non aveva approfondito. Qui, se possibile, la fantasia cavalca ancora di più per cui mi soffermo solo su alcuni aspetti d’interesse. Intanto ciascun vortice dell’universo appartiene ad una stella, come mostrato nella figura seguente:

Da: W.W. Rose, A Short Account of the History of Mathematics, 1908
 

        Da questo o da un altro mondo le stelle devono osservarsi in posizioni differenti da quelle che realmente occupano. Ciò accade perché, trovandosi in vortici differenti che hanno anche dimensioni diverse, nel passaggio da vortice a vortice devono subire rifrazioni (e qui Descartes accenna di nuovo alla Dioptrique). Inoltre può accadere che la medesima stella si vede più volte a seguito di sue successive riflessioni e rifrazioni. Infine le stelle, le cui superfici possono variare di forma e dimensioni a seguito del passaggio loro vicino di comete, trovandosi in materia fluida, devono ondeggiare ed oscillare ed è questo il motivo per cui le vediamo tremolanti.

        Con ciò si chiude il Traité du Monde o Traité de Lumière. Restano solo alcune mie considerazioni.

        Le cose che abbiamo visto mostrano con chiarezza che Descartes è persona in gran parte estranea alla scienza sperimentale così come si era venuta definendo con Galileo. Si potranno sfogliare le migliaia di pagine scritte da Galileo e mai si troverà un riferimento a Dio per la spiegazione di fatti naturali.

        Le elaborazioni di Descartes furono duramente criticate da Leibniz che, nel 1686, pubblicò un lavoro che fece molto discutere, Brevis demonstratio erroris memorabilis Cartesii. In esso Leibniz argomentò contro il meccanicismo cartesiano soprattutto perché riduceva proprio la materia ad estensione, la rendeva divisibile in atomi indivisibili, la rendeva passiva, la separava dal mondo del pensiero. L’estensione che ha tante proprietà (omogeneità, geometria, uniformità) non è in grado di spiegare il movimento e particolarmente la resistenza dei corpi ad esso.

        Anche Huygens non lesinò critiche e molto dure:

Il Signor Descartes aveva trovato la maniera di fare accettare per vere le sue congetture e le sue finzioni. E a coloro che leggevano i suoi Principi di Filosofia capitava qualcosa di simile a quello che capita a coloro che leggono romanzi piacevoli che diano la stessa impressione delle storie vere. La novità delle figure delle sue particelle e dei vortici piace molto. Allorché lessi questo libro dei principi per la prima volta mi sembrò che tutto andasse molto bene, e credevo, quando incontravo qualche difficoltà, che fosse colpa mia se non capivo bene il suo pensiero. Avevo soltanto 15 o 16 anni. Ma in seguito, avendovi scoperto di tanto in tanto cose visibilmente false, ed altre molto poco verosimili, abbandonai completamente le preoccupazioni che avevo nutrito, e ora non trovo quasi nulla che possa approvare per vero in tutta la sua fisica, né nella sua metafisica, né nelle sue meteore [citato da Dijksterhuis].

        Le critiche a Descartes erano particolarmente dure da parte di chi faceva scienza in un mondo che tentava di uscire faticosamente dalla metafisica, dalle magie, e dalle alchimie⁽⁴⁾. Descartes, in tali circostanze, risultava uno dei pensatori che più affidava alla metafisica le sue affermazioni sulla scienza della natura. Nonostante gli sforzi di Koyré per accreditarlo come scienziato di punta e addirittura precursore, l’immagine di Descartes è fortemente legata alla metafisica proprio perché con essa va a spiegare fatti naturali. Basti solo osservare che un gigante della matematica della sua portata costruisce la sua teoria del mondo a vortici senza che in essa intervenga minimamente la matematica medesima e tutto l’argomentare è sostenuto da ragionamenti deduttivi che lo legano pienamente alla tradizione aristotelica. La matematica vive in un comparto separato della filosofia della natura.

        Non c’è dubbio che Descartes fu il primo a sostituire un intero sistema del mondo, come realizzato da Aristotele e cristianizzato da San Tommaso, con un altro completamente differente ma anche Descartes non si sottrae a tentare l’integrazione delle novità scientifiche con la metafisica, con la religione, facendo discendere la fisica dalla metafisica:

Cosi infine non desumeremo mai nessuna ragione circa le cose naturali, dal fine che si è proposto Dio o la natura nel farle; poiché non dobbiamo essere tanto arroganti, da ritenerci partecipi delle sue decisioni: ma considerandolo come causa efficiente di tutte le cose vedremo che cosa si dovrà concludere, in base al lume naturale che egli ha posto in noi, da quei suoi attributi di cui ha voluto che avessimo qualche nozione, riguardo a quei suoi effetti che appaiono ai nostri sensi; memori tuttavia, come già s’è detto, che a questo lume naturale si deve credere sino a tanto che non venga rivelato nulla in contrario da Dio [Principia Philosophiae; 15; 87]

        È l’esistenza di Dio che rende possibile la conoscenza scientifica e ciò in quanto questa ultima è basata su dei fatti certi. E la cosa si chiude su se stessa in quanto la prova dell’immortalità dell’anima si può rintracciare proprio nella fisica. In definitiva la conclusione è che la certezza di tutti gli enunciati della conoscenza dipende dalla nostra certezza dell’esistenza di Dio. Dice Descartes:

Orbene, poiché Dio solo è la vera causa di tutte le cose che sono o possono essere, è ben chiaro che noi seguiremo la miglior via del filosofare, se tenteremo di dedurre dalla conoscenza di Dio stesso la spiegazione delle cose da lui create, in modo tale da acquistare la scienza più perfetta, che è quella degli effetti dalle cause [Principia Philosophiae; 15; 85]

ma subito dopo aggiunge che Dio appartiene alla natura dell’infinito e ci è impossibile per noi, esseri finiti, comprenderlo:

E affinché ci addentriamo qui abbastanza al sicuro e senza pericolo di errare, dovremo usare la precauzione di ricordarci sempre quanto più è possibile che Dio, autore delle cose, è infinito, e noi affatto finiti  [Principia Philosophiae; 15; 85]

        Possiamo solo affidarci alla ragione, quel lume naturale che egli ha posto in noi, per scoprire quel poco che lo stesso Dio ci permette.

        Nel fare queste considerazioni ho anticipato alcune cose dei Principia (1647), la cui prima parte è, come lo stesso Descartes afferma in una lettera a Chanut, il sunto delle Méditations métaphysiques (1641),che discuterò nella terza parte del lavoro. Mi sembrava ora necessario fare tali considerazioni anche per riportare Descartes, per la parte che riguarda i suoi lavori scientifici, ad una realistica considerazione.

NOTE

(1) Descartes a luglio del 1633 comunica all’amico Mersenne che ha terminato il suo lavoro e gli resta solo da rivedere e copiare. Subito dopo fa conoscere la sua decisione di non pubblicare il Mondo ancora a Mersenne con una lettera di fine novembre 1933 che riporto:

DESCARTES A MERSENNE [Correspondance; 2; 387]

Deventer, fine novembre 1633

[…]  mi ero proposto di inviarvi il mio Mondo per le festività di fine d’anno e non sono trascorsi neppure quindici giorni da quando ero assolutamente deciso a farvene pervenire almeno una parte se, per quel tempo, non avessi potuto ottenere che la totalità dell’opera fosse trascritta. Debbo però dirvi che – appreso che l’anno precedente era stato stampato in Italia il Sistema del Mondo [il riferimento è al Dialogo dei Massimi Sistemi, ndr] di Galileo – feci cercare in quei giorni a Leida e ad Amsterdam se non se ne trovasse una copia: mi si rispose che era vero che era stato pubblicato, ma che nello stesso tempo tutte le copie erano state date alle fiamme a Roma e il suo autore condannato a qualche pena. Il fatto mi ha tanto colpito che mi sono quasi deciso a bruciare tutte le mie carte o – almeno – a non permettere a nessuno di vederle. Non mi è parso infatti immaginabile che Galileo, italiano ed anche, come almeno mi si dice, benvoluto dal Papa, abbia potuto esser considerato un criminale per il solo fatto di avere – come avrà certamente fatto – sostenuto il moto della Terra. So bene che [tale concezione] era stata censurata da alcuni Cardinali, ma mi pareva aver anche sentito dire che da allora non si era cessato d’insegnarla pubblicamente perfino nella stessa Roma; riconosco che, se è falsa, lo sono anche tutti i fondamenti della mia Filosofia, giacché da essi tale moto si dimostra come affatto evidente. Essa è così tenuta a tutte le parti del mio Trattato che non potrei eliminarla senza rendere il resto del tutto difettoso. Non volendo però per nulla al mondo essere l’autore di un discorso ove si trovi la pur minima parola disapprovata dalla Chiesa, preferirei sopprimerlo interamente piuttosto che farlo apparire mutilato. Non sono mai stato portato a comporre libri e, se non mi fossi impegnato con promesse che ho contratte con voi e con alcuni amici per far in modo che il desiderio di mantenere la parola data mi costringesse ad applicarmi ancor più agli studi, non sarei mai venuto a capo di questo mio lavoro. Dopo tutto sono convinto che non mi invierete nessuna guardia per costringermi a pagare il debito e che forse sarete anche ben contento di esser libero della fatica di leggere povere cose. Vi sono già tante concezioni in Filosofia che possono apparire credibili ed essere sostenute nelle dispute, che se le mie non hanno qualcosa di più certo e non possono essere approvate senza controversie non vorrò mai darle alla luce. Tuttavia, visto che sarei davvero poco cortese se, dopo avervi colmato per tanto tempo di promesse, pensassi di ripagarvi con una semplice battuta, non mancherò di mostrarvi quanto ho fatto, appena mi sarà possibile: lasciate che vi chieda ancora, per favore, una proroga di un anno per aver il tempo di rivederlo e metterlo nella migliore forma possibile. Mi avete ricordato il detto oraziano: nonumque prematur in annum [tener presso di sé per nove anni, ndr], ma non sono ancora trascorsi tre anni da quando ho iniziato il Trattato che penso inviarvi; vi pregherei di farmi sapere quel che vi è noto dell’ affare di Galileo [ … ]

(2) A questo proposito Shea ricorda quanto Descartes aveva scritto tre anni prima  nelle Regulae:

Ciò che non Dice Descartes nel Mondo è che questa affermazione supponeva una rottura radicale con l’analisi delle sensazioni che egli stesso aveva offerto nelle Regulae, nelle quali sosteneva che gli oggetti fisici imprimono la loro forma nell’immaginazione e che con ciò risultava garantita l’oggettività della testimonianza dei nostri sensi.

(3) Gli altri due esempi che si trovano nei Principia (articoli 58 e 59 della Parte III) sono i seguenti:

– si fa ruotare un righello intorno ad un suo estremo e sull’altro estremo del righello si sistema una formica (vedi figura) [Principia; 15; 210]

– una pallina scende all’interno di un tubicino di vetro (vedi figura) che viene fatto girare intorno ad un suo estremo (la pallina nel tubo, mentre questo gira, si allontana dal centro di rotazione ma se il tubo si rompesse andrebbe lungo la tangente) [Principia; 15; 210-211]

(4) Altre critiche di altro segno vennero mosse a Descartes dal suo illustre concittadino Voltaire il secolo seguente nella sua famosa Lettera inglese n° 14.

        Voltaire ebbe modo di conoscere l’opera di grandi pensatori inglesi quali Bacon, Locke e Newton che saranno ispiratori dell’Illuminismo francese. Egli, pur nelle contraddizioni che lo caratterizzarono (ammirava l’Inghilterra, pur sognando non un Parlamento ma un monarca illuminato; polemizzava violentemente con la Chiesa pur credendo ad un principio divino; … ), coglie l’arretratezza del pensiero dominante del suo Paese nella filosofia di eredità scolastica di Descartes (pur difendendo il filosofo dai suoi detrattori, ad esempio, riguardo alle sue fondamentali scoperte in matematica). Gli argomenti che porta a sostegno delle aperture filosofiche di Newton rispetto alla filosofia cartesiana, sono riportati nella Lettera XIV che segue. Anche qui, ma non è il caso di sottilizzare, Voltaire non aveva capito molto bene il pensiero di Newton (anche perché. probabilmente, non lo lesse sull’opera originale ma su quella di suoi estimatori come Pemberton, Fontenelle, Maupertuis).

LETTERA XIV (Dal testo 54 di bibliografia)

Descartes e Newton

        Un francese che arrivi a Londra trova le cose assai mutate in filosofia, come in tutto il resto. Ha lasciato il mondo pieno; lo trova vuoto¹. A Parigi, si vede l’universo composto da vortici di materia sottile; a Londra, non si vede nulla di tutto questo. Da noi è la pressione della Luna che causa il flusso del mare; presso gli Inglesi è il mare che gravita verso la Luna, in modo che quando credete che la Luna dovrebbe darci l’alta marea, questi signori ritengono che si debba avere bassa marea: il che, disgraziatamente, non può controllarsi, perché sarebbe stato necessario — per chiarire la cosa — esaminare la Luna e le maree nel primo istante della creazione.

        Noterete inoltre che il Sole, il quale in Francia non c’entra per nulla in questa faccenda, vi contribuisce in Inghilterra per circa un quarto. Secondo i vostri cartesiani  tutto avviene per un impulso assolutamente incomprensibile; secondo Newton, tutto avviene per un attrazione di cui non si conosce meglio la causa. A Parigi, vi figurate la Terra fatta come un melone²; a Londra, essa è appiattita ai due poli. Per un cartesiano la luce esiste nell’aria; per un newtoniano, giunge dal Sole in sei minuti e mezzo. La chimica francese effettua tutte le sue operazioni con acidi, alcali e materia sottile; in Inghilterra, l’attrazione domina perfino nella chimica.                      

        L’essenza stessa delle cose è totalmente mutata. Non è possibile accordarvi né sulla definizione dell’anima né su quella della materia. Cartesio assicura che l’anima s’identifica col pensiero, e Locke gli prova abbastanza bene il contrario. Cartesio assicura che l’estensione da sola costituisce la materia; Newton vi aggiunge la solidità. Ecco dei contrasti abbastanza stridenti.                        

     Non nostrum inter vos tantas componere lites³. 

           Questo famoso Newton, distruttore del sistema cartesiano è morto nel mese di marzo dello scorso anno 1727. Ha vissuto onorato dai suoi compatrioti, ed è stato sepolto come un re che abbia fatto del bene ai propri sudditi  Qui a Londra è stato letto con avidità e tradotto l’elogio del signor Newton che il signor di Fontenelle⁴ ha pronunziato all’Accademia delle Scienze. In Inghilterra il giudizio del  signor di Fontenelle era  atteso  come una dichiarazione solenne della superiorità della filosofia inglese; ma quando si è visto che egli paragonava Cartesio a Newton, tutta la Società Reale di Londra si è sollevata. Lungi dall’accettare tale giudizio, si è criticato quel discorso. Parecchi (e non sono certo i più filosofi) sono anzi rimasti urtati da quel paragone, soltanto perché Cartesio era francese.

        Bisogna riconoscere che questi due grandi uomini sono stati molto diversi l’uno dall’altro per la loro condotta, la loro fortuna e la loro filosofia.

        Cartesio era nato con un’immaginazione vivace e vigorosa, che ne fece un uomo singolare nella vita privata come nella maniera di ragionare. Tale immaginazione si fa avvertire perfino nelle sue opere filosofiche, dove a ogni passo s’incontrano paragoni ingegnosi e brillanti. La natura ne aveva fatto quasi un poeta, e infatti egli compose per la regina di Svezia un divertimento in versi che, per rispetto alla sua memoria, non è stato stampato.

          Egli tentò per qualche tempo il mestiere della guerra, e poi, essendo divenuto del tutto filosofo, non credette indegno di sé il fare l’amore. Ebbe dalla sua amante una figlia di nome Francine, che morì giovane e di cui egli rimpianse molto la perdita. Così, provò tutto ciò che fa parte della natura umana.

        Credette per lungo tempo che fosse necessario fuggire gli  uomini,  e  soprattutto  la  sua  patria,  per  filosofare in libertà. Aveva ragione: gli uomini del suo tempo non ne sapevano abbastanza per illuminarlo, e non erano capaci d’altro che di nuocergli. Lasciò la Francia perché cercava la verità, che vi era perseguitata allora dalla meschina filosofia universitaria; ma non trovò un maggior raziocinio nelle università dell’Olanda, dove si ritirò. Infatti, mentre in Francia si condannavano le sole proposizioni della sua filosofia che fossero vere, egli fu perseguitato anche dai pretesi filosofi d’Olanda, che non lo capivano meglio e che, vedendo più da vicino la sua gloria, odiavano ancora di più la sua persona. Fu costretto ad abbandonare Utrecht; subì l’accusa di ateismo, estrema risorsa dei suoi calunniatori; e lui che aveva impiegato tutta la sagacia del proprio ingegno nel cercare nuove prove dell’esistenza di un Dio, fu sospettato di non riconoscerne nessuno.

    Tante persecuzioni presupponevano grandissimi meriti e una strepitosa reputazione: egli aveva infatti gli uni e l’altra. La ragione riuscì tuttavia a penetrare un po’ nel mondo attraverso le tenebre della filosofia scolastica e i pregiudizi della superstizione popolare. Il suo nome finì col diventare tanto celebre che si cercò di attirarlo in Francia mediante ricompense. Gli fu offerta una pensione di mille scudi; con tale speranza egli venne, pagò le spese del diploma, che allora si vendeva, non ebbe la pensione, e se ne ritornò a filosofare nella solitudine dell’Olanda del nord, al tempo in cui il grande Galileo, all’età di ottant’anni, gemeva nelle prigioni dell’Inquisizione, per aver dimostrato il movimento della Terra. Morì infine a Stoccolma d’una morte prematura, causata da un cattivo regime, nella cerchia di alcuni dotti, suoi nemici, e tra le mani di un medico che lo odiava.

        Completamente diversa è stata la carriera del cavaliere Newton. Ha vissuto ottantacinque anni, sempre tranquillo, felice e onorato, in patria.

        La sua grande fortuna è stata di esser nato non solo in un paese libero, ma anche in un’epoca in cui le impertinenze scolastiche erano bandite e veniva coltivata soltanto la ragione; sicché il mondo non poteva essere che suo scolaro, e non suo nemico.

        Singolare è il contrasto in cui si trova rispetto a Cartesio: nel corso della sua cosi lunga esistenza non ha avuto né passioni né debolezze; non ha mai avvicinato una donna, il che mi è stato confermato dal medico e dal chirurgo tra le cui braccia egli è morto. In questo si può ammirare Newton, ma non bisogna biasimare Cartesio.

         Su questi due filosofi, l’opinione pubblica è, in Inghilterra, che il primo era un sognatore,  e l’altro un saggio.

        A Londra pochissimi leggono Cartesio, le cui opere sono effettivamente diventate inutili; e pochissimi leggono Newton, perché per capirlo occorre essere molto dotti. Ciononostante, tutti parlano di loro: non si accorda nulla al francese, e si concede tutto all’inglese. Taluni ritengono che, se non si crede più all’orrore del vuoto, se si sa che l’aria è pesante, se ci si serve delle lenti d’ingrandimento, se ne debba esser grati a Newton. Egli è qui l’Ercole della favola, cui gli ignoranti attribuivano tutte le gesta degli altri eroi.  

        In una critica del discorso del signor di Fontenelle fatta a Londra, si è giunti a sostenere che Cartesio non era un grande matematico. Quelli che parlano così rinnegano chi li ha nutriti. Dal punto in cui ha trovato la geometria fino al punto cui l’ha portata, Cartesio ha percorso tanto cammino quanto quello percorso da Newton dopo di lui; egli è il primo che abbia trovato la maniera di dare le equazioni algebriche delle curve. La geometria, grazie a lui divenuta oggi di uso comune, era ai suoi tempi così oscura che nessun professore si azzardava a spiegarla, e non vi erano altri che Schootem⁵ in Olanda e Fermat⁶ in Francia che la capissero.

        Egli portò questo spirito geometrico e inventivo nella diottrica⁷, che divenne per opera sua un’arte del tutto nuova; e se s’ingannò in qualche cosa, è perché chi scopre nuove terre non può di colpo conoscerne tutte le caratteristiche: coloro che vengono dopo di lui e rendono fertili quelle terre hanno, nei suoi confronti, almeno l’obbligo di attribuirgli la scoperta. Non negherò invece che tutti gli altri lavori di Cartesio formicolino di errori.  

        La geometria era una guida ch’egli stesso aveva, in qualche modo, formata, e che lo avrebbe sicuramente guidato anche nel campo della fisica; tuttavia egli fini con l’abbandonare tale guida, per affidarsi allo spirito sistematico. Da allora la sua filosofia non fu più che un ingegnoso romanzo, verosimile tutt’al più per gli ignoranti. Egli si ingannò sulla natura dell’anima, sulle prove dell’esistenza di Dio, sulla materia, sulle leggi del movimento, sulla natura della luce; ammise le idee innate, inventò nuovi elementi, creò un mondo, fece l’uomo a modo suo, e si dice a ragione che l’uomo di Cartesio non è in effetti se non l’uomo di Cartesio, lontanissimo dall’uomo reale.

        Spinse i suoi errori metafisici fino a pretendere che due e due fanno quattro soltanto perché Dio ha voluto così. Ma non è troppo asserire ch’egli restava degno di stima anche nei suoi errori. Si ingannò, ma lo fece almeno con metodo e con spirito conseguente; distrusse le assurde chimere di cui la gioventù s’infatuava da duemila anni; insegnò agli uomini del suo tempo a ragionare e a servirsi contro lui stesso delle sue armi. Se non ha pagato in buona moneta, è già molto che abbia screditato quella falsa.

        Non credo, in verità, che si osi paragonare in nessun modo la sua filosofia con quella di Newton: la prima è solo un tentativo, la seconda un capolavoro. Ma chi ci ha messi sulla via della verità vale forse quanto colui che è salito poi sulla vetta di tale carriera.

        Cartesio diede la vista ai ciechi: essi videro gli errori dell’antichità ed i suoi. La via ch’egli ha aperto è, dopo di lui, divenuta immensa. Il libretto di Rohault⁸ ha rappresentato per qualche tempo una fisica completa; oggi, tutte le raccolte delle Accademie d’Europa non costituiscono nemmeno un inizio di sistema: approfondendo quell’abisso, lo si è trovato infinito. Si tratta adesso di vedere che cosa il signor Newton ha cavato fuori da tale abisso.

____________________________

NOTE ALLA LETTERA XIV

1 – Allusione, rispettivamente, alle posizioni filosofiche di Cartesio e di Newton. R. Naves osserva: «Tutto l’inizio di questa lettera è scritto in tono scherzoso, e Voltaire fa mostra di non decidere tra Descartes e Newton. …  La fine della lettera XIV prende partito a favore di Newton e giudica  Descartes  negli stessi termini che Voltaire riprenderà molto più tardi. Poteva essere abile non spaventare il  lettore  fin  dall’inizio  e  condurlo  soltanto  gradualmente  alla  “sana filosofia”».

2 –  La  tesi  che  la  Terra  fosse  uno  sferoide  allungato  anziché  appiattito ai due Poli era stata sostenuta dall’astronomo francese di origine   italiana  Jacques Cassini (1677-1756), direttore dell’osservatorio di Parigi, nell’opera La grandeur et la figure de la Terre (1718) e accolta da altri scienziati.

3 – “Non è affar nostro appianar tra voi dispute così importanti“; VIRGILIO, Bucoliche, III, 108. …

4 – Bernard Le Bovier de Fontenelle (1657-1757), letterato francese, Segretario perpetuo dell’Accademia delle Scienze: in tale qualità compose numerosi elogi di colleghi defunti, tra cui quello di Newton che ebbe nel 1728 ben quattro edizioni.

5 – Francesco von Schooten, matematico olandese del XVII secolo, autore di una Geometria dedicata a Descartes (Leida 1649) in cui sono stabilite le coordinate ottagonali, e di un’altra opera del 1656 dedicata alla « geometria con la riga ».

6 – Pierre  Fermat  (1601-65),  matematico  francese  in  relazione  con Cartesio, sviluppò la geometria analitica deducendo dall’equazione di una curva (da lui chiamata « Proprietà specifica ») tutte le sue proprietà>

7 – Parte della fisica che si occupa dell’azione dei mezzi sulla luce che li attraversa. 8 – Jacques Rohault (1620-1675), autore di un Traité de physique (1671) assai diffuso, in cui sono esposte le dottrine di Cartesio.  

BIBLIOGRAFIA

 1 – René Descartes – Opere scientifiche (a cura di Gianni Micheli) – UTET 1966

 2 – René Descartes – Opere filosofiche (a cura di Ettore Lojacono) – UTET 1994

 3 – A. Massarenti (a cura di), P. Pettinotti – Cartesio: vita, pensiero, opere scelte – Il Sole 24 ore 2006 

 4 – S. Gaukroger – Descartes, an intellectual biography – Clarendon Press 1995

 5 – G. Rodis-Lewis – Cartesio. Una biografia – Editori Riuniti 1997

 6 – William R. Shea – The Magic of Numbers & Motion: The Scientific Career of René Descartes – Watson Publishing International 1991

 7 – Pierre Mesnard – Cartesio – Accademia 1972

 8 – Giambattista Gori (a cura di) – Cartesio – ISEDI 1977

 9 – Giovanni Crapulli (a cura di) – Il pensiero di René Descartes – Loescher 1970

10 – Desmond M. Clarke – Descarte’s Philosophy of Science – Manchester University Press 1982

11 – Guido De Ruggiero – L’età cartesiana – Laterza 1972

12 – René Descartes – Discours de la méthode – Flammarion 1966

13 – René Descartes – Méditations métaphysiques – Flammarion 1979

14 – René Descartes – Il mondo. L’uomo – Laterza 1969

15 – René Descartes – I principi della filosofia – Bollati Boringhieri 1992

16 – Alexander Koyré – Studi galileiani – Einaudi 1979

17 – Alexander Koyré – Studi newtoniani – Einaudi 1972

18 – Bertrand Russel – Storia della filosofia occidentale – Longanesi 1967

19 – Harald Höffding – Storia della filosofia moderna – Sansoni 1978

20 – Nicola Abbagnano – Storia della filosofia – UTET 1993

21 – Jaime Labastida – Producción, ciencia y sociedad: de Descartes a Marx – Siglo veintiuno 1972

22 – L. Figuer – La ciencia y sus hombres – D. Jaime Seix Editor 1880

23 – U. Forti – Storia della scienza – Dall’Oglio 1968

24 – L. Geymonat (diretta da) – Storia del pensiero filosofico e scientifico – Garzanti 1970

25 – R. Tatón (coordinata da) – Storia generale delle scienze – Casini 1964

26 – Hugh Kearney – Science and Change 1500 – 1700 – Weidenfeld and Nicolson. 1971

27 – H. Butterfield – Le origini della scienza moderna – il Mulino 1962

28 – Richard S. Westfall – La rivoluzione scientifica del XVII secolo – il Mulino 1984

29 – Paolo Rossi – La nascita della scienza moderna in Europa – Laterza 2000

30 – Maurizio Mamiani – Storia della scienza moderna – Laterza 2002

31 – Eric T. Bell – I grandi matematici – Sansoni 1966

32 – Hugo Dingler – Storia filosofica della scienza – Longanesi 1949

33 – Paolo Rossi (diretta da) – Storia della scienza – UTET 1988

34 – Robert Lenoble – Le origini del pensiero scientifico moderno – Laterza 1976

35 – A. Rupert Hall – Da Galileo a Newton – Feltrinelli 1973

36 – E.J. Dijksterrhuis – Il meccanicismo e l’immagine del mondo – Feltrinelli 1971

37 – Carl B. Boyer – Storia della matematica – Mondadori 1980

38 – Morris Kline – Matematical thought from ancient to modern times – Oxford University Press, 1972

39 – Maurice Daumas (a cura di) – Storia della scienza – Laterza 1976

40 – Nicola Abbagnano (coordinata da) – Storia delle scienze – UTET 1965

41 – I. Bernard Cohen – La rivoluzione della scienza – Longanesi 1988

42 – A. C. Crombie – Cartesio in Fisica e Cosmo (articolo pubblicato da Scientific American ottobre 1959) – Zanichelli 1969

43 – Descartes – Oeuvres choisies – Librairie Garnier, Paris [data ?]

44 – Descartes – The Geometry – in Descartes, Spinoza – Encyclopaedia Britannica 1952

45 – A.R. Hall e M. Boas Hall – Storia della scienza – il Mulino 1979

46 – Charles Singer – Breve storia del pensiero scientifico – Einaudi 1961

47 – Vasco Ronchi – Storia della luce – Zanichelli 1939

48 – S. Sambursky – The Physical World of Late Antiquity – Routledge & Kegan 1962.

49 – Eugenio Garin – Vita ed opere di Cartesio – Laterza 1984

50 – Salvo D’Agostino – Dispense di Storia della Fisica (a.a. 1972/73) – IFUR 1972.

51 – Roberto Pitoni – Storia della fisica – S.T.E.N. 1913.

52 – Mary B. Hesse – Forze e campi – Feltrinelli 1974.

53 – David Park – Natura e significato della luce – McGraw-Hill 1998.

54 – François-Marie Arouet (Voltaire) – Lettere inglesi – Editori Riuniti 1971

16 ore fa

Categorie:Senza categoria