Ingegneria Meccanica – Roma Tre
AA/2011-2012
APPUNTI PER IL CORSO
(Ripresi e sistemati, con differente organizzazione e varie integrazioni, dai testi di bibliografia)
Roberto Renzetti
PARTE QUARTA

DINAMICA DEL CORPO RIGIDO

Bibliografia: Paul J. Tipler, Gene Mosca – Corso di Fisica – Zanichelli, UARTA
Jay Orear – Fundamental Physics – John Wiley & Sons Inc, 1967
F.W. Sears, M.W. Zemansky – University Physics – Addison-Wesley Publishing Company, 1964
M. Alonso, E.J. Finn – Fundamental University Physics – Addison-Wesley Publishing Company, 1969
R. Renzetti – Vari appunti miei raccolti negli anni – http://www.fisicamente.net

DINAMICA DEL CORPO RIGIDO

1 – Velocità angolare ed accelerazione angolare

Se consideriamo una sega circolare e calcoliamo la sua energia cinetica riferendola al baricentro, troviamo EC = ½ m.0 = 0 (perché la velocità del baricentro è in questo caso nulla). Dovremo allora considerare questo oggetto ruotante come un sistema di punti materiali, ciascuno con una sua velocità differente dall’altra. L’energia cinetica di questo corpo rigido ruotante sarà la somma delle energie cinetiche di tutte le particelle che costituiscono il corpo.  Ma un conto del genere è complesso proprio perché le velocità delle singole particelle sono tutte differenti. Nel seguito vedremo come risolvere il problema.

Un corpo rigido è definito come un corpo che, comunque si muova, mantiene inalterata la distanza tra due particelle che lo compongono. Un tale corpo si può muovere o secondo una traslazione del suo centro di massa o secondo una rotazione del corpo intorno ad un asse passante per il centro di massa o secondo ambedue i moti ora detti. Riguardo al moto rotatorio, esso è in generale complesso perché, nel ruotare, l’asse di rotazione del corpo cambia orientamento. Noi ci limiteremo in questo capitolo allo studio della rotazione di un corpo rigido intorno ad un asse fisso.
Consideriamo una particella di una ruota che gira intorno al suo asse di simmetria, fisso nello spazio. Si può specificare la posizione della particella Pi mediante la distanza ri dal centro della ruota e l’angolo θ fra una retta condotta dal centro alla particella e una retta di riferimento nello spazio, com'è indicato nella figura. 

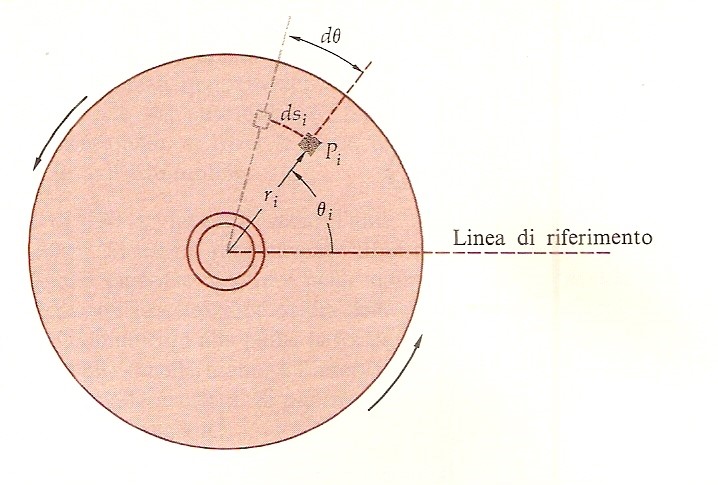
In un tempo dt, la particella si sposta lungo un arco di circonferenza percorrendo la distanza dsi data da:

(1) ds_i = v_idt

dove vi è la velocità della particella. L’angolo descritto dalla congiungente il centro e la particella, espresso in radianti, è uguale al rapporto fra la distanza e il raggio ri:

Dall’equazione (2) risulta che la velocità della particella i-esima è legata al suo raggio ri e alla velocità angolare della ruota dalla relazione:

Il fatto che ω sia positiva o negativa dipende dal fatto che θ cresca o decresca. L’unità di velocità angolare nel sistema SI è il radiante al secondo (rad/s). Poiché un radiante è un’unità di angolo adimensionata, le dimensioni della velocità angolare sono quelle di un tempo alla meno uno [s – l]. Sebbene la velocità angolare sia spesso espressa in unità diverse dal radiante al secondo, è importante ricordare che espressioni quali le equazioni (3) e (4) e gli altri risultati che otteniamo per il moto rotatorio sono validi solo quando gli angoli sono espressi in radianti (si ricordi comunque che 2π rad = 3600). La velocità angolare è espressa comunemente in giri al secondo e in giri al minuto. La conversione in radianti si esegue mediante la relazione 2π rad = l giro.

La rapidità di variazione della velocità angolare rispetto al tempo e chiamata accelerazione angolare α. Per la rotazione intorno a un asse fisso:

Perciò:

Le tre grandezze spostamento angolare θ, velocità angolare ω e accelerazione angolare α sono analoghe allo spostamento lineare x, alla velocità lineare vx e all’accelerazione lineare ax, che abbiamo incontrato nello studio del moto unidimensionale. In virtù dell’analogia fra le definizioni delle grandezze rotazionali e lineari, gran parte di ciò che si è appreso in precedenza potrà essere usato per affrontare i problemi della rotazione intorno a un asse fisso.

Per esempio, se l’accelerazione angolare è costante, si possono sviluppare espressioni per l’accelerazione angolare costante che hanno la stessa forma delle espressioni per l’accelerazione lineare costante. Se, per esempio, si ha:

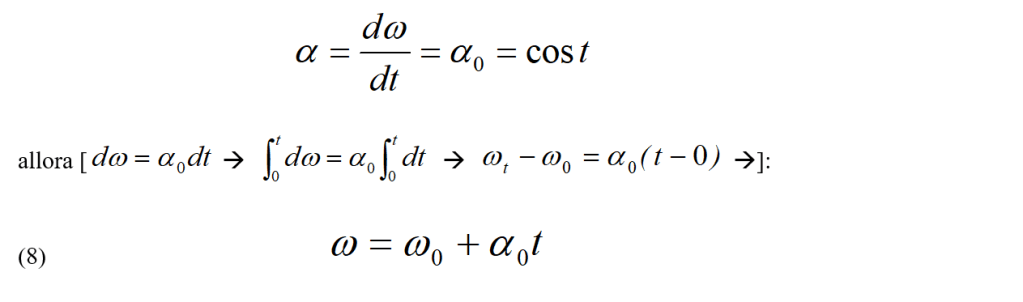
dove ω₀ è la velocità angolare nell’istante t = 0.
Ricordando la (3) si può integrare di nuovo, ottenendo successivamente:

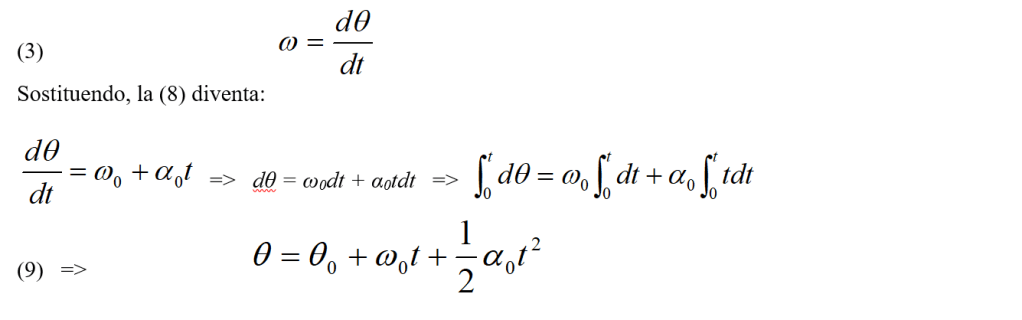
Come nel caso delle formule per l’accelerazione lineare costante, si può eliminare il tempo da queste equazioni per ottenere un’equazione che leghi lo spostamento angolare, la velocità angolare e l’accelerazione angolare (dalla 8 si ricava il tempo t che si sostituisce nella 9; da qui, risolvendo con banale algebra, si trova):

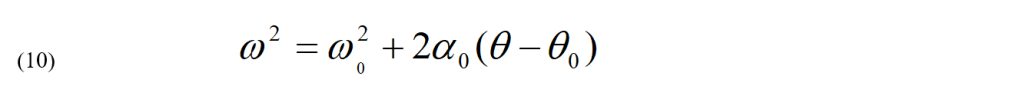
Conviene assegnare un’orientazione alle grandezze rotazionali θ, ω ed α. Non si può descrivere la rotazione di una ruota per mezzo di qualunque direzione nel piano della ruota perché, per ragioni di simmetria, tutte le direzioni in questo piano si equivalgono. La direzione nello spazio associata univocamente alla rotazione è la direzione dell’asse di rotazione. Perciò, scegliamo lungo l’asse di rotazione la direzione per l’angolo di rotazione. Poiché ω è uguale alla rapidità di variazione di θ, anche essa è orientata lungo l’asse di rotazione. In modo analogo, poiché si considerano solo rotazioni intorno ad assi fissi nello spazio, la rapidità di variazione di ω, che è l’accelerazione angolare α, deve essere orientata anch’essa in questa direzione.

Si consideri ora una ruota che gira in senso orario, come nella figura.

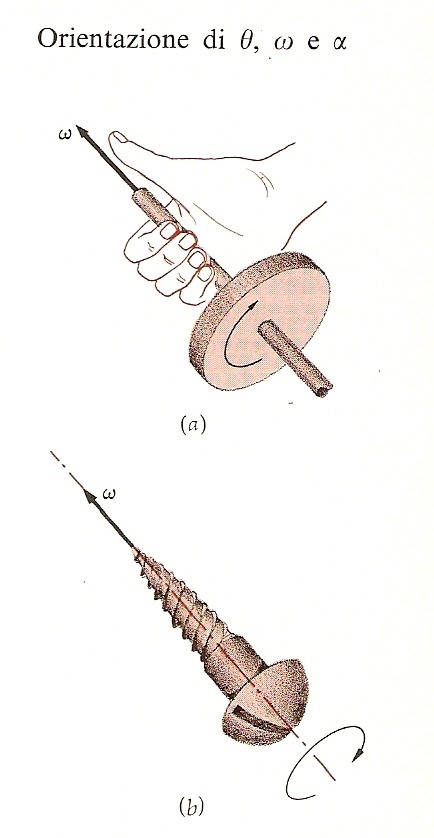
Abbiamo scelto la direzione per ω lungo l’asse di rotazione, ma dobbiamo ancora decidere il verso di ω, cioè, per questa rotazione, se ω entra nel piano del foglio o esce dal piano del foglio. La scelta è convenzionale. Se la rotazione è oraria, come nella figura, ω è rivolta verso l’interno; se è antioraria, ω è rivolta verso l’esterno. Questa decisione arbitraria è chiamata regola della mano destra, com’è illustrato nella figura (a). Quando l’asse di rotazione è afferrato con la mano destra con le dita piegate nel verso della rotazione, il pollice disteso è orientato nella direzione e nel verso di ω. La direzione e il verso di ω sono anche quelli in cui avanza una vite destrorsa nella sua rotazione, com’è illustrato nella figura (b). Il verso dell’accelerazione angolare (per la rotazione intorno a un asse fisso) dipende dal fatto che ω sia crescente o decrescente. Se ω è crescente, α è concorde con ω; se ω è decrescente, α è discorde con ω.

NATURA VETTORIALE DELLA ROTAZIONE (argomento già visto)

Avendo assegnato un’orientazione, cioè una direzione e un verso, alle grandezze rotazionali θ, ω ed α, possiamo ora chiederci se queste grandezze sono vettori. Una grandezza che ha un valore numerico, una direzione e un verso è un vettore solo se ubbidisce anche alla regola di composizione dei vettori. La proprietà della regola di composizione dei vettori che è importante per questa discussione è il fatto che la somma di due vettori è indipendente dall’ordine in cui vengono sommati (proprietà commutativa):

                                       A + B = B + A

Per una rotazione generica, la velocità angolare è definita da:

Poiché la derivata di un vettore è anch’essa un vettore, è un vettore.

Per le rotazioni intorno a un asse fisso, il carattere vettoriale delle grandezze rotazionali non è importante. La velocità angolare ω e l’accelerazione angolare α hanno soltanto una componente, quali ωz e αz per una ruota che gira intorno all’asse z. Perciò, possono variare soltanto in modulo. Stiamo considerando una semplificazione del moto rotatorio generale, la quale è analoga alla semplificazione del moto lineare quando abbiamo limitato la discussione al moto unidimensionale.

2 – Energia cinetica di rotazione e momento d’inerzia

L’energia cinetica di un sistema di particelle è semplicemente la somma delle energie cinetiche delle singole particelle. Per una ruota in rotazione, si ha:

Confrontando questa espressione con quella per l’energia cinetica di traslazione di una singola particella, ½ mv2, si vede che nel moto rotatorio il momento d’inerzia è analogo alla massa nel moto lineare, così come la velocità angolare è analoga alla velocità lineare. Si rilevi che nell’equazione (11) la distanza ri è la distanza fra la particella i-esima e l’asse di rotazione. In generale non è la distanza fra la particella i-esima e il centro di massa anche se in una figura bidimensionale rotante intorno a un asse perpendicolare alla figura e passante per il centro di massa le due distanze coincidono.
Per evitare di confondere ri con il suo significato usuale (distanza della particella i-esima dall’origine) useremo il simbolo ρi per designare la distanza della particella i-esima dall’asse di rotazione (mentre ri rappresenterà la distanza della particella i-esima dall’origine). Quindi, il momento d’inerzia è:

CALCOLO DEL MOMENTO D’INERZIA

Si può spesso semplificare il calcolo dei momenti d’inerzia per vari corpi usando teoremi generali che mettono in relazione il momento d’inerzia rispetto a un asse del corpo con quello rispetto a un altro asse. Il teorema di Huygens-Steiner, o teorema del trasporto, stabilisce una relazione fra il momento d’inerzia rispetto a un asse passante per il centro di massa e quello rispetto a un secondo asse parallelo al primo. Sia ICM il momento d’inerzia rispetto a un asse passante per il centro di massa di un corpo e sia I il momento d’inerzia rispetto a un asse parallelo situato a una distanza h dal primo. Il teorema di Huygens-Steiner stabilisce che:

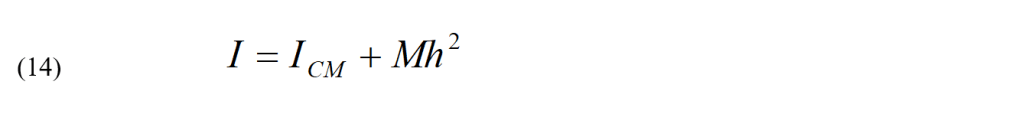
dove M è la massa totale del corpo (vedi figura).

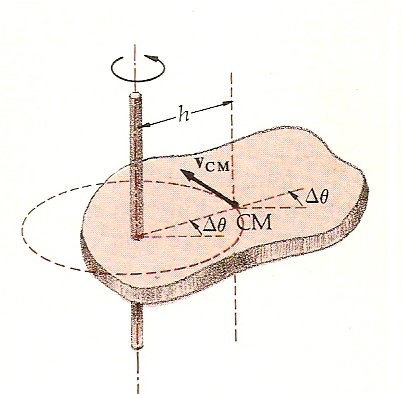
Nel caso di una figura piana (sistema piano) si può dimostrare che esiste una relazione fra i momenti d’inerzia rispetto a due assi perpendicolari fra loro e giacenti sulla figura e il momento d’inerzia rispetto a un terzo asse perpendicolare alla figura. Se x, y e z sono assi perpendicolari per una figura che giace nel piano xy, il momento d’inerzia rispetto all’asse z è uguale alla somma dei momenti d’inerzia rispetto agli assi x e y. Questa asserzione non è difficile da dimostrare. La figura seguente rappresenta una figura piana nel piano xy.

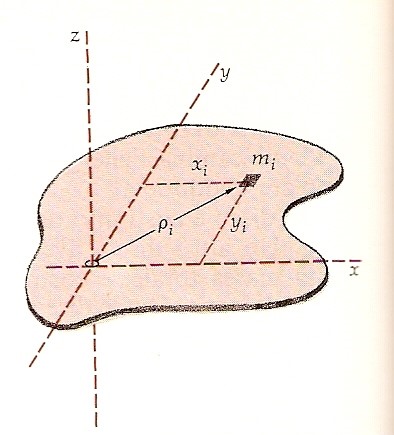
Il momento d’inerzia rispetto all’asse x è:

Ma per ciascun elemento mi, ρi2 = xi2 + yi2. Perciò:

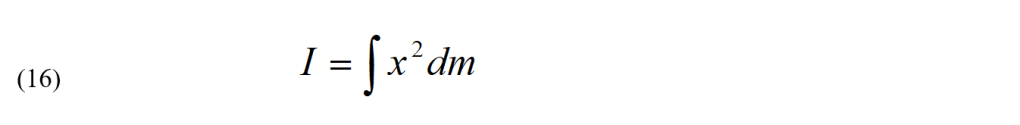
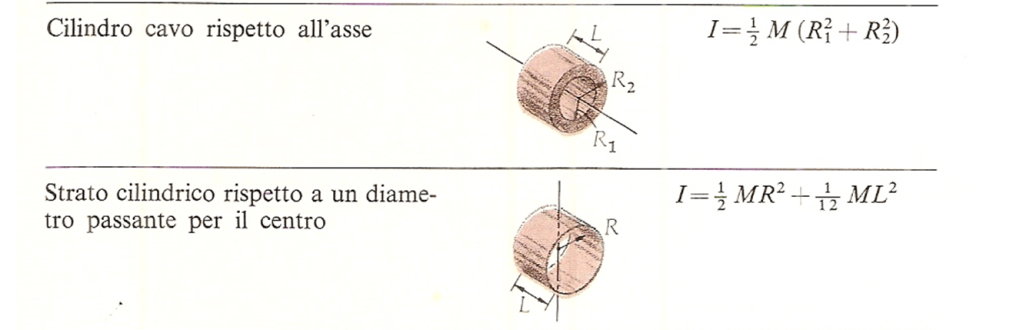
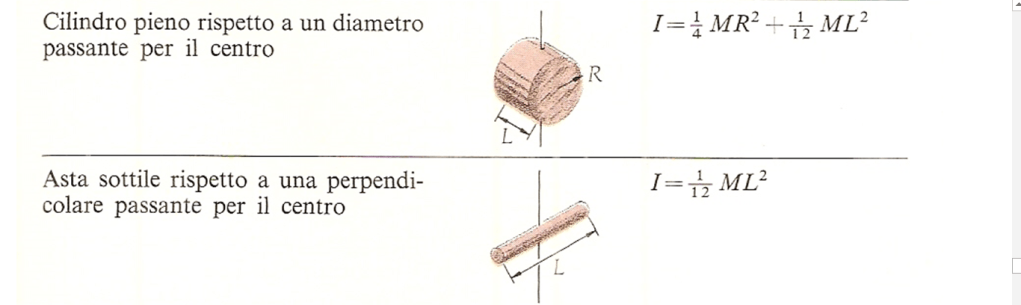
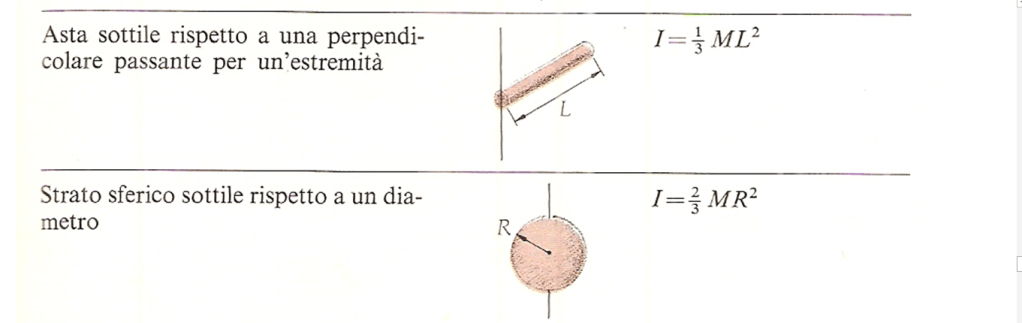
Di seguito riporto i momenti d’inerzia di corpi uniformi di varie forme.

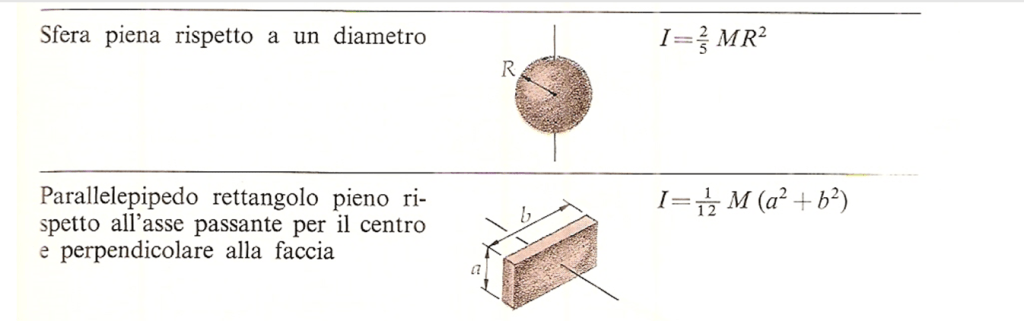
3 – Momento di una forza

Consideriamo ora la dinamica della rotazione di un corpo rigido. Perché vari l'energia cinetica di rotazione di un corpo rigido, una forza deve eseguire un lavoro sul corpo. Si considerino le forze Fl ed F2 agenti sul bordo di una ruota, com'è indicato nella figura. 

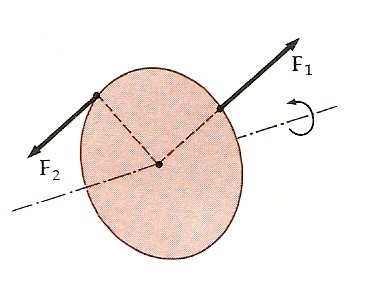
La forza F1 è diretta lungo un raggio della ruota ed è perpendicolare al moto del punto sul bordo della ruota in cui agisce la forza. Perciò non esegue lavoro sulla ruota e non può influenzare la sua energia cinetica. Poiché l’energia cinetica è ½ Iω2, questa forza non può influenzare la velocità angolare della ruota. Per esempio, se la ruota non gira affatto, una forza radiale Fl non produrrà rotazione né in un verso né nell’altro. Ma la forza F2 ha una componente concorde o discorde con il moto del bordo della ruota (secondo il verso in cui gira la ruota quando è applicata la forza). Questa forza esegue sulla ruota un lavoro che varia la sua energia cinetica. Per esempio, se la ruota gira in senso antiorario come in figura (con la regola della mano destra, ω orientata verso l’esterno), la componente tangenziale di F2 avrà la stessa orientazione del moto del bordo e la forza eseguirà un lavoro positivo, aumentando l’energia cinetica e perciò aumentando il modulo della velocità angolare. Se la ruota gira nel senso opposto, F2 eseguirà un lavoro negativo, diminuendo ω e l’energia cinetica.

Naturalmente, le forze Fl ed F2 rappresentate nella figura precedente non sono le uniche forze agenti sulla ruota. Se la ruota gira intorno a un asse fisso passante per il centro di massa, questo deve essere in quiete. Allora la forza risultante agente sulla ruota dev’essere nulla. Le altre forze non rappresentate in questa figura sono esercitate dal perno in corrispondenza dell’asse di rotazione ed equilibrano F1 ed F2 in modo che il centro di massa non acceleri. Se il perno è privo d’attrito, le forze sono radiali e non influenzano la rotazione. Trascureremo queste forze per la presente discussione. Consideriamo ora una singola forza F agente su una ruota che già gira nel senso antiorario (ω verso l’esterno), come nella figura seguente.

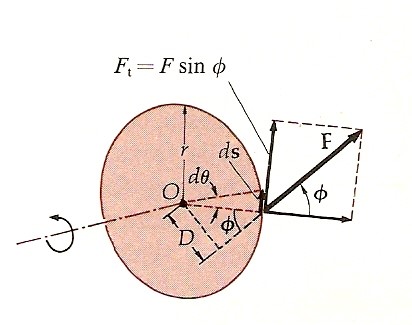
La forza forma un angolo φ con la linea radiale condotta dall’asse di rotazione al punto di applicazione della forza. La componente tangenziale della forza è Ft = F sin φ. (usiamo φ per evitare che questo angolo sia confuso con l’angolo di rotazione θ). In un tempo dt, la ruota gira di un angolo dθ = ω dt. Il punto di applicazione della forza percorre una distanza ds = r dθ = rω dt. Il lavoro compiuto dalla forza è perciò:

Eliminando ω nell’equazione (2), si ottiene:

Abbiamo quindi che il momento di una forza è uguale al prodotto della forza per il braccio della forza che è la distanza b = r sin φ. Questo momento è diretto perpendicolarmente al piano formato da F ed r. Possiamo vedere in una figura più semplice il risultato trovato:

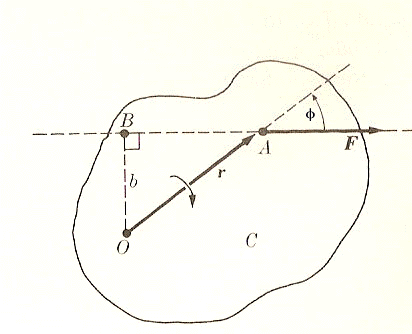
Il momento M è, come già detto, una grandezza vettoriale data dal prodotto

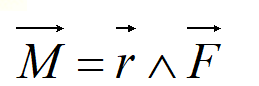
. Tenendo presenti le proprietà del prodotto vettoriale, il momento è rappresentato da un vettore perpendicolare sia ad r che ad F; vale a dire, perpendicolare al piano passante per r e per F, e diretto come il senso di avanzamento di una vite destrorsa che ruota nel medesimo senso della rotazione prodotta da F intorno ad O. Ciò è indicato nella figura seguente.

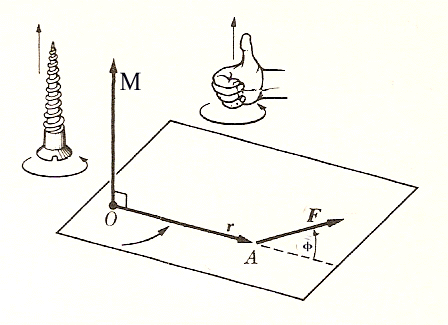
C’è da sottolineare il ruolo del braccio b. L’esperienza quotidiana ci suggerisce che l’efficacia di F per quanto riguarda la rotazione del corpo aumenta con l’aumentare della distanza b = OB fra il punto O e la retta di azione della forza. Per esempio, quando apriamo una porta, noi tiriamo o spingiamo sempre il più lontano possibile dai cardini, e tentiamo di mantenere la direzione di spinta o di tiro perpendicolare alla porta. Questa esperienza suggerisce pertanto la convenienza di definire la quantità fisica momento della forza, mediante la relazione forza x braccio. Di conseguenza, il momento deve essere espresso dimensionalmente come il prodotto dell’unità di forza per l’unità di distanza. Vogliamo sottolineare che il momento di una forza è definito rispetto a un punto dello spazio (e non rispetto a un asse, come il momento d’inerzia di un corpo). Nel sistema SI il momento è espresso in N.m.

Anche in questo caso conviene assegnare una direzione e un verso al momento della forza. Abbiamo scelto un caso in cui il momento della forza aumenta il valore di ω e vogliamo che in questo caso la direzione e il verso del momento della forza siano uguali alla direzione e al verso di ω. Per definizione, la direzione e il verso del momento della forza è la direzione e il verso della velocità angolare ω che il momento della forza, agendo da solo, produce se il corpo parte dalla quiete. L’equazione 6 può essere scritta sotto forma di equazione vettoriale. Se più forze esercitano momenti sulla ruota, è il lavoro eseguito dal momento risultante che è uguale alla variazione dell’energia cinetica. Perciò, sostituendo ΣM ad M, nelle equazioni precedenti, si ottiene:

4 – Momento angolare (o momento della quantità di moto) e sua conservazione

Sia ora il punto A delle ultime due figure un punto in moto rispetto ad un dato riferimento e p = mv la sua quantità di moto. Per definizione, il momento angolare o momento della quantità di moto q di una particella rispetto all'origine O è il prodotto vettoriale del vettore posizione r per la quantità di moto p (si veda la figura) 

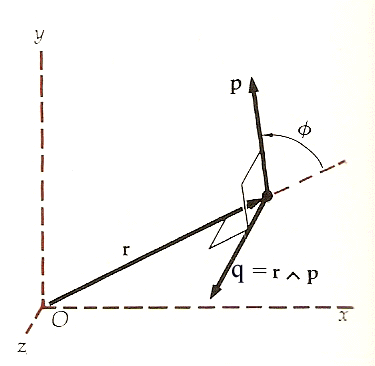
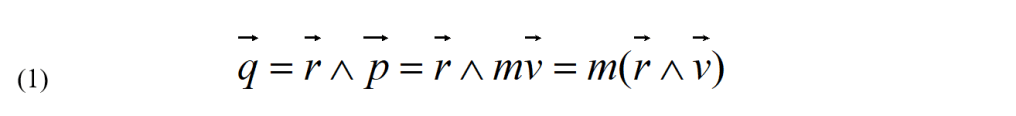
Come il momento di una forza, il momento angolare è definito rispetto a un punto dello spazio. Il suo modulo è il prodotto del modulo della quantità di moto, p, per r sin φ, che è la distanza dell’origine dalla direzione del moto. Oppure, q è il prodotto della distanza r per p sin φ, che è la componente della quantità di moto perpendicolare a r.

Supponiamo ora che A si muova sotto l’azione di una forza f. Calcoliamoci il momento della quantità di moto di A rispetto ad O. Dalla seconda legge di Newton, sappiamo che:

nulla:

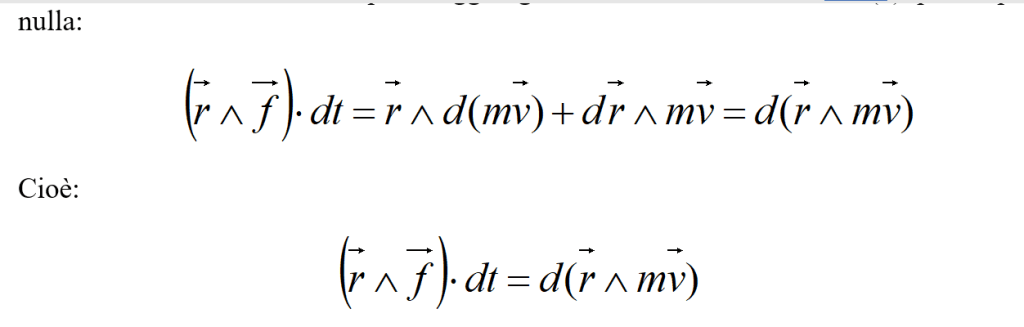
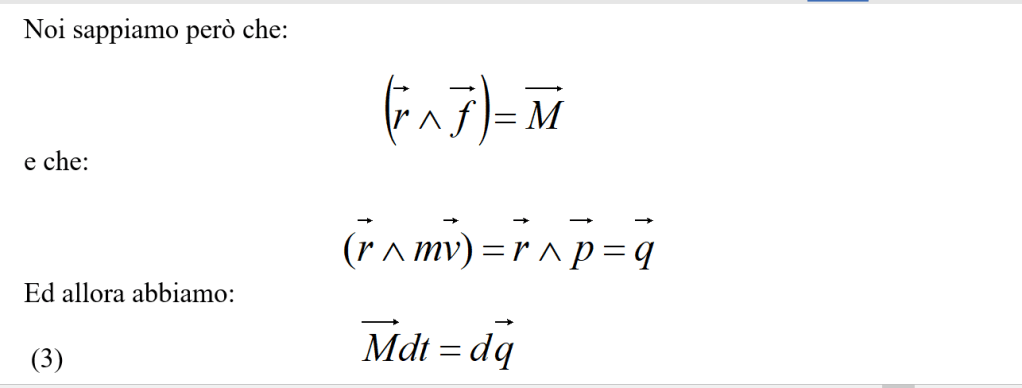
Alla quantità M.dt si dà il nome di momento dell’impulso della forza applicata ad un punto materiale: esso risulta uguale a dq, cioè alla variazione del momento della quantità di moto del medesimo punto materiale.

Nel ricavare la (3) siamo arrivati a stabilire una equazione di grande importanza. Essa insieme ad un’altra equazione che già conosciamo, costituiscono le equazioni cardinali della meccanica:

I singoli momenti angolari  qi variano nel tempo e tale variazione è data da:

.

:
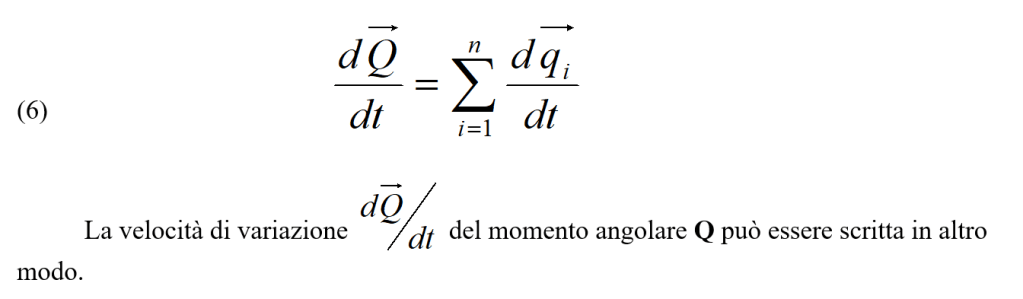
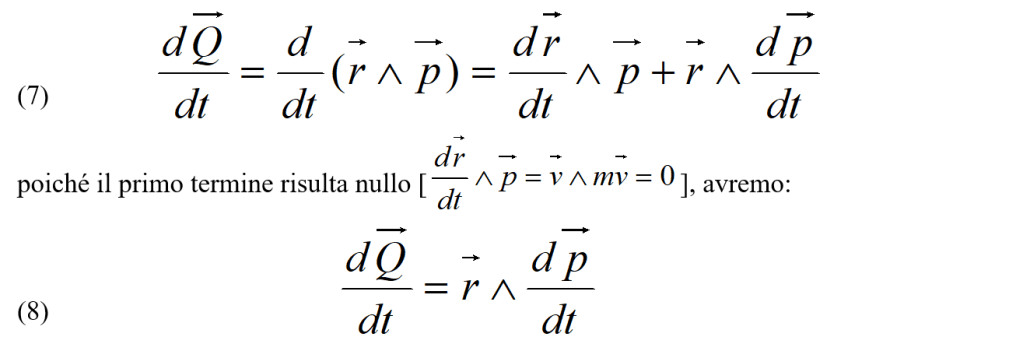
cioè:

Si osservi che se il momento delle forze esterne agenti sul sistema è nullo, risulta:

Abbiamo quindi visto che se il momento risultante delle forze esterne che agiscono su un sistema è nullo, il momento angolare totale è costante. Si ha così un terzo principio di conservazione per i sistemi isolati. L’energia, la quantità di moto e il momento angolare si conservano. Il principio di conservazione del momento angolare è una fondamentale legge naturale. Anche sulla scala microscopica della fisica atomica e nucleare, in cui la meccanica newtoniana non è valida, il momento angolare di un sistema isolato è costante nel tempo. Un paio di esempi grafici possono ulteriormente aiutare a comprendere cosa vuol dire conservazione del momento angolare

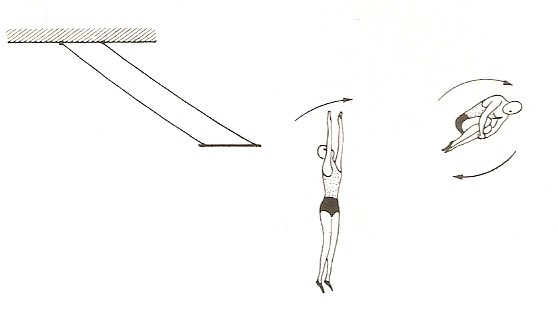
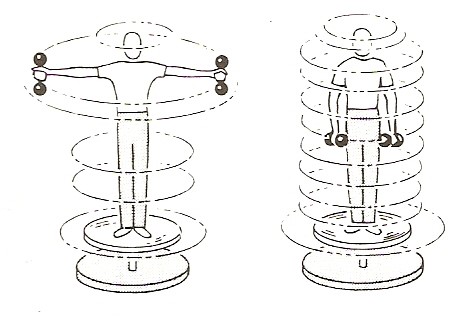
Vediamo ora un esempio di conservazione del momento angolare.

5 – Il pendolo composto

Riscrivo qui cose scritte quando abbiamo trattato il momento di una forza ed il momento angolare.

Il momento di una forza è uguale al prodotto della forza per il braccio della forza che è la distanza b = r sin φ. Questo momento è diretto perpendicolarmente al piano formato da F ed r.

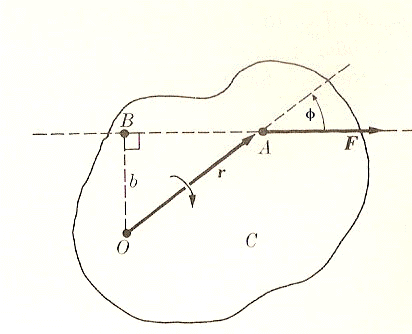
Il momento M è una grandezza vettoriale data dal prodotto

Tenendo presenti le proprietà del prodotto vettoriale, il momento è rappresentato da un vettore perpendicolare sia ad r che ad F; vale a dire, perpendicolare al piano passante per r e per F, e diretto come il senso di avanzamento di una vite destrorsa che ruota nel medesimo senso della rotazione prodotta da F intorno ad O. Ciò è indicato nella figura seguente (già vista e che riporto per comodità).

Riporto di nuovo ed ancora per comodità, una definizione già data. Il momento angolare o momento della quantità di moto q di una particella rispetto all'origine O è il prodotto vettoriale del vettore posizione r per la quantità di moto p 

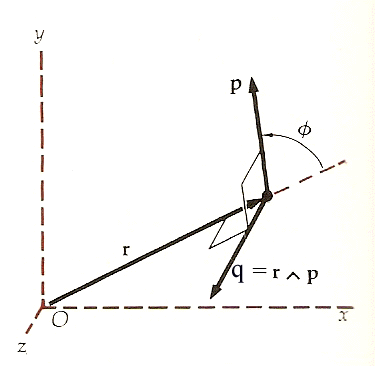
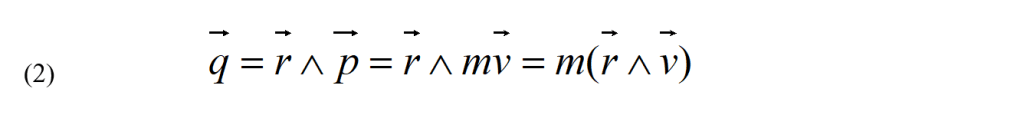
Come il momento di una forza, il momento angolare è definito rispetto a un punto dello spazio. Il suo modulo è il prodotto del modulo della quantità di moto, p, per r sin φ, che è la distanza dell’origine dalla direzione del moto. Oppure, q è il prodotto della distanza r per p sin φ, che è la componente della quantità di moto perpendicolare a r.

Ricordati questi concetti, dimostriamo che la seconda legge della dinamica implica che la velocità di variazione del momento angolare è uguale al momento della forza.
La seconda legge, per un sistema di particelle in moto lineare, è:

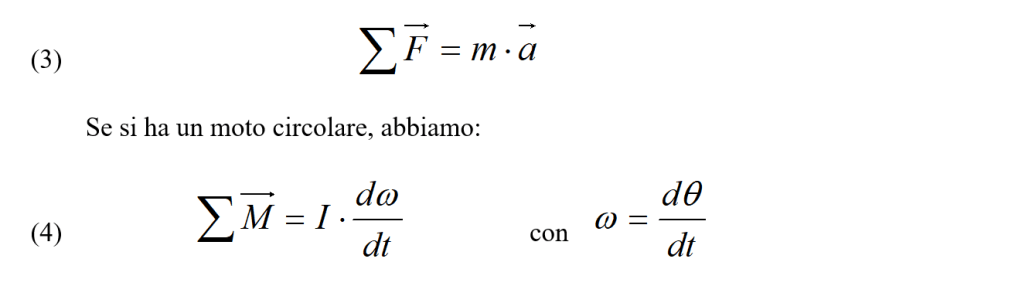
dove dω/dt  è l’accelerazione angolare ed I è il momento d’inerzia. La (4) si può anche scrivere nel modo già visto:

Il momento Σ M della forza vale in questo caso:

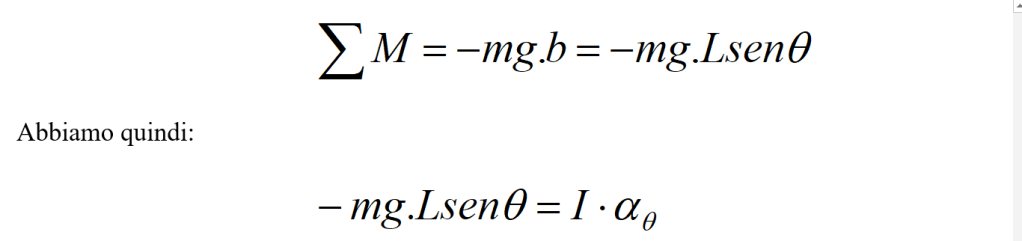
[avendo indicato con aθ l’accelerazione alla quale è soggetto l’angolo θ].
Si dimostra che è possibile ricavare I attraverso il raggio d’inerzia o di girazione che è L e la massa totale del corpo che è m [I = mL2] ed abbiamo quindi:

da cui:

:

Quindi il pendolo composto si muove di moto armonico semplice e, sempre nell’ipotesi sen θ ≈ θ, si ha:

con

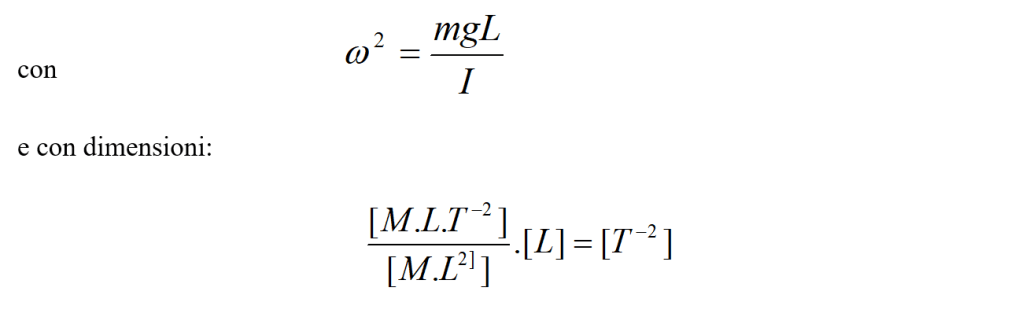
Il periodo sarà:

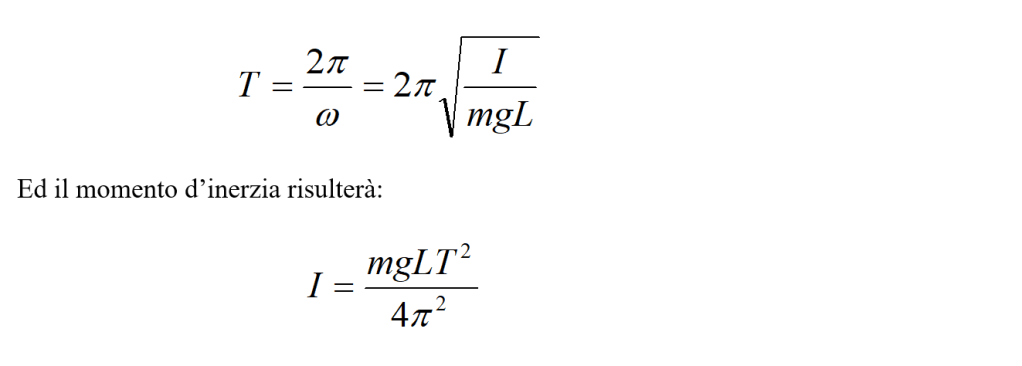
:6 – Condizioni di equilibrio statico di un corpo rigido

Se un corpo resta in quiete si dice che è in equilibrio statico. Un problema importante è determinare le forze che agiscono sul corpo quando è in equilibrio statico. Abbiamo già trovato che una condizione necessaria perché una particella sia in quiete è che la forza risultante sia nulla. Allora la particella non accelera e la sua velocità, se è inizialmente nulla, rimane tale. Poiché l'accelerazione del centro di massa di un corpo è uguale al rapporto fra la forza risultante e la massa totale, questa condizione è necessaria anche perché un corpo rigido sia in equilibrio. Però, anche se il centro di massa del corpo è in quiete, il corpo può ruotare. Perciò, è anche necessario che il momento della forza, risultante rispetto al centro di massa sia nullo. Se il centro di massa di un corpo è in quiete e il corpo non ruota intorno a esso, non ruota neppure intorno ad alcun altro punto. 

Le condizioni per l’equilibrio statico di un corpo rigido sono perciò:

1- La risultante delle forze esterne deve essere nulla: ΣF = 0

2 – Il momento della forza risultante dei momenti delle forze esterne (o, più semplicemente, il momento delle forze esterne) rispetto a qualunque punto dev’essere nullo: ΣM = 0

Nel fornire esempi dell’applicazione di queste condizioni vorremo spesso sostituire due o più forze agenti su un corpo con un’unica forza equivalente. Quando due forze F1 ed F2 agiscono su un’asta come nella figura seguente, l’unica forza che ha lo stesso effetto sulla traslazione del centro di massa del corpo è la somma Σ F = F1 + F2.

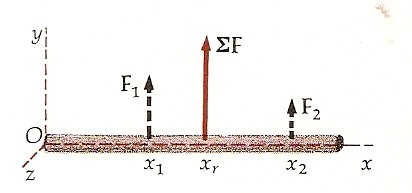
Perché quest’unica forza abbia lo stesso effetto sulla rotazione, si deve scegliere il punto di applicazione in modo che il momento della forza che essa esercita rispetto a qualunque punto sia uguale alla somma dei momenti esercitati dalle due forze iniziali. Siano x1 ed x2 i bracci delle forze iniziali rispetto al punto O. La forza risultante Σ F produrrà lo stesso momento rispetto a O se è applicata a una distanza data da:

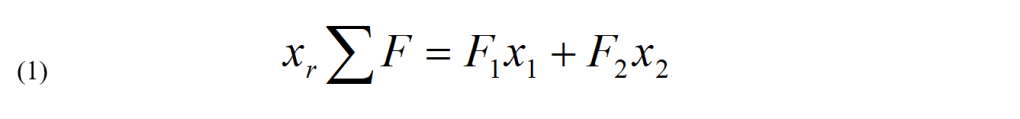
Si può usare questo risultato per dimostrare che la forza di gravità esercitata sulle varie parti di un corpo può essere sostituita con un’unica forza, il peso totale, agente nel centro di massa. La figura seguente rappresenta un corpo costituito da parecchie piccole particelle, ciascuna di peso wi. Il totale è W = Σ wi.

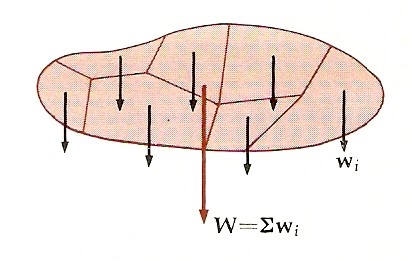
Generalizzando l’equazione (1) al caso di più forze concordi e usando la relazione Σ F = W, si ha, per il punto di applicazione xg della forza risultante:

Di solito il baricentro coincide con il centro di massa.

Se due forze sono parallele e discordi, non si può sostituirle con un’unica forza che abbia lo stesso effetto. Due forze uguali e contrarie agenti com’è indicato nella figura costituiscono una coppia.

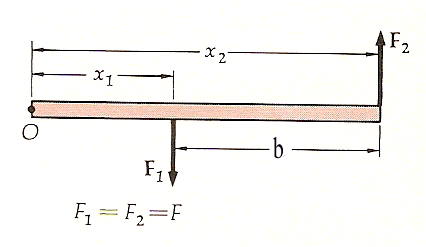
Il momento prodotto da queste forze rispetto al punto O è:

dove F è il modulo di ciascuna forza e b = x2 – xl è la distanza fra di esse. Questo risultato non dipende dalla scelta del punto O e il momento prodotto da una coppia è lo stesso rispetto a tutti i punti dello spazio.

Le due forze parallele e discordi, di moduli disuguali, della figura seguente possono essere sostituite con un’unica forza uguale alla forza risultante e una coppia, com’è illustrato nella figura.

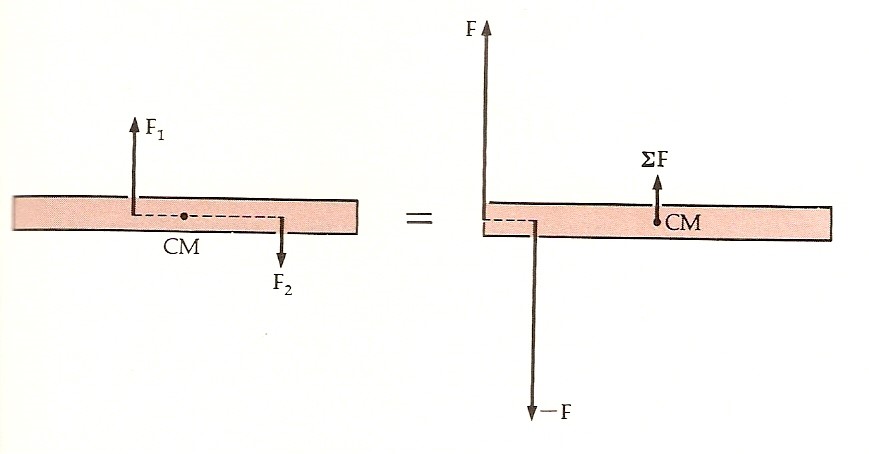
[Con CM si è indicato il centro di massa o baricentro]

In generale, qualunque numero di forze parallele concordi e discordi può essere sostituito con un’unica forza risultante e una coppia. Poiché la forza risultante esercitata da una coppia è nulla, la coppia può essere equilibrata soltanto da una seconda coppia che eserciti un momento uguale e contrario.

7 – Teorema di Koenig

Sia G il baricentro di un sistema di punti in moto rispetto ad un sistema inerziale e sia v la velocità di G rispetto a tale riferimento. Si indichi con vi la velocità di un generico punto Pi del sistema- Si consideri ora una terna di riferimento con l’origine in G e gli assi orientati verso direzioni fisse. Detta wi la velocità di Pi rispetto a questa terna, dalla cinematica dei moti relativi si ricava:

Sostituendo nella relazione (2) il valore di vi dato dalla (1), si ha:

:Analizziamo separatamente il valore dei tre termini che compaiono sotto la sommatoria:-

          Il primo è:

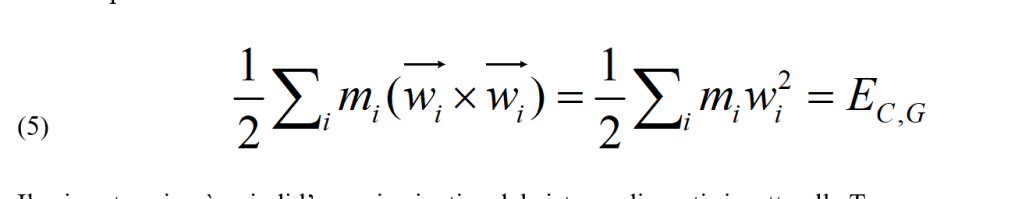
Il primo termine è quindi l’energia cinetica del sistema di punti rispetto alla Terra con origine nel baricentro.

Il secondo termine si può scrivere:

E quindi l’intero secondo termine è nullo.

          Il terzo termine si può scrivere

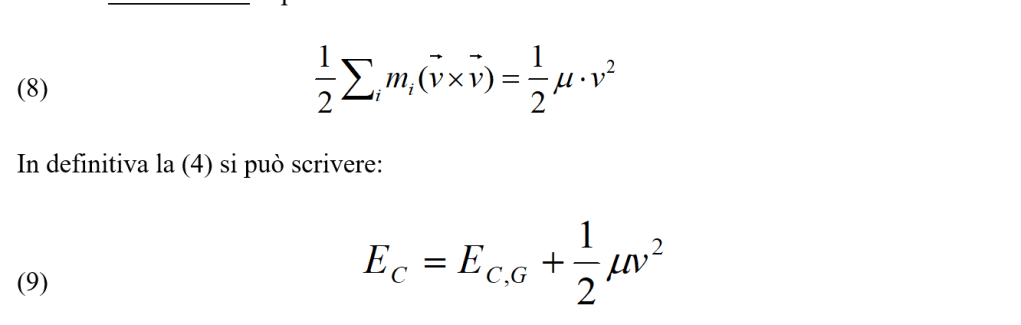
Osserviamo che Σ mi = μ è la massa totale del sistema e che Σ wi dovrebbe essere la velocità vg del baricentro. Ma le wi sono riferite al baricentro che coincide con l’origine del sistema di riferimento e quindi, in tale sistema, vg = 0. Ciò vuol dire che

Si ha in definitiva il Teorema di Koenig:

L’energia cinetica di un sistema in moto è uguale all’energia cinetica che esso possiede rispetto ad un sistema di riferimento baricentrico (di orientamento costante), aumentata dall’energia cinetica che avrebbe un punto che si muovesse con la velocità del baricentro e nel quale fosse concentrata tutta la massa del sistema.

Categorie:Senza categoria